ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
Факультет «Финансы и кредит»
КОНТРОЛЬНАЯ РАБОТА
ПО ФИНАНСОВОЙ МАТЕМЕТИКЕ
Вариант 4
Москва 2007
|
Задача
1
|
|
|
|
|
|
|
|
|
Даны поквартальные данные о кредитах от коммерческого
банка на жилищное строительство ( в условных единицах) за 4 года
|
|
|
Строка соответствует году, столбец - кварталу
|
|
|
|
|
|
|
|
|
|
|
|
|
1-кв.
|
2-кв.
|
3-кв.
|
4-кв.
|
|
|
|
|
1-й год
|
36,0
|
46,0
|
56,0
|
34,0
|
|
|
|
|
2-й год
|
39,0
|
50,0
|
59,0
|
37,0
|
|
|
|
|
3-й год
|
44,0
|
54,0
|
65,0
|
40,0
|
|
|
|
|
4-й год
|
0,0
|
0,0
|
0,0
|
0,0
|
|
|
|
|
Требуется:
|
|
|
1) Построить адапртивную мультипликативную модель
Хольста-Уинтерса с учетом сезонного фактора, приняв параметры сглаживания:
|
|
|
Параметры сглаживания
|
|
|
|
альфа1
|
альфа2
|
альфа3
|
|
|
Значения параметров
|
|
|
|
0,3
|
0,6
|
0,3
|
|
|
2)Оценить точность построенноей модели с использованием
средней относительной ошибки апроксимации.
|
|
|
3)Оценить адексатность построенной модели на основе
исследования:
|
|
|
случайной компоненты по критерию пиков
|
|
|
независимости уровней ряда остатков по d-критерию
(критические значения d1=1,10 и d2=1,37) и по первому коэффициенту
автокорреляции при критическом значении r1=0,32
|
|
|
нормальности распределения остаточной компоненты по
R/S-критерию с критическими значениями от 3 до 4,21
|
|
|
4) Построить точечный прогноз на 4 шага вперед, т.е. на 1
год
|
|
|
5) Отразить на графике фактические, расчетные и прогнозные
данные.
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
|
|
|
1)Построение
адаптивной мультипликативной
модели Хольта-Уинтерса
|
|
|
|
Для оценки нач. значений a(0) и b(0) применим линейную
модель к первым 8 значения ряда
|
|
|
|
Линейная модель
имеет вид
|
|
|
|
|
|
|
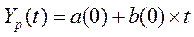
|
|
|
|
|
(1.0)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Метод
наименьших квадратов дает возможность определить коэффициенты линейного
|
|
|
уравнения 1.0. по формулам 1.1-.1.4 :
|
|
|
|
|
|
|
|
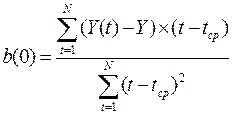
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.1)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
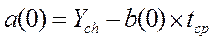
|
|
|
|
|
|
|
|
|
(1.2)
|
|
|
|
|
|
|
|
|
|
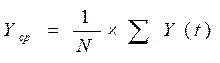 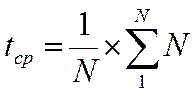
|
|
|
(1.3)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.4)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Использованные
для расчета первые 8 членов ряда приведены ниже
|
|
|
t
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
Y(t)
|
33,0
|
42,0
|
50,0
|
33,0
|
36,0
|
46,0
|
56,0
|
34,0
|
|
|
|
|
|
|
|
|
|
|
Промежуточные
вычисления значений переменных и математических выражений,
|
|
|
необходимых
для расчетов по формулам 1.1-1.4 приведены в табл. 1.1
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1.1 Промежуточные вычисления, необходимые
для оценки параметров модели
|
|
t
|
Факт
|
Отклон
|
(t-tср)^2
|
Y(t)-Yср
|
(t-tср)*
|
Расч
|
|
|
|
|
Y(t)
|
t-tср
|
|
|
(Y(t)-Yср)
|
Yp(t)
|
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
|
|
1
|
33,0
|
-3,50
|
12,25
|
-8,25
|
28,88
|
38,42
|
|
|
|
2
|
42,0
|
-2,50
|
6,25
|
0,75
|
-1,88
|
39,23
|
|
|
|
3
|
50,0
|
-1,50
|
2,25
|
8,75
|
-13,13
|
40,04
|
|
|
|
4
|
33,0
|
-0,50
|
0,25
|
-8,25
|
4,13
|
40,85
|
|
|
|
5
|
36,0
|
0,50
|
0,25
|
-5,25
|
-2,63
|
41,65
|
|
|
|
6
|
46,0
|
1,50
|
2,25
|
4,75
|
7,13
|
42,46
|
|
|
|
7
|
56,0
|
2,50
|
6,25
|
14,75
|
36,88
|
43,27
|
|
|
|
8
|
34,0
|
3,50
|
12,25
|
-7,25
|
-25,38
|
44,08
|
|
|
|
36
|
330,0
|
0
|
42,00
|
0,0
|
34,00
|
330,00
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tср.=
|
4,5
|
|
|
|
|
|
|
|
Ycp=
|
41,25
|
|
|
|
|
|
|
Зная
tcp и Ycp рассчитываем графы 3-6 табл.
1.1 , а затем , используя значения
|
|
итоговой строки столбцов 4 и 6
|
|
|
|
|
|
|
по
формулам 1.1 и 1.2 находим
|
|
|
|
|
|
|
a=
|
37,607
|
|
|
|
|
|
|
|
|
b=
|
0,8095
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Затем
по формуле 1.0
|
рассчитываем
значения Yр(t) и заносим в столбец 7
табл.1.1
|
|
|
|
|
|
|
|
|
|
|
Оценим
значения коэффициентов сезонности,
используя данные табл. 1.1
|
|
|
F(-3)=0,5*[
Y(1)/Yp(1) + Y(5)/Yp(5) ] =
|
0,862
|
|
|
|
|
|
F(-2)=0,5*[
Y(2)/Yp(2) + Y(6)/Yp(6) ] =
|
1,077
|
|
|
|
|
|
F(-1)=0,5*[
Y(3)/Yp(3) + Y(7)/Yp(7) ] =
|
1,272
|
|
|
|
|
|
F(0)=0,5*[
Y(4)/Yp(4) + Y(8)/Yp(8) ] =
|
0,789
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Зная a(0), b(0) , параметры
сглаживания и коэффициенты сезонности рассчитаем
|
|
параметры
модели на момент t=1
|
|
|
|
|
|
|
Уравнение
Yp(t) = [a(t-1)+1*b(t-1)] * F(t-L) для t=1
|
|
Yp(1) =33,10
|
|
|
Уравнение
a(t) = альфа1*Y(t)/F(t-L) + (1-альфа1) * [a(t-1)+b(t-1)] для t=1 примет вид
|
|
a(1)=альфа1*Y(1)/F(-3)+(1-альфа1)*{a(0)+b(0)}
=
|
38,39
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение
b(t) = альфа3*[a(t)-a(t-1)] + (1 - альфа3)*b(t-1) для t=1 примет вид
|
|
|
b(1)=альфа3*[a(1) - a(0)] + (1 - альфа3) * b(0) =
|
0,8
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение
F(t) = альфа2*Y(t)/a(t) + (1-альфа2)*F(t-L)
для t=1 примет вид
|
|
|
F(1)= альфа2*Y(1)/a(1) + (1-альфа2)*F(-3) =
|
0,86
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определив
для t=1 значения Y(1), a(1), b(1), F(1) по приведенному выше алгоритму
|
|
определим
эти значения для t= 2, 3, ... , 16. Результаты сведем в табл. 1.2
|
|
|
|
|
|
|
|
|
|
|
|
Tаблица
1.2. Построение модели Хольта-Уинтерса
|
|
|
|
|
t
|
Y(t)
|
a(t)
|
b(t)
|
F(t)
|
Yp(t)
|
Абс.погр.
|
Отн.погр.
|
|
|
|
|
|
|
|
|
E(t)
|
в
%
|
|
|
0
|
|
37,607
|
0,8095
|
0,789
|
|
|
|
|
|
1
|
33
|
38,38
|
0,799
|
0,860
|
33,10
|
-0,10
|
0,30
|
|
|
2
|
42
|
39,13
|
0,783
|
1,075
|
42,19
|
-0,20
|
0,47
|
|
|
3
|
50
|
39,73
|
0,730
|
1,264
|
50,74
|
-0,74
|
1,48
|
|
|
4
|
33
|
40,86
|
0,850
|
0,800
|
31,95
|
1,05
|
3,18
|
|
|
5
|
36
|
41,75
|
0,861
|
0,862
|
35,89
|
0,11
|
0,29
|
|
|
6
|
46
|
45,67
|
0,878
|
1,077
|
45,80
|
0,20
|
0,43
|
|
|
7
|
56
|
43,78
|
0,947
|
1,273
|
55,02
|
0,98
|
1,74
|
|
|
8
|
34
|
44,05
|
0,745
|
0,783
|
35,80
|
-1,80
|
5,28
|
|
|
9
|
39
|
44,94
|
0,788
|
0,865
|
38,59
|
0,41
|
1,04
|
|
|
10
|
50
|
45,94
|
0,851
|
1,084
|
49,24
|
0,76
|
1,53
|
|
|
11
|
59
|
46,66
|
0,812
|
1,268
|
59,56
|
-0,56
|
0,95
|
|
|
12
|
37
|
47,40
|
0,791
|
0,782
|
37,18
|
-0,18
|
0,49
|
|
|
13
|
44
|
48,99
|
1,030
|
0,885
|
41,70
|
2,30
|
5,22
|
|
|
14
|
54
|
49,96
|
1,013
|
1,082
|
54,21
|
-0,21
|
0,39
|
|
|
15
|
65
|
51,06
|
1,039
|
1,271
|
64,63
|
0,37
|
0,57
|
|
|
16
|
40
|
51,82
|
0,955
|
0,776
|
40,72
|
-0,72
|
1,81
|
|
|
|
|
|
|
|
|
|
|
|
a1=
|
0,3
|
|
|
|
|
|
|
|
|
a2=
|
0,6
|
|
|
|
|
|
|
|
|
a3=
|
0,3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 .
ПРОВЕРКА АДЕКВАТНОСТИ
|
|
|
|
|
|
|
Для того, чтобы модель была адекватна
исследуемому процессу ряд остатков
E(t) должен
|
|
|
обладать
свойствами а) случайности, б)
независимости последовательных уровней и
|
|
|
в)
нормальности распределения
|
|
|
|
|
|
|
Для
оценки адекватности модели проводим промежуточные расчеты (см.табл.1.3)
|
|
|
В
гр.2 внесены фактические значения Y(t), а в гр.3 их отклонение от расчетных
значений Yp(t)
|
|
|
|
|
|
|
|
|
|
|
|
Таблица
1.3 Промежуточные расчеты для оценки адекватности модели
|
|
|
|
t
|
Факт
|
Отклон
|
Точки
|
e(t)^2
|
e(t-1)
|
[e(t)*e(t-1)]^2
|
e(t)*e(t-1)
|
|
|
Y(t)
|
E(t)
|
поворота
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
1
|
33
|
-0,10
|
хххх
|
0,01
|
|
|
|
|
2
|
42
|
-0,20
|
0
|
0,04
|
-0,10
|
0,01
|
0,0197
|
|
3
|
50
|
-0,74
|
1
|
0,55
|
-0,20
|
0,29
|
0,1458
|
|
4
|
33
|
1,05
|
1
|
1,10
|
-0,74
|
3,20
|
-0,7770
|
|
5
|
36
|
0,11
|
1
|
0,01
|
1,05
|
0,90
|
0,1113
|
|
6
|
46
|
0,20
|
0
|
0,04
|
0,11
|
0,01
|
0,0212
|
|
7
|
56
|
0,98
|
1
|
0,95
|
0,20
|
0,61
|
0,1954
|
|
8
|
34
|
-1,80
|
1
|
3,22
|
0,98
|
7,73
|
-1,7537
|
|
9
|
39
|
0,41
|
0
|
0,16
|
-1,80
|
4,84
|
-0,7277
|
|
10
|
50
|
0,76
|
1
|
0,58
|
0,41
|
0,13
|
0,3093
|
|
11
|
59
|
-0,56
|
1
|
0,31
|
0,76
|
1,74
|
-0,4280
|
|
12
|
37
|
-0,18
|
0
|
0,03
|
-0,56
|
0,14
|
0,1008
|
|
13
|
44
|
2,30
|
1
|
5,28
|
-0,18
|
6,15
|
-0,4130
|
|
14
|
54
|
-0,21
|
1
|
0,04
|
2,30
|
6,30
|
-0,4780
|
|
15
|
65
|
0,37
|
1
|
0,14
|
-0,21
|
0,58
|
-0,0771
|
|
16
|
40
|
-0,72
|
хххх
|
0,52
|
0,37
|
1,19
|
-0,2682
|
|
136
|
718
|
2
|
10
|
13,01
|
|
33,58
|
-4,02
|
|
Количество
точек поворота p =
|
10
|
|
|
|
|
|
2.1.Проверка
случайности уровней на основе критерия поворотных точек
|
|
|
критерия
поворотных точек. Для этого каждый уровень ряда сравниваем с двумя соседними.
|
|
|
Если он
больше (либо меньше) обеих соседних уровней , то он является поворотной
точкой
|
|
|
и тогда
в столбце 4 рядом с ним ставим 1. В
первой и последней строку ставим
прочерки т.к. у
|
|
этих
уровней нет двух соседних уровней . Общее число поворотных точек равно
|
10
|
|
|
Оно
приведено в последней строке таблицы, Обозначим его через р
|
|
|
|
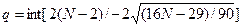
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если
количество поворотных точек p больше q, то условие случайности уровней
выполнено. В нашем случае p=10,q=6 значит условие случайности уровней ряда
остатков выполнено.
|
|
|
|
|
|
|
|
|
|
|
|
2.2.
Проверка НЕЗАВИСИМОСТИ уровней ряда остатков (ОТСУТСТВИЯ АВТОКОРРЕЛЯЦИИ)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проверку
проводим двумя методами :
|
|
|
|
|
|
|
а)
по d-критерию Дарбина-Уотсона ;
|
|
|
|
|
|
|
б)
по первому коэффициенту автокорреляции r(1).
|
|
|
|
|
|
|
|
|
|
|
|
|
Для
проверки по d-критерию Дарбина-Уотсона рассчитали значение d и если полученное
|
|
|
значение
больше 2 то находим уточненное значение равное 4-d
|
|
|
|
|
|
|
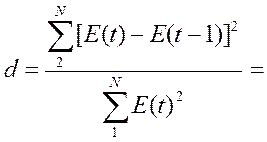
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,58
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значение dw статистики близко к величине 2(1-r(1))
Соответственно, идеальное
значение статистики - 2 (автокорреляция отсутствует). Меньшие значения критерия соответствуют
положительной автокорреляции остатков, большие значения - отрицательной.
При сравнении расчетного значения
dw статистики с табличным могут возникнуть такие ситуации:
d2 < dw < 2 –уровни ряда остатков являются
независимыми ;
dw < d1 – остатки содержат
автокорреляцию;
d1 < dw < d2 – область неопределенности,
когда нет оснований ни принять,
ни отвергнуть гипотезу о существовании автокорреляции.
Если d > 2, то это свидетельствует о
наличии отрицательной корреляции.
Перед сравнением с табличными
значениями dw
критерий следует преобразовать по
формуле dw´=4 – dw =4-2,58=1,42
Табличное значение d1=1,10 d2=1,37 для n=16
1,10 < 1,42 <2 – уровни
ряда остатков являются независимыми
Проверка по первому коэффициенту автокорреляции r(1)
Первый
коэффициент автокорреляции
Из условия задачи критическ. r=0,32
В
зависимости от соотношения между расчетной величиной r(1) и r критическим
находим/
Если модуль рассчитанного значения
меньше критического значения, то уровни ряда остатков независимы.
-0,31<0.32 – значит уровни
независимы.
В этом случае гипотеза
принимается и модель считается адекватной процессу.
3. Соответствие ряда остатков
нормальному закону распределения проверим с помощью R/S-критерия.
Согласно общим предположениям
регрессионного анализа остатки должны вести себя как независимые одинаково
распределенные случайные величины (нормальный закон распределения)
по формуле:
- максимальный и минимальный уровни ряда
остатков соответственно;

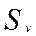
-
стандартное отклонение
Если расчетное значение попадает
между табулированными границами с заданным уровнем вероятности, то гипотеза о
нормальном распределении ряда остатков принимается.
Вариационный размах составляет 2,30 и среднеквадратическое
отклонение -1,8
По этим данным рассчитаем
критерий R/S = 4,4
Для n=16 и а=0,05 найдем
критический интервал: (3,00; 4,21)
Вычисленное значение 4,56 не попадает между табулированными границами с
заданным уровнем вероятности.
Значит, закон нормального
распределения не выполняется.
4. Оценим точность построенной
модели
Средняя по модулю относительная
погрешность рассчитывалась из соотношения
Также для оценки точности регрессионных
моделей целесообразно использовать среднюю относительную ошибку аппроксимации:
В среднем расчетные значения
ŷ для линейной модели отличаются от фактических значений на 1,57%.
Чем меньше рассеяние эмпирических точек вокруг
теоретической линии регрессии, тем
меньше средняя ошибка аппроксимации.
Ошибка аппроксимации меньше 5 %
свидетельствует о хорошем качестве модели.
5. Составим точечный прогноз на 1 год
вперед с t=17 по t=20
Прогнозные значения на k шагов вперед рассчитываем
по формуле
Yp(t+k)= [ a(t) + k*b(t) ] * F(t - 4 + k) для t=16
Yp(16+k)=[a(16)+k*b(16)] * F(16 - 4 + k)
Yp(17)=[ a(16)+1*b(16)]*F(16- 4 + 1)
Yp(18)= [a(16)+2*b(16)]*F(16 -4 +2)
Yp(19)= [ a(16)+3*b(16)]*F(16-4+3)
Yp(20)=[a(16)+4*b(16) *F(16-4+4)
|
Время
|
Факт.
|
Расчет
|
|
1
|
33,0
|
33,10
|
|
2
|
42,0
|
42,20
|
|
3
|
50,0
|
50,74
|
|
4
|
33,0
|
31,95
|
|
5
|
36,0
|
35,90
|
|
6
|
46,0
|
45,80
|
|
7
|
56,0
|
55,02
|
|
8
|
34,0
|
35,80
|
|
9
|
39,0
|
38,60
|
|
10
|
50,0
|
49,24
|
|
11
|
59,0
|
59,56
|
|
12
|
37,0
|
37,18
|
|
13
|
44,0
|
41,70
|
|
14
|
54,0
|
54,21
|
|
15
|
65,0
|
64,63
|
|
16
|
40,0
|
40,72
|
|
17
|
|
46,7
|
|
18
|
|
58,1
|
|
19
|
|
69,5
|
|
20
|
|
43,2
|
|
|
|
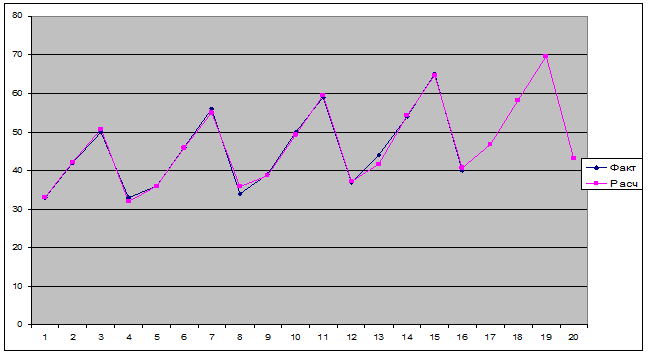
На
нижеприведенном рисунке проводиться сопоставление фактических и расчетных
данных. Здесь же показаны и прогнозные значения цены акции на 1 год
вперед. Из рисунка видно, что расчетные
данные хорошо согласуются с фактическими, что говорит об удовлетворительном
качестве прогноза.
Задача 2
|
Даны
цены (открытия,максимальная, минимальная и закрытия) за 10 дней.
|
|
Дни t
|
Макси-мальная
цена за день Н(t)
|
Мини-мальная
цена за день L(t)
|
Цена
закрытия, С(t)
|
|
|
|
|
|
1
|
2
|
3
|
4
|
|
|
|
|
|
1
|
744
|
705
|
709
|
|
|
|
|
|
2
|
743
|
675
|
738
|
|
|
|
|
|
3
|
750
|
700
|
735
|
|
|
|
|
|
4
|
759
|
707
|
751
|
|
|
|
|
|
5
|
770
|
740
|
755
|
|
|
|
|
|
6
|
776
|
661
|
765
|
|
|
|
|
|
7
|
756
|
715
|
720
|
|
|
|
|
|
8
|
745
|
685
|
739
|
|
|
|
|
|
9
|
758
|
725
|
740
|
|
|
|
|
|
10
|
730
|
673
|
678
|
|
|
|
|
|
Интервал сглаживания принять равным
|
5
|
дням. Рассчитать
|
|
|
Решение
|
|
|
|
|
|
|
|
|
|
Интервал сглаживания равен
|
5
|
дням
|
|
|
|
|
|
Находим
коэффициент k
|
k=2/(5+1) =
|
0,333333
|
|
|
|
|
|
Находим
простую среднюю за 5 дней и это
значение
|
737,6
|
|
|
|
|
используем
в качестве
|
начального
значения экспоненциальной скользящей средней
|
|
Дальнейшие
значения рассчитываем по формуле
|
ЕМА(t) = C(t)*k+EMA(t-1)*(1-k)
|
|
|
|
|
|
|
|
|
|
|
|
|
Расчеты
приведены в таблице 2а
|
|
|
|
|
|
|
Таблица 2а
|
|
|
|
|
|
|
|
|
|
Дни,
t
|
Цена
закры-тия , C(t)
|
Экспонен-циальная
скользя-щая средняя, EMA(t)
|
|
|
|
|
|
|
|
|
1
|
2
|
4
|
|
|
|
|
|
|
|
|
1
|
709
|
|
|
|
|
|
|
|
|
|
2
|
738
|
|
|
|
|
|
|
|
|
|
3
|
735
|
|
|
|
|
|
|
|
|
|
4
|
751
|
|
|
|
|
|
|
|
|
|
5
|
755
|
737,6
|
|
|
|
|
|
|
|
|
6
|
765
|
746,7
|
|
|
|
|
|
|
|
|
7
|
720
|
737,737,8
|
|
|
|
|
|
|
|
|
8
|
739
|
738,2
|
|
|
|
|
|
|
|
|
9
|
740
|
738,8
|
|
|
|
|
|
|
|
|
10
|
678
|
718,5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2б) момент и скорость
изменения цен
|
|
|
|
|
|
|
|
Решение
|
|
|
|
|
|
|
|
|
|
|
|
Момент
|
MOM(t)=C(t)
- C(t-n+1), где
|
C(i)
- цена закрытия i-го дня
|
|
|
|
|
|
|
В
графу 3 для t=5 вносим разность значений из графы 2: С(5)-С(1)
|
|
|
|
для t=6 в графу 3 вносят С(6)-С(2) и т.д.
|
|
|
|
|
|
|
|
Аналогично
рассчитывают скорость изменения цен по ф-ле
|
ROC(t)=
|
[C(t) / C(t-n+1)] * 100%
|
|
|
Расчеты
приведены в таблице 2б
|
|
|
|
|
|
|
|
|
Таблица 2б.
Расчет Мomtntum, ROC
|
|
|
Дни,
t
|
Цены
закры-тия, C(t)
|
Momtntum,
MOM(t)
|
ROC(t)
|
|
|
|
1
|
2
|
3
|
4
|
|
|
|
1
|
709
|
|
|
|
|
|
2
|
738
|
|
|
|
|
|
3
|
735
|
|
|
|
|
|
4
|
751
|
|
|
|
|
|
5
|
755
|
46
|
106,5
|
|
|
|
6
|
765
|
27
|
103,7
|
|
|
|
7
|
720
|
-15
|
98,0
|
|
|
|
8
|
739
|
-12
|
98,4
|
|
|
|
9
|
740
|
-15
|
98,0
|
|
|
|
10
|
678
|
-87
|
88,6
|
|
|
|
2в) индекс
относительной силы RSI
|
|
|
|
|
|
|
|
|
|
Решение
|
|
|
|
|
|
|
|
|
|
|
|
|
|
RSI(t) = 100 - 100 / [1+AU(t) / AD(t) ] где
AU и AD сумма приростов и убыли конечных цен за n дней, включая
текущий
|
|
Начиная со 2 дня до конца табл,
абс.значение разности между текущей ценой и ценой предыдущего дня
записываем
|
|
в
графу 3 (если цена возросла) или в графу 4 (если цена понизилась) .
|
|
|
|
|
|
|
|
Начиная с шестого дня до конца таблицы в
графу 5, содержащую сумму повышений цен AU(t),вносим сумму
|
|
|
приростов
цен из графы 3 за 5 последних дней
(включая текущий).Эту сумму определяем
сложением значений
|
|
|
графы
3 за 5 последних дней (включая
текущий). Для t=6 это будет
суммирование значений графы 3 со 2-го
дня
|
|
|
по
6-ой включительно, для t=7это будут
суммироваться значения графы 3 с 3-го дня по 7-й и т.д. до конца таблицы
|
|
Аналогично
заполняем графу 6, внося в нее сумму значений из графы 4 за последние 5 дней
(включая текущий).
|
|
|
Рассчитываем RSI(t) = 100 - 100 / [1+AU(t) / AD(t) ] где
AU(t) и AD(t) берем из 6-й и 7-й графы таблицы.
|
|
|
|
Резултаты
записываем в графу 8 таблицы 2в.
|
|
|
|
|
|
|
|
|
Таблица 2в.
Расчет RSI
|
|
|
|
|
|
|
|
|
|
|
|
Дни,
t
|
Цены
закры-тия, C(t)
|
Повышение
цены за день
|
Понижение
цены за день
|
Сумма
повышений, AU(t)
|
Сумма
понижений, AD(t)
|
RSI
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
|
1
|
709
|
|
|
|
|
|
|
|
2
|
738
|
29
|
0
|
|
|
|
|
|
3
|
735
|
0
|
3
|
|
|
|
|
|
4
|
751
|
16
|
0
|
|
|
|
|
|
5
|
755
|
4
|
0
|
|
|
|
|
|
6
|
765
|
10
|
0
|
59
|
3
|
95,2
|
|
|
7
|
720
|
0
|
45
|
30
|
48
|
38,5
|
|
|
8
|
739
|
19
|
0
|
49
|
45
|
52,1
|
|
|
9
|
740
|
1
|
0
|
34
|
45
|
43,0
|
|
|
10
|
678
|
0
|
62
|
30
|
107
|
21,9
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2г) Расчет %K, %R, %D
|
|
|
|
|
|
|
|
|
|
|
|
Индикатор %К(t) =100*[C(t)
- L(5)] / [H(5) - L(5)]
|
|
|
|
|
|
|
|
|
|
где L(5) и
H(5) минимальная и максимальная цены за предшествующек 5 дней, включая
текущий t (графы 5 и 6)
|
|
|
Индикатор %R(t) =100*[H(t)
- C(t)] / [H(5) - L(5)]
|
|
|
|
|
|
|
|
|
|
где L(5) и
H(5) минимальная и максимальная цены за предшествующек 5 дней, включая
текущий t (гр.5 и 6)
|
|
|
При расчете %K(t) и %D(t)
для t-го дня необходимо знать минимальное и максимальное
|
|
|
значения цен за 5
предшествующих дней, включая текущий т.е с (t-4)-го дня по текущий день t.
|
|
|
|
|
Максимальная цена за 5 дней
- Н(5) находится с помошью функции МАКС( ) в графе 2,
|
|
|
содержащей максимальные
цены за каждый день, и заносится с графу 5.
|
|
|
|
|
|
|
Минимальная цена за 5 дней
- L(5) находится с помошью функции МИН( ) в графе 3,
|
|
|
|
содержащей минимальные цены
за каждый день, и заносится с графу 6.
|
|
|
|
|
|
|
|
Результаты промежуточных
расчетов значений C(t)-L(5), H(5)-C(t), H(5)-L(5) заносятся в графы 7-9
|
|
По приведенным выше
формулам рассчитываются значения %K, %R и разультаты заносятся
|
|
в графы10 и 11
|
|
|
|
|
|
|
|
|
|
|
|
|
Начиная с 7-го дня до конца таблицы в
графу 12вносим сумму значений графы 7 за 3
последних дней (включая
|
|
|
текущий). Для t=7 это будет суммирование значений графы 7 с 5-го дня по 7-й день. Для t=8
это будет суммирование
|
|
значений графы 7 с 6-го дня по 8-й день и т.д до
конца таблицы. Графу 13 заполняем аналогично, суммируя значения
|
|
из графы 9. Индикатор %D(t)
=100*Cумма[C(t) - L(5) ] / Сумма[H(5) - L(5)] где Cумма[C(t) - L(5) берется
из графы 12,
|
|
|
а Сумма[H(5) - L(5)] из
графы 13. Результаты расчетов сведены в графу 14 таблицы.2г.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2г.
Расчет %K, %R, %D
|
|
|
|
|
|
|
|
|
|
|
Дни t
|
Макси-мальная
цена за день Н(t)
|
Мини-мальная
цена за день L(t)
|
Цена
закрытия, С(t)
|
Макси-мальная
цена за 5 дней ,Н(5)
|
Мини-мальная
цена за 5 дней, L(5)
|
Гр.4
минус Гр.6 C(t)-L(5)
|
Гр.5
минус Гр.4 H(5)-C(t)
|
Гр.5
минус Гр.6 Н(5)-L(5)
|
(Гр.7 / Гр.9 )
* 100% %K
|
(Гр.8 / Гр.9 )
* 100% %R
|
Сумма
за 3 дня Гр.7
|
Сумма
за 3 дня Гр.8
|
(Гр.12
/Гр.13 ) * 100% %D
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
|
1
|
744
|
705
|
709
|
|
|
|
|
|
|
|
|
|
|
|
2
|
743
|
675
|
738
|
|
|
|
|
|
|
|
|
|
|
|
3
|
750
|
700
|
735
|
|
|
|
|
|
|
|
|
|
|
|
4
|
759
|
707
|
751
|
|
|
|
|
|
|
|
|
|
|
|
5
|
770
|
740
|
755
|
770
|
675
|
80
|
15
|
95
|
84,21
|
15,79
|
|
|
|
|
6
|
776
|
661
|
765
|
776
|
661
|
104
|
11
|
115
|
90,43
|
9,57
|
|
|
|
|
7
|
756
|
715
|
720
|
776
|
661
|
59
|
56
|
115
|
51,30
|
48,70
|
243
|
325
|
74,77
|
|
8
|
745
|
685
|
739
|
776
|
661
|
78
|
37
|
115
|
67,83
|
32,17
|
241
|
345
|
69,86
|
|
9
|
758
|
725
|
740
|
776
|
661
|
79
|
36
|
115
|
68,70
|
31,30
|
216
|
345
|
62,61
|
|
10
|
730
|
673
|
678
|
776
|
661
|
17
|
98
|
115
|
14,78
|
85,22
|
174
|
345
|
50,43
|
Задача 3
|
|
Дата начальная
|
Дата конечная
|
Время в днях
|
Время в годах
|
ставка %
|
Число
начислений
|
|
Сумма
|
Tн
|
Тк
|
Тдн
|
Тлет
|
ставка %
|
m
|
|
2 000 000,00р.
|
16.01.2002
|
14.03.2002
|
180
|
4,00
|
25,00
|
2,00
|
|
Банк
выдал ссуду, размером Р руб. Дата
выдачи ссуды - Тн, возврата – Тк. День
выдачи и день
|
|
возврата
считать за 1 день. Проценты рассчитываются
по простой процентной ставке i % годовых. Найти:
|
|
а)
точные проценты с точным числом дней ссуды ;
|
|
|
|
|
б)
обыкновенные проценты с точным числом дней ссуды
|
|
|
|
|
в)
обыкновенные проценты с приближенным числом дней ссу-ды
|
|
|
|
Решение
|
|
|
|
|
|
|
|
Точное
число дней ссуды =
|
57,00
|
|
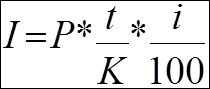
|
|
|
|
Приблизительное
число дней ссуды равно
|
|
|
|
|
|
в
январе
|
15
|
|
|
|
|
|
|
в
феврале
|
30
|
|
|
|
|
|
|
в
марте
|
14
|
|
|
|
|
|
|
Итого
|
59
|
|
|
|
|
|
|
Считая
день выдачи и день возврата за 1 день, приблизительное число дней равно
|
58,00
|
|
Точное
число дней в 2002 г
=
|
365
|
Приближенное число дней в любом году =
|
360,00
|
|
а)
Найдем точные проценты с точным числом дней ссуды
|
|
|
ссуда Р
|
t
|
K
|
ставка i%
|
Проценты
|
|
2 000 000,00р.
|
57,00
|
365
|
25,00
|
78 082,19р.
|
|
б)
Найдем обыкновенные проценты с точным числом дней ссуды ;
|
|
ссуда Р
|
t
|
K
|
ставка i%
|
Проценты
|
|
2 000 000,00р.
|
57,00
|
360,00
|
25,00
|
79 166,67р.
|
|
в)Найдем
обыкновенные проценты с приближенным числом дней ссу-ды
|
|
ссуда Р
|
t
|
K
|
ставка i%
|
Проценты
|
|
2 000 000,00р.
|
58,00
|
360,00
|
25,00
|
80 555,56р.
|
|
Через
Тдн после подписания договора, должник уплатит S рублей. Кредит выдан
|
|
|
|
под i % годовых. Какова первоначальная сумма
долга и дисконт (проценты обычные)?
|
|
|
|
S
|
t
|
ставка i%
|
K
|
|
|
|
2 000 000,00р.
|
180
|
25,00
|
360,00
|
|
|
|
Решение. Используем
формулы
|
|
|
|
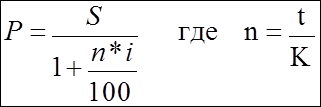
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
первоначальная сумма долга равна
|
1 777 777,78р.
|
|
|
Дисконт
= P-S=
|
222 222,22р.
|
|
|
|
|
Задача 3.3
|
|
|
|
|
|
|
Через Тдн предприятие должно получить по
векселю S рублей. Банк приобрел
|
|
этот
вексель с дисконтом. Банк учел вексель
по учетной ставке d % годовых
|
|
(год равен 360 дням). Определить полученную
предприятием сумму и дисконт.
|
|
S
|
t
|
ставка %
|
K
|
|
2 000 000,00р.
|
180
|
25,00
|
360,00
|
|
Решение. Используем
формулы
|
|
|
|
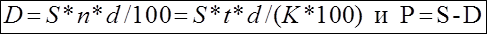
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дисконт
равен
|
250 000,00р.
|
|
|
|
|
Полученная
предприятием сумма равна
|
1 750 000,00р.
|
|
|
В
кредитном договоре, на сумму Р руб и сроком
на Тлет, зафиксирована ставка
сложных
|
|
процентов, равная i% годовых. Определить наращеную сумму.
|
|
P
|
n
|
ставка %
|
|
|
|
2
000 000,00р.
|
4,00
|
25,00
|
|
|
|
Решение. Используем
формулу
|
|
|
|
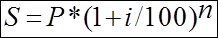
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определим наращеную сумму. S=
|
4 882 812,50р.
|
|
|
Задача 3.5
|
|
|
|
|
|
|
|
Ссуда
размером Р руб. предоставлена на Т лет. Проценты сложные, ставка равна
i % годовых
|
|
Проценты
начисляются m раз в году. Вычислить наращенную сумму.
|
|
|
|
P
|
n
|
ставка %
|
m
|
|
2
000 000,00р.
|
4,00
|
25,00
|
2,00
|
|
Решение. Используем
формулу
|
|
|
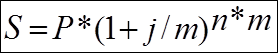
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определим наращеную сумму. S=
|
5 131 569,03р.
|
|
Задача 3.6
|
|
|
|
|
|
|
Вычислить
эффективную ставку процента, если банк начисляет проценты m раз в году
|
|
,
исходя из номинальной ставки i% годовых.
|
|
|
|
ставка i %
|
m
|
|
|
|
|
|
25,00
|
2,00
|
|
|
|
|
|
Решение. Используем
формулу
|
|
|
|
|
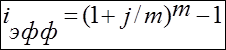
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычислим
(в долях единицы) iэфф =
|
0,2656
|
|
|
|
Чтобы
получить в процентах надо умножить на 100, итого=
|
26,56
|
процентов
|
|
Задача 3.7
|
|
|
|
|
|
|
Определить
какой должна быть номинальная ставка при
начислении процентов m раз в году,
|
|
чтобы обеспечить эффективную ставку i%
годовых.
|
|
|
|
ставка i %
|
m
|
|
|
|
|
|
25,00
|
2,00
|
|
|
|
|
|
Решение. Используем
формулу
|
|
|
|
|
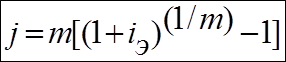
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
номинальная
ставка при начислении процентов m раз
в году равна
|
0,236067977
|
|
Чтобы
получить в процентах надо умножить на 100, итого=
|
23,61
|
|
|
Задача 3.8
|
|
|
|
|
|
|
Через
Тлет лет предприятию будет выплачена сумма
S руб. Определить ее современную стоимость,
|
|
при условии, что применяется ставка сложных процентов i % годовых.
|
|
|
S
|
Тлет
|
ставка
%
|
|
|
|
|
2 000 000,00р.
|
4,00
|
25,00
|
|
|
|
|
Решение. Используем
формулу
|
|
|
|
|
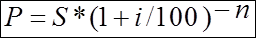
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определим современную стоимость P=
|
819
200,00р.
|
|
|
|
Задача 3.9
|
|
|
|
|
|
|
|
Через
Тлет по вексалю должна быть выплачена сумма
S руб. Банк
|
|
|
|
учел
вексель по сложной учетной ставке i % годовых. Определить дисконт.
|
|
|
|
S
|
Тлет
|
d %
|
|
|
|
|
|
2
000 000,00р.
|
4,00
|
25,00
|
|
|
|
|
|
Решение. Используем
формулы для современной стоимости суммы и дисконта при банковском
учете
|
|
Дисконтирование
по сложной учетной ставке
осуществляется по формуле
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определим современную стоимость суммы Р=
|
632 812,50
|
|
|
|
Дисконт
равен
|
1 367 187,50р.
|
|
|
|
|
|
|
Задача 3.10
|
|
|
|
|
|
|
|
В
течение Т лет на расчетный счет в конце каждого года поступает по S руб.,
|
|
|
на
которые m раз в году начисляются проценты по сложной годовой ставке i%. Определить сумму
|
|
на
расчетном счете к концу указанного срока.
|
|
|
|
|
P
|
n
|
ставка %
|
m
|
|
|
|
|
2
000 000,00р.
|
4,00
|
25,00
|
2,00
|
|
|
|
|
Решение. Используем
формулу
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сумма
на расчетном счете к концу срока будет S=
|
11 789
436,34
|
|
|