ВСЕРОССИЙСКИЙ
ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
Контрольная работа
По дисциплине «Финансовая Математика»
|
Исполнитель:
|
|
|
Специальность
|
|
|
Группа
|
|
|
№ зачетной книжки
|
|
|
Вариант
|
|
|
Руководитель:
|
|
Уфа
2006г.
ЗАДАЧА 1 ЗАДАЧА
1 (ИЗ КОНТГОЛЬНОЙ РАБОТЫ)
Приведены
поквартальные данные о кредитах коммерческого банка, выданных на жилищное
строительство (в у. е.) за 4 года (всего 16 кварталов, первый столбец
соответствует первому кварталу первого года).
|
квартал t
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
|
Y(t)
|
33
|
42
|
50
|
33
|
36
|
46
|
56
|
34
|
39
|
50
|
59
|
37
|
44
|
54
|
65
|
40
|
Требуется
1) Построить адаптивную мультипликативную модель
Хольта-Уинтерса с учетом сезонного фактора, приняв параметры сглаживания a1=0.3, a2=0.6, a3=0.3.
2) Оценить точность построенной модели, вычислив среднюю
относительную ошибку аппроксимации.
3) Проверить адекватность построенной модели на основе
исследования:
- случайности
остаточной компоненты по критерию числа точек поворота;
- независимости
уровней ряда остатков по d-критерию
(критические значения d1=1,10, d2=1,37) и
по первому коэффициенту автокорреляции при критическом значении r1=0,32;
- нормальности
распределения остаточной компоненты по R/S-критерию с
критическими значениями 3 и 4,21.
4) Отразить на графике фактические, расчетные и
прогнозные данные.
РЕШЕНИЕ:
Для
построения модели Хольта-Уинтерса проведем основные вычисления в таблице 1, а
вспомогательные вычисления в таблице 2.
Сначала
заполним вспомогательную таблицу.
В графу
Y(t) вспомогательной таблицы внесем первые 8 значений исходных данных
Во
вспомогательной таблице 2 для t и Y(t)
вычислим средние значения.
Проведем
вычисления t-tср, Y-Yср, (t-tср)*(Y(t)-Yср), (t-tср)2 и внесем в соответствующие графы таблицы 2
Затем,
для вычисленных значений сосчитаем их
суммы и перейдем к вычислениям в основной таблице 1.
Таблица 2 (вспомогательная)
|
|
t
|
Y(t)
|
Yr1(t)
|
t-tsr
|
Y-Ysr
|
(t-tsr)(Y(t)-Ysr)
|
(t-tsr)*(t-tsr)
|
|
1
|
33
|
38,4167
|
-3,5
|
-8,25
|
28,875
|
12,25
|
|
2
|
42
|
39,2262
|
-2,5
|
0,75
|
-1,875
|
6,25
|
|
3
|
50
|
40,0357
|
-1,5
|
8,75
|
-13,125
|
2,25
|
|
4
|
33
|
40,8452
|
-0,5
|
-8,25
|
4,125
|
0,25
|
|
5
|
36
|
41,6548
|
0,5
|
-5,25
|
-2,625
|
0,25
|
|
6
|
46
|
42,4643
|
1,5
|
4,75
|
7,125
|
2,25
|
|
7
|
56
|
43,2738
|
2,5
|
14,75
|
36,875
|
6,25
|
|
8
|
34
|
44,0833
|
3,5
|
-7,25
|
-25,375
|
12,25
|
|
СУММА
|
|
|
|
0
|
0
|
34
|
42
|
|
СР.ЗНАЧ
|
4,5
|
41,25
|
|
|
|
|
|
В столбец Y(t), строки 1-16
основной таблицы внесем исходные данные.
Значения а(0) и b(0) основной таблицы рассчитаем по формулам: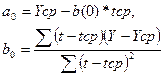 
.
Таблица 1(основная)
|
t
|
Y(t)
|
Yr(t)
|
a(t)
|
b(t)
|
F(t)
|
|
-3
|
|
|
|
|
0,8616
|
|
-2
|
|
|
|
|
1,0770
|
|
-1
|
|
|
|
|
1,2715
|
|
0
|
|
|
37,60714
|
0,8095
|
0,7896
|
|
1
|
33
|
33,1007
|
38,3816
|
0,7990
|
0,8605
|
|
2
|
42
|
42,1970
|
39,1257
|
0,7825
|
1,0749
|
|
3
|
50
|
50,7427
|
39,733
|
0,7300
|
1,2636
|
|
4
|
33
|
31,9494
|
40,8621
|
0,8497
|
0,8004
|
|
5
|
36
|
35,8939
|
41,7488
|
0,8608
|
0,8616
|
|
6
|
46
|
45,7999
|
42,6654
|
0,8776
|
1,0768
|
|
7
|
56
|
55,0224
|
43,7751
|
0,9472
|
1,2730
|
|
8
|
34
|
35,7955
|
44,0493
|
0,7453
|
0,7833
|
|
9
|
39
|
38,5945
|
44,9358
|
0,7876
|
0,8654
|
|
10
|
50
|
49,2369
|
45,936
|
0,8514
|
1,0838
|
|
11
|
59
|
59,5610
|
46,6552
|
0,8118
|
1,2680
|
|
12
|
37
|
37,1797
|
47,3981
|
0,7911
|
0,7817
|
|
13
|
44
|
41,7020
|
48,9859
|
1,0301
|
0,8851
|
|
14
|
54
|
54,2083
|
49,9583
|
1,0128
|
1,0821
|
|
15
|
65
|
64,6295
|
51,0588
|
1,0391
|
1,2710
|
|
16
|
40
|
40,7241
|
51,82
|
0,9557
|
0,7758
|
Во
вспомогательной таблице вычислим значения Yr1(t). Для этого воспользуемся
формулой Yr1(t) =a(0)+t*b(0)
Получаем
линейную модель Yr1(t) = 37,607 + 0,809t
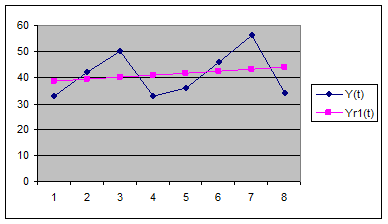
Для
визуальной проверки полученных значений построим графики Y(t), Yr1(t).
Получим:
Для исчисления F(-3) воспользуемся формулой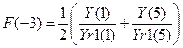 
,
F(-2), F(-1), F(0) рассчитаем
по аналогии.
В
основной таблице 1 a(t), b(t), F(t), и Yr(t) рассчитаем по соответствующим формулам:
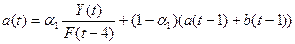
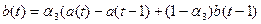
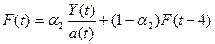
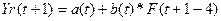
Мы
построили мультипликативную модель Хольта-Уинтерса.
Теперь
проверим нашу модель на точность, качество и адекватность. Для этого все
необходимые расчеты проведем в таблице 3.
Графы
Y(t) и Yr(t) заполним из
таблицы 1.
Таблица
3 (проверка точности и адекватности)
|
t
|
Y(t)
|
Yr(t)
|
E(t)
|
отн.
погр.
|
т.
Поворота
|
E(t)**2
|
(E(t)-E(t-1))**2
|
E(t)*E(t-1)
|
|
1
|
33
|
33,1007
|
-0,1007
|
0,30528
|
|
0,010
|
|
|
|
2
|
42
|
42,197
|
-0,197
|
0,46913
|
0
|
0,039
|
0,00927212
|
0,01985
|
|
3
|
50
|
50,7427
|
-0,7427
|
1,48547
|
1
|
0,552
|
0,29778761
|
0,14634
|
|
4
|
33
|
31,9494
|
1,05056
|
3,18353
|
1
|
1,104
|
3,21591667
|
-0,7803
|
|
5
|
36
|
35,8939
|
0,10606
|
0,2946
|
1
|
0,011
|
0,8920936
|
0,11142
|
|
6
|
46
|
45,7999
|
0,20009
|
0,43499
|
0
|
0,040
|
0,00884308
|
0,02122
|
|
7
|
56
|
55,0224
|
0,97759
|
1,7457
|
1
|
0,956
|
0,60450593
|
0,19561
|
|
8
|
34
|
35,7955
|
-1,7955
|
5,28086
|
1
|
3,224
|
7,69000448
|
-1,7553
|
|
9
|
39
|
38,5945
|
0,40548
|
1,0397
|
0
|
0,164
|
4,84428308
|
-0,728
|
|
10
|
50
|
49,2369
|
0,76308
|
1,52615
|
1
|
0,582
|
0,12787371
|
0,30941
|
|
11
|
59
|
59,561
|
-0,561
|
0,95086
|
1
|
0,315
|
1,75320329
|
-0,4281
|
|
12
|
37
|
37,1797
|
-0,1797
|
0,48573
|
0
|
0,032
|
0,14538275
|
0,10082
|
|
13
|
44
|
41,702
|
2,29805
|
5,22283
|
1
|
5,281
|
6,13932357
|
-0,413
|
|
14
|
54
|
54,2083
|
-0,2083
|
0,38581
|
1
|
0,043
|
6,28194789
|
-0,4788
|
|
15
|
65
|
64,6295
|
0,37047
|
0,56995
|
1
|
0,137
|
0,33501157
|
-0,0772
|
|
16
|
40
|
40,7241
|
-0,7241
|
1,81013
|
|
0,524
|
1,19796975
|
-0,2682
|
|
СУММ
|
|
|
|
|
10
|
13,01
|
33,5434191
|
-4,0242
|
|
СРЗНАЧ
|
|
|
|
1,57442
|
|
|
|
|
|
17
|
|
46,71088
|
|
|
|
|
|
|
|
18
|
|
58,14114
|
|
|
|
|
|
|
|
19
|
|
69,50804
|
|
|
|
|
|
|
|
20
|
|
43,16863
|
|
|
|
|
|
|
Рассчитаем
отклонения Е(t) = Y(t) - Yr(t) и квадрат отклонений E(t)2
Относительную погрешность рассчитаем как частное
абсолютных значений отклонений Е(t) и фактических значений Y(t) выраженное в процентах.
Таким образом, средняя относительная ошибка
аппроксимации это есть среднее арифметическое найденных относительных
погрешностей.
Относительная ошибка аппроксимации равна 1,57 %, она
не превышает 5 %, что позволяет сделать вывод о выполнении условия точности.
Проверим адекватность модели на основе исследования:
·
случайности
остаточной компоненты по критерию числа точек поворота
Для
этого, каждый уровень ряда Е(t) сравнивается
с двумя соседними. Если он больше (меньше) обоих соседних уровней, то точка
считается поворотной.
В
графе «Точки поворота» будем ставить 1, если точка поворотная и 0 в противном
случае.
Для
наглядности можно ряд Е(t) изобразить
графически, экстремумы графика будут соответствовать точкам поворота:
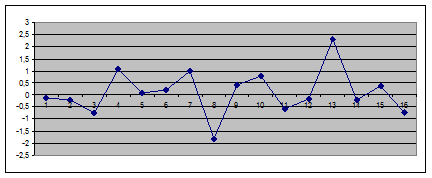
Вычисляем
число точек поворота (в нашем примере их 10) и сравниваем с пороговым значением
q.
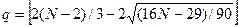= 6
Так
как p > q, то условие
случайности уровней выполнено.
·
независимости
уровней ряда остатков
- по d-критерию
Вычислим величину d-критерия по формуле: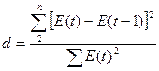 
Так
как все необходимы значения мы вычислили в таблице 3, то подставив их в
формулу, получим, что d-критерий равен
2,57. Так как он больше двух, то имеет место отрицательная автокорреляция и
следует уточнить значение d, вычитая его
из 4. Получим d' = 1,423.
Так
как расчетное значение больше 1-ой границы критического интервала и больше 2, проверим
независимость по первому коэффициенту автокорреляции.
- по первому коэффициенту автокорреляции
Вычислим величину r1 по формуле: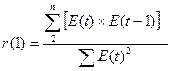 
= - 0,257
Так
как Ιr1Ι = 0,257 и он меньше критического уровня r1 = 0,32, теперь можно сделать вывод, что уровни ряда
остатков независимы.
·
нормальности
распределения остаточной компоненты
Вычислим величину RS-критерия 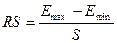по формуле: 
, где S –
среднеквадратическое отклонение, рассчитываемое по формуле: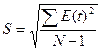 
=0,931
Тогда
расчетный RS = 4,395.
Табличное
значение границ для RS-критерия для N=16 и 5%-ого уровня значимости есть интервал от 3,00
до 4,21
Наше
расчетное значение не входит в этот интервал, значит, уровни ряда остатков не подчиняются
нормальному распределению.
Для
вычисления прогнозных значений Yr(t), t=17 рассчитаем по формуле:
Yr(17)=(a(16)+(t-16)*b(16))*F(t-4) = 46,71
Yr(18,19,20) рассчитаем аналогично. (см.
таблица 3)
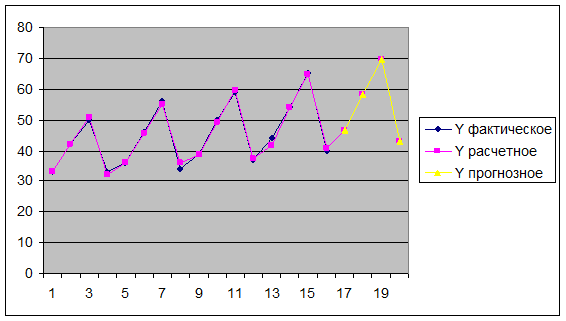
Отразим
на графике фактические, расчетные и прогнозные значения:
ЗАДАЧА 2
Даны цены (максимальная, минимальная, закрытия) за 10
дней. Интервал сглаживания принять равным пяти дням. Рассчитать:
- экспоненциальную скользящую среднюю,
- момент,
- скорость изменения цен,
- индекс относительной силы
- %R, %K, %D.
Расчеты проводить для всех дней, для
которых эти расчеты можно выполнить на основании имеющихся данных.
РЕШЕНИЕ:
Сформируем таблицу исходных
данных:
|
Дни
|
Цены
|
|
Макс.
|
Мин.
|
Закр.
|
|
1
|
744
|
705
|
709
|
|
2
|
743
|
675
|
738
|
|
3
|
750
|
700
|
735
|
|
4
|
759
|
707
|
751
|
|
5
|
770
|
740
|
755
|
|
6
|
776
|
661
|
765
|
|
7
|
756
|
715
|
720
|
|
8
|
745
|
685
|
739
|
|
9
|
758
|
725
|
740
|
|
10
|
730
|
673
|
678
|
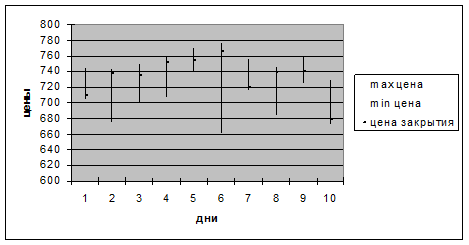
С
помощью Мастера Диаграмм построим биржевую диаграмму для набора из трех
значений ( максимальной цены, минимальной цены и цены закрытия)
СКОЛЬЗЯЩИЕ
СРЕДНИЕ:
Затем
рассчитаем экспоненциальную скользящую среднюю ЕМА по формуле: EMAi=k*Ci+(1-k)*EMAi-1. при i=6,…,10, n=5, k=2/(n+1)=1/3
Значение
EMA5
принимается равным средней цене закрытия за 1-5 дни.
Результаты
вычислений занесем в таблицу:
|
Дни
|
Макс.
|
Мин.
|
Закр.
|
ЕМА
|
|
1
|
744
|
705
|
709
|
|
|
2
|
743
|
675
|
738
|
|
|
3
|
750
|
700
|
735
|
|
|
4
|
759
|
707
|
751
|
|
|
5
|
770
|
740
|
755
|
737,60
|
|
6
|
776
|
661
|
765
|
746,73
|
|
7
|
756
|
715
|
720
|
737,82
|
|
8
|
745
|
685
|
739
|
738,21
|
|
9
|
758
|
725
|
740
|
738,81
|
|
10
|
730
|
673
|
678
|
718,54
|
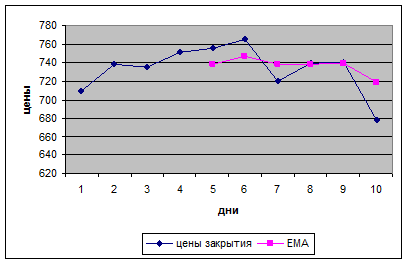
Построим
графики цены закрытия и экспоненциальной средней (в одной системе координат).
ОСЦИЛЛЯТОРЫ:
Для
вычисления осцилляторов сформируем таблицу и проведем необходимые вычисления по
формулам: MOMi=Ci – Ci-5,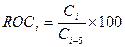 
(i=6,7,8,9,10),
Понижение и Повышение (i=2,3,…,10)
Вычислим
при i=6,…,10 AU и AD, где:
AUi - суммы повышений за предшествующие 5 дней, ADi - суммы понижений за предшествующие 5 дней,), RSIi=100-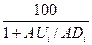
.
|
Дни
|
MOM
|
ROC
|
Пониж
|
Повыш.
|
AU
|
AD
|
RSI
|
|
1
|
|
|
|
|
|
|
|
|
2
|
|
|
|
29
|
|
|
|
|
3
|
|
|
3
|
|
|
|
|
|
4
|
|
|
|
16
|
|
|
|
|
5
|
|
|
|
4
|
49
|
3
|
94
|
|
6
|
56
|
108
|
|
10
|
30
|
3
|
91
|
|
7
|
-18
|
98
|
45
|
|
30
|
45
|
40
|
|
8
|
4
|
101
|
|
19
|
33
|
45
|
42
|
|
9
|
-11
|
99
|
|
1
|
30
|
45
|
40
|
|
10
|
-77
|
90
|
62
|
|
20
|
107
|
16
|
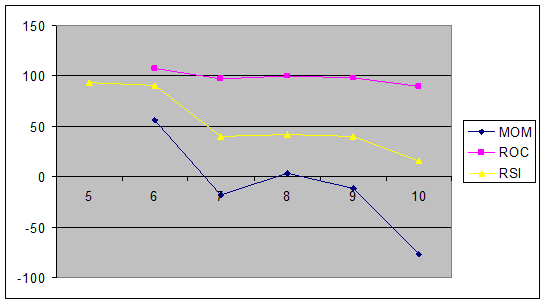
Построим графики МОМ, ROC, RSI
СТОХАСТИЧЕСКИЕ
ЛИНИИ:
Для
вычисления стохастических линий сформируем таблицу и произведем необходимые
вычисления :
Н5
– Максимальная цена за 5 дней
L5 – Минимальная цена за 5 дней
%K=100(Ct - L5)/ (H5 - L5),
%R=100(H5 - Ct)/ (H5 - L5) или100-%K
(вычисления
проводятся при i=5,6,…,10),
%D (вычисления проводятся
при i=7,8,9,10) равен отношению сумм
цена закрытия – минимальная цена и максимальная - минимальная цена за
три предшествующих дня.
|
Дни
|
цена закрытия
|
Макс.
|
Мин.
|
%K
|
%R
|
%D
|
|
1
|
709
|
744
|
705
|
|
|
-
|
|
2
|
738
|
743
|
675
|
|
|
-
|
|
3
|
735
|
750
|
700
|
|
|
|
|
4
|
751
|
759
|
707
|
|
|
|
|
5
|
755
|
770
|
740
|
84,21
|
15,7895
|
|
|
6
|
765
|
776
|
661
|
89,11
|
9,57
|
|
|
7
|
720
|
756
|
715
|
51,30
|
48,70
|
39,07
|
|
8
|
739
|
745
|
685
|
67,83
|
32,17
|
31,47
|
|
9
|
740
|
758
|
725
|
68,70
|
31,30
|
23,90
|
|
10
|
678
|
730
|
673
|
14,78
|
85,22
|
6,89
|
ЗАДАЧА 3
Выполнить
различные коммерческие расчеты, используя данные приведенные в таблице.
|
Сумма
|
Дата
превоначальная
|
Дата
конечная
|
Время в
днях
|
Время в
годах
|
Ставка
|
Число
начислений
|
|
S
|
Tн
|
Tк
|
Tдн
|
Tлет
|
i
|
m
|
|
2000 000
|
16.01.02
|
14.03.02
|
180
|
4
|
25
|
2
|
РЕШЕНИЕ:
3.1. Банк выдал ссуду, размером S
руб. Дата выдачи ссуды - Тн, возврата - Тк.
День выдачи и день возврата считать за 1 день. Проценты
рассчитываются по простой процентной
ставке i % годовых. Найти:
1. точные проценты с точным числом дней ссуды;
2. обыкновенные проценты с точным числом дней ссуды;
3. обыкновенные проценты с приближенным числом дней
ссуды.
Формула
расчета процентов по простой процентной ставки S = p(1 + ni), где S – сумма к получению, p – вложенная
сумма, i –
процентная ставка, n – срок
вклада в годах.
Таким
образом:
1) S = 2000 000*( 1 + 0,25*57/365)
= 2078082,19 руб.
Следовательно проценты будут равны 2078082,19 – 2000 000= 78082,19 руб.
2) S = 2000 000*( 1 + 0,25*57/360)
= 2079166,67 руб.
Следовательно проценты будут равны 2079166,67 – 2000 000= 79166,
67 руб.
3) S = 2000000*( 1 + 0,25*59/360)
= 2081944,44 руб.
Следовательно проценты будут равны 2081944,44 – 2000000=
81944,44 руб.
3.2. Через Тдн дней после подписания договора должник уплатит S руб. Кредит
выдан под i% годовых (проценты обыкновенные). Какова первоначальная сумма и
дисконт?
Первоначальную
сумму р можно найти из формулы простых процентов:
,
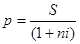
где n -
срок вклада в годах
Таким
образом р = 2000 000/ ( 1 + 180/360
*0,25) = 1777777,78 руб.
Сумма
дисконта считается как разница между уплаченной в конце и в начале суммой:
D
= S – P
D
= 2000000– 1777777,78 = 222222,22 руб
3.3 Через Тдн дней предприятие должно получить по векселю
S руб. Банк приобрел этот вексель с дисконтом. Банк учел вексель по учетной
ставке i% годовых (год равен 360 дням).
Определить полученную предприятием сумму и дисконт.
Находим
сумму дисконта D = Sni, где n - срок вклада
в годах, который можно найти как:
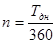
D
= 2000 000* 180/360 * 0,25 = 250 000 руб.
Таким образом, полученная предприятием сумма по
векселю составит :
Р
= S – D = 2000 000 – 250 000 =
1750 000 руб.
3.4. В кредитном договоре на сумму S руб. и сроком на Тлет лет,
зафиксирована ставка сложных процентов, равная i% годовых. Определить
наращенную сумму.
Формула
расчета по сложной процентной ставке S = p(1 + i)n,
где S – сумма к
получению, p – вложенная
сумма, i –
процентная ставка, n – срок
вклада в годах.
Таким
образом, сумма к получению составит:
S = 2000 000 * (1 + 0,25)4 = 4882812,5
руб
Сумма
процентов по вкладу составит 4882812,5 – 2000 000 = 2882812,5 руб.
3.5. Ссуда, размером S
руб. предоставлена на Тлет. Проценты сложные, ставка - i% годовых.
Проценты начисляются m раз в году. Вычислить
наращенную сумму.
Воспользуемся
формулой для исчисления номинальной процентной ставки:
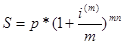
где S – сумма к
получению, p – вложенная
сумма, i(m) –
процентная ставка выплачиваемая m раз в год, n – срок вклада в годах.
Таким
образом, сумма к получению составит:
S = 2000 000 (1 +
0,25/2)2*4 = 5131569,03 руб.
Сумма
процентов по вкладу составит 5131569,03 - 2000 000 = 3131569,03руб.
3.6. Вычислить эффективную ставку процента, если банк начисляет проценты m
раз в году, исходя из номинальной ставки i% годовых.
Для
вычисления воспользуемся формулой:
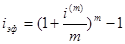
Таким
образом, эффективная процентная ставка составит ( 1 + 0,25/2)2 – 1 = 0,2656 или
26,56 %
3.7. Определить, какой должна быть номинальная ставка при начислении
процентов m раз в году, чтобы обеспечить
эффективную ставку i% годовых.
Преобразуем
формулу для исчисления эффективной ставки и получим:
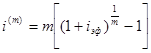
Таким образом, номинальная ставка
будет равна 2[(1+0,25)0,5 – 1] = 0,2361 или 23,61 %
3.8. Через Тлет„ предприятию будет выплачена сумма S руб. Определить ее
современную стоимость при условии, что применяется сложная процентная ставка i%
годовых.
Воспользуемся формулой
S = p(1 + i)n для расчета по сложной процентной ставке,
и преобразовав её получим формулу:
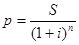
Таким
образом, современная стоимость вклада будет равна:
р
= 2000 000/ (1 + 0,25)4 = 819200 руб.
3.9. Через Тлет по векселю должна быть выплачена сумма S руб. Банк учел
вексель по сложной учетной ставке i% годовых. Определить дисконт.
Воспользуемся
формулами: P = S(1 – d)n и D = S – P, где S – сумма к получению, p – вложенная
сумма, d –
процентная ставка
Получим:
Первоначальная
сумма составит 2000 000( 1- 0,25)4 = 632812,5 руб.
Дисконт
равен 2000 000 – 632812,5 = 1367187,5 руб.
3.10. В течение Тлет лет на расчетный счет в конце каждого года поступает по
S руб., на которые m раз в году начисляются проценты по
сложной годовой ставке i %. Определить сумму на расчетном счете к концу
указанного срока.
Имеем
поток платежей постнумерандо, где R = 2000 000 руб.
Конечная
сумма определяется по формуле: S = RsnΙiэф, где snΙiэф = ((1 + iэф)n-1) / iэф
Эффективную
процентную ставку возьмём из задачи 3.6. Она равна 26,56 %
Таким
образом, получим:
S = 2000 000 * ((1+ 0,2656)4-1)/ 0,2656 = руб.