МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО
ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ
ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА ЭКОНОМИКО-МАТЕМАТИЧЕСКИХ МЕТОДОВ И МОДЕЛЕЙ
КОНТРОЛЬНАЯ РАБОТА
по дисциплине
финансовая математика
Вариант
№ 6
Задание 1.
Приведены поквартальные данные о кредитах от
коммерческого банка на жилищное строительство (в условных единицах) за 4 года
(всего 16 кварталов).
Таблица 1
|
Квартал
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
|
Кредит от коммерческого банка на жилищное строительство
|
36
|
46
|
55
|
35
|
39
|
50
|
61
|
37
|
42
|
54
|
64
|
40
|
47
|
58
|
70
|
43
|
Требуется:
1. Построить адаптивную мультипликативную модель Хольта-Уинтерса
с учетом сезонного фактора, приняв параметры сглаживания α1=0,3;α2=0,6;
α3=0,3.
2. Оценить точность построенной модели с использованием
средней относительной ошибки аппроксимации.
3. Оценить адекватность построенной модели на основе
исследования:
· случайности остаточной компоненты по критерию пиков;
· независимости
уровней ряда остатков по d-критерию
(критические значения d1=1,10 и d2=1,37) и по первому коэффициенту автокорреляции при
критическом значении r1=0,32;
· нормальности распределения остаточной компоненты по R/S-критерию с
критическими значениями от 3 до 4,21.
4. Построить точечный прогноз на 4 шага вперед, т.е. на 1
год.
5. Отразить на графике фактические, расчетные и
прогнозные данные.
Решение:
1
Мультипликативная
модель Хольта-Уинтерса с линейным ростом имеет следующий вид:
где k -
период упреждения;
Yp(t) - расчетное значение экономического показателя для
t-го периода;
a(t), B(t),
F(t) - коэффициенты модели; они
адаптируются, уточняются по мере перехода от членов ряда с номером t-1 к t;
F(t+k-L) - значение коэффициента сезонности того периода, для которого
рассчитывается экономический показатель;
L - период сезонности (для квартальных данных L=4).
Коэффициенты
модели a(t), b(t) и F(t) рассчитываются по формулам:
|
a(t)=α1*Y(t)/F(t-L)+(1-α1)*[a(t 1)+b(t-1)];
|
|
b(t)=α3*[a(t)-a(t-1)]+(1-α3)*b(t-1);
|
|
F(t)=α2*Y(t)/a(t)+(1-α2)*F(t-L).
|
|
Для расчета a(1) и b(1) необходимо оценить значения этих коэффициентов для
предыдущего период времени (т.е. для t=1-1=0).
Значения a(0) и b(0) имеют смысл этих же коэффициентов для четвертого
квартала года, предшествующего коэффициентов для четвертого квартала года,
предшествующего первому году, для которого имеются данные (таб. 1).
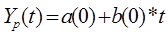 Для оценки начальных значений a(0) и b(0) применим
линейную модель к первым 8 значениям Y(t) из
таблицы. Линейная модель имеет вид:
Для оценки начальных значений a(0) и b(0) применим
линейную модель к первым 8 значениям Y(t) из
таблицы. Линейная модель имеет вид:
Таблица 2
Промежуточные расчеты
для вычисления коэффициентов
|
|
t
|
Y(t)
|
Y(t)-Yср
|
t-tср
|
(t-tср)2
|
(Y(t)-Yср)*(t-tср)
|
Yp(t)
|
|
|
1
|
36
|
-8,9
|
-3,5
|
12,3
|
31,1
|
51,4
|
|
|
2
|
46
|
1,1
|
-2,5
|
6,3
|
-2,8
|
46,4
|
|
|
3
|
55
|
10,1
|
-1,5
|
2,3
|
-15,2
|
43,0
|
|
|
4
|
35
|
-9,9
|
-0,5
|
0,3
|
4,9
|
41,3
|
|
|
5
|
39
|
-5,9
|
0,5
|
0,3
|
-2,9
|
41,3
|
|
|
6
|
50
|
5,1
|
1,5
|
2,3
|
7,7
|
43,0
|
|
|
7
|
61
|
16,1
|
2,5
|
6,3
|
40,3
|
46,4
|
|
|
8
|
37
|
-7,9
|
3,5
|
12,3
|
-27,6
|
51,4
|
|
сумму
|
|
359
|
|
|
42
|
35,5
|
364,07
|
|
среднее
|
4,5
|
44,875
|
|
|
5,25
|
|
|
Метод наименьших квадратов дает возможность определить
коэффициенты линейного уравнения a(0)
и b(0) по следующим формулам:
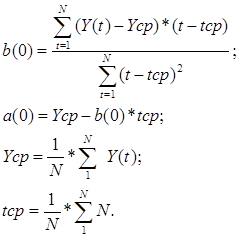
Применяя линейную модель к первым 8 значениям ряда из
таблицы 1 (т.е. к данным за первые 2 года), находим значения a(0), b(0).
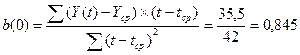
a(0) = Yср – b(0)*tср = 44,9 - 0,845*4,5=41,07.
Тогда линейное уравнение будет иметь вид: Yp(t)=41,07+0,845*t
Из этого уравнения находим расчетные значения Yp(t) и сопоставляем их с фактическими
значениями.
(таб. 3).
Таблица
3
Сопоставление фактических данных Y(t) и рассчитанных по линейной модели значений Yp(t)
|
t
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
Y(t)
|
36
|
46
|
55
|
35
|
39
|
50
|
61
|
37
|
|
Yp(t)
|
41,92
|
42,76
|
43,61
|
44,45
|
45,30
|
46,14
|
46,99
|
47,83
|
Такое сопоставление позволяет оценить приближенные
значения коэффициентов сезонности I-IV кварталов F(-3), F(-2), F(-1) и F(0) для года, предшествующего первому году,
по которому имеются данные в таблице 1. Эти значения необходимы для расчета
коэффициентов сезонности первого года F(1),
F(2), F(3), F(4) и других параметров модели Хольта-Уинтерса. Коэффициент сезонности есть отношение
фактического значения экономического показателя к значению, рассчитанному по
линейной модели. Поэтому в качестве оценки коэффициента сезонности I квартала F(-3) может служить отношение
фактических и расчетных значений Y(t)
I квартала первого года, равное Y(1)/Yp(1),
и такое же отношение для I квартала второго года (т.е. за V квартал t=5) Y(5)/Yp(5). Для окончательной, более
точной, оценки этого коэффициента сезонности можно использовать среднее
арифметическое значение этих двух величин. F(-3)=[Y(1)/Yp(1)+Y(5)/Yp(5)]/2= 0,8599,
Аналогично находим оценки коэффициента сезонности для
II, III и IV кварталов:
F(-2)=[Y(2)/Yp(2)+Y(6)/Yp(6)]/2=1,0797;
F(-1)=[Y(3)/Yp(3)+Y(7)/Yp(7)]/2=1,2797$
F(0)=[Y(4)/Yp(4)+Y(8)/Yp(8)]/2=0,7804;
Оценив значения a(0), b(0), а также
F(-3), F(-2), F(-1), F(0), можно перейти к построению адаптивной
мультипликативной модели Хольта-Уинтерса с помощью формул.
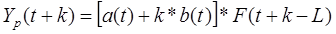 Рассчитаем значения Yp(t), a(t), b(t) и F(t) для t=1.
Рассчитаем значения Yp(t), a(t), b(t) и F(t) для t=1.
Полагая что t=0, k=1, находим Yp(1):
Yp(0+1)=Yp(1)=[a(0)+1*b(0)]*F(0+1-4)=[a(0)+1*b(0)]*F(-3)=36,04
Из уравнений, полагая, что t=1, находим:
a(1)=α1*Y(1)/F(-3)+(1-α1)*[a(0)+b(0)]=41,90
b(1)=α3*[a(1)-a(0)]+(1-α3)*b(0)= 0,84
F(1)=α2*Y(1)/a(1)+(1-α2)*F(-3)=0,8595;
Аналогично рассчитаем значения Yp(T), a(t). B(t) и F(t) для t=2
Yp(2)=[a(1)+1*b(1)]*F(-2)=46,15
a(2)=α1*Y(2)/F(-2)+(1-α1)*[a(1)+b(1)]=42,70
b(2)=α3*[a(2)-a(1)]+(1-α3)*b(1)=0,83
F(2)=α2*Y(2)/a(2)+(1-α2)*F(-2)=1,0782;
для t=3:
Yp(3)=[a(2)+1*b(2)]*F(-1)=55,71
a(3)=α1*Y(3)/F(-1)+(1-α1)*[a(2)+b(2)]=43,36
b(3)=α3*[a(3)-a(2)]+(1-α3)*b(2)=0,78
F(3)=α2*Y(3)/a(3)+(1-α2)*F(-1)=1,2729;
для t=4:
Yp(4)=[a(3)+1*b(3)]*F(0)=35,27
a(4)=α1*Y(4)/F(0)+(1-α1)*[a(3)+b(3)]=44,35
b(4)=α3*[a(4)-a(3)]+(1-α3)*b(3)=0,84
F(4)=α2*Y(4)/a(4)+(1-α2)*F(0)=0,7856
для t=5:
Yp(5)=[a(4)+1*b(4)]*F(1)=38.84
a(5)=α1*Y(5)/F(1)+(1-α1)*[a(4)+b(4)]=45,25
b(5)=α3*[a(5)-a(4)]+(1-α3)*b(4)=0,86
F(5)=α2*Y(5)/a(5)+(1-α2)*F(1)=0,8609;
Продолжая аналогично для t=6,7,8,…16, строится
модель Хольта-Уинтерса. При
использовании MS Office Excel составим следующую таблицу с
введением соответствующих формул в нужные ячейки, что облегчит процесс
вычисления (таб. 4).
Таблица 4
|
t
|
Y(t)
|
a(t)
|
b(t)
|
F(t)
|
Yp(t)
|
Абсолютная погрешность Е(t)
|
Относительная погрешность в %
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
|
-3
|
|
|
|
0,8599
|
|
|
|
|
|
-2
|
|
|
|
1,0797
|
|
|
|
|
|
-1
|
|
|
|
1,2797
|
|
|
|
|
|
0
|
|
|
|
0,7804
|
|
|
|
|
|
1
|
36
|
41,90
|
0,84
|
0,8595
|
36,04
|
-0,0445
|
-0,001237
|
|
|
2
|
46
|
42,70
|
0,83
|
1,0782
|
46,15
|
-0,1464
|
-0,003183
|
|
|
3
|
55
|
43,36
|
0,78
|
1,2729
|
55,71
|
-0,7059
|
-0,012835
|
|
|
4
|
35
|
44,35
|
0,84
|
0,7856
|
35,27
|
-0,2726
|
-0,007790
|
|
|
5
|
39
|
45,25
|
0,86
|
0,8609
|
38,84
|
0,1558
|
0,003995
|
|
|
6
|
50
|
46,19
|
0,88
|
1,0808
|
49,72
|
0,2848
|
0,005697
|
|
|
7
|
61
|
47,33
|
0,96
|
1,2825
|
59,92
|
1,0848
|
0,017783
|
|
|
8
|
37
|
47,93
|
0,85
|
0,7775
|
37,93
|
-0,9344
|
-0,025254
|
|
|
9
|
42
|
48,78
|
0,85
|
0,8610
|
41,99
|
0,0052
|
0,000123
|
|
|
10
|
54
|
49,73
|
0,88
|
1,0838
|
53,64
|
0,3554
|
0,006582
|
|
|
11
|
64
|
50,40
|
0,82
|
1,2749
|
64,91
|
-0,9141
|
-0,014282
|
|
|
12
|
40
|
51,29
|
0,84
|
0,7789
|
39,82
|
0,1801
|
0,004502
|
|
|
13
|
47
|
52,87
|
1,06
|
0,8778
|
44,88
|
2,1214
|
0,045137
|
|
|
14
|
58
|
53,80
|
1,02
|
1,0803
|
58,45
|
-0,4457
|
-0,007685
|
|
|
15
|
70
|
54,85
|
1,03
|
1,2757
|
69,90
|
0,1018
|
0,001454
|
|
|
16
|
43
|
55,68
|
0,97
|
0,7750
|
43,53
|
-0,5271
|
-0,012258
|
|
|
Итого:
|
779
|
|
|
|
|
0,30
|
8,00
|
|
2
Проверка точности
модели
Условие точности выполняется, если относительная
погрешность в среднем не превышает 5%. Суммарное значение относительных
погрешностей составляет 8,00, что дает среднюю величину 8,00/16=0,5%. -0,5<5%
Следовательно,
условие точности выполнено.
3
Проверка условия
адекватности.
Проверка
случайности уровней. Проверку
случайности уровней остаточной компоненты проводим на основе критерия
поворотных точек (табл.5).
Таблица 5
Промежуточные расчеты для оценки
адекватности модели
|
t
|
E(t)
|
Точки поворота
|
E(t)2
|
[E(t)-E(t-1)]2
|
E(t)*E(t-1)
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
-0,045
|
-
|
0,002
|
-
|
-
|
|
2
|
-0,146
|
1
|
0,021
|
0,010
|
0,007
|
|
3
|
-0,706
|
0
|
0,498
|
0,313
|
0,103
|
|
4
|
-0,273
|
0
|
0,074
|
0,188
|
0,192
|
|
5
|
0,156
|
0
|
0,024
|
0,184
|
-0,042
|
|
6
|
0,285
|
0
|
0,081
|
0,017
|
0,044
|
|
7
|
1,085
|
1
|
1,177
|
0,640
|
0,309
|
|
8
|
-0,934
|
1
|
0,873
|
4,077
|
-1,014
|
|
9
|
0,005
|
0
|
0,000
|
0,883
|
-0,005
|
|
10
|
0,355
|
1
|
0,126
|
0,123
|
0,002
|
|
11
|
-0,914
|
1
|
0,835
|
1,612
|
-0,325
|
|
12
|
0,180
|
0
|
0,032
|
1,197
|
-0,165
|
|
13
|
2,121
|
1
|
4,500
|
3,769
|
0,382
|
|
14
|
-0,446
|
1
|
0,199
|
6,590
|
-0,946
|
|
15
|
0,102
|
1
|
0,010
|
0,300
|
-0,045
|
|
16
|
-0,527
|
-
|
0,278
|
0,396
|
-0,054
|
|
Сумма
|
2,298
|
8
|
12,733
|
25,297
|
-1,555
|
Общее число поворотных точек в нашем примере равно p=8
Рассчитаем значение q:
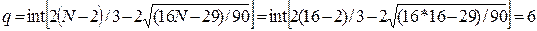
Если количество поворотных точек p
больше q, то условие случайности уровней выполнено. В нашем
случае p=8, q=6, значит условие случайности уровней ряда выполнено.
Проверка
независимости уровней ряда остатков.
а) по d-критерию Дарбина-Уотсона
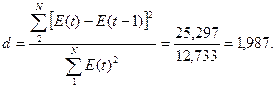
В нашем случае d2<d<2, 1,37<1,987<2.
Уровни ряда остатков являются независимыми.
б) по первому коэффициенту автокорреляции
Если модуль рассчитанного значения первого
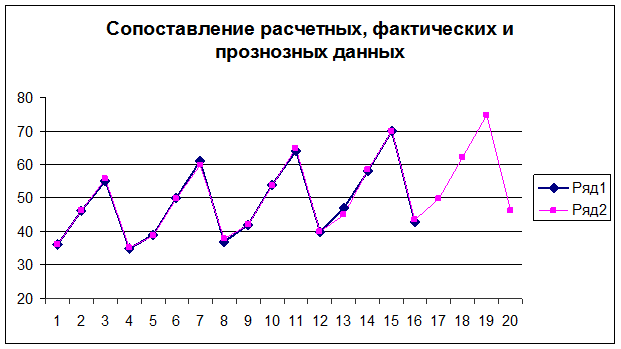
коэффициента автокорреляции меньше критического значения r(1)<r
табл., то уровни ряда остатков независимы. В нашей задаче |r(1)|=0,122<rтаб=0,32
– условие независимости выполняется.
Проверка
соответствия ряда остатков нормальному распределению определяем по RS –критерию. Рассчитаем значение RS:
RS=(Emax
– Emin)/S,
где Emax -
максимальное значение уровней ряда остатков E(t),
Emin - минимальное значение уровней ряда остатков E(t),
S - среднее квадратическое отклонение;
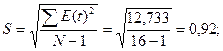
Emax=2,121
Emin=-0,934
RS= (2,121-(-0,934))/0,92=3,41
Полученное значение попадает в заданный интервал,
уровни ряда остатков подчиняются нормальному распределению остаточной
компоненты по R/S-критерию с критическими значениями от 3 до 4,21.
4
Построение
точечного прогноза
Составим прогноз на 4 квартала вперед (т.е. на 1 год,
с t=17 по t=20).
Максимальное значение t, для которого могут быть рассчитаны коэффициенты a(t), b(t) определяется количеством
исходных данных и равно 16.
Рассчитав значения a(16),
b(16) можно определить прогнозные значения экономического показателя Yp(t).
Для t=17 имеем:
Yp(17)=Yp(16+1)=[a(16)+1*b(16)]*F(16+1-4)=49,7
Yp(18)=Yp(16+2)=[a(16)+2*b(16)]*F(16+2-4)=62,2
Yp(19)=Yp(16+3)=[a(16)+3*b(16)]*F(16+3-4)=74,7
Yp(20)=Yp(16+4)=[a(16)+4*b(16)]*F(16+4-4)= 46,2
Рис. 1
Задание № 2.
Даны цены (открытия, максимальная,
минимальная и закрытия) за 10 дней. Интервал сглаживания принять равным пяти
дням. Рассчитать:
- экспоненциальную скользящую среднюю;
- момент;
- скорость изменения цен;
- индекс относительной силы;
- %R, %K, %D.
Расчеты проводить для всех дней, для
которых эти расчеты можно выполнить на основании имеющихся данных (таб. 6).
Таблица 6
|
Дни
|
Цены
|
|
макс.
|
мин.
|
закр.
|
|
1
|
600
|
550
|
555
|
|
2
|
560
|
530
|
530
|
|
3
|
536
|
501
|
524
|
|
4
|
545
|
521
|
539
|
|
5
|
583
|
540
|
569
|
|
6
|
587
|
562
|
581
|
|
7
|
582
|
561
|
562
|
|
8
|
573
|
556
|
573
|
|
9
|
610
|
579
|
592
|
|
10
|
645
|
585
|
645
|
Решение:
1.
Экспоненциальная
скользящая средняя.
EMAt= Ct*k+EMAt-1*(1-k),
где k=2/(n+1)
Ct – цена закрытия t-го дня
Таблица 7
Расчет 10-дневной ЕМА и ее сравнение с МА
|
Дни
|
Цены
|
МАt
|
EMAt
|
(графа4-графа5)
(Ct- МАt)
|
(графа4-графа6)
(Ct- ЕМАt)
|
|
макс. цена
Ht
|
мин. цена
Lt
|
цена закрытия
Ct
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
1
|
600
|
550
|
555
|
|
|
|
|
|
2
|
560
|
530
|
530
|
|
|
|
|
|
3
|
536
|
501
|
524
|
|
|
|
|
|
4
|
545
|
521
|
539
|
|
|
|
|
|
5
|
583
|
540
|
569
|
543,4
|
543,4
|
25,6
|
25,6
|
|
6
|
587
|
562
|
581
|
548,6
|
555,9
|
32,4
|
25,1
|
|
7
|
582
|
561
|
562
|
555
|
558,0
|
7
|
4,0
|
|
8
|
573
|
556
|
573
|
564,8
|
563,0
|
8,2
|
10,0
|
|
9
|
610
|
579
|
592
|
575,4
|
572,6
|
16,6
|
19,4
|
|
10
|
645
|
585
|
645
|
590,6
|
596,8
|
54,4
|
48,2
|
2.
Момент
MOMt=Ct – Ct-n
Положительные значения МОМ свидетельствуют об
относительном росте цен, отрицательные – о снижении
3.
Скорость
изменения цен
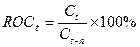
ROC
является отражением скорости изменения
цены, а также указывает направление этого изменения.
4.
Индекс
относительной силы
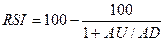 ,
,
где AU – сумма приростов конечных цен за n последних дней;
AD – сумма
убыли конечных цен за n последних
дней.
Таблица 8
Расчет МОМ, ROC и RSI
|
Дни
|
Цена закрытия
Ct
|
МОМ
|
ROC
|
повышение цены
|
понижение цены
|
Сумма повышения
AU
|
Сумма понижения
AD
|
RSI
|
|
1
|
555
|
|
|
|
|
|
|
|
|
2
|
530
|
|
|
|
25
|
|
|
|
|
3
|
524
|
|
|
|
6
|
|
|
|
|
4
|
539
|
|
|
15
|
|
|
|
|
|
5
|
569
|
14
|
102,5
|
30
|
|
|
|
|
|
6
|
581
|
51
|
109,6
|
12
|
|
57
|
31
|
64,8
|
|
7
|
562
|
38
|
107,3
|
|
19
|
57
|
25
|
69,5
|
|
8
|
573
|
34
|
106,3
|
11
|
|
68
|
19
|
78,2
|
|
9
|
592
|
23
|
104,0
|
19
|
|
72
|
19
|
79,1
|
|
10
|
645
|
64
|
111,0
|
53
|
|
95
|
19
|
83,3
|
5.
Стохастические
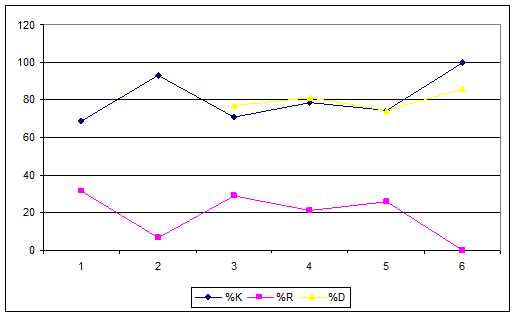
линии (таб. 9).
%Kt=100*(Ct – L5)/(H5
– L5);
%Rt=100*(H5 – Ct)/(H5
– L5);
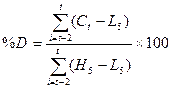 ;
;
где Ct – цена закрытия текущего дня.
L5 и H5 – минимальная и максимальная цены за 5 предшествующих
дней, включая текущий.
Таблица 9
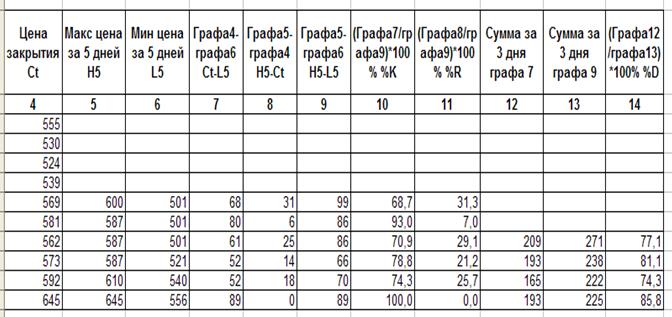
Рис. 2
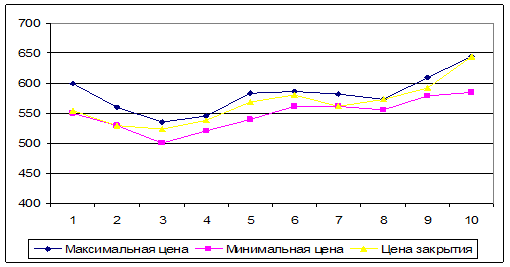
Рис. 3
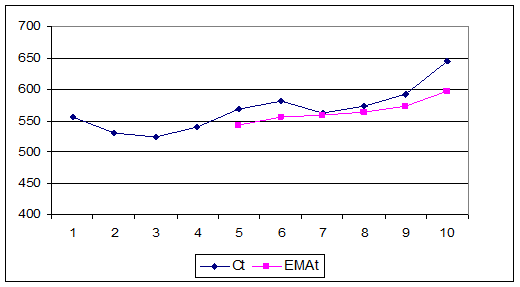
Рис. 4
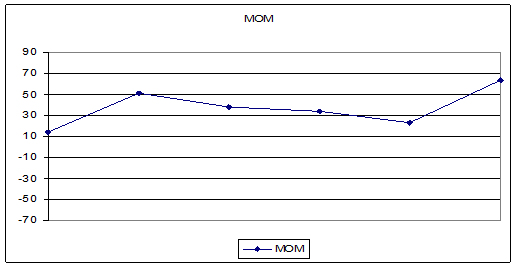
Рис. 5
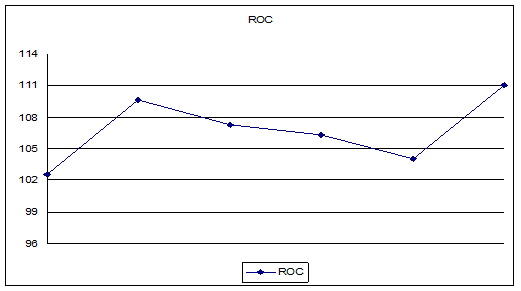
Рис. 6
 Задание №3
Задание №3
Выполнить различные коммерческие расчеты, используя
данные, приведенные в таблице 10. В условии задачи значения параметров
приведены в виде переменных. По именам переменных из таблицы необходимо выбрать
соответствующие численные значения параметров и выполнить расчеты.
Таблица 10
|
сумма
|
Дата начальная
|
Дата конечная
|
Время в днях
|
Время в годах
|
ставка
|
Число начислений
|
|
S
|
Тн
|
Тк
|
Тдн
|
Тлет
|
i
|
m
|
|
3 000 000
|
14.01.02
|
18.03.02
|
90
|
5
|
35
|
4
|
1.
Банк выдал ссуду,
размером 3 000 000 руб. Дата выдачи ссуды 14.01.02, возврата – 18.03.02. День
выдачи и день возврата считать за 1 день. Проценты рассчитываются по простой
процентной ставке 35 % годовых. Найти:
· точные проценты с точным числом дней ссуды;
· обыкновенные проценты с точным числом дней ссуды;
· обыкновенные проценты с приближенным числом дней
ссуды.
Решение:
I = S·n·i
где n = t/K
·
t=17+28+17+1=63
К
= 365; t = 63; I = 3 000 000 · 63 / 365 ·
0,35
= 181 232,88 руб.;
·
К = 360; t = 53; I = 3 000 000
· 63 / 360 · 0,35 = 183 750 руб.;
·
t = 16 + 30 + 18 = 64
К
= 360; t = 64; I = 3 000 000
· 64 / 360 · 0,35 = 186 666,67 руб.
2
Через 90 дней после подписания договора должник
уплатит 3 000 000 руб. Кредит выдан под 35% годовых (проценты
обыкновенные). Какова первоначальная сумма и дисконт?
Решение:
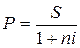 - первоначальная сумма;
- первоначальная сумма;
D = S – P - дисконт.
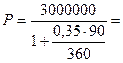 2 758 620,69 руб.
2 758 620,69 руб.
D = 3 000 000 – 2 758 620,69 = 241 379,31 руб.
3
Через 9 дней
предприятие должно получить по векселю 3 000 000 руб. Банк приобрел этот
вексель с дисконтом. Банк учел вексель по учетной ставке 35% годовых (год равен
360 дням). Определить полученную предприятием сумму и дисконт.
Решение:
D = S·n·d - дисконт;
P = S – D - полученная сумма.
D = 3 000 000 · 0.35 · 90 / 360 = 262 500 руб.
P = S – D = 3 000 000 – 262 500 = 2 737 500 руб.
4
В кредитном
договоре на сумму 3 000 000 руб. и сроком 5 года, зафиксирована
ставка сложных процентов, равная 35% годовых. Определить наращенную сумму.
Решение:
S = P(1+i)n
S = 3 000 000 · (1 + 0.35)5 = 13 452
099 руб.
5
Ссуда, размером 3 000 000
руб. предоставлена на 5 года. Проценты сложные, ставка – 35% годовых. Проценты
начисляются 4 раза в год. Вычислить наращенную сумму.
Решение:
S = P(1+j/m)N
Число периодов начисления в году m=4
S = 3 000 000
· (1+0,35 / 4)20 = 16 058 552 руб.
6
Вычислить
эффективную ставку процента, если банк начисляет проценты 4 раза в году, исходя
из номинальной ставки 35% годовых.
Решение:
iэ = (1+j/m)m – 1
Эффективная ставка показывает, какая годовая ставка
сложных процентов дает тот же финансовый результат, что и m-разовое наращение в год по ставке j/m.
iэ = (1+0,35/4)4 – 1 = 0,3986 или 39,86%
7
Определить, какой
должна быть номинальная ставка при начислении процентов 4 раза в году, чтобы
обеспечить эффективную ставку 35% годовых.
Решение:
j = m[( 1+iэ )1/m – 1]
j = 4·[( 1+0.35)1/4
– 1] = 0,3116 т.е. 31,16%
8
Через 5 лет
предприятию будет выплачена сумма 3 000 000 руб. Определить ее
современную стоимость при условии, что применяется сложная процентная ставка 35%
годовых.
Решение:
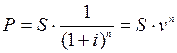
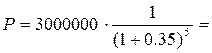 669 040,5 руб.
669 040,5 руб.
9
Через 5 года по
векселю должна быть выплачена сумма 3 000 000 руб. Банк учел вексель
по сложной учетной ставке 35% годовых. Определить дисконт.
Решение:
P = S(1 - dсл)n
где dсл – сложная годовая учетная ставка
P = 3 000 000 · (1 – 0,35)5 = 348
087 руб.
D = S – P = 3 000 000 – 348 087 = 2 651
913 руб.
10 В течение 5 лет на расчетный счет в конце каждого года
поступает по 3 000 000, на которые 4
раза в году начисляются проценты по сложной годовой ставке 35%. Определить
сумму на расчетном счете к концу указанного срока.
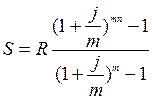
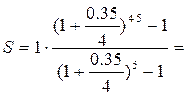 25 061 522 млн. руб.
25 061 522 млн. руб.