ГЛАВА 2. ФОРМИРОВАНИЕ ИНВЕСТИЦИОННОГО ПОРТФЕЛЯ
ФИЗИЧЕСКОГО ЛИЦА
2.1. Критерии эффективности финансовых инструментов. Критерии
оптимальности инвестиционного портфеля
Вложения юридических и физических лиц в ценные бумаги требуют
эффективного управления. В этой связи существует понятие управления портфелем
ценных бумаг.
В сложившейся мировой практике фондового рынка под
инвестиционным портфелем понимается некая совокупность ценных бумаг,
принадлежащих физическому или юридическому лицу, выступающая как целостный
объект управления. Смысл портфеля – улучшить условия инвестирования, придав
совокупности ценных бумаг такие инвестиционные характеристики, которые
недостижимы с позиции отдельно взятой ценной бумаги и возможны только при их
комбинации. [2, с.329]
При формировании портфеля возможны три основные формулировки задачи
оптимизации[4,с. 65]:
1.
целевая функция — доходность;
2.
целевая функция — надежность;
3.
двухмерная оптимизация по параметрам «надежность‑доходность»
с последующим исследованием оптимального по Парето множества решений.
Решение оптимизационной задачи в последней формулировке позволяет найти
не одну точку (оптимальную структуру портфеля), а множество оптимальных точек
на плоскости критериев, т. е. оптимальное множество Парето, и уже в этом
множестве выбрать критерий, наиболее важный для конкретного случая.
Портфель, формируемый инвестором, состоит из
нескольких активов, каждый из которых имеет свою ожидаемую доходность. Указанная
ожидаемая доходность по каждому отдельному активу определяется следующим
образом. Сначала рассматриваются вероятности получения дохода и определяются
на основании анализа данных фондового рынка их значения. Например, рассмотрим
вариант, состоящий из возможного диапазона колебания доходности акций от
минимального значения 10% до максимального 24% вероятности граничных и
промежуточных значений в таблице 1.
Таблица 1
Диапазон колебаний доходности акций
|
Доходность,
%
|
10
|
13
|
18
|
24
|
|
|
Вероятность,
%
|
30
|
35
|
20
|
15
|
Итого:
100
|
Ожидаемая доходность конкретного актива определяется как средняя
арифметическая, где весами выступают вероятности каждого исхода события. В
рассматриваемом примере ожидаемая доходность акции составит: 10% * 0,30 + 13%
* 0,35 + 18% * 0,20 + 24% * 0,15= 14,75%.
Ожидаемая доходность портфеля dп рассчитывается как средневзвешенная величина
ожидаемых доходностей входящих в него различных активов, т.е. она
рассчитывается по выражению:
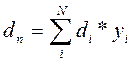(1)
где di
– ожидаемая доходность по i-му
активу; yi –
удельный вес стоимости i-го
актива в общей стоимости всех активов, входящих в портфель. [12, с.195]
Например, портфель состоит из двух пакетов акций стоимостью 3000 руб. и
2000 руб. Ожидаемая доходность по первому пакету составляет 12%, а по второму —
16%. Доля первого пакета в портфеле составляет 3000 / (3000 + 2000) = 0,6 , а
доля второго 2000 / (3000 + 2000) = 0,4. В данном примере ожидаемая
доходность портфеля в целом составит: 12% * 0,6 + 16% * 0,4 = 13,6%.
При покупке какого-либо актива инвестор учитывает не только значение
ожидаемой его доходности, но и уровень его риска. Рассчитанная изложенным выше
способом ожидаемая доходность выступает как средняя ее величина в соответствии
с имевшей место динамикой актива на фондовом рынке. Но на практике фактическая
доходность, как правило, будет отличной от рассчитанной ожидаемой. То есть
всегда имеется степень риска получить доходность ниже ожидаемой (если окажется
выше, то это не риск, а “приварок”). В практике управления портфелями ценных
бумаг в качестве способа расчета величины риска используют показатели
дисперсии и стандартного отклонения показателя фактической доходности от величины
расчетной ожидаемой доходности. Указанные показатели учитывают отклонения
фактической доходности от ожидаемой, как в сторону уменьшения, так и в сторону
увеличения. Графическая интерпретация полученных результатов отражена на рис. 1
(приложение 1)
Величина дисперсии актива s2 рассчитывается по формуле:
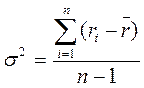(2)
где 
- средняя доходность
актива;
ri – доходность актива в i-ом периоде;
n – число периодов наблюдения. [12,
с.196]
Средняя доходность актива определяется как средняя арифметическая
доходностей актива за периоды наблюдения по выражению:
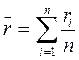(3)
Стандартное отклонение доходности активов s определяется как корень
квадратный из дисперсии. [12, с.196]
К примеру, доходность актива за пять лет составила: 1-й год — 20%, 2-й
год —25%, 3-й год — 22%, 4-й год — 19%, 5-й год — 14%. Средняя доходность
актива за пять лет составит: (20+25+22+19+14)/5=20%.
Отклонения величины доходности по годам от средней доходности будут
равны: 20 – 20 = 0%; 25 – 20 = 5; 22 – 20 = 2; 19 – 20 = 1; 14 – 20 = 6%.
Сумма квадратов полученных отклонений составит: 02 + 52
+ 22 + (-1)2 + (-6)2 = 66.
Дисперсия будет равна 66/4 = 16,5; а стандартное отклонение 
%.
Стандартное отклонение характеризует величину и вероятность отклонения
доходности актива от ее средней величины за определенный период. В
рассмотренном примере отклонение доходности актива за год составляет 4,06%.
Ожидаемый риск портфеля ценных бумаг зависит от сочетания стандартных
отклонений (дисперсий) активов, входящих в его состав. Но его нельзя определять
как средневзвешенную величину указанных стандартных отклонений, так как часть
значений отклонений будет взаимно погашаться и фактический риск портфеля будет
меньше. Поэтому для определения степени взаимосвязи и направления изменения
доходностей двух активов используют такие показатели математической статистики,
как ковариация и коэффициент корреляции.
Показатель ковариации определяется по формуле:
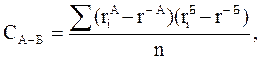(4)
где СА-Б – ковариация доходности активов А и Б;
, 
- доходность активов А
и Б в i-ом периоде;
, 
– средняя доходность
активов А и Б за n
периодов;
n – число периодов, за которые
рассматривалась доходность активов А
и Б. [12, с.197]
Положительное значение ковариации говорит о том, что доходность активов
изменяется в одном направлении, а отрицательное – в разных направлениях.
Нулевое значение ковариации означает, что взаимосвязи между доходностями
активов нет.
Другим применяемым показателем степени взаимосвязи изменения доходностей
двух активов является коэффициент корреляции, рассчитываемый по формуле:
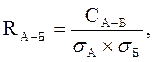(5)
где СА-Б – ковариация доходности активов А и Б;
sА , sБ
– стандартные отклонения доходности активов А и Б. [12, стр.198]
Риск (дисперсия) портфеля, состоящего из нескольких активов, 
рассчитывается по
формуле:
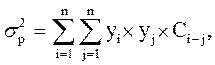(6)
где Сi-j – ковариация
доходности активов, входящих в портфель;
yi ,yj – удельные веса активов в
общей стоимости портфеля. [12, стр.199]
Знак двойной суммы в этой формуле означает, что при вычислениях дисперсии
сначала для расчета величины yi yj Ci-j удельный вес первого
актива yi
умножается на произведение yj Ci-j для всех видов
активов, затем берется удельный вес второго актива и умножается на то же
произведение для всех активов, начиная с первого. Указанные произведения
суммируются и таким образом находится значение дисперсии по совокупности
активов, входящих в портфель.
Практика показывает, что с увеличением количества видов ценных бумаг в
портфеле уменьшается риск инвестиций. Это происходит потому, что в портфель
включаются ценные бумаги, слабокоррелированные между собой, только в этом
случае возможно снижение риска. Процедура включения в портфель различных видов
ценных бумаг, имеющих низкий коэффициент корреляции, называется диверсификацией.
При диверсификации риск портфеля снижается только до определенного
уровня, ниже которого путем диверсификации риск уменьшить нельзя. Таким
образом, риск представляет собой сумму диверсифицируемого и
недиверсифицируемого рисков. Диверсифицируемая часть риска представляет собой
несистематический риск, а недиверсифицируемая – систематический.
Несистематический риск определяется факторами, связанными с деятельностью
предприятия-эмитента и изменениями рыночной конъюнктуры. Систематический риск
определяется глобальными обстоятельствами не зависящими от инвестора и
эмитента. К таким обстоятельствам можно отнести политические события на уровне
страны и на международном уровне, изменения законодательства, экономические
реформы и т.п.
Можно составить безрисковый портфель, но отсутствие риска для него будет
означать отсутствие только несистематического риска, систематический риск
останется. К примеру, в российских условиях безрисковым портфелем является
портфель в иностранной валюте (долларах США), но и он подвержен систематическому
риску, связанному, например, с возможными изменениями законодательства, касающимися
ограничений обращения иностранной валюты на территории России. [3, с.165]
Данная задача заключается в том, чтобы из трех активов составить такой
портфель, который обеспечивал бы инвестору минимальный риск при требуемой
доходности. Для этой цели необходимо определить количество каждого из активов
моделируемого портфеля ценных бумаг.
Составим таблицу доходности активов по периодам в таблице 2 (приложение 2).
Количество
периодов выберем равным 22, т.к. количество объясняющих переменных должно быть
в 5-6 раз больше объясняемых. В принципе, чем объясняющих переменных больше,
тем точнее будут произведены расчеты.
Эту таблицу должен заполнить инвестор по статистическим данным и она
будет являться исходными данными.
Таблица 3
|
актив
А
|
актив
Б
|
актив
С
|
|
|
|
|
|
средняя
доходность %
|
31,18
|
25,14
|
33,82
|
|
дисперсия
|
14,16
|
1,84
|
24,63
|
|
стандартное
отклонение
|
3,76
|
1,36
|
4,96
|
|
ожидаемая
доходность %
|
31,18
|
25,14
|
33,82
|
|
ковариация
|
актив
А
|
актив
Б
|
актив
С
|
|
актив
А
|
|
-2,84
|
10,81
|
|
актив
Б
|
-2,84
|
|
-3,43
|
|
актив
С
|
10,81
|
-3,43
|
|
Таблица 4
В качестве ожидаемой доходности актива возьмем среднее значение
доходности этого актива.
Таблица 5
|
Требуемая доходность портфеля, %
|
31
|
|
Риск портфеля, %
|
8,59
|
|
Ожидаемая доходность портфеля, %
|
31
|
Еще одним значением, которое необходимо ввести инвестору будет требуемая
доходность портфеля ценных бумаг (табл. 5).
Инвестор вводит такое значение требуемой доходности, для которого ему
требуется минимизировать риск портфеля ценных бумаг.
Решением данной задачи служит удельный вес каждого из активов в портфеле
ценных бумаг, при котором достигается минимальный риск, причем ожидаемая
доходность должна быть не меньше требуемой.
Довольно часто в инвестиционной практике возникает потребность в
сравнении проектов различной продолжительности[5,с . 188].
Пусть проекты А и Б рассчитаны соответственно на i и j лет. В этом случае рекомендуется:
·
найти наименьшее общее кратное сроков действия
проектов - N;
·
рассматривая каждый из проектов как
повторяющийся, рассчитать с учетом фактора времени суммарный NPV проектов А и
В, реализуемых необходимое число раз в течение периода N;
·
выбрать тот проект из исходных, для которого
суммарный NPV повторяющегося потока имеет наибольшее значение.
Суммарный NPV повторяющегося потока находится по формуле:
1 1 1 1
NPV (i, n) = NPV(i) (1 +
——— + ——— + ——— +...+————), (7)
(1+r)i (1+r)2i (1+r)3i (1+r)N-i
где NPV (i) - чистый приведенный доход исходного
проекта;
i-
продолжительность этого проекта;
r - коэффициент дисконтирования в долях единицы;
N - наименьшее общее кратное;
n - число повторений исходного проекта (оно характеризует число слагаемых
в скобках).
Таблица 6
|
удельный
вес
|
актив
А
|
актив
Б
|
актив
С
|
|
0,340
|
0,221
|
0,438
|
Пример 1
В каждой из двух приведенных ниже ситуаций требуется выбрать наиболее
предпочтительный проект в составе портфеля (в млн руб.), если цена капитала
составляет 10%:
а) проект А: -100, 50, 70; проект В: -100, 30,
40, 60;
б) проект С: -100, 50, 72; проект В: -100, 30,
40, 60.
Если рассчитать NPV для проектов А, В и С, то они составят
соответственно: 3,30 млн руб., 5,4 млн руб., 4,96 млн руб. Непосредственному
сравнению эти данные не поддаются, поэтому необходимо рассчитать NPV
приведенных потоков. В обоих вариантах наименьшее общее кратное равно 6. В
течение этого периода проекты А и С могут быть повторены трижды, а проект В -
дважды.
В случае трехкратного повторения проекта А суммарный NPV равен 8,28 млн
руб.:
NPV = 3,30 + 3,30 / (1+0,1)2+3,30 / (1+0,1)4 = 3,30
+ 2,73 +2,25 = 8,28,
где 3,30 - приведенный доход 1-ой реализации проекта А;
2,73 - приведенный доход 2-ой реализации проекта А;
2,25 - приведенный доход 3-ей реализации проекта А.
Поскольку суммарный NPV в случае двукратной реализации проекта В больше
(9,46 млн руб.), проект В является предпочтительным.
Если сделать аналогичные расчеты для варианта (б), получим, что суммарный
NPV в случае трехкратного повторения проекта С составит 12,45 млн руб. (4,96 +
4,10 + 3,39). Таким образом, в этом варианте предпочтительным является проект
С.
Метод бесконечного цепного повтора
сравниваемых проектов
Рассмотренную выше методику можно упростить в вычислительном плане. Так,
если анализируется несколько проектов, существенно различающихся по
продолжительности реализации, расчеты могут быть достаточно сложными. Их можно
упростить, если предположить, что каждый из анализируемых проектов может быть
реализован неограниченное число раз. В этом случае n®¥ число слагаемых в
формуле расчета NPV(i, n) будет стремиться
к бесконечности, а значение NPV(i, ¥) может быть найдено
по формуле для бесконечно убывающей геометрической прогрессии:
(1+r)i
NPV(i, ¥)= lim NPV(i, n) = NPV(i) ————. (7)
n®¥ (1+r)i-1
Из двух сравниваемых проектов проект, имеющий большее значение NPV(i, ¥),
является предпочтительным.
Так, для рассмотренного выше примера:
вариант а):
проект А: i = 2,
поэтому
NPV(2, ¥)
= 3,3 (1+0,1)2/((1+0,1)2-1) = 3,3×5,76
= 19,01 млн руб.;
проект В: i = 3,
поэтому
NPV(3, ¥)
= 5,4 (1+0,1)3/((1+0,1)3-1) = 5,4×4,02=21,71
млн руб.;
вариант б):
проект В: NPV(3, ¥) = 21,71 млн руб.,
проект С: NPV(2, ¥) = 28,57 млн руб.
Таким образом, получены те же самые результаты: в варианте а)
предпочтительнее проект В; в варианте б) предпочтительнее проект С.
Далее рассмотрим основные критерии
формирования инвестиционного портфеля из
долговых обязательств.
Предположим, что доходности долговых бумаг являются случайными
процессами, в сечении которых лежат нормально распределенные случайные
величины. В этом случае на классе долговых обязательств можно ставить и решать
задачу оптимизации по Марковицу [2, с.177]. Продемонстрируем это на примере из
двух бумаг - дисконтной и процентной.
Пример оптимизации bond-портфеля
Пусть в момент TI = 0 выпущено две облигации – А
и В – с равным сроком обращения TМ - TI = 3
(здесь и далее параметры времени - в годах). Также бумаги А и В характеризуются
следующими параметрами выпуска:
А:
·
тип бумаги – дисконтная;
·
номинал бумаги N1 =
$2,000;
·
размер дисконта при выпуске – (N1-
N01) / N1 = 30%.
В:
·
тип бумаги – процентная;
·
номинал бумаги N2 =
$1,000;
·
размер дисконта при выпуске – (N2-
N02) / N2 = 10%;
·
размер процента – N2 /
N2 = 15% годовых;
·
число процентных выплат К2
= 3 c частотой 1 раз в год.
Время принятия решения о формировании портфеля t = 1+0,
плановый срок владения портфелем T = 1.5. Поэтому доходности и
риски измеряются на момент времени t + T = 2.5.
Не прибегая к статистическому анализу шумов курсовых цен и их взаимной
корреляции, заложим расчетные значения СКО шумов цен бумаг А и В, причем эти
шумы считаем приведенными к стационарному виду по правилам, изложенным нами в
предыдущем сообщении:
01 = 02 =
0 (8)
Также предположим что совместный статистический анализ нормализованных
шумов случайных процессов доходностей бумаг А и В дает нам значение коэффициента
корреляции r12. Тогда ковариационная матрица
доходностей на интервале t [1,3] имеет вид
(9)
Задача состоит в том, чтобы исследовать свойства портфеля из бумаг А и В
и найти такую их пропорцию, которая оптимизирует портфель в точке (t + T).
Решение задачи
1. Справедливая цена дисконтной бумаги А определяется соотношением
(10)
где 
(11)
СКО шума цены бумаги А определяется по формуле
(12)
Среднеожидаемая доходность по бумаге за плановый период владения имеет
вид
(13)
где C1(t) определяется по (3), а СКО случайной
величины доходности бумаги А
(14)
где H1(t) – известное значение покупной цены
бумаги А в момент времени t.
2. Справедливая цена дисконтной бумаги В определяется соотношением
,если 
;
, если 
;
, если 
, (15)
а внутренняя норма доходности долгового инструмента r2
отыскивается как корень трансцендентного уравнения вида
, (16)
а решение уравнения дает
r2 = 0.540. (17)
Замечание. Здесь и далее договоримся, что купонный платеж производится в
моменты времени, строго равные расчетным. Непосредственно сразу после платежа
(в момент t + 0) справедливая цена бумаги падает ровно на размер
купона, поэтому левые ограничения по переменной t выполняются как
строгие неравенства. То есть мы определяем функцию как непрерывную слева.
СКО шума цены бумаги B определяется по формуле
, если 
;
, если ;
, если 
. (18)
Среднеожидаемая доходность по бумаге за плановый период владения имеет
вид
(19)
где m – число купонных платежей в интервале времени [t,
t+T ];
C2(t) определяется по формуле (16), а СКО случайной величины доходности
бумаги В
(20)
где H2(t) – известное значение покупной цены
бумаги В в момент времени t.
3. Тогда показатели среднеожидаемой доходности и риска портфеля имеют
выражения
(21)
(22)
где х1 и х2 -
соответственно доли бумаг А и В в объединенном портфеле, и выполняется
х1 + х2 = 1. (23)
4. Произведем упрощение формул, подставив в них значения t
= 1, T = 1.5:
; (24)
; (25)
; (26)
; (27)
Для упрощения, не влияющего на ход наших рассуждений, мы полагаем H1(1)
= C1(1), H2(1) = C2(1). Тогда
; (28)
; (29)
; (30)
; (31)
; (32)
(33)
; (34)
; (35)
При х1 = 0
;
.
А при х1 = 1
= 
= 0.130,
= 
=
.
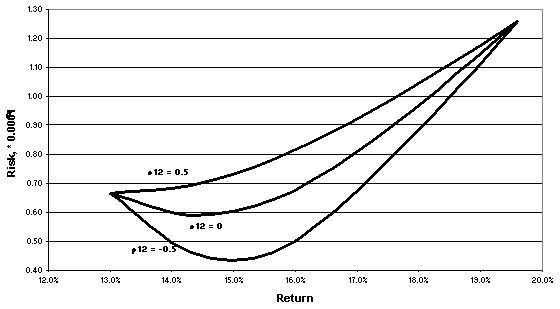
Рис. 2. Эффективные границы портфелей из бумаг А и В
На рис. 2 представлены эффективные границы портфелей из бумаг А и В, где
вариантой выступает коэффициент корреляции r12. Видно,
что при отрицательной корреляции бумаг на эффективной границе есть участок, где
падение риска портфеля сопровождается ростом его доходности, и есть безусловный
оптимум соотношения «доходность - риск». А задача Марковица, решаемая для
двумерного случая, вырождается в поиск ординаты эффективной границы,
соответствующей фиксированной абсциссе (выбор максимума доходности при заданном
уровне риска или минимума риска при заданной доходности).
2.2. Формирование модельного инвестиционного портфеля
Выбор
модельных классов и их индексирование
Коснемся российской специфики
анализа фондового рынка в г. Новосибирске.
Десять лет существования рынка ценных бумаг – это, конечно, ничтожный срок, как с точки зрения
формирования рынка, так и с точки зрения анализа статистики этого рынка. Однако
более пристальное рассмотрение показывает, что российский рынок ценных бумаг, еще
не успев зародиться, попал в водоворот мирового финансового кризиса.
Сегодня мы можем говорить о пяти
модельных классах российских ценных бумаг, куда в основном направляются
фондовые инвестиции:
·
Государственные ценные бумаги и облигации
субъектов РФ;
·
Обязательства субъектов РФ (в основном эмиссии
Москвы и Санкт-Петербурга);
·
Корпоративные облигации и векселя;
·
Акции десятка наиболее продвинутых компаний
(«голубых фишек» местного значения).
·
Корпоративные акции второго эшелона.
Постепенно оживает торговля фьючерсами и опционами
на акции, однако инвестиции в производные ценные бумаги мы здесь не
рассматриваем как модельные. Также мы не рассматриваем в качестве фондовых
инвестиции в мультивалютные портфели и в депозитные сертификаты банков, хотя в
портфелях инвесторов эти инструменты могут присутствовать наряду с
перечисленными выше фондовыми активами.
Только-только начинают появляться
публичные индексы для ценных бумаг с фиксированным доходом. В качестве индекса
корпоративных акций первого эшелона можно рассматривать индексы РТС (валютный и
технический), индекс ММВБ-10, а также композитный индекс РБК - с поправкой на то, что акции РАО
«Газпром» не входят в оценку индексов РТС и ММВБ. А что до акций второго
эшелона, то объем торгов по ним незначителен, и должного внимания этому
сегменту рынка (его индексированию, к примеру) не уделяется (хотя в целях
полноты изложения следует упомянуть индекс агентства AK&M).
Пытаясь преодолеть недостаточность в информационном обеспечении
российского фондового рынка, по результатам договорного взаимодействия с
Пенсионным Фондом РФ компания Siemens Business Services выработала и поставила
в рамках своего программного продукта «Система оптимизации фондового портфеля»
более 20 индексов, описывающих поведение соответствующего числа модельных
классов (таблица 8, приложение 3).
Комментарий. В наименовании индексов составляющая RUB
отражает тот факт, что все используемые индексы имеют размерность российский
рубль, т.е. выражают стоимость российских денег, вложенных в те или иные
фондовые активы или валюту. Составляющая Cum говорит о том, что исходные
индексы, имеющие процентный вид текущей доходности вложений, приведены по
формуле кумулятивного дохода к S-виду, имеющему вид не доходности
актива, а его цены.
Нечетко-множественная
оптимизация модельного портфеля
Исторически первым методом оптимизации фондового портфеля был метод,
предложенный Марковицем. Суть его в следующем.
Пусть портфель содержит N типов ценных бумаг (ЦБ), каждая из которых
характеризуется пятью параметрами:
·
начальной ценой Wi0 одной бумаги
перед помещением ее в портфель;
·
числом бумаг ni в портфеле;
·
начальными инвестициями Si0 в данный
портфельный сегмент
Si0 = Wi0 ´ ni; (36)
Из перечисленных условий ясно, что случайная величина доходности бумаги
имеет нормальное распределение с первым начальным моментом ri и вторым
центральным моментом si. Это распределение не обязательно должно
быть нормальным, но из условий винеровского случайного процесса нормальность
вытекает автоматически.
Сам портфель характеризуется:
·
суммарным объемом портфельных инвестиций S;
·
долевым ценовым распределением бумаг в портфеле
{xi}, причем для исходного портфеля выполняется
; (37)
·
корреляционной матрицей {rij},
коэффициенты которой характеризуют связь между доходностями i-ой и j-ой бумаг.
Если rij
= -1, то это означает полную отрицательную корреляцию, если rij
= 1 - имеет место полно положительная корреляция. Всегда выполняется rii
= 1, так как ценная бумага полно положительно коррелирует сама с собой.
Таким образом, портфель описан системой статистически связанных случайных
величин с нормальными законами распределения. Тогда, согласно теории случайных
величин, ожидаемая доходность портфеля r находится по формуле
, (38)
а стандартное отклонение портфеля s -
. (39)
Задача управления таким портфелем имеет следующее описание: определить
вектор {xi}, максимизирующий целевую функцию r вида (38) при
заданном ограничении на уровень риска s, оцениваемый (39):
=const £ sM, (40)
где sM
– риск бумаги с максимальной среднеожидаемой доходностью. Запись (40)
есть не что иное, как классическая задача квадратичной оптимизации, которая
может решаться любыми известными вычислительными методами.
Замечание. В подходе Марковица
к портфельному выбору под риском понимается не риск неэффективности инвестиций,
а степень колеблемости ожидаемого дохода по портфелю, причем как в меньшую, так
и в большую сторону. Можно без труда перейти от задачи вида (14) к задаче, где
в качестве ограничения вместо фиксированного стандартного отклонения выступает
вероятность того, что портфельная доходность окажется ниже заранее
обусловленного уровня.
Если задаваться различным уровнем ограничений по s, решая задачу
(14), то можно получить зависимость максимальной доходности от s вида
rmax =
rmax (s) (41)
Выражение (41), именуемое эффективной
границей портфельного множества, в координатах «риск-доходность» является
кусочно-параболической вогнутой функцией без разрывов. Правой точкой границы
является точка, соответствующая тому случаю, когда в портфеле оказывается одна
бумага с максимальной среднеожидаемой доходностью.
Подход Марковица, получивший широчайшее распространение в практике
управления портфелями, тем не менее имеет ряд модельных допущений, плохо
согласованных с реальностью описываемого объекта - фондового рынка. Прежде
всего это отсутствие стационарности ценовых процессов, что не позволяет
описывать доходность бумаги случайной величиной с известными параметрами. То же
относится и корреляции.
Если же мы рассматриваем портфель из модельных классов, а ценовую
предысторию индексов модельных классов - как квазистатистику, то нам следует
моделировать эту квазистатистику многомерным нечетко-вероятностным распределением
с параметрами в форме нечетких чисел. Тогда условия записываются в нечетко-множественной форме, и задача квадратичной
оптимизации также решается в этой форме. Решением задачи является эффективная
граница в виде нечеткой функции полосового вида.
Каждому отрезку на эффективной границе, отвечающей абсциссе портфельного
риска, соответствует нечеткий вектор оптимальных портфельных долей.
И, наконец, если нам заданы контрольные нормативы по доходности и риску
(бенчмарк модельного портфеля), которые нам следует соблюсти в нашем портфеле,
увеличивая доходность и одновременно снижая риск. Если бенчмарк попадает в
полосу эффективной границы, то возникает дабл-риск (по факторам доходности и
волатильности), что модельный портфель «не переиграет» бенчмарк.
Рассмотрим простейший пример американского модельного портфеля из двух
модельных классов: правительственных долгосрочных облигаций (Класс 1, характеризующийся индексом LB
Govt Bond) и высококапитализированных акций (Класс 2, характеризующийся индексом S&P500). Сводные данные по
обоим индексам приведены в таблице 8.
Таблица 8
Исходные данные по модельным классам
|
Номер модельного
класса
|
Ожидаемая
доходность r1,2 ,
% год
|
Ожидаемая
волатильность s1,2,
% год
|
|
мин
|
средн
|
макс
|
мин
|
средн
|
макс
|
|
1 Облигации
|
6.0
|
6.1
|
6.2
|
0.6
|
0.7
|
0.8
|
|
2 Акции
|
10
|
12.5
|
15
|
20
|
25
|
30
|
Нам следовало бы еще оценить корреляцию двух индексов. Но, как я покажу
далее, в нашем случае этого не потребуется. Пока же для общности обозначим коэффициент корреляции r12.
Надо сразу оговориться, что случай портфеля из двух компонент является вырожденным с точки зрения оптимизации.
Здесь полное множество портфельных решений представляет собой участок в общем
случае кривой линии на плоскости, и он же является эффективной границей. Так
что в настоящем примере мы не сколько решаем оптимизационную задачу, сколько
ищем аналитический вид эффективной границы в координатах «риск-доходность».
Запишем формулы, представленные выше в
частном виде
(42)
(43)
x2 = 1- x1 (44)
Все «постоянные» коэффициенты в (42) - (44) являются треугольными
нечеткими числами. Можно было бы как-то отличить треугольные параметры от
обычных скалярных, вводя специальную запись, но, честно говоря, мне не хочется
загромождать формулы. И, поскольку в нашем случае s2 >> s1,
то имеет место приближенное равенство:
, (45)
и справедливо
- (46)
уравнение эффективной границы в виде полосы с прямолинейными границами
(см. рис. 3).
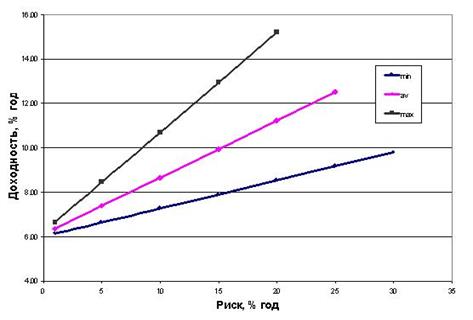
Рис. 3. Эффективная граница в виде полосы с линейными границами
Коэффициент пропорциональности в есть не что иное, как хорошо известный в
портфельном менеджменте показатель Шарпа
– отношение доходности индекса (за вычетом безрисковой составляющей
доходности) к волатильности индекса. Только в нашем случае он имеет нечеткий
вид, сводимый к треугольному по правилу:
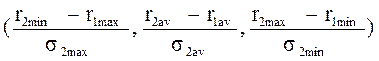(47)
В таблицу 9 сведены границы для модельного класса
облигаций в структуре модельного портфеля для различных уровней риска. По краям
полосы разброс портфельных границ ниже, чем в середине. Это объясняется тем,
что на краях полосы эффективной границы портфель обладает вполне определенным
стилем: большей доходности отвечает модельный класс акций, а меньшему риску –
модельный класс облигаций.
Таблица 9
Оптимальная
доля облигаций в портфеле
|
Риск портфеля, % год
|
1
|
5
|
10
|
15
|
20
|
25
|
30
|
|
Доля облигаций в портфеле
|
max
|
0.967
|
0.833
|
0.667
|
0.500
|
0.333
|
0.167
|
0.000
|
|
av
|
0.960
|
0.800
|
0.600
|
0.400
|
0.200
|
0.000
|
0
|
|
min
|
0.950
|
0.750
|
0.500
|
0.250
|
0.000
|
0
|
0
|
|
Разброс
|
0.067
|
0.083
|
0.167
|
0.250
|
0.333
|
0.167
|
0
|
Бенчмарк-риск
Инвестор, вкладывая деньги, всегда ставит перед собой определенную
инвестиционную цель (например, накопить денег на обучение детей). Процесс
такого накопления долгосрочен и требует поэтапного контроля доходности
инвестиций. Например, инвестор поставил своей целью иметь доход не хуже 8%
годовых с риском не хуже 10%. Это и есть бенчмарк.
Поглядев на эффективную границу и заглянув в таблицу 9, инвестор
формирует модельный портфель, заполняя его на 50% - 60% облигациями. Он ожидает
разброс доходности, оцениваемый (20), от 7.27% до 10.7% годовых. Нижняя граница
разброса лежит ниже бенчмарка, - значит, существуют ненулевые шансы не
выполнить инвестиционный план.
Каковы эти шансы? На этот вопрос дает ответ метод Недосекина-Воронова из [1, с. 154], где риск срыва плана
(применительно к нашему случаю) оценивается формулой
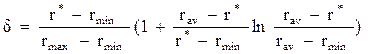, (48)
где r*=8% - бенчмарк, (rmin = 7.27%, rav
= 8.66%, rmax = 10.70%) – параметры треугольного числа ожидаемой
доходности модельного портфеля. И расчеты по (48) дают d = 19.3%. Много это или
мало? Все зависит от предпочтений инвестора. Возможно, ему покажется, что риск
велик, и он сочтет свой финансовый план чрезмерно напряженным. В то же время
надо обратить внимание на то, что бенчмарк ниже ожидаемого среднего, поэтому
шансы на исполнение планов весьма велики.
Наполнение
модельного портфеля реальными активами
Когда оптимальные доли компонент модельного портфеля определены,
необходимо выполнить процедуру наполнения компонент модельного портфеля
реальными активами. Как показывает практика фондовых инвестиций, ценовое
поведение реальных активов в структуре модельного класса характеризуется
эффектом синхронной волатильности, когда цены большинства реальных активов в
рамках класса движутся в одну сторону. Эта практически полная корреляция
активов делает бессмысленной оптимизацию реального портфеля по Марковицу. К
тому же для такой оптимизации невозможно получить достоверные исходные данные
по ожидаемой доходности и риску.
Возможно провести оптимизацию реального портфеля по
альтернативному принципу, отталкиваясь от инвестиционного качества реальных
активов, входящих в портфель. Тогда можно воспользоваться комплексными оценками
инвестиционного качества, полученными в рамках рейтинга облигаций и скоринга
акций с использованием нечетко-множественных описаний [2, с. 179]. Чем выше
уровень качества актива, тем больший вес он имеет право занять в рамках
выделенной группы активов реального портфеля. Можно определять оптимальную долю
актива двумя способами:
- на пропорциональной основе, как отношение комплексного показателя к
сумме комплексных показателей активов портфеля;
- по принципу Фишберна. Если уровни привлекательности N активов
проранжировать по убыванию, то соответствующие веса компонент портфеля также
расположатся по убыванию, а их веса в портфеле можно оценить по схеме Фишберна:
. (49)
Приведем краткое изложение метода скоринга акций на примере
технологического сектора акций в г .
Новосибирске [8, с. 19]. Прежде всего построим классификатор уровней по
набору выбранных показателей для комплексной оценки инвестиционной
привлекательности акций (табл. 10, приложение 3), применительно к экономическим
условиям Новосибирска в 2004 году:
Ранжируя выбранные пять факторов (соотношение цена-доход P/E, капитализация Cap, доходность
собственного капитала ROE, коэффициент финансовой автономии D/E и коэффициент
переоценки активов P/B) по значимости для комплексной оценки, мы приходим к
системе предпочтений вида:
P/E ý Cap ý ROE = D/E = P/B, (50)
что приводит к выбору весов показателей в комплексной оценке по Фишберну:
p1 = 
p2 = 
p3 = p4 = p5 = 
(51)
Тогда, по аналогии с тем, как это сделано в [1, с.
172], получим комплексный показатель A_N для каждой бумаги методом двойной
свертки:
, (52)
где i – индекс отдельного показателя для их общего числа N=5, j – индекс
уровня показателя для общего числа уровней M=5, lij – ранг i-го
показателя по своему j-ому уровню,
определяемый функциями принадлежности соответствующих трапезоидных нечетких
чисел (абсциссы их вершин определяются
таблицей 1),
- (53)
это абсциссы максимумов функций принадлежности терм-множества
лингвистической переменной «Оценка бумаги». Тогда среднеожидаемый ранг
j-го уровня, взвешенный по всем N показателям,
оценивается формулой
, (54)
и справедливо
. (55)
Получив оценку A_N, мы можем произвести ее распознавание по таблице 11
(приложение 4)
Агрегированным результатом нашего скоринга является сводная таблица 12.
Таблица 12
Результаты скоринга сектора Technology
|
Факторы
|
Распределение
факторов по уровням
|
|
ОН
|
Н
|
С
|
В
|
ОВ
|
|
Cap
|
33%
|
24%
|
25%
|
12%
|
6%
|
|
P/E
|
37%
|
22%
|
26%
|
12%
|
3%
|
|
ROE
|
13%
|
48%
|
27%
|
4%
|
7%
|
|
D/E
|
9%
|
16%
|
12%
|
10%
|
52%
|
|
P/B
|
16%
|
8%
|
19%
|
30%
|
27%
|
|
Summary
|
26%
|
23%
|
23%
|
13%
|
14%
|
Гистограмма результирующего фактора по отобранным корпорациям представлена
на рис. 4.
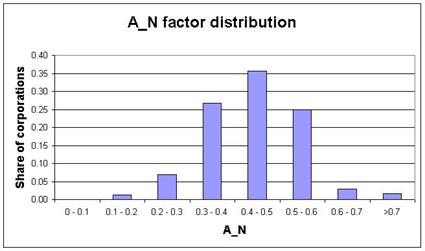
Рис. 4. Гистограмма для фактора A_N
Из полученных данных следует, что львиная доля предприятий группируется в
пределах 0.3 – 0.5 по фактору A_N, что характеризует инвестиционную
привлекательность сектора Technology как нечто промежуточное между низкой и
средней. Если точнее, то мы получили показатель A_N для сектора, равный 0.431.
Распознавание по таблице 8 дает: 80 к 20 за то, что значение фактора все же среднее.
Из этого, впрочем, не вытекает для сектора ничего хорошего. Выводы неутешительны:
Таблица 9 представляет собой нечто вроде фазового портрета сектора,
подобие карты. Из нее видно, какие проблемы для сектора являются ключевыми.
Во-первых, низкая прибыльность корпораций сектора, которая загоняет в «красный
угол» сразу два фактора: P/E и ROE. Во-вторых, свыше 50% корпораций сектора
обладают низкой капитализацией (менее 500 млн долл.), - а, следовательно,
возникает повышенный риск инвестиций в акции этих эмитентов (на фоне
продолжающейся рецессии экономики США). Правда, все карты может спутать
специфика военного времени. Если компании, работающие на войну, оживятся, то
это оживление по традиции почувствует весь рынок. Однако для мирных времен
такая картина может спровоцировать лишь одну реакцию – вывод капиталов.
2.3. Рекомендации по управлению инвестиционным
портфелем
Содержание управления портфелем ценных бумаг – это планирование, анализ и
регулирование состава портфеля, осуществление деятельности по его формированию
и поддержанию в целях достижения поставленных задач обеспечения его доходности,
эффективности при сохранении необходимого уровня ликвидности и минимизации
расходов на обслуживание. Портфель ценных бумаг является инструментом, с
помощью которого инвестору обеспечивается требуемая устойчивость дохода при
минимальном риске.
Наиболее важными параметрами планирования и контроля
в рамках управления портфелем ценных бумаг являются: доходность портфеля, риск
портфеля, определение стратегии в управлении портфелем.
Владея
инструментами определения доходности активов и портфеля ценных бумаг и
инструментами оценки степени риска формируемых портфелей, менеджер по
управлению ими осуществляет соответствующую стратегию.
В практике
управления менеджеры инвестиционных портфелей получают от их владельцев два
основных вида распоряжений. К первому виду распоряжений относятся распоряжения
обеспечить требуемый уровень ликвидности активов, среднюю надежную доходность
вкладываемых в ценные бумаги средств при допустимом риске. При этом могут
устанавливаться и сроки, на которые приобретаются бумаги. Примером таких
распоряжений могут быть распоряжения пенсионных фондов, страховых и т.п.
компаний, которым не принадлежат вкладываемые в ценные бумаги средства, или
которые имеют обязательства по своевременным выплатам и т.д. Ко второму виду
относятся распоряжения собственников средств обеспечить определенные параметры
по уровню доходности и риска размещения их в ценные бумаги.
В зависимости от
характера распоряжений по вложению средств в ценные бумаги и от характера
поведения менеджера на фондовом рынке выделяют две основные стратегии
управления портфелями ценных бумаг: пассивную и активную. [12, с.205]
При пассивной
стратегии портфель ценных бумаг более или менее постоянен. Менеджер портфеля
не ставит перед собой цель получить более высокую доходность по сравнению со
средней доходностью при допустимом уровне риска и исходит из того, что рынок
ценных бумаг эффективен, т.е. он обеспечивает малую колеблемость доходности
различных активов. В этом случае ценные бумаги покупаются на длительный период владения
ими, активно портфель не пересматривается. Его пересмотр производится только в
части тех активов, по которым имеется резкое и существенное ухудшение доходности,
снижение надежности получения стабильного регулярного дохода, устраивающего
инвестора.
Основной задачей менеджера инвестиционного портфеля при пассивной
стратегии управления им является снижение риска и обеспечение заданной
доходности. Если портфель состоит из небольшого числа активов, то он сохраняет
значительную степень диверсифицируемого риска. Чтобы его снизить применяется
стратегия, называемая копированием индекса. Суть ее состоит в том, что
формируемый портфель ценных бумаг должен иметь уровень доходности, близкий
индексу доходности по широкой базе ценных бумаг (копировать его), обращающихся
на фондовом рынке. Недостаток этой стратегии заключается в высоких трансактных
издержках по содержанию портфеля, поскольку в таком случае необходимо покупать
малое количество бумаг по большому количеству активов. Кроме того, при
включении дополнительного актива в портфель цена его падает, хотя включаемый
актив может быть и более доходным, чем портфель в целом. Другой прием
пассивного управления портфелем ценных бумаг состоит в его иммунизации. Суть
иммунизации заключается в формировании портфеля таким образом, чтобы его состав
соответствовал конъюнктуре. В случаях изменения процентных ставок по бумагам
потери (выигрыши) в стоимости облигаций будут компенсироваться соответственно
выигрышами (потерями) от реинвестирования купонов.
Активная стратегия проводится исходя из позиции владельцев и менеджеров
портфелей, что рынок не всегда является эффективным, что имеет место
существенная разница между доходностью различных активов. В связи с этим у
инвесторов появляется возможность за счет переоформления портфеля наращивать
его стоимость. Это осуществляется путем изменения пропорций видов финансовых
инструментов, включаемых в портфель (акции, облигации и др.) и варьирования категориями
активов внутри категорий финансовых инструментов (пропорциями в количестве
акций различных отраслей экономики, компаний, пропорциями между кратко-,
средне- и долгосрочными облигациями). В качестве инструмента выбора
приоритетных к приобретению бумаг используются и данные бета-коэффициентов по
активам. Если на фондовом рынке ожидается его оживление, подъем инвестиционной
активности, то целесообразно отдать предпочтение бумагам с более высокой
величиной указанного коэффициента. Если ожидается спад, то, наоборот – с
меньшей его величиной.
Существуют и другие приемы и методы повышения агрессивности портфелей
ценных бумаг. Общее направление этих приемов и методов состоит в повышении
доходности портфелей путем различного комбинирования их составов, в
своевременной реализации одних, менее перспективных, бумаг и приобретении
других – более перспективных. Для успешного осуществления задачи роста ценности
портфеля необходимо глубокое знание и понимание сущности функционирования
фондового рынка, а также постоянный его анализ и надежное прогнозирование.
Знание ожидаемой доходности активов, а также уровня
риска ее получения используются при формировании инвесторами так называемых
оптимальных портфелей ценных бумаг. Оптимизация портфеля ценных бумаг состоит
в определении пропорций в составе входящих в него активов, которые бы
обеспечили максимальную доходность при минимуме риска. При этом следует
отметить, что, как правило, чем выше предполагаемая доходность актива, тем выше
и степень риска ее получения. И наоборот, активы, по которым имеется высокая
гарантированность получения дохода, имеют гораздо меньшую доходность. К ним
относятся в частности государственные облигации.
Основную
проблему, которую необходимо решать при формировании портфеля ценных бумаг,
составляет задача распределения инвестором определенной суммы денег по
различным альтернативным вложениям (например, акции, облигации, наличные деньги
и др.) так, чтобы наилучшим образом достичь своих целей.
В первую очередь
инвестор стремится к получению максимального дохода за счет: выигрыша от
благоприятного курса акций; дивидендов; получения твердых процентов и т.д. С
другой стороны, любое вложение капитала связано не только с ожиданием получения
дохода, но и с постоянной опасностью проигрыша, а значит, в оптимизационных
задачах по выбору портфеля ценных бумаг необходимо учитывать риск. [7, с.106]
В принципе для создания портфеля ценных бумаг достаточно инвестировать
деньги в какой-либо один вид финансовых активов. Но современная экономическая
практика показывает, что такой однородный по содержанию портфель
(недиверсифицируемый) встречается очень редко. Гораздо более распространенной
формой является так называемый диверсифицированный портфель, т.е. портфель с
самыми разнообразными ценными бумагами. Использование диверсифицированного
портфеля элиминирует разброс в нормах доходности различных финансовых активов.
Нынешнее состояние финансового рынка заставляет быстро и адекватно
реагировать на его изменения, поэтому роль управления инвестиционным портфелем
резко возрастает и заключается в нахождении той грани между ликвидностью,
доходностью и рискованностью, которая позволила бы выбрать оптимальную
структуру портфеля. [2, ср.340]
Принцип нахождения оптимального портфеля ценных бумаг состоит в
рассмотрении вариаций его состава с различными пропорциями состава активов и в
расчете для каждого варианта среднего уровня доходности и показателя
ковариации. В соответствии с данными показателями инвестор или его доверенное
лицо, управляющее портфелем, принимают соответствующие решения по изменению состава
портфеля.
Задача формирования модели оптимального
портфеля ценных бумаг заключается в том, чтобы из трех активов составить
такой портфель, который обеспечивал бы инвестору минимальный риск при требуемой
доходности. Для этой цели необходимо определить количество каждого из активов
моделируемого портфеля ценных бумаг.
Довольно часто при составлении бюджета капитальных вложений приходится
учитывать ряд ограничений. Например, имеется несколько привлекательных
инвестиционных проектов, однако предприятие из-за ограниченности в финансовых ресурсах не может осуществить их
все одновременно. В этом случае необходимо отобрать для реализации проекты так,
чтобы получить максимальную выгоду от инвестирования. Как правило, основной целевой установкой в
подобных случаях является максимизация суммарного NPV. Рассмотрим наиболее
типовые ситуации, требующие оптимизации распределения инвестиций. Более сложные
задачи оптимизации инвестиционных портфелей решаются с помощью методов
линейного программирования.
Рекомендации по пространственной оптимизации
Пространственная оптимизация бюджета
капиталовложений проводится при наличии определенных условий[17, с. 177]:
·
общая сумма финансовых ресурсов на конкретный
период (например, год) ограничена сверху;
·
имеется несколько независимых проектов с
суммарным объемом требуемых инвестиций, превышающим имеющиеся у предприятия
ресурсы;
·
требуется составить инвестиционный портфель,
максимизирующий суммарный возможный прирост капитала.
На первый взгляд, в портфель нужно включить все проекты с максимальным
значением NPV. Такое решение является самым простым, но не обязательно
оптимальным. Кроме того, если число конкурирующих проектов велико, то перебор
вариантов на предмет соответствия ограничению по объему суммарных инвестиций
может быть достаточно утомительным.
В зависимости от того, поддаются дроблению рассматриваемые проекты или
нет, возможны различные способы решения данной задачи. Рассмотрим их
последовательно.
Рассматриваемые проекты поддаются дроблению
Допустим, что рассматриваемые проекты поддаются дроблению, т. е. можно
реализовать не только полностью каждый из анализируемых проектов, но и любую
его часть (при этом берется к рассмотрению соответствующая доля инвестиций и
денежных поступлений). Так как в этом случае объем инвестиций по любому проекту
может быть сколь угодно малым, максимальный суммарный эффект достигается при
наибольшей эффективности использования вложенных средств. Выше отмечалось, что
критерием, характеризующим эффективность использования каждого инвестированного
рубля, является показатель РI.
При прочих равных условиях проекты, имеющие наибольшие значения РI, являются более
предпочтительными с позиции отдачи на инвестированный капитал.
Порядок оптимизации следующий:
·
для каждого проекта рассчитывается PI;
·
проекты упорядочиваются по убыванию РI;
·
в инвестиционный портфель включаются первые k
проектов, которые в сумме в полном объеме могут быть профинансированы
предприятием;
·
очередной проект берется не в полном объеме, а
лишь в той части, в которой он может быть профинансирован.
Рассмотрим пример.
Пример
Предприятие имеет возможность инвестировать а) до 55 млн руб.; б) до 90
млн руб., при этом цена источников финансирования составляет 10%. Требуется
составить оптимальный инвестиционный портфель, если имеются следующие
альтернативные проекты
Таблица 13
Исходные данные по проектам в составе портфеля
|
Проект А
|
-30
|
6
|
11
|
13
|
12
|
|
Проект В
|
-20
|
4
|
8
|
12
|
5
|
|
Проект С
|
-40
|
12
|
15
|
15
|
15
|
|
Проект Д
|
-15
|
4
|
5
|
6
|
6
|
Рассчитаем чистый приведенный доход (NPV) и индекс рентабельности (РI) для каждого проекта:
проект А: NPV = 2,51; PI = 1,084; IRR = 13,4%
проект В: NPV = 2,68; PI = 1,134; IRR = 15,6%
проект С: NPV = 4,82; PI = 1,121; IRR = 15,3%
проект D: NPV = 1,37; PI = 1,091; IRR = 13,9%.
Таким образом, по убыванию показателя PI проекты упорядочиваются следующим образом: B, C, D, A.
Наиболее оптимальная структура бюджета капиталовложений для варианта (а)
представлена в таблице 14
Таблица 14
Оптимальная структура бюджета капиталовложений инвестора
|
Проект
|
Величина инвестиций
|
Часть инвестиций,
включаемая в портфель, %
|
NPV
|
|
В
|
20
|
100,0
|
2,68
|
|
С
|
35
|
87,5
|
4,22
|
|
Всего
|
55
|
|
6,90
|
Можно проверить, что любое другое сочетание ухудшает результаты -
уменьшает суммарный NPV. В частности, проверим вариант, когда проект С, как
имеющий наивысший NPV, в полном объеме включается в портфель (см. табл. 15).
Таблица 15
Портфель
|
Проект
|
Величина
инвестиций
|
Часть
инвестиций, включаемая в портфель, %
|
NPV
|
|
С
|
40
|
100,0
|
4,82
|
|
В
|
15
|
75,0
|
2,01
|
|
Всего
|
55
|
|
6,83
|
Таким образом, действительно была найдена
оптимальная стратегия формирования инвестиционного портфеля. Наиболее
оптимальная структура инвестиционного портфеля для варианта (б) представлена в
таблице 16
Таблица 16
Оптимальная
структура инвестиционного проекта
|
Проект
|
Величина
инвестиций
|
Часть
инвестиций, включаемая в портфель, %
|
NPV
|
|
В
|
20
|
100,0
|
2,68
|
|
С
|
40
|
100,0
|
4,82
|
|
D
|
15
|
100,0
|
1,37
|
|
A
|
15
|
50,0
|
1,26
|
|
Всего
|
90
|
|
10,13
|
Рассматриваемые проекты не поддаются дроблению
Если рассматриваемые проекты дроблению не поддаются, оптимальную
структуру бюджета капиталовложений определяют перебором всех возможных
вариантов сочетания проектов и расчетом суммарного NPV для каждого варианта.
Комбинация, максимизирующая суммарный NPV, будет оптимальной. Рассмотрим
пример.
Пример
В условиях предыдущего примера составить оптимальный инвестиционный
портфель, если верхний предел величины вложений составляет 55 млн руб. и
проекты не поддаются дроблению.
Возможны следующие сочетания проектов в портфеле: А+В, A+D, B+D, C+D.
Рассчитаем суммарный NPV для каждого варианта (см. табл. 17).
Таблица 17
Сочетания проектов в
портфеле
|
Вариант
|
Суммарные
инвестиции
|
Суммарный
NPV
|
|
А
+ В
|
50
(30 + 20)
|
5,19
(2,51 + 2,68)
|
|
А
+ D
|
45(30+15)
|
3,88
(2,51 + 1,37)
|
|
В
+ D
|
35(20+15)
|
4,05
(2,68 + 1,37)
|
|
С
+ D
|
55(40+15)
|
6,19
(4,82 + 1,37)
|
Итак, оптимальным является инвестиционный портфель, включающий проекты С и D.
Временная оптимизация
Временная оптимизация бюджета капиталовложений может
проводиться, если[14,с .177]:
·
общая сумма финансовых ресурсов, доступных в
планируемом году, ограничена сверху;
·
имеется несколько независимых инвестиционных
проектов, которые ввиду ограниченности финансовых ресурсов не могут быть
реализованы в планируемом году одновременно, однако в году, следующем за
планируемым, оставшиеся проекты либо их части могут быть реализованы;
·
требуется оптимальным образом распределить
проекты по двум годам.
В основу методики временной оптимизации инвестиционного портфеля положен
расчет специального индекса по каждому проекту, характеризующего относительную
потерю NPV в случае
отсрочки исполнения проекта на год. Проекты с минимальными значениями индекса
могут быть отложены на следующий год. Очевидно, что ключевую роль в данной
методике вновь играет показатель РI. Рассмотрим пример.
Пример
В условиях примера для проектов,
поддающихся дроблению, необходимо составить оптимальный инвестиционный портфель
на два года, если объем инвестиций на планируемый год ограничен суммой 70 млн руб.
Рассчитаем потери в NPV в случае, если каждый из анализируемых проектов
будет отсрочен к исполнению на год (см. табл. 18).
Таблица 18
Потери по проектам
|
Проект
|
NPV в году 1
|
Дисконти-рующий
множитель при r=10%
|
NPV в году 0
|
Потеря в NPV
|
Величина отложенных
на год инвестиций
|
Индекс возможных
потерь
|
|
А
|
2,51
|
0,9091
|
2,28
|
0,23=2,51-2,28
|
30
|
0,0077=0,23/30
|
|
В
|
2,68
|
0,9091
|
2,44
|
0,24
|
20
|
0,0120
|
|
С
|
4,82
|
0,9091
|
4,38
|
0,44
|
40
|
0,0110
|
|
D
|
1,37
|
0,9091
|
1,25
|
0,12
|
15
|
0,0080
|
Индекс возможных потерь показывает величину относительных потерь,
если исполнение проекта отложено на год.
Наименьшие потери при этом будут по проекту А, затем, соответственно, по
проектам D, C, B. Таким образом, портфель первого года должен включить проекты
В и С в полном объеме, а также часть проекта D; оставшуюся часть проекта D и
проект А следует включить в портфель второго года (см. табл. 19).
Таблица 19
Портфель второго ряда
|
Проект
|
Величина инвестиций
|
Часть инвестиций,
включаемая в портфель, %
|
NPV
|
|
а) инвестиции в
году 0
|
|
|
|
|
В
|
20
|
100
|
2,68
|
|
С
|
40
|
100
|
4,82
|
|
D
|
10
|
67=10/15
|
0,92=1,37×0,67
|
|
Всего
|
70
|
|
8,42
|
|
б) инвестиции в
году 1
|
|
|
|
|
D
|
5
|
33
|
0,41=1,25×
0,33
|
|
A
|
30
|
100
|
2,28=2,51×0,9091
|
|
Всего
|
35
|
|
2,69
|
Суммарный NPV при таком формировании портфелей за два года составит 11,11
млн руб. (8,42 + 2,69), а общие потери составят 0,27 млн руб. (2,51 + 2,68 +
4,82 +1,37 -11,11) и будут минимальны по сравнению с другими вариантами
формирования портфелей.
Оптимизация в условиях
реинвестирования доходов
Рассмотренными в предыдущих разделах примерами, естественно, не
исчерпывается множество ситуаций, когда приходится принимать во внимание
различные ограничения; кроме того, понятно, что далеко не каждая ситуация,
встречающаяся на практике, может быть описана достаточно строгими
аналитическими зависимостями. Также очевидным является факт, что любая подобная
формализация всегда сопровождается некоторыми условностями и дополнительными
ограничениями, осложняющими использование рассмотренных критериев. Приведем еще
один пример, показывающий, что традиционные рекомендации, в частности, в
отношении критерия РI
не всегда оправданны.
Пример
Предприятие имеет возможность инвестировать ежегодно не более 20 млн руб.
Кроме того, все доходы от дополнительно реализованных инвестиционных проектов
могут использоваться для целей инвестирования. На момент анализа являются
доступными следующие независимые проекты (см. табл. 20).
Таблица 20
Исходные данные
|
Проект
|
Год
0
|
Год
1
|
Год
2
|
|
А
|
-20
|
25
|
7
|
|
В
|
-15
|
4
|
30
|
|
С
|
-5
|
8
|
8
|
|
D
|
-
|
-45
|
69
|
Необходимо составить
инвестиционный портфель, если цена источников финансирования равна 12%. Прежде
чем приступить к формированию портфеля, следует рассчитать значения критериев
NPV и РI для каждого
проекта при цене капитала, СС = 12% (см. табл. 21).
Таблица 21
Инвестиционный портфель
|
NPV
|
РI
|
|
А
|
7,9
|
1,40
|
|
В
|
12,5
|
1,83
|
|
С
|
8,5
|
2,70
|
|
D
|
15,6
|
1,37
|
Следует отметить, что критерий PI в данном случае рассчитывается как
отношение приведенных стоимостей денежных притоков (IF) и денежных оттоков (OF), причем расчет ведется на
конец года 0. В частности, для проекта D:
PV IF = 69/(1+0,12)2=55,0
млн руб., PV OF = 45/(1+0,12) = 40,1 млн руб. Таким образом, РI
проекта D составляет 1,37.
По критерию NPV все проекты являются приемлемыми. Критерий РI дает возможность ранжировать
их по степени предпочтительности: С, В, А, D. Что касается составления портфеля
капиталовложений, то число вариантов здесь ограничено.
Поскольку объем капиталовложений нулевого года ограничен 20 млн руб.,
предприятие может принять либо проект А, либо комбинацию проектов В и С. С
позиции критерия РI
комбинация проектов В и С более выгодна,
суммарный NPV в этом случае равен 21 млн руб. С другой стороны, принятие
этой комбинации делает невозможным реализацию проекта D: предприятие не будет
иметь источников средств в достаточном объеме, так как сумма, на которую может
рассчитывать предприятие, равна 32 млн руб. (20 млн руб. из запланированных
источников и 12 млн руб., генерируемых проектами В и С). Если же будет принят
проект А, то к концу первого года у предприятия появятся средства и для
принятия проекта D: 20 млн руб. из запланированных источников плюс 25 млн руб.,
генерируемых проектом А. Речь идет о выборе между комбинацией (В+С), с одной
стороны, и комбинацией (А+D) - с другой. Поскольку вторая комбинация
обеспечивает большее значение совокупного NPV (7,9 + 14,8 = 22,7 млн руб.), то она является более
предпочтительной. Таким образом, критерий РI в рассматриваемом случае не срабатывает, и приходится прибегать
к критерию NPV.
ЗАКЛЮЧЕНИЕ
Под инвестированием понимают вложение в реализацию различных
экономических проектов денежных средств и других капиталов с целью последующего
их увеличения, а сами вкладываемые средства называются инвестициями. В практике
производственной и финансово-хозяйственной деятельности принято различать
следующие типы инвестиций: реальные (капиталообразующие) инвестиции; портфельные
инвестиции; инвестиции в нематериальные активы. Инвестиционный проект
представляет собой совокупность соединенных воедино намерений и практических
действий по осуществлению инвестиционных вложений и обеспечению заданных
конкретных финансово-экономических, производственных и социальных результатов.
Управление инвестиционной деятельностью как в масштабах государства и его
территорий, так и в рамках отдельных хозяйствующих субъектов, в целях наиболее
эффективного использования имеющихся и привлекаемых инвестиционных ресурсов –
есть инвестиционный менеджмент. При этом инвестиционный менеджмент необходимо
рассматривать и как непосредственно процесс управления инвестиционной
деятельностью, и как научный метод, обеспечивающий эффективность этого
процесса.
Под ценными бумагами понимают документ, определяющий взаимоотношения
между лицом, выпустившим такой документ, и его владельцем и закрепляющий за
владельцем определенный набор имущественных прав, реализация которых возможна
лишь при предъявлении самого документа. Вложения в ценные бумаги требуют
эффективного управления. В этой связи существует понятие управления портфелем
ценных бумаг, который представляет собой некую совокупность ценных бумаг,
выступающую как целостный объект управления. Наиболее важными параметрами в
управлении портфелем ценных бумаг являются: доходность портфеля и его риск.
Доходность портфеля зависит от ожидаемых доходностей входящих в него различных
активов. Риск портфеля ценных бумаг зависит от сочетания стандартных отклонений
(дисперсий) активов и степени взаимосвязи и направления изменения доходностей
(ковариаций) активов, входящих в его состав.
Знание ожидаемой доходности активов, а также уровня риска ее получения
используются при формировании инвесторами так называемых оптимальных портфелей
ценных бумаг. Оптимизация портфеля ценных бумаг состоит в определении
пропорций в составе входящих в него активов, которые бы обеспечили максимальную
доходность при минимуме риска.
В данной работе представлена статическая модель оптимального портфеля
ценных бумаг. Эта модель может быть использована при инвестировании, управлении
портфелем ценных бумаг отдельным предпринимателем или инвестором для более
успешной предпринимательской деятельности. Недостатком данной модели является
то, что она не учитывает влияние всех факторов, влияющих на риск портфеля
ценных бумаг. Также к недостатку данной модели можно отнести и тот факт, что не
для всех ценных бумаг можно составить статистический ряд доходности актива за
предыдущие периоды.
Существуют различные модели оптимизации портфеля ценных бумаг (такие как
модель Марковица, индексная модель Шарпа, модель выровненной цены и др.). Все
они так или иначе имеют некоторые недостатки, но применение их на практике дает
значительные преимущества при управлении портфелем ценных бумаг.
В целом любые модели инвестиционного портфеля
являются открытыми системами и соответственно могут дополняться и корректироваться
при изменениях условий на финансовом рынке. Модель инвестиционного портфеля
позволяет получить аналитический материал, необходимый для принятия
оптимального решения в процессе инвестиционной деятельности.
Получение
математической оценки состояния портфеля на разных этапах инвестирования при
учете влияния различных факторов делает возможным непрерывно управлять
структурой портфеля на каждом этапе принятия решения, т.е. по сути дела
управлять рисками.
Использование
компьютерной реализации моделей значительно увеличивает оперативность получения
аналитического материала для принятия решений. Следовательно, выполняются такие
основные свойства управления как: эффективность, непрерывность и оперативность.
СПИСОК ЛИТЕРАТУРЫ
1. Агасандян Г.А. Элементы
многопериодной портфельной модели. — М.: Вычислительный центр РАН, 2002. – 453
с.
2. Балабанов И.Т. Основы финансового
менеджмента. – М. : Финансы и
статистика, 2001. – 245 с.
3. Бессонов
Д.Н., Недосекин А.О. Корреляционная матрица и ее роль в оптимизации фондового
портфеля. - М. : Финансы и статистика, 2003. – 156 с.
4. Бланк
И.А. Словарь‑справочник финансового менеджера. – К.: «Ника‑Центр»,
2003. – 670 с.
5. Бочаров
В.В. Инвестиционный менеджмент (управление инвестициями): Учебное пособие. – С‑Пб.:
Издательство С‑ПбУЭФ, 2003. – 156 с.
6. Галанов В.А., Басов А.И.
Рынок ценных бумаг. - М. : Финансы и статистика, 2001. – 267 с.
7. Ильина
Л.И. Организация и финансирование инвестиций: Учебное пособие. – Сыктывкар,
2002 – 289 с.
8. Колесников В.И.,
Торкановский В.С. Ценные бумаги. - М.%
Финансы и статистика, 2001. – 560 с.
9. Кузьмина Л. Анализ
производственных инвестиций \\ Финансовая
газета. – 2001. - №10,11. – С. 26 - 39
10.
Любушин Н.П. Анализ финансово-экономической деятельности
предприятия. - М. : Юнити-Дана, 2000 . – 356 с.
11.
Мартынов А. Возможности повышения эффективности инвестиций
\\ Экономист. – 2000. - № 9. – С. 78
12.
Минаев Ю.Н. Стабильность экономико-математических моделей
оптимизации. — М.: Статистика, 2000. – 256 с.
13.
Мищенко А.В., Попов А.А. Двухкритериальная задача оптимизации
инвестиционного портфеля в условиях ограничений на финансовые
ресурсы//Менеджмент в России и за рубежом. — 2001. — № 3. – С. 25
14.
Мищенко А.В., Попов А.А. Модели управления портфелем ценных
бумаг//Рос. экон. акад. — 1999. - № 1. – С. 18
15.
Мищенко А.В. Модели распределения ограниченных ресурсов//Рос.
экон. акад. — 1992. - № 12. – С. 23
16.
Мищенко А.В., Попов А.А. Двухкритериальная задача оптимизации
инвестиционного портфеля в условиях ограничений на финансовые ресурсы \\
Менеджмент в России и за рубежом. – 2001. - № 1. – С. 15 - 27
17.
Недосекин А.О. Нечетко-множественный анализ
рисков фондовых инвестиций. - СПб.:
Типография «Сезам», 2002. – 278 с.
18.
Недосекин А.О. Фондовый менеджмент в
расплывчатых условиях. - СПб,
Типография «Сезам», 2003. – 450 с.
19.
Недосекин А.О. Персональная страница в
Интернете. – На сайте: http://sedok.narod.ru/sc_group.html
20.
Недосекин А.О.Прогнозирование фондовых индексов
// Аудит и финансовый анализ. – 2002. – 2002. – С. 14 - 19
21.
Нечаев Н. Инвестиционный портфель: формирование и управление
\\ Экономика и Жизнь. – 2001. - № 14 . – С. 67
22.
Овчинников В. Путь к совершенствованию глобального рынка
портфельных и прямых инвестиций \\ Маркетинг. – 2002. - № 2. – С. 16
23.
Райзберг Б.А., Лозовский Л.Ш., Стародубцева Е.Б. Современный
энциклопедический словарь. – М. : ИНФРА-М, 2003. – 459 с.
24.
Ромакин М.И. Математический аппарат оптимизационных задач. —
М.: Статистика, 2001. – 290 с.
25.
Рынок ценных бумаг/Под ред. акад. А.И.Басова, В.А. Галанова.
— М.: Финансы и статистика, 2001. – 230 с.
26.
Серов В.М. Инвестиционный менеджмент. - М. :
ИНФРА-М, 2000. – 256 с.
27.
Слуцкин Л.Н. Активный и пассивный портфельный
менеджмент // Банковские технологии. – 2001. – № 7. – С. 15
28.
Тренев Н.Н. Управление финансами. Учебное пособие. — М.:
Финансы и статистика, 2000. – 378 с.
29.
Ху Т. Целочисленное программирование и потоки в сетях. — М.:
Мир, 2001. – 287 с.
30.
Шарп У., Александер Г., Бэйли Дж. Инвестиции:
Пер. с англ. – М.: Инфра‑М, 2001. – 189 с.
31.
Щербак В.Е. Институциональный анализ инвестиционного планирования
и проектирования \\ ЭКО. – 2002. - № 3.
– С. 76
ПРИЛОЖЕНИЯ
Приложение 1
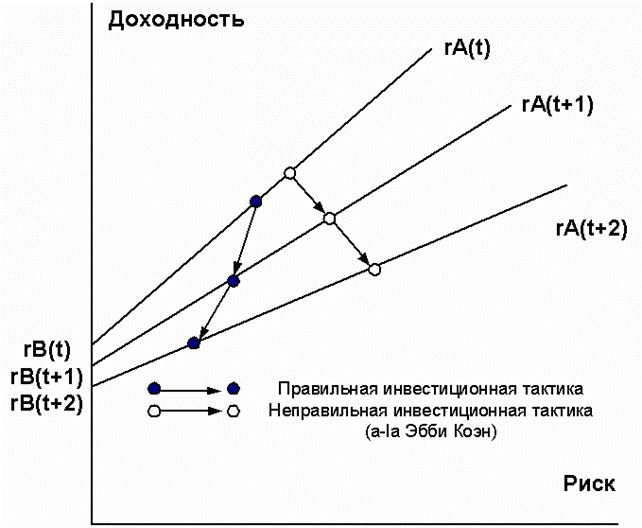
Рис. 1. Инвестиционная
тактика «Доходность – риск»
Приложение 2
Таблица
2
|
Период
|
доходность %
|
|
актив А
|
актив Б
|
актив С
|
|
1
|
23
|
25
|
24
|
|
2
|
27
|
26
|
26
|
|
3
|
33
|
25
|
29
|
|
4
|
32
|
27
|
33
|
|
5
|
28
|
28
|
28
|
|
6
|
29
|
26
|
31
|
|
7
|
34
|
24
|
35
|
|
8
|
36
|
24
|
38
|
|
9
|
33
|
23
|
36
|
|
10
|
31
|
25
|
41
|
|
11
|
25
|
26
|
39
|
|
12
|
27
|
25
|
33
|
|
13
|
28
|
27
|
28
|
|
14
|
30
|
26
|
32
|
|
15
|
32
|
24
|
36
|
|
16
|
35
|
23
|
39
|
|
17
|
37
|
23
|
35
|
|
18
|
36
|
25
|
40
|
|
19
|
35
|
24
|
42
|
|
20
|
32
|
25
|
36
|
|
21
|
30
|
26
|
31
|
|
22
|
33
|
26
|
32
|
Приложение 3
Таблица 10
Нечеткий классификатор факторов
|
Уровень
показателя
|
Диапазон
значений для факторов:
|
|
P/E
для Cap
|
Cap,
|
ROE %
|
D/Eq
|
P/B
|
|
< 1 млрд
|
>
1 млрд
|
млн.
$
|
|
Очень
низкий(ОН)
|
30
- ∞
|
45
- ∞
|
0-50
|
<
0
|
>
1
|
>
4.5
|
|
ОН-Н
|
25-30
|
40-45
|
50-100
|
0
– 5%
|
0.7
– 1
|
4
- 4.5
|
|
Низкий
(Н)
|
20-25
|
30-40
|
100-300
|
5
- 10%
|
0.4
– 0.7
|
3.5
- 4
|
|
Н-Ср
|
15-20
|
25-30
|
300-500
|
10-15%
|
0.3
– 0.4
|
3
- 3.5
|
|
Средний
(Ср)
|
10-15
|
20-25
|
500-1000
|
15
- 25%
|
0.2
– 0.3
|
2.5
- 3
|
|
Ср-В
|
7-10
|
15-20
|
1000-3000
|
25-30%
|
0.15
– 0.2
|
2
- 2.5
|
|
Высокий
(В)
|
5-7
|
10-15
|
3000-5000
|
30-35%
|
0.1
– 0.15
|
1.5
- 2
|
|
В
– ОВ
|
5-5
|
10-10
|
5000-10000
|
35-40%
|
0.05
- 0.1
|
1
- 1.5
|
|
Очень
высокий (ОВ)
|
2-5
|
5-10
|
Свыше
10000
|
>40%
|
0
– 0.05
|
<1
|
Приложение 4
Таблица 11
Функция принадлежности для интегрального показателя «Оценка
бумаги»
|
Значение A_N
|
Значения функций
принадлежности для подмножеств
переменной «Оценка
бумаги»:
|
|
ОН
|
Н
|
Ср
|
В
|
ОВ
|
|
0-0.15
|
1
|
0
|
0
|
0
|
0
|
|
0.15-0.25
|
(0.25-A_N)*10
|
(A_N-0.15)*10
|
0
|
0
|
0
|
|
0.25-0.35
|
0
|
1
|
0
|
0
|
0
|
|
0.35-0.45
|
0
|
(0.45-A_N)*10
|
(A_N-0.35)*10
|
0
|
0
|
|
0.45-0.55
|
0
|
0
|
1
|
0
|
0
|
|
0.55-0.65
|
0
|
0
|
(0.65-A_N)*10
|
(A_N-0.55)*10
|
0
|
|
0.65-0.75
|
0
|
0
|
0
|
1
|
0
|
|
0.75-0.85
|
0
|
0
|
0
|
(0.85-A_N)*10
|
(A_N-0.75)*10
|
|
0.85-1.0
|
0
|
0
|
0
|
0
|
1
|