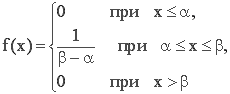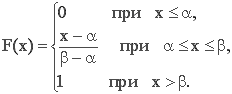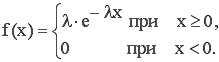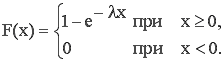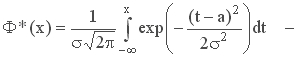Вариант 6
Содержание
1. Приведите примеры номинальных шкал. 2
2. Привести примеры распределения непрерывных случайных величин 4
Решение задач. 9
Список литературы.. 15
1. Приведите примеры номинальных шкал
Номинальная шкала – метрическая шкала, отображающая лишь отношение эквивалентности между элементами измеряемой области. При этом данные элементы группируются в отдельные непересекающиеся классы, получающие номера или названия, и номер класса фактически не имеет количественного выражения.
Номинальная шкала - основа всех шкальных процедур. Она устанавливает отношения равенства между явлениями, которые включены в один класс.
Пример номинальной шкалы:
1. Рабочие ручного труда, не требующего специальной подготовки.
2. Рабочие ручного труда высокой квалификации.
3. Рабочие механизированного труда средней квалификации
4. Рабочие механизированного труда высокой квалификации.
5. Рабочие автоматизированного труда.
6. Рабочие, занятые наладкой автоматизированного оборудования.
В этой шкале каждому из пунктов дается детальная эмпирическая интерпретация. Рабочие перечислены по мере роста их квалификации.
Операции с числами для номинальной шкалы следующие:
o Нахождение частот распределения по пунктам шкалы в единицах или процентах от общего количества.
o Поиск средней тенденции по модальной частоте. Модальной называют группу с наибольшей численностью в данном измерении. Упорядоченная номинальная шкала чаще всего используется при опросах общественного мнения. Пример такой шкалы:
§ "вполне согласен",
§ "пожалуй, согласен",
§ "затрудняюсь ответить",
§ "пожалуй, не согласен",
§ "не согласен",
§ "совершенно не согласен".
Весьма часто употребляемые разновидности шкал этого типа - ранговые. Они предполагают полное упорядочение каких-либо объектов или свойств от наиболее к наименее важному, значимому, предпочитаемому. Можно ранжировать относительную важность тех или иных методов решения крупных экономических, политических или социальных проблем, предпочтительное использование свободного времени. Задание на ранжирование формулируется примерно так: "Из перечисленных ниже суждений выберите самое для вас предпочтительное, затем - наименее предпочтительное, а остальные расположите от первого до последнего". То есть респондент указывает ранги предложенных вариантов. Полезно не забывать, что численность объектов для ранжирования не должна быть большой - до 10. В противном случае результаты ранжирования будут неустойчивыми.
Применение количественных методов и использование статистики социальных явлений возводит социологию в ранг строгой науки. Создается впечатление математической точности выводов. Между тем квантификация сложных социальных реалий накладывает немало ограничений на собственно математические операции с их измерениями. Математик работает с простыми однозначными абстракциями, в основе которых суждение "есть - нет". Социолог обязан помнить, что в действительности скрывается за величинами, которыми он оперирует. Главное состоит в том, что количественный анализ не самоцель, а лишь средство качественного анализа.
В теории измерений номинальные шкалы считаются простейшими и самыми «бедными» (их называют также шкалами наименований и классификационными шкалами). Если обозначить числами возможные варианты ответов испытуемого на тестовые задания, то эти числа будут иметь смысл только абстрактных символов, обозначающих каждый вариант ответов и никакие другие отношения между указанными числами, кроме их равенства, значения не имеют. При сравнении двух испытуемых по признаку, измеренному в номинальной шкале, можно сделать единственный вывод о совпадении или несовпадении значения признака. Поэтому при анализе таких признаков каждую отметку номинальной шкалы считают отдельным самостоятельным признаком. Он принимает всего два значения А и В и разность (А — В) уже может интерпретироваться как степень важности несовпадения данного признака при сравнении двух объектов. Чаще всего применяют значения А=0 и В=1, то есть признак равен либо 0, либо 1, а степень важности признака xi задается весом wi, на который умножается xi. Такие признаки называют двоичными, бинарными, булевыми, а в психодиагностике часто используют термин «дихотомические признаки». Процедура преобразования исходных показателей в набор признаков с двумя градациями носит название дихотомизации. После проведения дихотомизации номинальные измерения становятся доступны для применения широкого спектра различных методов многомерного количественного анализа с учетом специфики данного вида измерений.
2. Привести примеры распределения непрерывных случайных величин
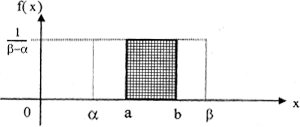
Равномерный закон распределения. СВ X распределена по равномерному (прямоугольному) закону, если все значения СВ лежат внутри некоторого интервала и все они равновероятны (точнее обладают одной плотностью вероятности). Например, если весы имеют точность 1г и полученное значение округляется до ближайшего целого числа k, то точный вес можно считать равномерно распределенной СВ на интервале (k-0,5; k+0,5).
Дифференциальная функция равномерного закона на интервале (a,b) (рис. 1):
|
|
|
Интегральная функция равномерного закона на интервале (a,b) (рис. 1):
|
|
|
|
|
|
|
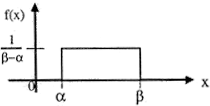
Дифференциальная функция |
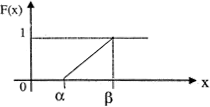
Интегральная функция |
|
Рис. 1. Равномерный закон распределения |
Основные числовые характеристики равномерного закона:
1. Математическое ожидание:
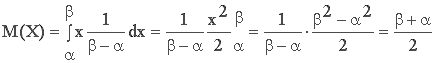
М(Х) совпадает, в силу симметрии распределения, с медианой.
2. Моды равномерное распределение не имеет.
3. Дисперсия:
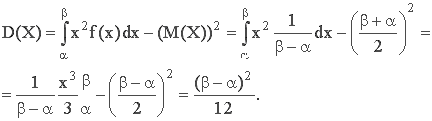
Отсюда, среднее квадратическое отклонение:
![]()
4. Третий центральный момент:
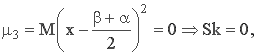
поэтому распределение симметрично относительно М(Х).
5. Четвертый центральный момент:
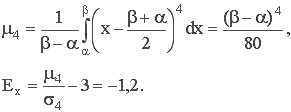
6. Вероятность попадания СВ в заданный интервал (а;b).
Пусть СВ X распределена по равномерному закону, тогда (рис.2):
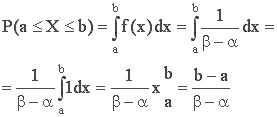
|
|
|
Рис. 2. Вероятность попадания равномерно распределенной СВ Х в (а;b) |
Показательное распределение. НСВ X, принимающая неотрицательные значения, имеет показательное распределение, если ее дифференциальная функция имеет вид:
|
|
|
где l = const, l > 0.
Интегральная функция показательного закона с параметром l:
|
|
|
|
|
|
|
Дифференциальная функция |
Интегральная функция |
|
Рис. 3. Показательный закон |
Если СВ X распределена по показательному закону, то:
1.
Математическое
ожидание ![]()
2.
Дисперсия
![]()
среднее квадратическое отклонение ![]()
3. Вероятность попадания СВ X в заданный интервал определяется по формуле:
![]() .
.
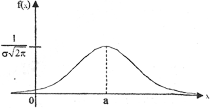
Нормальный закон распределения (рис. 10) играет исключительную роль в теории вероятностей. Это наиболее часто встречающийся закон распределения, главной особенностью которого является то, что он является предельным законом, к которому, при определённых условиях, приближаются другие законы распределения.
Дифференциальная функция нормального закона имеет вид (рис. 4):
|
|
|
Числовые характеристики нормального закона:
1. Математическое ожидание характеризует центр распределения:
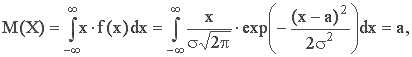
где ex=exp(x);
2. Дисперсия характеризует форму распределения:
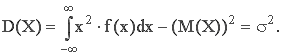
Свойства дифференциальной функции нормального закона:
1. Область определения: Dr = R;
2. Ось ОХ - горизонтальная асимптота;
3. х = а ± s - две точки перегиба;
4.
Максимум в точке
с координатами: 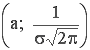 ;
;
5. График симметричен относительно прямой х=а;
6. Моменты:
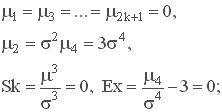
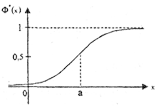
7. Вероятность попадания нормально распределенной случайной величины в заданный интервал определяется, по свойству интегральной функции:
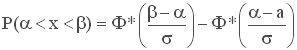 ,
,
где
|
|
|
интегральная функция нормального закона (рис. 4); Ф(х) - функция Лапласа.
|
|
|
|
Дифференциальная функция |
Интегральная функция |
|
Рис. 4. Нормальный закон распределения |
Свойства интегральной функции нормального закона:
1. Ф* (-¥)=0;
2. Ф*(+)=1;
3. Ф*(х)=1/2+Ф(х);
4. Ф*(-х)=1-Ф*(х).
Вероятность заданного отклонения. Правило трех сигм. Найдем вероятность того, что случайная величина X, распределённая по нормальному закону, отклонится от математического ожидания М(Х)=а не более чем на величину e>0.
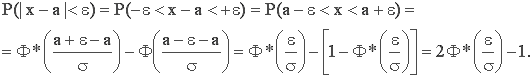
Или, используя функцию Лапласа:
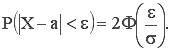
Найдём вероятность того, что нормально распределённая случайная величина X отклонится от М(Х)=а на s, 2s, Зs:
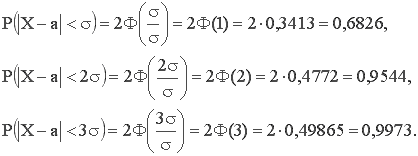
Отсюда следует правило Зs: если случайная величина X имеет нормальное распределение, то отклонение этой случайной величины от ее математического ожидания по абсолютной величине не превышает утроенное среднее квадратическое отклонение (Зs).
Решение задач
3. По таблице данных
а) проранжировать данные по возрастанию;
б) распределить по частотам;
в) сгруппировать по частотам;
г) интерпретировать полученные результаты целиком или в выбранной группе;
д) определить 25 процентиль данного распределения;
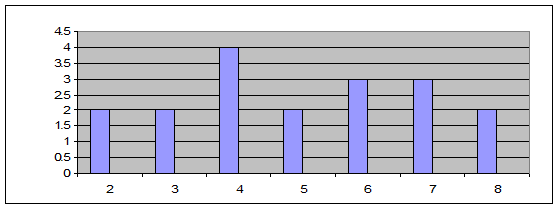
е) построить гистограмму распределения.
Таблица данных
|
№ |
Значение |
№ |
Значение |
№ |
Значение |
№ |
Значение |
|
1 |
1 |
6 |
6 |
11 |
3 |
16 |
6 |
|
2 |
5 |
7 |
5 |
12 |
7 |
17 |
8 |
|
3 |
4 |
8 |
2 |
13 |
8 |
18 |
4 |
|
4 |
6 |
9 |
3 |
14 |
2 |
19 |
7 |
|
5 |
4 |
10 |
4 |
15 |
7 |
20 |
6 |
а) 8 8 7 7 7 6 6 6 5 5 4 4 4 4 3 3 2 2
б) Число 8 встречается 2 раза, число 7 – 3 раза, число 6 – 3 раза, число 5 – 2 раза, число 4 – 4 раза, число 3 – 2 раза, число 2 – 2 раза.
в) группировка по частотам
|
Х – значение |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
n – частота |
2 |
2 |
4 |
2 |
3 |
3 |
2 |
г) Наибольшую частоту имеет значение 4. Большие значения частот встречаются в середине выборки. Крайние значения имеют меньшие частоты.
д) 25-я процентиль переменной - это
такое значение (xp), что 25% (p) значений переменной
попадают ниже этого значения. 25 процентиль данного распределения ![]()
е) Полигон распределения:
4. Число вариант в выборке нечетно,
значит медиана данного распределения ![]() .
.
Мода-наблюдение выборки, имеющее
наибольшую частоту. Для данного распределения мода ![]() .
.
![]()
Итак, медиана данного распределения равна 5, наибольшую частоту имеет значение 4, среднее значение данного распределения 5,06, т.е. среднее значение почти совпадает с модой.
5. Коэффициенты Пирсона
|
Х |
37 |
47 |
40 |
60 |
61 |
|
У |
60 |
86 |
67 |
92 |
95 |
|
N |
xi |
yi |
xi - |
(xi - |
yi - |
(yi - |
(xi- |
|
1 |
37 |
60 |
-12 |
144 |
-20 |
400 |
|
|
2 |
47 |
86 |
-2 |
4 |
6 |
36 |
-12 |
|
3 |
40 |
67 |
-9 |
81 |
-13 |
169 |
117 |
|
4 |
60 |
92 |
11 |
121 |
12 |
144 |
132 |
|
5 |
61 |
95 |
12 |
144 |
15 |
225 |
180 |
|
|
245 |
400 |
0 |
494 |
0 |
974 |
657 |
Вычислим
средние ![]() и
и ![]()
Вычислим выборочный коэффициент корреляции по формуле
![]()
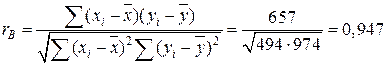
Уравнение регрессии У на Х :
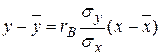 , где
, где 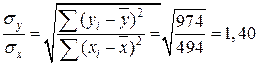
y-80=0,947×1,40(x-49)
y= 1,33x+145,16
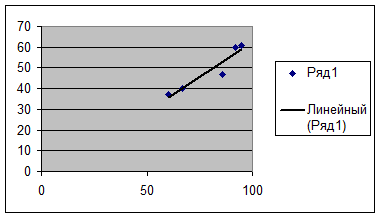
Представим графически уравнение регрессии Y на X и линию тренда
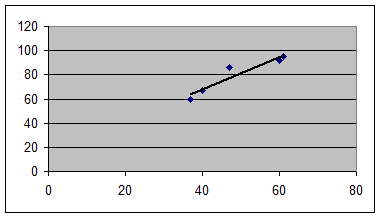
Уравнение регрессии Х на У :
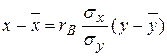 , где
, где 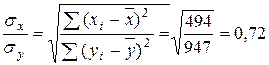
х-49=0,947·0,72(у-80)
х= 0,68у+103,72.
Представим графически уравнение регрессии X на Y и линию тренда
6. Х- скорость на первом участке дороги.
У- скорость на втором участке дороги.
|
№ |
Х |
У |
№ |
Х |
У |
|
1 |
62 |
85 |
6 |
62 |
95 |
|
2 |
65 |
89 |
7 |
75 |
83 |
|
3 |
61 |
83 |
8 |
70 |
87 |
|
4 |
71 |
92 |
9 |
62 |
83 |
|
5 |
63 |
85 |
10 |
71 |
90 |
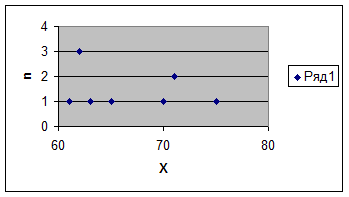
Составим закон распределения.
|
Х |
61 |
62 |
63 |
65 |
70 |
71 |
75 |
|
n |
1 |
3 |
1 |
1 |
1 |
2 |
1 |
Число вариант равно 7, m=4, ![]()
Мода-наблюдение выборки, имеющее
наибольшую частоту. ![]() .
.
![]()
|
У |
83 |
85 |
87 |
89 |
90 |
92 |
95 |
|
n |
3 |
2 |
1 |
1 |
1 |
1 |
1 |
Число вариант равно 7, m=4, ![]()
Мода-наблюдение выборки, имеющее
наибольшую частоту. ![]() .
.
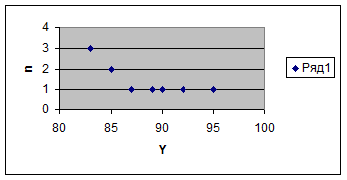 |
Средняя скорость на первом участке гораздо ниже чем на втором. Мода и медиана на первом участке различаются незначительно, на втором участке различия более значительные.
Список литературы
1. Глинский В.В., Ионин В.Г. Статистический анализ. Учебное пособие. – М.: Филинъ, 1998.
2. Долженкова В.Г. Статистика цен. – Новосибирск: НГАЭиУ, 1996.
3. Дубров А.М., Мхитарян В.С, Трошин Л.И. Многомерные статистические методы. – М.: Финансы и статистика, 1998.
4. Иванов А.Б. Методика анализа результатов обследования товарных рынков // Вопросы статистики, 1999, №3.
5. Статистика рынка товаров и услуг // Под ред. И.К. Беляковского. – М.: «Финансы и статистика», 1995.