5050701(8)

22.05

можно рукописно

345 руб. автору

Численные методы

Контрольная работа

Приближенные числа и действия над ними

Задание 1


  1. Определить какое равенство точнее.
  2. Округлить сомнительные цифры числа, оставив верные знаки: а) в узком смысле; б) в широком смысле. Определить абсолютную погрешность результата.
  3. Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры: а) в узком смысле; б) в широком смысле.


1) ;

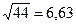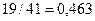
2) а) 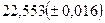 ; б) 2,8546; δ = 0,3 %

3) а) 0,2387; б) 42,884


Задание 2


Вычислить и определить погрешности результата


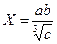, где , ,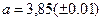


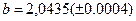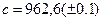
Приближенные решения алгебраических и трансцендентных уравнений


Отделить корни уравнения аналитически или графически и уточнить один из них с точностью до 0,001:

а)      Методом половинного деления

б)      Методом хорд и методом касательных

в)      Комбинированным методом

г)      Методом итераций


а)      а)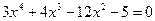

б)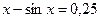     

в)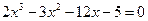     

г)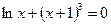     


Решение систем линейных алгебраических уравнений


Решить систему линейных алгебраических уравнений методом простой итерации и методом Зейделя


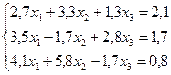
Интерполирование и экстраполирование функции

Задание 1


Найти приближенное значение функции при данном значении аргумента с помощью интерполяционного многочлена Лагранжа


x

y

1,375

5,04192

1,380

5,17744

1,385

5,32016

1,390

5,47069

1,395

5,62968

1,400

5,79788

x = 1,3832


Задание 2


Используя первую или вторую интерполяционные формулы Ньютона, вычислить значения функции при данных значениях аргумента. При составлении таблицы разностей контролировать вычисления.


X

y

1,415

0,888551

1,420

0,889599

1,425

0,890637

1,430

0,891667

1,435

0,892687

1,440

0,893698

1,445

0,894700

1,450

0,895693

1,455

0,896677

1,460

0,897653

1,465

0,898619

Значение аргумента

Х1

Х2

Х3

Х4

1,4161

1,4625

1,4135

1,470

Численное интегрирование


  1. Вычислить интеграл по формуле трапеций с тремя десятичными знаками
  2. Вычислить интеграл по формуле Симпсона при n=8; оценить погрешность результата, составив таблицу конечных разностей
  3. Вычислить интеграл по формуле Гаусса



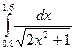
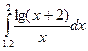
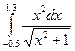
Численное решение обыкновенных дифференциальных уравнений


Используя метод Эйлера с уточнением, составить таблицу приближенных значений интеграла дифференциального уравнения y’=f(x,y), удовлетворяющего начальным условиям 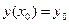 на отрезке [a,b]; шаг h=0,1. Все вычисления вести с четырьмя десятичными знаками.


 ; ,
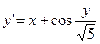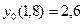