Вариант 4.
Задача 1. Анализ 10%
банковских счетов населения региона, выделенных в результате бесповторного
собственно-случайного отбора, показал следующее распределение:
|
Размер вклада, тыс. руб.
|
До 1,0
|
1,0-5,0
|
5,0-10,0
|
10,0-15,0
|
15,0 и более
|
|
Количество вкладов, %
|
20,0
|
25,0
|
40,0
|
10,0
|
5,0
|
Определите:
1. средний размер вклада;
2. с вероятностью р =
0,954 установите возможные пределы для всей совокупности вкладов населения:
а) среднего размера
вклада;
б) доли вкладов до 5 тыс.
руб.;
в) общей суммы вкладов.
Сделайте выводы.
Решение.
Для расчётов составим
вспомогательный вариационный ряд
|
хi
|
0,5
|
3
|
7,5
|
12,5
|
17,5
|
|
ni ,%
|
20
|
25
|
40
|
10
|
5
|
1. 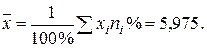
Для следующего действия
понадобится
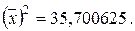
2. Сначала вычислим
дисперсию
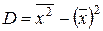
и среднее квадратическое
отклонение 
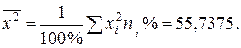
D = 20; 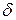 = 4,4762568.
= 4,4762568.
Ещё понадобится значение t = 2 из теории нормального закона распределения,
соответствующее доверительной вероятности Р = 0,954.
Размах доверительного
интервала для генеральной средней 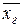 составляет
составляет
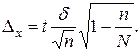
Из условия следует, что 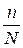 = 0,1, где
= 0,1, где
N – число
вкладчиков в регионе.
Значит, n
= 0,1 – объём выборки.
Получаем 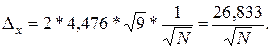
а) средний размер вклада 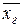 в регионе находится в
пределах
в регионе находится в
пределах
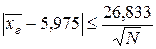 .
.
Если, например, N = 10 000, то 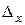 = 0,268 и средний вклад будет в пределах 5,707 ≤
= 0,268 и средний вклад будет в пределах 5,707 ≤ 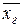 ≤ 6,243.
≤ 6,243.
б) доля вкладов до 5 тыс.
руб. по данным выборки составляет
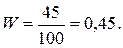
Для неё 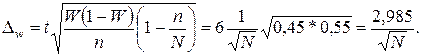
Для генеральной
совокупности
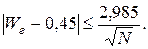
В частности, при N = 10 000 получаем 0,42 ≤ Wг ≤ 0,48.
в) 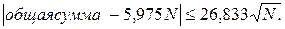
Задача 2. Имеются данные
о потерях рабочего времени на предприятии вследствие заболеваемости с временной
утратой трудоспособности
|
Год
|
1
|
2
|
3
|
4
|
5
|
6
|
|
Потери рабочего времени, чел.-дни
|
933,4
|
904,0
|
965,0
|
1014,1
|
1064,8
|
1122,9
|
1. Для определения
тенденции изменения потерь рабочего времени проведите аналитическое
выравнивание (подберите вид аналитической функции).
2. Отобразите фактические
и теоретические (выравненные) уровни ряда на графике. Покажите ожидаемые уровни
ряда на следующие 2-3 года, сделайте выводы.
Решение.
Рассматриваем линейную
функцию
yt = a0 + a1 t.
Чтобы метод наименьших
квадратов дал простые расчётные формулы, моменты времени ti выбираем так, чтобы 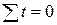 .
.
Тогда 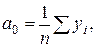
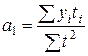 .
.
|
i
|
1
|
2
|
3
|
4
|
5
|
6
|
|
t
|
-5
|
-3
|
-1
|
1
|
3
|
5
|
|
y
|
933,4
|
904
|
965
|
1014,1
|
1064,8
|
1122,9
|
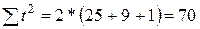
а0 =
а1 = 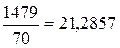
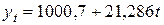
Для следующих трёх лет
вычисляем
у7 = 1149,7; у9
= 1192,3; у11 = 1234,8.

Вывод: на ближайшие годы
ожидается увеличение потерь рабочего времени в среднем на 3,7% ежегодно.
Задача 3. Имеются данные
по предприятиям отрасли:
Предприятия
|
Среднегодовая
стоимость производственных фондов, тыс. руб.
|
Прибыль,
тыс. руб.
|
|
Предыдущий
год
|
Отчётный
год
|
Предыдущий
год
|
Отчётный
год
|
|
1
|
10000
|
12500
|
2000
|
2400
|
|
2
|
7400
|
7800
|
1560
|
1820
|
Определите:
1)
индексы рентабельности производства для каждого предприятия в отдельности
(индивидуальные индексы);
2)
индексы рентабельности производства:
а)
переменного состава;
б)
фиксированного состава;
в)
структурных сдвигов.
Объясните
различие полученных результатов. Покажите взаимосвязь исчисленных индексов.
Сделайте выводы.
Решение.
Пусть р
– прибыль, q – стоимость производственных фондов.
1) для
индивидуального индекса
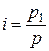 будет i1 = 1,2;
будет i1 = 1,2;  i2
= 1,17.
i2
= 1,17.
В этих
пределах будут заключены агрегатные индексы, которые мы будем вычислять, кроме
структурных сдвигов.
2)
индекс переменного состава
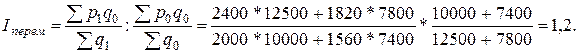
Индекс
фиксированного состава

Индекс
структурных сдвигов
I = Iперем : Iфикс = 1,009.
Индекс Iфикс не учитывает влияния структурных
сдвигов, индекс Iперем учитывает такое влияние, индекс структурных сдвигов показывает, в какую
сторону влияют эти структурные сдвиги (на повышение или на понижение). У нас
все индексы больше единицы, т.е. рентабельность повышается по всем критериям.
Задача
4. Оцените тесноту взаимной связи признаков «онкологическая
заболеваемость» и «работа со свинцом».
|
Работа со свинцом
|
Обследовано рабочих, чел
|
|
Всего
|
В том числе
|
|
Больные онкозаболеваемости
|
Здоровье
|
|
Да
|
36
|
28
|
8
|
|
Нет
|
144
|
62
|
82
|
|
Итого
|
180
|
90
|
90
|
Решение.
а = 28,
в = 8, с = 62, d = 82.
Коэффициент
контингенции
Кк
= 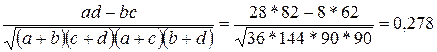 вопроса не решает,
поскольку не превысил значения 0,3.
вопроса не решает,
поскольку не превысил значения 0,3.
Коэффициент
ассоциации
Ка
= 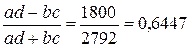 такую зависимость
зафиксировал, поскольку Ка превысил значение 0,5.
такую зависимость
зафиксировал, поскольку Ка превысил значение 0,5.
Задача
5. Имеются следующие данные по экономике страны (млрд. руб.):
|
Выпуск продуктов в основных ценах
|
3900
|
|
Выпуск рыночных услуг (за
исключение условно исчисленных услуг финансовых посредников)
|
1100
|
|
Выпуск не рыночных услуг
|
900
|
|
Налоги на продукты и услуги
|
790
|
|
Прочие косвенные налоги
|
310
|
|
Экспорт товаров и услуг
|
430
|
|
Импорт товаров и услуг
|
350
|
|
Проценты, получаемые банками по
ссудам
|
290
|
|
Проценты, уплаченные банками за
пользование средствами
|
165
|
|
Субсидии на импорт
|
45
|
|
Материальные затраты на
производство продуктов и услуг в течение года
|
2175
|
|
- износ основных средств
|
405
|
|
- недоамортизированная стоимость выбывших основных средств
|
45
|
|
Прочие элементы промежуточного
потребления (за исключением условно исчисленной продукции банков).
|
90
|
Определите
валовой внутренний продукт в рыночных ценах.
Решение.
ВВП =  где
где
ВДС –
валовая добавленная стоимость;
ЧН –
чистые налоги;
ПП –
промежуточное потребление;
Н –
налоги;
С –
субсидии на продукты и импорт.
ВВП =
(3900 + 1100 + 900 + 430) – (350 + 2175 + 405 + 90) + (790 + 310 + 290) – (165
+ 45) = 4445 млрд. руб.
Задача
6. Имеются следующие данные о распределении населения региона по 10% группам
населения по уровню среднедушевого дохода:
|
Базисный
|
Отчётный
|
|
Денежные доходы – всего
|
100,0
|
100,0
|
|
В том числе по 10% группам
населения
|
|
|
|
Первая (с наименьшими доходами)
|
2,3
|
2,1
|
|
Вторая
|
3,7
|
3,3
|
|
Третья
|
5,2
|
4,2
|
|
Четвёртая
|
6,4
|
5,8
|
|
Пятая
|
7,6
|
7,2
|
|
Шестая
|
10,0
|
8,9
|
|
Седьмая
|
12,2
|
8,9
|
|
Восьмая
|
14,3
|
12,5
|
|
Девятая
|
16,7
|
21,4
|
|
Десятая (с наибольшими доходами)
|
21,6
|
25,7
|
Определите
коэффициенты дифференциации доходов (коэффициент фондов), концентрация доходов
Джини.
Постройте
график Лоренца. Сделайте выводы.
Решение.
Коэффициент
фондов
Кф
= 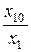
меняет
своё значение от 9,4 до 12,2, что говорит об усилении дифференциации доходов.
Более точную информацию об этом даст коэффициент Джини.
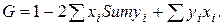
Вычислим
значения Sum yi.
|
Базисный период
|
Отчётный период
|
|
0,023
|
0,021
|
|
0,06
|
0,054
|
|
0,112
|
0,096
|
|
1,176
|
0,154
|
|
0,252
|
0,224
|
|
0,352
|
0,313
|
|
0,474
|
0,402
|
|
0,617
|
0,527
|
|
0,784
|
0,741
|
|
1
|
1
|
Далее,
все хi = 0,1; 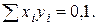
Теперь
вычисляем сумму 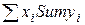 : получим 0,385 (базисный период); 0,3532 (отчётный).
: получим 0,385 (базисный период); 0,3532 (отчётный).
G = 0,33 (базисный), G = 0,39 (отчётный).
Первоначальный
вывод подтверждается. Вообще, 0 ≤ G ≤ 1. Чем ближе значение G к 1, тем сильнее концентрация
доходов.
Кривую
Лоренца построим для отчётного периода, поскольку расслоенность по доходам в
нём больше, шаг берём h = 0,2.
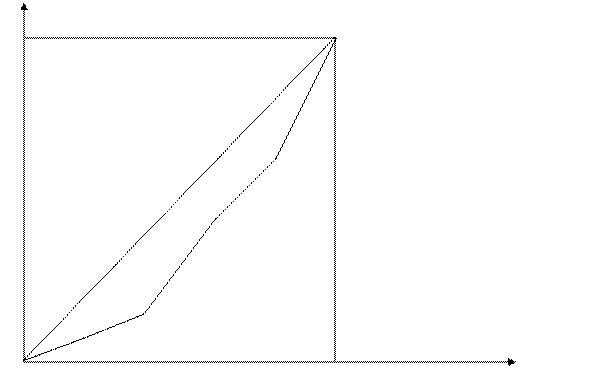
Задача 7. Предприятие работает
с 25 сентября. Численность работников списочного состава была следующей:
25 сентября (вторник) –
180 чел;
26 сентября (среда) – 185
чел;
27 сентября (четверг) –
200 чел;
28 сентября (пятница) –
210 чел.
Последние два дня месяца
приходились на выходные дни.
Кроме того, известно, что
число совместителей с 25 по27 – 5 чел; с
28 по 30 – 7 чел; а число работающих по договорам гражданско-правового
характера с 25 по 27 сентября – 10 чел; и с 28 по 30 – 12 чел.
Среднесписочная
численность за октябрь – 180 чел; за ноябрь – 175 чел. В декабре число явок на
работу составило 3960 человеко-дней, число неявок по всем причинам 1800
человеко-дней.
Определите
среднесписочную численность работников за год.
Решение.
Вычисляем 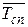 за сентябрь.
за сентябрь.
Для обычных работников
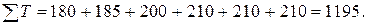
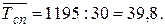
Для совместителей
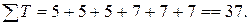
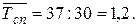
Для работников по
договорам
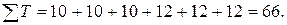
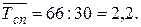
В целом за сентябрь
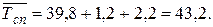
В декабре для работников
человеко-дней получилось
3960 + 1800 = 5760
чел.-дней.
Рабочих дней в декабре 31
– 9 = 22.
Значит, 
За год 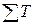 = 43,2*30 + 180*31 + 175*30 + 261,8*31 = 20541,8.
= 43,2*30 + 180*31 + 175*30 + 261,8*31 = 20541,8.
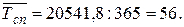
Список литературы
1.
Айвазян С.А., Мхитарян В.С. Прикладная
статистика. – М.: Финансы и статистика, 1998.
2.
Башкатова Б.И. Социально
экономическая статистика. – М.: Инфра-М, 2002.
3.
Елисеева И.И. Общая
теория статистики. – М.: Финансы и статистика, 1996.
4.
Жафяров А.Ж., Малыгин А.В. Проверка
статистических гипотез. – Новосибирск: НГПУ, 2001.
5.
Яковлев Р.Д. Общая теория
статистики. – М.:, Юнити-Дана, 2004.