ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОУ ВПО ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-КОНОМИЧЕСКИЙ ИНСТИТУТ
КОНТРОЛЬНАЯ РАБОТА ПО ДИСЦИПЛИНЕ:
ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ И
ПРИКЛАДНЫЕ МОДЕЛИ
ВАРИАНТ 2
ВЫПОЛНИЛА:
СТУДЕНТКА
III КУРСА (ДНЕВНАЯ Ф/О)
ФАКУЛЬТЕТ: ФИНАНСОВО-КРЕДИТНЫЙ
СПЕЦИАЛЬНОСТЬ: ФИНАНСЫ И
КРЕДИТ
ПРЕПОДАВАТЕЛЬ: КНЯЗЕВА И.В.
г. Калуга, 2007г.
Задание 1
Совхоз для кормления животных использует два вида корма. В
дневном рационе животного должно содержаться не менее 6 единиц питательного
вещества А и не менее 12 единиц
питательного вещества В. Какое количество корма надо расходовать ежедневно на
одно животное, чтобы затраты были минимальными?
|
Питательное
вещество
|
Количество
питательных веществ в 1 кг
корма
|
|
1
|
2
|
|
А
|
2
|
1
|
|
В
|
2
|
4
|
|
Цена
1 кг
корма, тыс.руб.
|
0,2
|
0,3
|
Построить экономико-математическую модель задачи, дать
необходимые комментарии к ее элементам и получить решение графическим методом.
Что произойдет, если решить задачу на максимум и почему?
Решение
Пусть:
х1 – количество корма «1»
х2 – количество корма «2»
|
Целевая функция:
|
|
|
min z = 0,2 ∙ x1
+ 0,3 ∙ x2
|
т.е. необходим минимум затрат на
корма
|
|
2 ∙ x1 + x2 ≥ 6
|
т.е. из всего объема потребляемых
кормов, вещества «А» должно быть не менее 6 единиц
|
|
2 ∙ x1 + 4 ∙ x2 ≥ 12
|
т.е. из всего объема потребляемых
кормов, вещества «А» должно быть не менее 6 единиц
|
|
x1; x2 ≥ 0
|
Количество потребляемых кормов не
может быть отрицательным
|
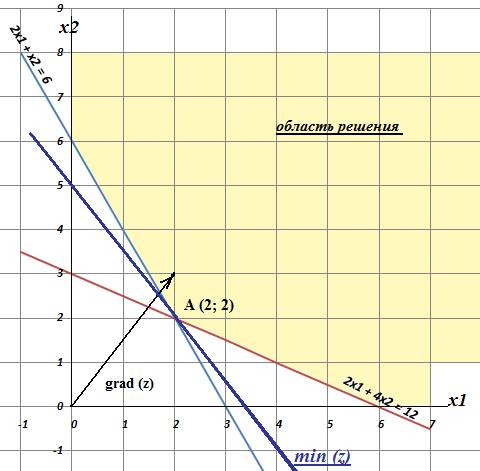
Определим по графику минимальное значение функции z:
|
2 ∙
x1 + x2 = 6
|
|
2 ∙
x1 + 4 ∙ x2 = 12
|
Решение системы: x1 =2
x2 = 2
Минимальные затраты: z = 0,2 ∙ 2 + 0,3 ∙ 2 = 1
Таким образом, минимальные затраты на корм составляют 1
тыс.руб. и возможны при использовании 2 ед. корма «А» и 2 ед. корма «Б».
Решение задачи на максимум приведет к решению +∞, т.к
график сверху справа не ограничен.
Задача 2
Для изготовления четырех видов продукции используют три вида
сырья. Запасы сырья, нормы его расхода и цены реализации единицы каждого вида
продукции приведены в таблице.
|
Тип
сырья
|
Нормы
расхода сырья на одно изделия
|
Запасы
сырья
|
|
А
|
Б
|
В
|
Г
|
|
I
|
1
|
0
|
2
|
1
|
180
|
|
II
|
0
|
1
|
3
|
2
|
210
|
|
III
|
4
|
2
|
0
|
4
|
800
|
|
Цена
изделия
|
9
|
6
|
4
|
7
|
|
1.
Сформулируем прямую оптимизационную задачу на
максимум выручки от реализации готовой продукции, получить оптимальный план
выпуска продукции.
Пусть xi
, i = {1, .. 4} –
количество соответственно ресурсов «А», «Б», «В», «Г».
Max f(x) = 9 ∙ x1 + 6 ∙ x2 + 4 ∙ x3 + 7 ∙ x4
1 ∙ x1
+ 0 ∙ x2
+ 2 ∙ x3
+ 1 ∙ x4 ≤ 180
0 ∙ x1
+ 1 ∙ x2
+ 3 ∙ x3
+ 2 ∙ x4 ≤ 210
4 ∙ x1
+ 2 ∙ x2
+ 0 ∙ x3
+ 4 ∙ x4 ≤ 800
xi
≥0 , i = {1, .. 4}
Решим задачу, используя пакет анализа «Поиск решения»
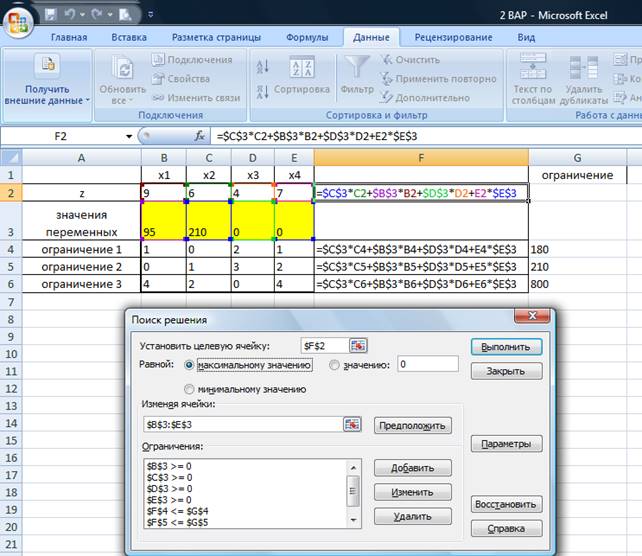
Таким образом, функция достигает максимального значения при
x1
=95
x2
= 210
x3
= 0
x4
= 0
max f(x) = 2115
2.
Сформулируйте двойственную задачу и найти ее
оптимальный план с помощью теорем двойственности.
Двойственная задача имеет вид:
Min f(y) = 180 ∙ y1 + 210 ∙ y2 + 800 ∙ y3
1 ∙ y1
+ 0 ∙ y2
+ 4 ∙ y3
≥ 9
0 ∙ y1
+ 1 ∙ y2
+ 2 ∙ y3
≥ 6
2 ∙ y1
+ 3 ∙ y2
+ 0 ∙ y3
≥ 4
1 ∙ y1
+ 2 ∙ y2
+ 4 ∙ y3
≥ 7
yi
≥0 , i = {1, ..
3}
Найдем значения двойственных переменных, используя теоремы
двойственности.
Проверим, как удовлетворяется система функциональных
ограничений оптимальным планом:
|
у1 :
|
1 ∙ 95 + 0 ∙ 210 + 2
∙ 0 + 1 ∙ 0 =
95 ≤ 180
|
|
у2 :
|
0 ∙ 95 + 1 ∙ 210 + 3
∙ 0 + 2 ∙ 0 =
210
|
|
у3 :
|
4 ∙ 95 + 2 ∙ 210 + 0
∙ 0 + 4 ∙ 0 =
800
|
Так как первое ограничение выполняется как строгое
неравенство, то
у1 = 0.
Учитывая, что x1 ≥ 0 ; x2 ≥ 0, то значения остальных двойственных
переменных найдем из 1 и 2-го уравнений системы неравенств. То есть
|
{
|
1
∙ y1
+ 0 ∙ y2
+ 4 ∙ y3
= 9
|
|
0
∙ y1
+ 1 ∙ y2
+ 2 ∙ y3
= 6
|
у1 = 0;
у3 = 9 / 4 = 2,25;
у2 = 6 – 2 ∙ 2,25 = 1,5.
Рассчитаем значение целевой функции двойственной задачи
Min f(y) = 180 ∙ 0 + 210
∙ 1,5 + 800 ∙ 2,25 = 2115.
3.
Пояснить нулевые значения переменных в оптимальном
плане.
Если стоимость ресурсов, затраченных на производство одного
изделия, больше его цены, то это изделие не войдет в оптимальный план из-за
своей убыточности. В нашей задаче это изделие В и Г. Подтвердим этот факт,
подставим в ограничения двойственной задачи оптимальные значения вектора Y.
1 ∙ 0 + 0 ∙ 1,5 + 4 ∙ 2,25 = 9
0 ∙ 0 + 1 ∙ 1,5 + 2 ∙ 2,25 = 6
2 ∙ 0 + 3 ∙ 1,5 + 0 ∙ 2,25 =4,5 ≥ 4
1 ∙ 0 + 2 ∙ 1,5 + 4 ∙ 2,25 =12 ≥ 7
4.
На основе двойственных оценок и теорем
двойственности:
а)
Поясним использование ресурсов в оптимальном
плане исходной задачи.
В оптимальном плане не полностью используется сырье 1, т.к.
у1 = 0
Сырье 2 и 3 – дефицитное, т.к. их двойственные оценки
отличны от нуля.
б)
При увеличении сырья 2 на 120 ед, сырья 3 – на
160 ед, и уменьшении сырья 1 на 60 ед. произойдут следующие изменения:
Увеличение
сырья 2 на 120 ед. приведет к увеличению выручки на
120 ∙ у2 = 120 ∙ 1,5 = 180 ед.
Увеличение сырья 3 на 160 ед. приведет к увеличению выручки
на
160 ∙ у3 = 160 ∙ 2,25 = 360 ед.
Увеличение сырья 1 на 60 ед. не повлияет на оптимальный
план, так как
у1 = 0
Таким образом, общее изменение выручки составит:
∆ = 180 + 360 + 0 = 540 ед.
в) оценим целесообразность внедрения изделия ∆ ценой
12 единиц, на изготовление которого расходуется по две единицы каждого сырья.
2 ∙ 0 + 2 ∙ 1,5 + 2 ∙ 2,25 – 12 = -4,5
< 0 à
целесообразно.
Задача 3
В течение девяти последовательных недель фиксировался спрос Y(t) (млн.руб.) на кредитные ресурсы
финансовой компании.
Построим линейную модель Yr(t)
= a0 + a1 ∙ t, параметры которой оценим с
помощью МНК.
a1 = ∑ (xi
– xcr) ∙ (yi – ycr) / ∑ (xi
– xcr)2
a0 = ycr – a1 ∙ xcr
Составим разработочную таблицу:
|
х
|
у
|
(yi
– ycr)
|
(xi
– xcr)
|
(xi
– xcr)2
|
(xi
– xcr) ∙ (yi – ycr)
|
|
1
|
43
|
-10,778
|
-4
|
16
|
43,111
|
|
2
|
47
|
-6,778
|
-3
|
9
|
20,333
|
|
3
|
50
|
-3,778
|
-2
|
4
|
7,556
|
|
4
|
48
|
-5,778
|
-1
|
1
|
5,778
|
|
5
|
54
|
0,222
|
0
|
0
|
0,000
|
|
6
|
57
|
3,222
|
1
|
1
|
3,222
|
|
7
|
61
|
7,222
|
2
|
4
|
14,444
|
|
8
|
59
|
5,222
|
3
|
9
|
15,667
|
|
9
|
65
|
11,222
|
4
|
16
|
44,889
|
|
Сумма
|
45
|
484
|
0,000
|
0
|
60
|
155,000
|
|
Среднее
|
5
|
53,778
|
0,000
|
0
|
6,667
|
17,222
|
Отсюда
a1
= 155 / 60 = 2,583
a0
= 53,778 – 2,583 ∙ 5 = 40,861
Таким образом, линейная модель имеет вид:
Yr(t) = 40,861 + 2,583 ∙ t
1.
Построим адаптивную модель Брауна
По первым пяти точкам ряда оцениваем значения а1
и а0 параметров модели с помощью МНК
|
х
|
у
|
уi - ycr
|
xi - xcr
|
(xi - xcr)2
|
(xi-xcr)∙(yi-ycr)
|
|
1
|
43
|
-5,400
|
-2
|
4
|
10,800
|
|
2
|
47
|
-1,400
|
-1
|
1
|
1,400
|
|
3
|
50
|
1,600
|
0
|
0
|
0,000
|
|
4
|
48
|
-0,400
|
1
|
1
|
-0,400
|
|
5
|
54
|
5,600
|
2
|
4
|
11,200
|
|
Итого
|
242
|
0,000
|
0
|
10
|
23,000
|
|
Среднее
|
48,4
|
0,000
|
0
|
2
|
4,600
|
Получаем
a1
= 23 / 10 = 2,3
a0
= 48,4 - 2,3 ∙ 3 = 41,5
которые соответствуют моменту времени t=0
Прогноз на первый шаг у1расч = а0(0) +
а1(0) = 2,3 + 41,5 = 43,8
Величина отклонения: е = 43 – 43, 8 = -0, 8
Корректируем параметры (α = 0,4; β = 0,6)
a0(t)
= a0(t-1) + a1(t-1) + (1 – β2) ε (t) = 41,5 + 2,3 + (1 – 0,62)
∙ (-0, 8) = 43,288
a1(t)
= a1(t-1) + (1 – β) 2 ε (t) = 2,3 + (1 – 0,6) 2 ∙ (-0, 8)
= 2,172
Далее расчеты производятся аналогично (см. таблицу)
|
t
|
y
|
a0
|
a1
|
yr
|
ε
|
|
0
|
|
41,500
|
2,300
|
|
|
|
1
|
43
|
43,288
|
2,172
|
43,800
|
-0,800
|
|
2
|
47
|
46,446
|
2,418
|
45,460
|
1,540
|
|
3
|
50
|
49,591
|
2,600
|
48,864
|
1,136
|
|
4
|
48
|
49,509
|
1,930
|
52,191
|
-4,191
|
|
5
|
54
|
53,078
|
2,339
|
51,438
|
2,562
|
|
6
|
57
|
56,430
|
2,593
|
55,417
|
1,583
|
|
7
|
61
|
60,288
|
2,909
|
59,023
|
1,977
|
|
8
|
59
|
60,511
|
2,237
|
63,197
|
-4,197
|
|
9
|
65
|
64,189
|
2,598
|
62,748
|
2,252
|
Аналогичные расчеты для α = 0,7; β = 0,3
|
t
|
y
|
a0
|
a1
|
yr
|
ε
|
|
0
|
|
41,500
|
2,300
|
|
|
|
1
|
43
|
43,072
|
1,908
|
43,800
|
-0,800
|
|
2
|
47
|
46,818
|
2,898
|
44,980
|
2,020
|
|
3
|
50
|
49,974
|
3,037
|
49,716
|
0,284
|
|
4
|
48
|
48,451
|
0,581
|
53,011
|
-5,011
|
|
5
|
54
|
53,553
|
3,015
|
49,032
|
4,968
|
|
6
|
57
|
56,961
|
3,227
|
56,568
|
0,432
|
|
7
|
61
|
60,927
|
3,625
|
60,188
|
0,812
|
|
8
|
59
|
59,500
|
0,904
|
64,552
|
-5,552
|
|
9
|
65
|
64,586
|
3,156
|
60,404
|
4,596
|
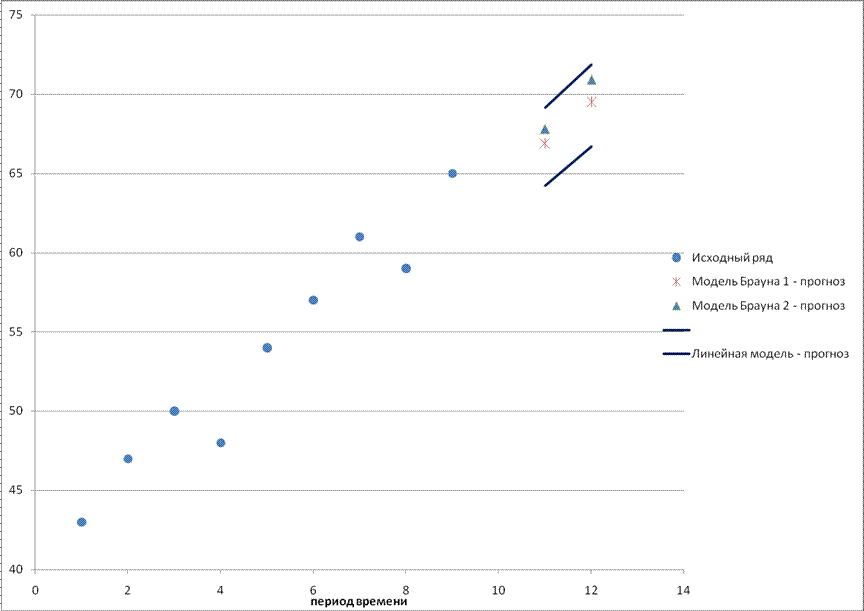
Графики построенных моделей представлены на рисунке:
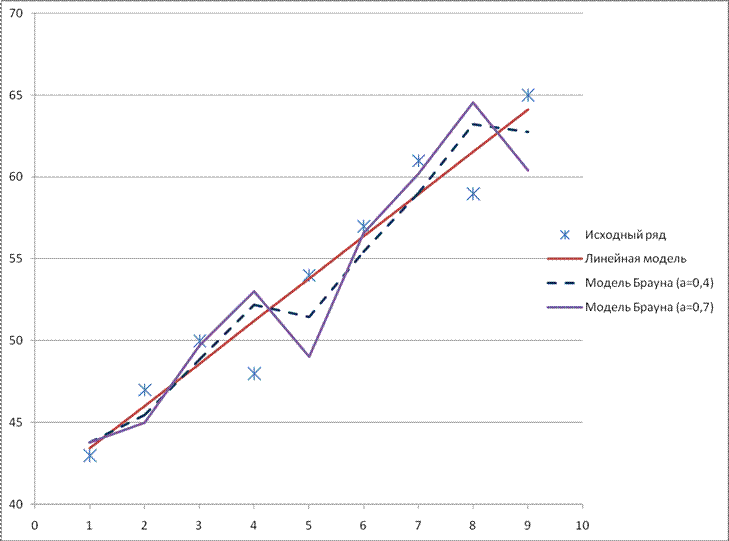
Рисунок 1
Временной ряд и построенные модели
Проведем качества каждой из моделей.
Для линейной модели:
Анализ остатков
|
х
|
у
|
yr
|
ε
|
Точки поворота
|
ε 2
|
yi-ycr
|
(yi-ycr)2
|
ε / y
|
|
1
|
43
|
43,444
|
-0,444
|
|
0,198
|
-10,778
|
116,160
|
1,034
|
|
2
|
47
|
46,028
|
0,972
|
|
0,945
|
-6,778
|
45,938
|
2,069
|
|
3
|
50
|
48,611
|
1,389
|
*
|
1,929
|
-3,778
|
14,272
|
2,778
|
|
4
|
48
|
51,194
|
-3,194
|
*
|
10,204
|
-5,778
|
33,383
|
6,655
|
|
5
|
54
|
53,778
|
0,222
|
|
0,049
|
0,222
|
0,049
|
0,412
|
|
6
|
57
|
56,361
|
0,639
|
|
0,408
|
3,222
|
10,383
|
1,121
|
|
7
|
61
|
58,944
|
2,056
|
*
|
4,225
|
7,222
|
52,160
|
3,370
|
|
8
|
59
|
61,528
|
-2,528
|
*
|
6,390
|
5,222
|
27,272
|
4,284
|
|
9
|
65
|
64,111
|
0,889
|
|
0,790
|
11,222
|
125,938
|
1,368
|
|
Итого
|
484
|
|
|
4
|
25,139
|
|
425,556
|
23,089
|
|
Среднее
|
53,778
|
|
|
|
|
|
|
2,565
|
Критерий случайности отклонений от тренда при уровне
вероятности 0,95 можно представить как
Р>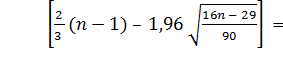
Учитывая, что неравенство выполняется, то есть 4 > 3 –
модель адекватна
Рассчитаем коэффициент детерминации по формуле:
Коэффициент детерминации:
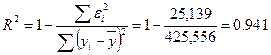
Значение коэффициента F–критерия Фишера:
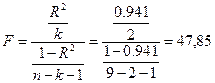
Табличное значение коэффициента F–критерия Фишера равно 5,14
и поскольку Fрас>Fтаб, уравнение регрессии
следует признать адекватным.
Проверим соответствие ряда
остатков нормальному распределению по RS-критерию.
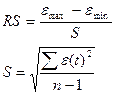
ε max = 2,056
ε min = -3,194
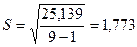
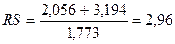
Учитывая, что полученное значение RS критерия попадает в интервал от 2,7 до
3,7, то уровни ряда остатков подчиняются нормальному закону распределения.
Средняя относительная ошибка аппроксимации:
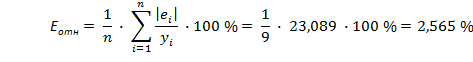
Еотн = 2,565 < 7,
что свидетельствует о хорошем качестве модели.
Модель Брауна 1:
Анализ остатков
|
х
|
у
|
yr
|
ε
|
Точки поворота
|
ε 2
|
yi-ycr
|
(yi-ycr)2
|
ε / y
|
|
1
|
43
|
43,288
|
-0,288
|
|
0,083
|
-10,778
|
116,160
|
0,670
|
|
2
|
47
|
46,446
|
0,554
|
*
|
0,307
|
-6,778
|
45,938
|
1,180
|
|
3
|
50
|
49,591
|
0,409
|
|
0,167
|
-3,778
|
14,272
|
0,818
|
|
4
|
48
|
49,509
|
-1,509
|
*
|
2,277
|
-5,778
|
33,383
|
3,143
|
|
5
|
54
|
53,078
|
0,922
|
*
|
0,850
|
0,222
|
0,049
|
1,708
|
|
6
|
57
|
56,430
|
0,570
|
*
|
0,325
|
3,222
|
10,383
|
1,000
|
|
7
|
61
|
60,288
|
0,712
|
*
|
0,507
|
7,222
|
52,160
|
1,167
|
|
8
|
59
|
60,511
|
-1,511
|
*
|
2,283
|
5,222
|
27,272
|
2,561
|
|
9
|
65
|
64,189
|
0,811
|
|
0,657
|
11,222
|
125,938
|
1,247
|
|
Итого
|
484
|
|
|
6
|
7,456
|
|
425,556
|
13,493
|
|
Среднее
|
53,778
|
|
|
|
|
|
|
1,499
|
Критерий случайности отклонений от тренда при уровне
вероятности 0,95 можно представить как
Р>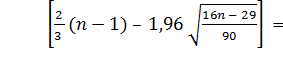
Учитывая, что неравенство выполняется, то есть 6 > 3 –
модель адекватна
Рассчитаем коэффициент детерминации по формуле:
Коэффициент детерминации:
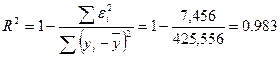
Значение коэффициента F–критерия Фишера:
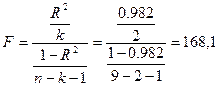
Табличное значение коэффициента F–критерия Фишера равно 5,14
и поскольку Fрас>Fтаб, уравнение регрессии
следует признать адекватным.
Проверим соответствие ряда
остатков нормальному распределению по RS-критерию.
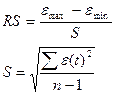
ε max = 0,922
ε min = -1,511
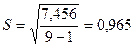
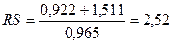
Учитывая, что полученное значение RS критерия достаточно близко к интервалу от 2,7 до 3,7, то уровни ряда
остатков подчиняются нормальному закону распределения.
Средняя относительная ошибка аппроксимации:
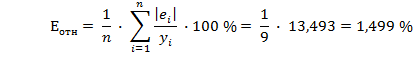
Еотн = 1,499 < 7,
что свидетельствует о хорошем качестве модели.
Модель Брауна 2:
Анализ остатков
|
х
|
у
|
yr
|
ε
|
Точки поворота
|
ε 2
|
yi-ycr
|
(yi-ycr)2
|
ε / y
|
|
1
|
43
|
43,800
|
-0,800
|
|
0,640
|
-10,778
|
116,160
|
1,860
|
|
2
|
47
|
44,980
|
2,020
|
*
|
4,080
|
-6,778
|
45,938
|
4,298
|
|
3
|
50
|
49,716
|
0,284
|
|
0,081
|
-3,778
|
14,272
|
0,568
|
|
4
|
48
|
53,011
|
-5,011
|
*
|
25,114
|
-5,778
|
33,383
|
10,440
|
|
5
|
54
|
49,032
|
4,968
|
*
|
24,677
|
0,222
|
0,049
|
9,199
|
|
6
|
57
|
56,568
|
0,432
|
*
|
0,186
|
3,222
|
10,383
|
0,757
|
|
7
|
61
|
60,188
|
0,812
|
*
|
0,659
|
7,222
|
52,160
|
1,331
|
|
8
|
59
|
64,552
|
-5,552
|
*
|
30,822
|
5,222
|
27,272
|
9,410
|
|
9
|
65
|
60,404
|
4,596
|
|
21,122
|
11,222
|
125,938
|
7,071
|
|
Итого
|
484
|
|
|
6
|
107,382
|
|
425,556
|
44,934
|
|
Среднее
|
53,778
|
|
|
|
|
|
|
4,993
|
Критерий случайности отклонений от тренда при уровне
вероятности 0,95 можно представить как
Р>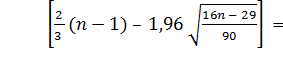
Учитывая, что неравенство выполняется, то есть 6 > 3 –
модель адекватна
Рассчитаем коэффициент детерминации по формуле:
Коэффициент детерминации:
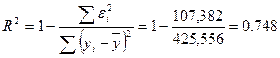
Значение коэффициента F–критерия Фишера:
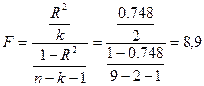
Табличное значение коэффициента F–критерия Фишера равно 5,14
и поскольку Fрас>Fтаб, уравнение регрессии
следует признать адекватным.
Проверим соответствие ряда
остатков нормальному распределению по RS-критерию.
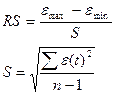
ε max = 4,968
ε min = -5,552
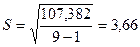
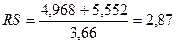
Учитывая, что полученное значение RS критерия попадает в интервал от 2,7
до 3,7, то уровни ряда остатков подчиняются нормальному закону распределения.
Средняя относительная ошибка аппроксимации:
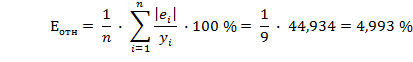
Еотн = 4,993 < 7,
что свидетельствует о достаточно хорошем качестве мо
Все из представленных моделей
адекватны, о чем свидетельствует анализ остатков моделей.
Наиболее точная модель – модель
Брауна, о чем говорит самой низкое значение коэффициента аппроксимации.
Построим прогноз спроса на следующие две недели на основе построенных
моделей.
Линейная модель:
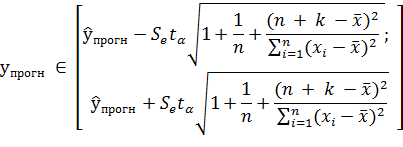
При вероятности 0,7 tα = 1,119
1) При
t=10
 (10)= 40,861 + 2,583 ∙ 10 = 66,691
(10)= 40,861 + 2,583 ∙ 10 = 66,691
Нижняя граница:
унижн = 66,691 – 1,773 ∙ 1,119 ∙ 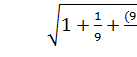 = 66,691 – 2,452 = 64,239
= 66,691 – 2,452 = 64,239
Верхняя граница:
унижн = 66,691 + 1,773 ∙ 1,119 ∙ 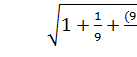 = 66,691 + 2,452 = 69,143
= 66,691 + 2,452 = 69,143
2) При
t=11
 (11)= 40,861 + 2,583 ∙ 11 = 69,274
(11)= 40,861 + 2,583 ∙ 11 = 69,274
Нижняя граница:
унижн = 69,274 – 1,773 ∙ 1,119 ∙ 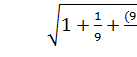 = 69,274 – 2,595 = 66,679
= 69,274 – 2,595 = 66,679
Верхняя граница:
унижн = 69,274 + 1,773 ∙ 1,119 ∙ 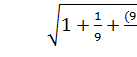 = 69,274 + 2,595 = 71,869
= 69,274 + 2,595 = 71,869
Модель Брауна 1:
1) При
t=10
 (10)= а0(9) + а1(9)
∙ 1 = 64,189 + 2,589 ∙ 1 = 66,778
(10)= а0(9) + а1(9)
∙ 1 = 64,189 + 2,589 ∙ 1 = 66,778
2) При
t=11
 (11)= а0(9) + а1(9)
∙ 2 = 64,189 + 2,589 ∙ 2 = 69,367
(11)= а0(9) + а1(9)
∙ 2 = 64,189 + 2,589 ∙ 2 = 69,367
Модель Брауна 2:
3) При
t=10
 (10)= а0(9) + а1(9)
∙ 1 = 64,586 + 3,156 ∙ 1 = 67,742
(10)= а0(9) + а1(9)
∙ 1 = 64,586 + 3,156 ∙ 1 = 67,742
4) При
t=11
 (11)= а0(9) + а1(9)
∙ 2 = 64,586 + 3,156 ∙ 2 = 70,898
(11)= а0(9) + а1(9)
∙ 2 = 64,586 + 3,156 ∙ 2 = 70,898