ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ГОУ ВПО
ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
ЯРОСЛАВСКИЙ ФИЛИАЛ
Контрольная
работа
по
дисциплине «Эконометрика»
Вариант №20
|
Выполнил:
|
Мокрова Наталья Григорьевна
|
|
Факультет:
|
ФК
|
|
Специальность:
|
ФК
|
|
Курс
|
III
|
|
Форма обучения
|
2ВО
|
|
Зачетная книжка
|
08ФФД62370
|
|
Проверил:
|
ДОЦ.
|
Д.И. Асеев
|
Ярославль 2009
Задание I.
Таблица
1
Значения
исходных данных
|
t
|
y
|
|
1
|
50
|
|
2
|
52
|
|
3
|
54
|
|
4
|
59
|
|
5
|
57
|
|
6
|
60
|
|
7
|
63
|
|
8
|
68
|
|
9
|
70
|
1)
определить наличие тренда Y(t);
2)
построить линейную модель 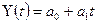 , параметры которой оценить с помощью МНК;
, параметры которой оценить с помощью МНК;
3)
оценить адекватность построенной модели на основе
исследования:
·
случайности остаточной компоненты по критерию пиков;
·
независимости уровней ряда остатков по d-критерию (в качестве
критических использовать уровни  и
и 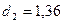 ) или по первому коэффициенту корреляции, критический
уровень которого r(1) = 0,36;
) или по первому коэффициенту корреляции, критический
уровень которого r(1) = 0,36;
·
нормальности распределения остаточной компоненты
по R/S-критерию с
критическими уровнями 2,7 – 3,7;
4)
для оценки точности модели использовать
среднеквадратическое отклонение и среднюю по модулю относительную ошибку;
5)
построить точечный и интервальный прогнозы на два шага
вперед (для вероятности Р=70% используйте коэффициент
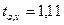 ;
;
Решение.
1. Определение наличия тренда Y(t)
Динамический ряд Y(t) является временным, так как изменение экономического
показателя Y происходит
в зависимости от времени t.
Если во временном ряду проявляется длительная
тенденция изменения экономического показателя, то в этом случае говорят о
наличии тренда.
Под трендом понимается изменение, определяющее
общее направление развития, т.е. основная тенденция изменения временного ряда.
Для определения тренда в исходном временном ряду
применяем метод проверки разностей средних уровней. Разобьем динамический ряд Y(t) на две части, каждая из которых
представляет собой самостоятельную выборочную совокупность, имеющую нормальное
распределение:
(Y1…Y4) – n1 = 4,
(Y5…Y9) – n2 = 5,
где
Y1…Y5 - уровни ряда;
n1, n2 -
число уровней ряда.
Таблица 2
Группы динамического ряда
|
t
|
y
|
|
5
|
57
|
|
6
|
60
|
|
7
|
63
|
|
8
|
68
|
|
9
|
70
|
Принимаем нулевую гипотезу о равенстве средних
уровней двух нормально распределенных совокупностей. По каждой части ряда
рассчитаем значение среднего уровня и дисперсию.
Значения
средних уровней рассчитаем по формулам:
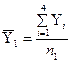 ,
,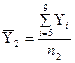 .
.
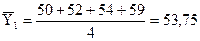 ;
; 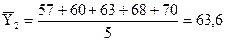
Дисперсии
ля каждой части ряда рассчитаем по формулам:
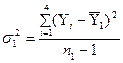 ,
, 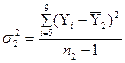 .
.
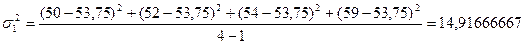 .
.
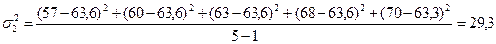
Проверяем однородность
дисперсии для первой и второй групп наблюдения. Рассчитаем F-критерий Фишера по формуле:
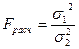 ;
; 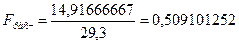 .
.
По таблице «Значения F-критерия Фишера при уровне значимости a = 0,05» определяем табличное
значение критерия Фишера 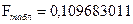 . Поскольку
. Поскольку 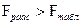 ( 0,5>0,1, дисперсии
не однородны (статистически не равны),т.е. различаются значительно, и расхождение между ними носит
закономерный характер.
( 0,5>0,1, дисперсии
не однородны (статистически не равны),т.е. различаются значительно, и расхождение между ними носит
закономерный характер.
Проверяем
гипотезу о равенстве средних уровней (отсутствие тренда): 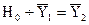 .
.
Рассчитаем среднее квадратическое отклонение для
всего ряда по формуле:
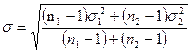 ,
, 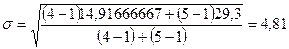 .
.
Рассчитаем
t-критерий Стьюдента по
формуле:
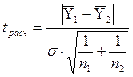 ,
, 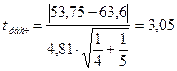
По таблице «Значения t-критерия Стьюдента при уровне
значимости 0,05» на основе заданной вероятности 0,95 и числа степеней свободы n-2 (9-2=7) определяем
табличное значение t-критерия Стьюдента: 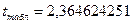 . Расчетное значение превышает табличное, следовательно
нулевая гипотеза отвергается.
. Расчетное значение превышает табличное, следовательно
нулевая гипотеза отвергается.
Определение наличия тренда в исходном временном
ряду можно осуществить с помощью Пакета анализа данных в MS Excel
Производим
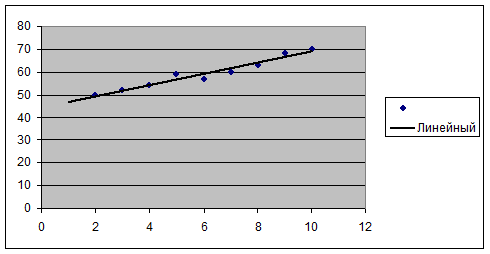
ввод исходных данных. На основании исходных данных строим поле корреляции и
добавляем линию тренда (рис.1):
- в главном меню выбираем, Вставка/Диаграмма и строим поле
корреляции;
- в области построения диаграммы
выделяем график, нажимаем правую кнопку мыши и из контекстного меню
выбираем команду Добавить линию
тренда;
 в
диалоговом окне Линия тренда на
вкладке Тип выбираем Линейная, на вкладке Параметры выбираем Показывать уравнение на диаграмме
и Поместить на диаграмму величину достоверности
аппроксимации
в
диалоговом окне Линия тренда на
вкладке Тип выбираем Линейная, на вкладке Параметры выбираем Показывать уравнение на диаграмме
и Поместить на диаграмму величину достоверности
аппроксимации  .
.
Рис.1. Определение наличия тренда.
Из графика динамического ряда Y(t) видно наличие возрастающей тенденции, что может
свидетельствовать о возможности существования линейного тренда.
Для определения наличия тренда в исходном
временном ряду применяем метод проверки разностей средних уровней, для чего разбиваем
динамический ряд Y(t) на две самостоятельно
выбранные совокупности (Рис. 2).
С помощью Пакета анализа данных в MS Excel определяем
F-критерий Фишера и
проводим двухвыборочный t-тест с одинаковыми
дисперсиями.
Для этого:
·
в главном меню выбираем Сервис/Анализ данных/ Двухвыборочный F-тест для
дисперсии (рис.2). Щелкаем по кнопке ОК.
·
заполняем формы в диалоговом окне Двухвыборочный F-тест для
дисперсии (рис. 3): интервал
переменной 1 - $B$3:$В$6 , интервал переменной 2 -$В$7:$В$11;
уровень значимости Альфа 0,05.
Щелкаем ОК.
Получаем
результаты расчета Двухвыборочного F-теста для дисперсии (табл. 3).
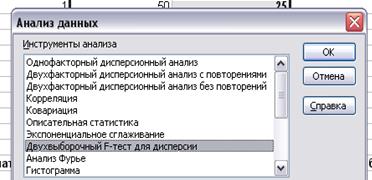
Рис.2. Анализ
данных Двухвыборочный F-тест
для дисперсии.
Рис. 3.
Двухвыборочный F-тест
для дисперсии
Таблица 3
Двухвыборочный
F-тест для дисперсии
|
|
Переменная 1
|
Переменная 2
|
|
Среднее
|
53,75
|
63,6
|
|
Дисперсия
|
14,91666667
|
29,3
|
|
Наблюдения
|
4
|
5
|
|
df
|
3
|
4
|
|
F
|
0,509101251
|
|
|
P(F<=f)
одностороннее
|
0,3029232
|
|
|
F
критическое одностороннее
|
0,109683011
|
|
Сравниваем
значение F=0,509 c критическим
значением F=0,109 т.к. F=0,509 больше, чем F критическая, то дисперсия не однородная.
Аналогично
с помощью Пакета анализа данных в MS Excel проводим двухвыборочный
t-тест с одинаковыми дисперсиями:
·
в главном меню выбираем Сервис/Анализ данных/Двухвыборочный t-тест с
одинаковыми дисперсиями (рис.4). Щелкаем по кнопке ОК.
Рис.4. Анализ
данных Двухвыборочный t-тест
с одинаковыми дисперсиями.
·
заполняем формы в диалоговом окне Двухвыборочный t-тест с
одинаковыми дисперсиями (рис.5): интервал
переменной 1-$В$3:$В$6, интервал переменной 2 - $В$7:$В$11; уровень
значимости Альфа 0,05. Щелкаем по
кнопке ОК.
Рис. 5
Двухвыборочный t-тест с
одинаковыми дисперсиями
Сравниваем средние значения полученные в двух
группах.
Таблица 4
Двухвыборочный t-тест с одинаковыми дисперсиями
|
|
Переменная 1
|
Переменная 2
|
|
Среднее
|
53,75
|
63,6
|
|
Дисперсия
|
14,91666667
|
29,3
|
|
Наблюдения
|
4
|
5
|
|
Объединенная
дисперсия
|
23,13571429
|
|
|
Гипотетическая
разность средних
|
0
|
|
|
df
|
7
|
|
|
t-статистика
|
-3,052730863
|
|
|
P(T<=t)
одностороннее
|
0,009255944
|
|
|
t
критическое одностороннее
|
1,894578604
|
|
|
P(T<=t)
двухстороннее
|
0,018511887
|
|
|
t
критическое двухстороннее
|
2,364624251
|
|
Вывод:
рассчитанное значение t-критерия по модулю приблизительно равно 3, а табличное
значение t-критерия Стьюдента равно приблизительно 2,36. Расчетное значение
больше табличного, и среднее значение в группах отличается существенно друг от
друга, т.е. признается наличие тренда.
2.
Построение линейной модели 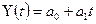
Линейная
модель регрессии описывается уравнением вида:
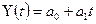 ,
,
где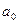 - постоянная
величина (свободный член уравнения);
- постоянная
величина (свободный член уравнения);
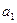 - коэффициент регрессии.
- коэффициент регрессии.
Построение
этой модели сводится к определению параметров 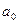 и
и 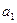 по существующим
исходным данным.
по существующим
исходным данным.
Классический
подход при определении параметров 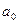 и
и 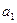 , при которых сумма квадратов отклонений фактических
значений
, при которых сумма квадратов отклонений фактических
значений  от расчетных
от расчетных 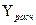 была бы минимальной:
была бы минимальной:
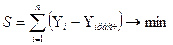 ,
,
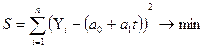
Таким образом, решается задача оптимизации:
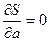 и
и 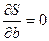 .
.
Исходя из этих двух условий, получается
система нормальных уравнений:
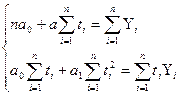 .
.
Откуда
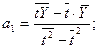
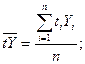
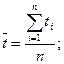
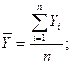
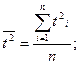
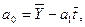
где 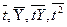 - средние значения;
- средние значения;
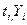 - текущие
значения;
- текущие
значения;
n -
число уровней ряда.
Построим линейную модель регрессии 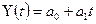 .
.
Получим параметры линейной модели регрессии
с помощью инструмента Регрессии Пакета анализа данных в MS Excel.
Для этого:
·
в главном меню выбираем Сервис/Анализ данных/ Регрессия (рис. 6). Щелкаем по кнопке ОК.
·
заполняем формы в диалоговом окне Регрессия (рис.7): входной интервал Y - $C$3$C$11, входной интервал Х - $В$3$В$11; параметры вывода – Новый рабочий лист; в поле Остатки
ставим необходимые флажки. Щелкаем по кнопке ОК.
Рис.6. Анализ
данных.
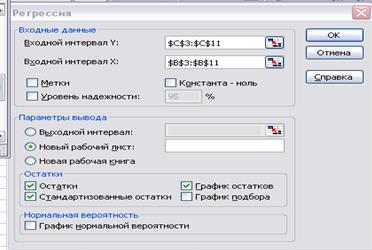
Рис.7.
Регрессия
Получаем результаты расчета Регрессии
(таблица5).
Таблица 5
|
Регрессионная статистика
|
|
|
Множественный
R
|
0,976677712
|
|
|
R-квадрат
|
0,953899353
|
|
|
Нормированный
R-квадрат
|
0,947313546
|
|
|
Стандартная
ошибка
|
1,576866493
|
|
|
Наблюдения
|
9
|
|
|
Дисперсионный
анализ
|
|
|
F-табличное:
|
5,591447848
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
|
Регрессия
|
1
|
360,15
|
360,15
|
144,8416853
|
6,23516E-06
|
|
|
Остаток
|
7
|
17,40555556
|
2,486507937
|
|
|
|
|
Итого
|
8
|
377,5555556
|
|
|
|
|
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
|
|
Y-пересечение
|
46,97222222
|
1,145566948
|
41,00347194
|
1,33788E-09
|
44,26338684
|
49,68105761
|
44,26338684
|
49,68105761
|
|
t
|
2,45
|
0,203572589
|
12,03501912
|
6,23516E-06
|
1,96862732
|
2,93137268
|
1,96862732
|
2,93137268
|
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
|
|
49,68105761
|
44,26338684
|
49,68105761
|
|
|
2,93137268
|
1,96862732
|
2,93137268
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вывод: полученная модель
имеет вид 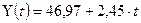
3.
Оценка адекватности уравнения модели.
Модель считается хорошей со статистической
точки зрения, если она адекватна и достаточно
точна. Под адекватностью понимается соответствие модели исследуемому
процессу, т.е. наблюдается соответствие значений определенных по кривой роста, 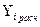 фактическим данным
фактическим данным 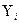 .
.
Модель является адекватной, если значения остаточной
последовательности 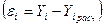 удовлетворяют ряду
требований:
удовлетворяют ряду
требований:
·
значения остаточной последовательности 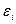 должны быть
случайными величинами;
должны быть
случайными величинами;
·
значения остаточной последовательности должны
быть независимыми случайными величинами,
т.е. не должно наблюдаться автокорреляции в остаточной последовательности.
·
значение 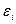 должны быть
распределены по нормальному закону;
должны быть
распределены по нормальному закону;
·
Математическое ожидание значений остаточной
последовательности должно быть близким к нулю.
а) оценка случайности остаточной компоненты
по критерию пиков.
Для оценки случайности остаточной компоненты
построенной модели исследуем ряд остатков отклонений расчетных значений 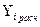 от фактических
от фактических 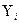 . Для этого проведем предварительные расчеты, результаты
которых приведены в таблице 6.
. Для этого проведем предварительные расчеты, результаты
которых приведены в таблице 6.
Таблица 6
Расчет остатков регрессионной модели
|
№
|
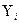
|
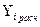
|
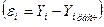
|
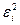
|
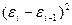
|
Число пиков
|
|
1
|
50
|
49,42222222
|
0,577777778
|
0,33382716
|
-
|
-
|
|
2
|
52
|
51,87222222
|
0,127777778
|
0,01632716
|
0,2025
|
0
|
|
3
|
54
|
54,32222222
|
-0,322222222
|
0,10382716
|
0,2025
|
1
|
|
4
|
59
|
56,77222222
|
2,227777778
|
4,962993827
|
6,5025
|
1
|
|
5
|
57
|
59,22222222
|
-2,222222222
|
4,938271605
|
19,8025
|
1
|
|
6
|
60
|
61,67222222
|
-1,672222222
|
2,79632716
|
0,3025
|
0
|
|
7
|
63
|
64,12222222
|
-1,122222222
|
1,259382716
|
0,3025
|
0
|
|
8
|
68
|
66,57222222
|
1,427777778
|
2,038549383
|
6,5025
|
1
|
|
9
|
70
|
69,02222222
|
0,977777778
|
0,956049383
|
0,2025
|
-
|
|
Итого
|
|
2,227777778
|
17,40555556
|
34,02
|
4
|
Определим количество поворотных точек, т.е.
таких точек, значение уровня в которых одновременно больше соседних с ним или
наоборот, одновременно меньше предыдущего и последующего за ним уровня.
Введем обозначения: 1 – точка поворота; 0 –
отсутствие точки поворота.
Из
расчета (таблица 6) и графика остатков (рис.8) видно, что количество поворотных
точек р=4.
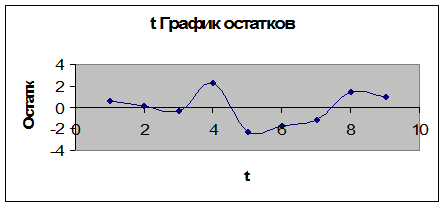
Рис. 8. График остатков.
Критическое
число поворотных точек определяется по формуле:
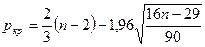 ,
,
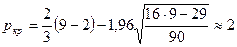
Вывод:
т.к. фактическое значение поворотных точек р=4 больше, чем критическое
значение ркрит=2, то значения остаточной
последовательности можно считать случайными величинами. Модель по критерию случайности адекватна.
б) оценка независимости уровней ряда
остатков по d-критерию.
Процедура представляет проверку отсутствия
автокорреляции в остаточной последовательности и осуществляется по d-критерию Дарбина-Уотсона:
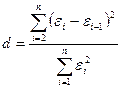 ,
,
По данным таблицы 6:
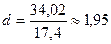
Вывод:
т.к. D>1,08 то можно
считать, что модель по данному критерию адекватна.
в) оценка нормальности распределения
остаточной компоненты по R/S-критерию.
Метод проверки нормальности распределения
остаточной компоненты основан на R/S-критерии.
Значение этого критерия численно равно отношению размаха случайной величины R к стандартному отклонению 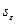 :
:
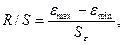
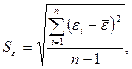
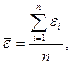
где
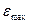 и
и 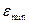 -максимальный и
минимальный уровни ряда остатков;
-максимальный и
минимальный уровни ряда остатков;
 - среднеквадратическое отклонение;
- среднеквадратическое отклонение;
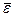 - среднее значение
ряда остатков;
- среднее значение
ряда остатков;
n - количество уровней ряда.
Берем
значения из таблицы 6: 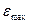 =2,23 ,
=2,23 , 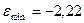
Тогда
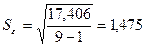
Найдем
R=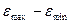 =2,23-(-2,22)=4,45
=2,23-(-2,22)=4,45
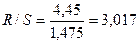
Так как R/S=3,017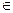 [2,7 - 3,7], то модель адекватна по R/S-критерию.
[2,7 - 3,7], то модель адекватна по R/S-критерию.
Общие выводы:
- линейная трендовая модель является адекватной
фактическому ряду динамики;
- модель может быть использована для построения
прогнозных оценок.
4. Оценка точности модели.
Точность модели
характеризуется величиной отклонения фактического уровня временного ряда и его
оценкой, полученной расчетным путем, с использованием трендовой модели.
В качестве статистических
показателей точности применяются среднеквадратическое отклонение и средняя
относительная по модулю ошибка аппроксимации.
Среднеквадратическое отклонение определяется по
формуле:
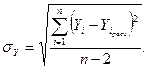
Так как 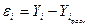 , то из таблицы 6 видно, что
, то из таблицы 6 видно, что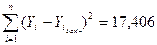 .
.
Тогда 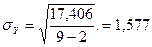 .
.
Средняя относительная по
модулю ошибка аппроксимации определяется по формуле 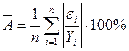 . Получаем
. Получаем 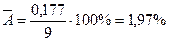 . Таким образом
. Таким образом 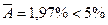 .
.
Вывод: модель имеет достаточную
точность и может быть использована для оценочных расчетов прогноза.
5. Точечный и
интервальный прогнозы
Для периода упреждения на 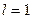 шаг вперед
шаг вперед
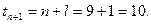
Для
периода упреждения на 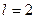 шага вперед
шага вперед
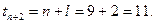
Подставив
найденные значения 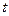 в линейную модель
в линейную модель 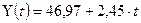 , получим точечные прогнозные значения:
, получим точечные прогнозные значения:
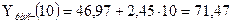
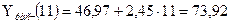 .
.
Интервальный
прогноз рассчитывается по формуле:
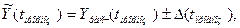
где
доверительный интервал
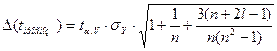 .
.
Тогда
при табличном значении критерия Стьюдента 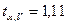
для
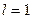
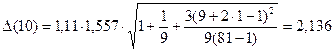
для
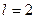
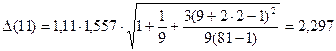 .
.
Интервальный
прогноз на два шага вперед при уровне вероятности P = 70%
 ,
, 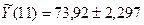
Результаты
прогнозных оценок по модели представлены в таблице 7.
Таблица 7
Прогнозные
оценки по уравнению регрессии
|
|
|
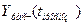
|
Нижняя граница
|
Верхняя граница
|
|
10
|
1
|
71,47
|
69,584
|
73,606
|
|
11
|
2
|
73,92
|
71,623
|
76,217
|
Результаты прогнозирования с помощью
инструмента Регрессии Пакета анализа данных в MS Excel представлены в табл.8 и на рис.9
Таблица 8
|
5.
Построить точечный интервальный прогноз на два шага вперед.
|
|
|
|
|
|
|
|
|
Время
t
|
Шаг
k
|
Прогнозы
Yp(t)
|
Нижняя
граница
|
Верхняя
граница
|
|
10
|
1
|
71,47222222
|
69,72190042
|
73,22254403
|
|
11
|
2
|
73,92222222
|
72,17190042
|
75,67254403
|
|
дельта:
|
1,750321807
|
|
|
|
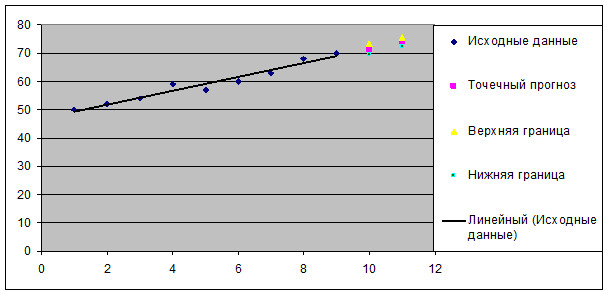
Рис.9. Прогнозирование по линейной модели
Задание II
Таблица 9
|
Исходные
данные:
|
|
|
|
|
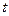
|
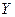
|
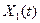
|
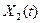
|
|
1
|
50
|
25
|
75
|
|
2
|
52
|
27
|
77
|
|
3
|
54
|
30
|
73
|
|
4
|
59
|
31
|
70
|
|
5
|
57
|
35
|
66
|
|
6
|
60
|
41
|
63
|
|
7
|
63
|
42
|
67
|
|
8
|
68
|
45
|
63
|
|
9
|
70
|
47
|
61
|
1.
Построить матрицу коэффициентов парной корреляции 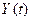 с
с 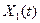 и
и 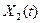 , выбрать фактор,
, выбрать фактор, наиболее тесно
связанный с зависимой переменной
наиболее тесно
связанный с зависимой переменной 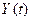 ;
;
2.
Построить линейную однопараметрическую модель регрессии
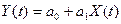 ;
;
3.
Оценить качество построенной модели, исследовав ее
адекватность и точность;
4.
Для модели регрессии рассчитать коэффициент
эластичности и 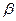 -коэффициент;
-коэффициент;
5.
Построить точечный и интервальный прогнозы на два шага
вперед по модели регрессии (для вероятности Р=70% использовать коэффициент  ). Прогнозные оценки фактора
). Прогнозные оценки фактора 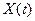 на два шага вперед получить
на основе среднего прироста от фактически достигнутого уровня.
на два шага вперед получить
на основе среднего прироста от фактически достигнутого уровня.
Решение.
1. Матрица коэффициентов
парной корреляции 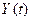 с
с 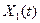 и
и 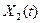
На
основании анализа матрицу коэффициентов парной корреляции определяют взаимную
зависимость переменных.
Выборочный парный линейный коэффициент корреляции рассчитывается по
формуле:
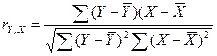 .
.
Промежуточные результаты расчетов для
коэффициентов приведены в таблице 10.
Таблица 10
Рабочая
таблица для вычисления коэффициентов корреляции
|
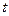
|
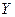
|
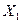
|
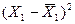
|
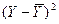
|
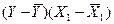
|
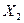
|
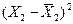
|
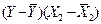
|
|
1
|
50
|
25
|
118,570321
|
85,045284
|
100,418358
|
75
|
44,448889
|
-61,483074
|
|
2
|
52
|
27
|
79,014321
|
52,157284
|
64,196358
|
77
|
75,116889
|
-62,593074
|
|
3
|
54
|
30
|
34,680321
|
27,269284
|
30,752358
|
73
|
21,780889
|
-24,371074
|
|
4
|
59
|
31
|
23,902321
|
27,269284
|
1,085358
|
70
|
2,778889
|
-0,370074
|
|
5
|
57
|
35
|
0,790321
|
4,937284
|
1,975358
|
66
|
5,442889
|
5,183926
|
|
6
|
60
|
41
|
26,122321
|
0,605284
|
3,976358
|
63
|
28,440889
|
-4,149074
|
|
7
|
63
|
42
|
37,344321
|
14,273284
|
23,087358
|
67
|
1,776889
|
-5,036074
|
|
8
|
68
|
45
|
83,010321
|
77,053284
|
79,976358
|
63
|
28,440889
|
-46,813074
|
|
9
|
70
|
47
|
123,454321
|
116,165284
|
119,754358
|
61
|
53,772889
|
-79,035074
|
|
Сумма
|
533
|
323
|
526,8889
|
404,7756
|
425,2222
|
615
|
262
|
-278,667
|
|
Среднее
|
59,222
|
35,889
|
-
|
-
|
-
|
68,333
|
-
|
-
|
|
СКО
|
7,113
|
8,115
|
-
|
-
|
-
|
5,723
|
-
|
-
|
Тогда коэффициенты корреляции

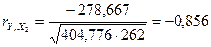
Вычислим
коэффициент 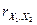 . Составим вспомогательную таблицу:
. Составим вспомогательную таблицу:
Таблица 11
Таблица для вычисления коэффициента корреляции 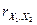
|
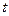
|
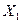
|
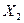
|
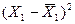
|
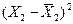
|
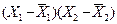
|
|
1
|
25
|
75
|
118,570321
|
44,448889
|
-72,596963
|
|
2
|
27
|
77
|
79,014321
|
75,116889
|
-77,040963
|
|
3
|
30
|
73
|
34,680321
|
21,780889
|
-27,483963
|
|
4
|
31
|
70
|
23,902321
|
2,778889
|
-8,149963
|
|
5
|
35
|
66
|
0,790321
|
5,442889
|
2,074037
|
|
6
|
41
|
63
|
26,122321
|
28,440889
|
-27,256963
|
|
7
|
42
|
67
|
37,344321
|
1,776889
|
-8,145963
|
|
8
|
45
|
63
|
83,010321
|
28,440889
|
-48,588963
|
|
9
|
47
|
61
|
123,454321
|
53,772889
|
-81,476963
|
|
Сумма
|
323
|
615
|
526,8889
|
262
|
-348,667
|
Таким образом 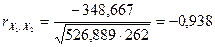
Запишем матрицу коэффициентов парной корреляции:
Таблица 12
матрица
коэффициентов парной корреляции
|
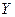
|
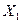
|
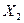
|
|
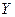
|
1
|
0,921
|
-0,856
|
|
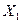
|
0,921
|
1
|
-0,938
|
|
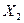
|
-0,856
|
-0,938
|
1
|
Построим
матрицу коэффициентов парной корреляции с помощью Пакета анализа данных в MS Excel. Для этого:
·
В главном меню выбираем Сервис/Анализ данных/Корреляция. Щелкаем
по кнопке OK.
·
Заполняем формы в диалоговом окне Корреляция: входной интервал - $B$3:$D$11, выходной интервал $A$13. Щелкаем по кнопке OK.
Анализ
матрицы парной корреляции показывает, что фактор 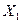 наиболее тесно
связан с зависимой переменной
наиболее тесно
связан с зависимой переменной 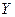 , так как
, так как 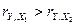 (по модулю) ( 0,921>0,856) , т.е.
(по модулю) ( 0,921>0,856) , т.е. 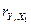 наиболее близок к 1.
наиболее близок к 1.
2. Построение линейной
однопараметрической модели регрессии 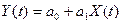
Построим
линейной однопараметрической модели регрессии для 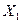 :
:
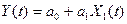
Так
как данная модель линейна относительно параметров 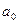 и
и 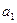 , то для их оценки применим метод наименьших квадратов. Тогда
, то для их оценки применим метод наименьших квадратов. Тогда
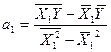 ,
, 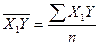 ,
, 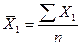 ,
, 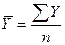 ,
, 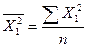 ,
, 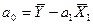 ,
,
где
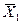 ,
, 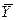 ,
, 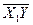 ,
, 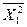 - средние значения;
- средние значения;
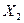 ,
, 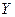 - текущие значения;
- текущие значения;
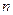 - число уровней ряда.
- число уровней ряда.
Результаты
предварительных расчетов приведены в таблице 13.
Таблица 13
Рабочая
таблица для расчета параметров регрессии.
|
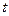
|
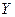
|
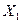
|
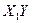
|
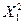
|
|
1
|
50
|
25
|
1250
|
625
|
|
2
|
52
|
27
|
1404
|
729
|
|
3
|
54
|
30
|
1620
|
900
|
|
4
|
59
|
31
|
1829
|
961
|
|
5
|
57
|
35
|
1995
|
1225
|
|
6
|
60
|
41
|
2460
|
1681
|
|
7
|
63
|
42
|
2646
|
1764
|
|
8
|
68
|
45
|
3060
|
2025
|
|
9
|
70
|
47
|
3290
|
2209
|
|
Сумма
|
533
|
323
|
19554
|
12119
|
|
Среднее
|
59,222
|
35,889
|
2172,667
|
1346,556
|
Определим
коэффициент регрессии 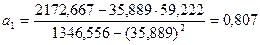
Определим
значение постоянной величины 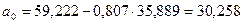
Уравнение
регрессии имеет вид: 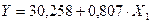 .
.
Получим параметры линейной
модели парной регрессии с помощью Пакета Регрессия
в MS Excel. Для этого:
·
В главном меню выбираем Сервис/Анализ данных/ Регрессия. Щелкаем по кнопке OK
(рис.10).
Рис.10 Анализ данных
·
Заполняем формы в диалоговом окне Регрессия: входной интервал 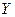 - $B$3:$B$11,
- $B$3:$B$11, 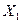 - $C$3:$C$11
выходной интервал $A$63; в поле Остатки ставим
необходимые флажки. Щелкаем по кнопке OK
(рис.11).
- $C$3:$C$11
выходной интервал $A$63; в поле Остатки ставим
необходимые флажки. Щелкаем по кнопке OK
(рис.11).
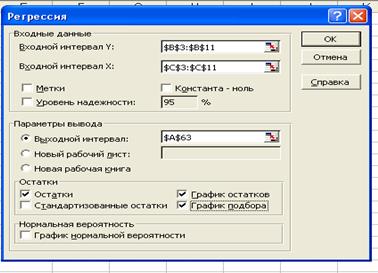
Рис. 11 Регрессия
Получаем
результата расчета Регрессия (таблица 14).
Таблица 14
Параметры
регрессии, полученные в Excel
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
|
Y-пересечение
|
30,25832982
|
3,543022432
|
8,540259172
|
|
X1
|
0,807043442
|
0,096552109
|
8,35863091
|
Во втором столбце табл.14
содержатся коэффициенты уравнения регрессии 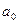 и
и 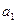 . В третьем столбце содержатся стандартные ошибки
коэффициентов уравнения регрессии, в четвертом столбце – t
–статистика, используемая для проверки значимости коэффициентов уравнения
регрессии.
. В третьем столбце содержатся стандартные ошибки
коэффициентов уравнения регрессии, в четвертом столбце – t
–статистика, используемая для проверки значимости коэффициентов уравнения
регрессии.
Уравнение регрессии имеет
вид:
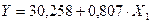
3. Оценка адекватности и
точности линейной
однопараметрической
модели регрессии
Для оценки адекватности и
точности линейной однофакторной модели регрессии необходимо убедиться в
следующем:
·
в адекватности вида уравнения модели;
·
в статистической значимости модели регрессии в
целом (F – критерий
Фишера);
·
в статистической значимости коэффициентов
уравнения регрессии и коэффициента корреляции;
·
в точности модели (в качестве меры точности
используются оценки значения ошибок).
3.1. Оценка
адекватности уравнения модели
Уравнение
модели является адекватным, если:
а) математическое ожидание
значений остаточного ряда равно или
близко
нулю (t – критерий Стьюдента);
б)
значения остаточного ряда 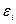 случайны (критерий
пиков);
случайны (критерий
пиков);
в)
значения остаточного ряда независимы (d – критерий Дарбина-Уотсона);
г) значение 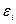 распределены по нормальному закону (R/S – критерий).
распределены по нормальному закону (R/S – критерий).
а) t – критерий Стьюдента
Проверка
равенства математического ожидания уровней ряда остатков нулю осуществляется в
ходе проверки статистической гипотезы 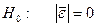 . С этой целью находим t – критерий Стьюдента:
. С этой целью находим t – критерий Стьюдента:
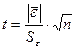
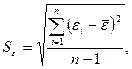
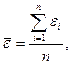
где 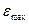 и
и 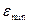 -максимальный и
минимальный уровни ряда остатков;
-максимальный и
минимальный уровни ряда остатков;
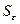 - среднеквадратическое отклонение;
- среднеквадратическое отклонение;
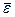 - среднее значение
ряда остатков;
- среднее значение
ряда остатков;
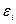 - текущие значения
уровней ряда остатков;
- текущие значения
уровней ряда остатков;
n - количество уровней ряда.
Промежуточные
результаты расчетов, выполненных для t–критерий Стьюдента, а также для остальных критериев адекватности,
приведены в таблице 15.
Среднеквадратическое
отклонение: 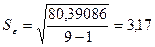
t – критерий
Стьюдента: 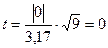
Так
как расчетное значение t – критерия Стьюдента меньше
табличного значения 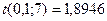 , то гипотеза о равенстве нулю математического ожидания
значений остаточного ряда выполняется. Модель
адекватна по t-критерию
Стьюдента.
, то гипотеза о равенстве нулю математического ожидания
значений остаточного ряда выполняется. Модель
адекватна по t-критерию
Стьюдента.
б) Оценка
случайности остаточной компоненты по критерию пиков
Из расчетов (табл.15) и
графика остатков (рис.12) видно, что количество поворотных точек p = 4.
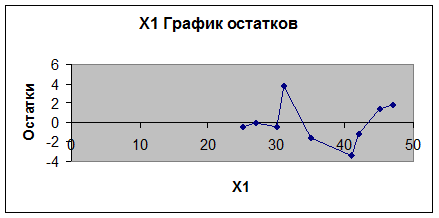
Рис. 12.
График остатков
Таблица
15
Промежуточные
расчеты для статистических критериев
|
|
|
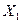
|
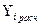
|
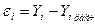
|
Точка
поворота
|
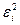
|
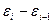
|
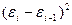
|
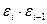
|
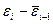
|
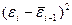
|
|
1
|
50
|
25
|
50,43441586
|
-0,434415858
|
-
|
0,189
|
-
|
-
|
-
|
-0,434
|
0,189
|
|
2
|
52
|
27
|
52,04850274
|
-0,048502741
|
1
|
0,002
|
0,386
|
0,148996
|
0,021
|
-0,049
|
0,002
|
|
3
|
54
|
30
|
54,46963307
|
-0,469633066
|
1
|
0,221
|
-0,421
|
0,177241
|
0,023
|
-0,470
|
0,221
|
|
4
|
59
|
31
|
55,27667651
|
3,723323492
|
1
|
13,863
|
4,193
|
17,581249
|
-1,749
|
3,723
|
13,863
|
|
5
|
57
|
35
|
58,50485027
|
-1,504850274
|
0
|
2,265
|
-5,228
|
27,331984
|
-5,603
|
-1,505
|
2,265
|
|
6
|
60
|
41
|
63,34711092
|
-3,347110924
|
1
|
11,203
|
4,852
|
23,541904
|
-5,036
|
-3,347
|
11,203
|
|
7
|
63
|
42
|
64,15415437
|
-1,154154365
|
0
|
1,332
|
2,193
|
4,809249
|
3,863
|
-1,154
|
1,332
|
|
8
|
68
|
45
|
66,57528469
|
1,42471531
|
0
|
2,03
|
2,579
|
6,651241
|
-1,644
|
1,425
|
2,03
|
|
9
|
70
|
47
|
68,18937157
|
1,810628427
|
-
|
3,278
|
0,386
|
0,148996
|
2,58
|
1,811
|
3,278
|
|
Сумма
|
533
|
323
|
|
0
|
4
|
34,383
|
|
80,39086
|
-7,545
|
|
34,383
|
|
Среднее
|
59,222
|
35,889
|
|
0
|
|
|
|
|
|
|
|
Критическое
число поворотных точек определяется по формуле:
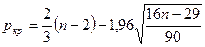 ,
,
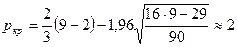
Так как фактическое значение поворотных
точек р=4 больше, чем критическое значение
 , то значения остаточной компоненты можно считать случайными
величинами. Модель по критерию
случайности адекватна.
, то значения остаточной компоненты можно считать случайными
величинами. Модель по критерию
случайности адекватна.
б) Оценка независимости уровней ряда
остатков по d-критерию.
Процедура представляет проверку отсутствия
автокорреляции в остаточной последовательности и осуществляется по d-критерию Дарбина-Уотсона:
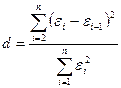 ,
,
По данным таблицы 15:
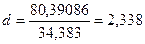
Т.к. 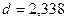 не попадает в промежуток
не попадает в промежуток 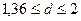 , то можно считать, что в остаточной последовательности наблюдается автокорреляции и значения
, то можно считать, что в остаточной последовательности наблюдается автокорреляции и значения 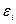 являются зависимыми
случайными величинами. Модель не адекватна
по d- критерию Дарбина-Уотсона.
являются зависимыми
случайными величинами. Модель не адекватна
по d- критерию Дарбина-Уотсона.
г) Оценка нормальности распределения
остаточной компоненты по R/S-критерию.
Метод проверки нормальности распределения
остаточной компоненты основан на R/S-критерии.
Значение этого критерия численно равно отношению размаха случайной величины R к стандартному отклонению 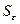 :
:
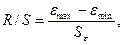
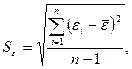
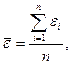
где
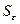 - среднеквадратическое отклонение;
- среднеквадратическое отклонение;
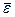 - среднее значение
ряда остатков;
- среднее значение
ряда остатков;
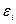 - текущие значения
уровней ряда остатков;
- текущие значения
уровней ряда остатков;
n - количество уровней ряда.
Берем
значения из таблицы 15:
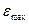 =3,723 ,
=3,723 , 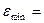 -3,347,
-3,347, 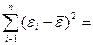 80,391
80,391
Тогда 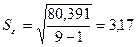 R=
R= =7,07
=7,07
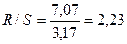
Так как R/S=2,23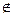 [2,7 - 3,7], то модель не адекватна по R/S-критерию.
[2,7 - 3,7], то модель не адекватна по R/S-критерию.
3.2. Статистическая значимость модели регрессии в целом
(F – критерий Фишера)
F – критерий Фишера
применяется для установления истинности статистической гипотезы о том, что
фактор регрессии 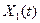 действительно влияет
на зависимую переменную
действительно влияет
на зависимую переменную 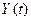 или, точнее,
действительно ли часть дисперсии переменной
или, точнее,
действительно ли часть дисперсии переменной 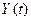 объясняется влиянием
объясняется влиянием 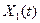 .
.
F – критерий Фишера
рассчитывается по формуле:
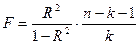 ,
,
где 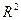 - коэффициент
детерминации;
- коэффициент
детерминации;
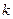 - число параметров при переменных, включенных в
модель;
- число параметров при переменных, включенных в
модель;
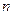 - количество уровней ряда.
- количество уровней ряда.
Используя введенные ранее обозначения, коэффициент
детерминации можно записать в виде:
Для
однофакторной модели значение R
совпадает с 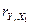 , определенным в пером пункте задания. Тогда, подставив
значения
, определенным в пером пункте задания. Тогда, подставив
значения 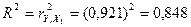 , k = 1 (для линейной однофакторной модели) и n = 9, получим:
, k = 1 (для линейной однофакторной модели) и n = 9, получим:
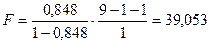
Табличное
значение F – критерия
при  , степенях свободы
, степенях свободы 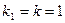 и
и 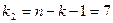 согласно [2, стр. 111]:
согласно [2, стр. 111]: 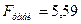 .
.
Так как расчетное значение 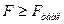 ( 39,053 > 5,59), то модель считается статистически
значимой. Коэффициент детерминации
( 39,053 > 5,59), то модель считается статистически
значимой. Коэффициент детерминации 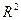 показывает долю
вариации результативного признака под воздействием изучаемого фактора. В задаче
показывает долю
вариации результативного признака под воздействием изучаемого фактора. В задаче
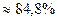 вариации зависимой
переменной
вариации зависимой
переменной 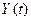 учтено в модели и
обусловлено влиянием включенного фактора
учтено в модели и
обусловлено влиянием включенного фактора 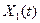 .
.
3.3. Статистическая значимость коэффициентов регрессии и корреляции
Оценка
значимости коэффициентов регрессии и корреляции проводится с помощью t – критерия Стьюдента путем сопоставления значений
коэффициентов с величиной случайной ошибки 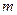 :
:
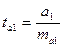 ,
, 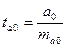 ,
, 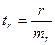 .
.
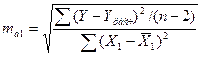 ,
, 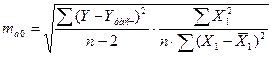 ,
, 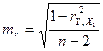 .
.
Промежуточные
результаты вычислений приведены в таблице 16.
Таблица 16
Рабочая таблица для определения ошибок коэффициентов модели
|
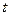
|
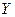
|
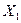
|
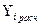
|
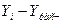
|
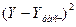
|
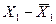
|
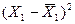
|
|
1
|
50
|
25
|
50,43441586
|
-0,434415858
|
0,189
|
-10,889
|
118,570321
|
|
2
|
52
|
27
|
52,04850274
|
-0,048502741
|
0,002
|
-8,889
|
79,014321
|
|
3
|
54
|
30
|
54,46963307
|
-0,469633066
|
0,221
|
-5,889
|
34,680321
|
|
4
|
59
|
31
|
55,27667651
|
3,723323492
|
13,863
|
-4,889
|
23,902321
|
|
5
|
57
|
35
|
58,50485027
|
-1,504850274
|
2,265
|
-0,889
|
0,790321
|
|
6
|
60
|
41
|
63,34711092
|
-3,347110924
|
11,203
|
5,111
|
26,122321
|
|
7
|
63
|
42
|
64,15415437
|
-1,154154365
|
1,332
|
6,111
|
37,344321
|
|
8
|
68
|
45
|
66,57528469
|
1,42471531
|
2,03
|
9,111
|
83,010321
|
|
9
|
70
|
47
|
68,18937157
|
1,810628427
|
3,278
|
11,111
|
123,454321
|
|
Сумма
|
533
|
323
|
-
|
-
|
34,383
|
-
|
526,8889
|
|
Среднее
|
59,222
|
35,889
|
-
|
-
|
-
|
-
|
-
|
Используя данные табл.16 и 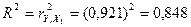 при
при 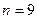 получаем:
получаем:

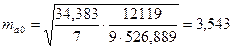
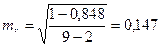
Значения t –статистик (по модулю):
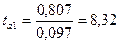 ,
, 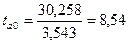 ,
, 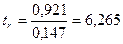 .
.
Табличное значение t –
критерия Стьюдента при  и числе степеней
свободы
и числе степеней
свободы 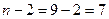 составляет 2,3646. Так
как все фактические значения t –статистик превышают
табличное значение, то коэффициенты
регрессии и корреляции статистически значимы.
составляет 2,3646. Так
как все фактические значения t –статистик превышают
табличное значение, то коэффициенты
регрессии и корреляции статистически значимы.
3.4. Оценка точности модели
В
качестве меры точности модели регрессии применяют несмещенную оценку дисперсии
остаточной компоненты, т.е. части дисперсии фактического явления,
«необъясненную» включенными в модель факторами.
Стандартная
ошибка оценки определяется по формуле:
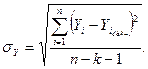
где
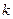 - число факторов, включенных в модель (данном
случае
- число факторов, включенных в модель (данном
случае 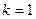 );
);
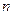 - количество уровней ряда.
- количество уровней ряда.
Из таблицы 16 видно, что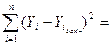 34,383
34,383
Тогда 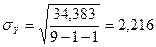 .
.
Средняя относительная ошибка
аппроксимации (по модулю) определяется по формуле  .
.
Промежуточные
расчетные данные приведены в таблице 17.
Таблица 17
Рабочие
расчеты для оценки точности модели
|
|
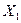
|
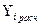
|
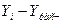
|
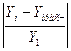
|
|
1
|
50
|
25
|
50,43441586
|
-0,434415858
|
0,009
|
|
2
|
52
|
27
|
52,04850274
|
-0,048502741
|
0,001
|
|
3
|
54
|
30
|
54,46963307
|
-0,469633066
|
0,009
|
|
4
|
59
|
31
|
55,27667651
|
3,723323492
|
0,063
|
|
5
|
57
|
35
|
58,50485027
|
-1,504850274
|
0,026
|
|
6
|
60
|
41
|
63,34711092
|
-3,347110924
|
0,056
|
|
7
|
63
|
42
|
64,15415437
|
-1,154154365
|
0,018
|
|
8
|
68
|
45
|
66,57528469
|
1,42471531
|
0,021
|
|
9
|
70
|
47
|
68,18937157
|
1,810628427
|
0,026
|
|
Сумма
|
-
|
-
|
-
|
-
|
0,229
|
Получаем 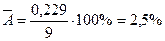 . Таким образом
. Таким образом  .
.
Модель
имеет достаточную точность и может быть использована для оценочных расчетов
прогноза.
4. Коэффициент эластичности и b - коэффициент
Коэффициент эластичности
(т.е. коэффициент, показывающий на сколько процентов изменится результат, если
фактор изменится на 1%) в общем виде определяется как
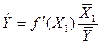 ,
,
где 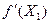 - первая производная функции
- первая производная функции 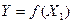 .
.
Так
как для линейной функции коэффициент эластичности зависит от значения фактора 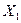 , то воспользуемся формулой среднего коэффициента
эластичности:
, то воспользуемся формулой среднего коэффициента
эластичности:
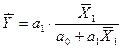
Подставив вычисленные ранее
значения, получим:
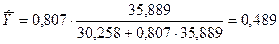 .
.
Стандартизированный b-коэффициент
линейной регрессии определяется из общего уравнения множественной
регрессии в стандартизированном масштабе:
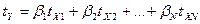 ,
,
где 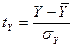 ,
, 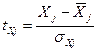 - стандартизированные
переменные;
- стандартизированные
переменные;
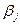 - стандартизированные
коэффициенты регрессии, определяемые из системы уравнений:
- стандартизированные
коэффициенты регрессии, определяемые из системы уравнений:
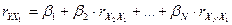
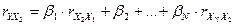
……………………………………..
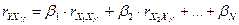
где 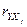 ,
, 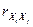 - парные коэффициенты
корреляции.
- парные коэффициенты
корреляции.
Для однопараметрической
(однофакторной) линейной модели система уравнений сводится к тождеству:
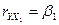 ,
,
откуда
значение b-коэффициента
линейной однофакторной регрессии:
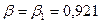
b-коэффициент можно определить также другим способом. По
формуле связи между коэффициентами регрессии в стандартизированной и нормальной
формах имеем:
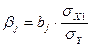 ,
,
где 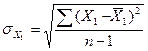 ,
, 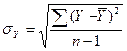 - среднеквадратические
отклонения.
- среднеквадратические
отклонения.
Используя
данные таблицы 10: 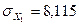 ,
, 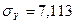 и известный параметр регрессии
и известный параметр регрессии 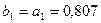 получим:
получим:
Тогда
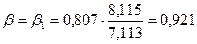
5. Точечный и
интервальный прогнозы
Прогнозируемое точечное значение переменной 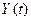 для периода упреждения
на
для периода упреждения
на 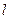 шагов вперед
получается при подстановке в уравнение регрессии ожидаемой величины фактора
шагов вперед
получается при подстановке в уравнение регрессии ожидаемой величины фактора 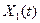 при
при 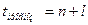 , т.е.
, т.е.
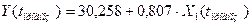
Получим прогнозные оценки фактора 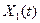 на основе величины его
среднего абсолютного прироста (САП):
на основе величины его
среднего абсолютного прироста (САП):
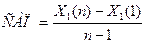 ,
,
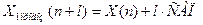 .
.
Подставив соответствующие значения, получим:
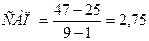
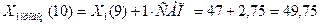
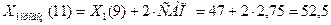
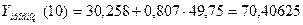
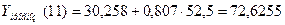
Интервальный
прогноз рассчитывается с помощью доверительного интервала по формуле:
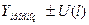 ,
,
где 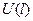 - средняя стандартная
ошибка прогноза:
- средняя стандартная
ошибка прогноза:
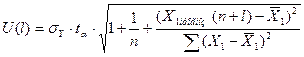 ,
,
где
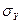 - стандартная ошибка
оценки;
- стандартная ошибка
оценки;
 - табличное
значение критерия Стьюдента для уровня значимости a и для числа
степеней свободы
- табличное
значение критерия Стьюдента для уровня значимости a и для числа
степеней свободы 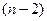 .
.
Подставив известные (по
условию задачи) значения 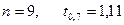 , а также вычисленные ранее значения
, а также вычисленные ранее значения 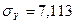 (пункт 3.4),
(пункт 3.4), 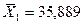 и
и 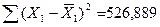 (табл.10), получим:
(табл.10), получим:
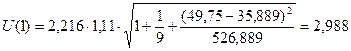
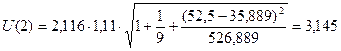
Результаты
прогнозных оценок при уровне вероятности P = 70% по
линейной однопараметрической модели регрессии
представлены в таблице 18.
Таблица 18
Прогнозные
оценки по линейной модели регрессии
|
|
|
|
Нижняя граница
|
Верхняя граница
|
|
10
|
1
|
70,406
|
67,418
|
73,394
|
|
11
|
2
|
72,626
|
69,481
|
75,771
|
Результаты прогнозирования с помощью
инструмента Регрессии Пакета анализа данных в MS Excel представлены на рис.13
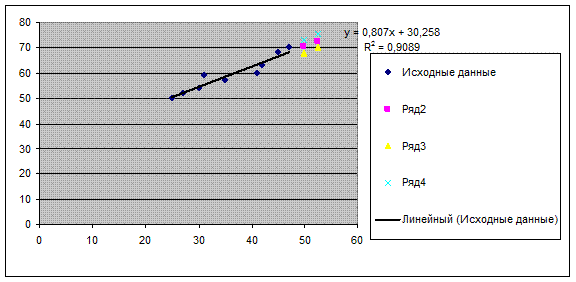 Рис.13. Результаты расчетов и прогнозирования
Рис.13. Результаты расчетов и прогнозирования
Список использованной литературы
1.
Эконометрика. Программа. Методические указания по
изучению дисциплины для студентов 4-го курса второго высшего образования,
обучающихся по специальностям «Финансы и кредит», «Бухгалтерский учет и аудит».
–М.:ЗАО «Финстатинформ», 2001. -68с.
2.
Эконометрика. Методические указания по изучению
дисциплины и выполнению контрольной и аудиторной работы на ПЭВМ для студентов 3 курса, обучающихся по
специальностям «Финансы и кредит», «Бухгалтерский учет, анализ и аудит»,
«Экономика труда». –М.: Вузовский учебник, 2005. -122с.
3.
Эконометрика: Учебник/ Про ред. И.И.Елисеевой. –М.: Финансы и статистика, 2005. –
576с.
4.
Практикум по эконометрике: Учеб.пособие под ред. И.И.Елисеевой.
–М.: Финансы и статистика, 2006. – 192с