Федеральное
агентство по образованию и науке
ГОУ
ВПО
«Новосибирский
Государственный Педагогический Университет»
Курсовая
работа по математике
Тема:
«Задачи с параметрами.
Приложения
к решению других задач»
Руководитель:
Иер А.А.
Новосибирск, 2005
Содержание
Введение. 3
1. Общие положения задач с параметрами. 5
2. Тематическое планирование и содержание
факультатива по теме «Задачи с параметрами. Приложения к решению других задач». 13
2.1. Задачи с параметрами на составление
уравнений и неравенств. 13
2.2. Некоторые задачи с параметрами в анализе. 15
Заключение. 31
Список литературы.. 32
Введение
Есть
много уравнений и неравенств, которые считаются для школьников задачами
повышенной трудности. Такими задачами являются задачи с параметрами. Для их
решения применяются не традиционные методы, а приёмы, которые не совсем
привычны для учащихся.
Актуальность
представленной работы заключается в том, что задачи с параметрами - самый сложный
вопрос математики. При решении задач с параметрами учащимся предстоит применить
все умения и навыки, которые они получили, изучая элементарную математику, в
целом. Считается, что задачи с параметрами обладают в полной мере
диагностической и прогностической ценностью. И не случайно они стали
неотъемлемым атрибутом вступительных экзаменов в вузы и контрольных измерительных
материалов ЕГЭ. Но в школьных учебниках параметрам, по прежнему почти не
уделяется внимания, хотя для достижения хороших результатов знакомство с ними
должно состояться как можно раньше, и предпрофильный курс по выбору для этого
является очень подходящим моментом.
Цели курса решения
параметрических задач заключаются в создании условий и возможности:
оценить обучающимися свой
потенциал с точки зрения образовательной перспективы; уточнить готовность и
способность осваивать математику на повышенном уровне;
получения
обучающимися опыта работы на уровне
повышенных требований, что способствует развитию учебной мотивации;
формирования интереса к
изучению математики через решение задач повышенной сложности;
развития интеллектуальных
умений: логически и аналитически
рассуждать при решении нестандартных задач по математике; находить общее и
учитывать детали;
развития творческих
способностей, умения работать самостоятельно и в группе, вести дискуссию,
аргументировать свою точку зрения и уметь слушать другого[1].
Основная цель
представленной работы - знакомство с различными методами решения задач с
параметрами, основанными на материале программы общеобразовательной школы.
Систематизирован ряд приёмов, приводятся методы решения уравнений и неравенств.
Задачи работы - описать основное содержание задач с
параметрами, проанализировать
тематическое планирование и содержание факультатива по решению задач с
параметрами.
1. Общие
положения задач с параметрами
Изучение и решение задач
с параметрами имеют основной целью следующее:
закрепление навыков и
умений, полученных учащимися на уроках математики (и, при необходимости,
ликвидацию возможных пробелов), для успешного обучения в профильной школе,
расширение представлений
о типах и методах решения математических задач,
выработку умения
классифицировать предложенные задачи по методам их решения,
выработку умения работать с условием задачи, сводя ее к более
простой и узнаваемой, а также быть внимательными и аккуратными с отбором
найденных решений[2].
Рассмотрим
несколько примеров:
1. При
каких значениях параметра a сумма loga (2x
– 1) и loga (2x –
7) равна единице ровно при одном значении x?
Решение. Из
условия задачи следует, что loga (2x
– 1) + loga (2x –
7) = 1 и это уравнение должно иметь только одно решение.
x > log2 7 при a > 0 и a¹1.
Преобразуя
уравнение, получим: (2x – 1)(2x – 7)
= a,
(2x)2
– 8·2x + 7 – a = 0.
Пусть 2x
= y, y > 0; тогда имеем квадратное уравнение y2
– 8y + 7 – a = 0. D = 36 + 4a.
Так как a > 0, то D > 0,
то есть квадратное уравнение имеет два корня. Учитывая условие y > 0,
из двух корней подойти должен только один, то есть y1 >
0, y2£ 0. Таким образом, должно выполняться
условие y1y2=7–a£0, то есть a³7.
Ответ: при aÎ [7; +¥×).
1. При каких значениях параметра a
сумма  не равна
единице ни при каких значениях x?
не равна
единице ни при каких значениях x?
Решение. Составим
сумму и запишем условие: 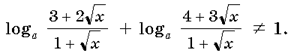
Это условие
равносильно тому, что уравнение 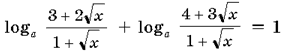 не имеет
решений при любых значениях x.
не имеет
решений при любых значениях x.
x³0 при a > 0 и a¹1.
Преобразуя
наше уравнение, получим равносильное уравнение
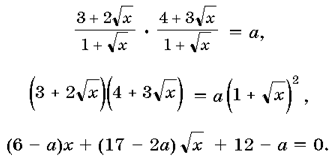
Пусть 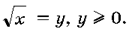 Имеем
квадратное уравнение
Имеем
квадратное уравнение
(6 – a)y2 + (17 – 2a)y + 12 – a = 0 . (1)
D = (17 – 2a2) – 4(6 – a)(12 – a) = 4a + 1.
Так как a
> 0, то D > 0 и квадратное уравнение (1) имеет
два корня. Учитывая условие y³0, имеем y1<0 и
y2<0, то есть y1y2>0, y1+y2<0.
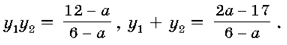
Значит,
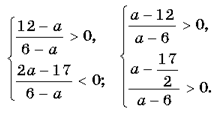
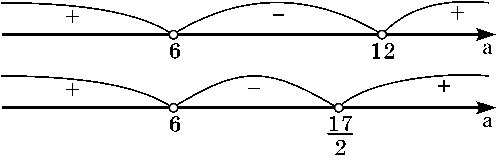
С учетом условия a>0
и a¹1, имеем aÎ(0; 1)È(1; 6)È(12; +¥).
Рассмотрим отдельно случай a=6.
Тогда квадратное уравнение становится линейным: 5y + 6 = 0, то
есть 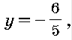 что не удовлетворяет
условию y³0.
что не удовлетворяет
условию y³0.
Ответ: при aÎ(0; 1)È(1; 6]È(12; +¥).
3. При каких значениях параметра
a сумма 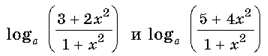 будет
больше единицы при всех значениях x?
будет
больше единицы при всех значениях x?
Решение. 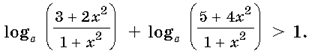
Получили неравенство, которое должно
выполняться при всех значениях x при a>0,
a¹1.
Перепишем неравенство в виде
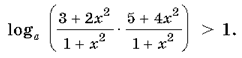
При 0 < a
< 1 имеем 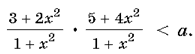 Так как 1+x2>0
при xÎR, то (8–a)x4+(22–2a)x2+(15–a)<0.
Так как 1+x2>0
при xÎR, то (8–a)x4+(22–2a)x2+(15–a)<0.
Пусть x2 = y, y³0. Тогда неравенство (8–a)y2+(22–2a)y+(15–a)<0
должно выполняться при всех yÎ[0;+¥). Это возможно только при 8–a<0,
то есть a>8, что не удовлетворяет условию 0<a<1.
При a>1 имеем 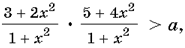 то есть (8–a)x4+(22–2a)x2+(15–a)>0
при всех значениях x.
то есть (8–a)x4+(22–2a)x2+(15–a)>0
при всех значениях x.
Пусть x2 = y, y³0. Тогда (8–a)y2+(22–2a)y+(15–a)>0
должно выполняться при всех yÎ[0; +¥). Это возможно только при 8–a>0.
D=(22–2a)2–4(8–a)(15–a)=4a+4.
При a>1
D>0, то есть квадратный трехчлен имеет два корня y1
и y2 и при yÎ[y1; y2] принимает неположительные значения.
Для того, чтобы квадратный трехчлен был положителен для любого yÎ[0; +¥), необходимо, чтобы y1<0
и y2<0, то есть y1y2>0,
y1+y2<0.
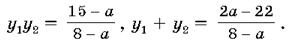
Таким образом, получим систему
неравенств 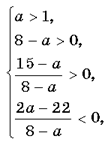 откуда aÎ(1; 8).
откуда aÎ(1; 8).
При a=8
имеем 6y + 7>0 при всех yÎ [0; +¥).
Ответ: при aÎ(1; 8].
4. При каких значениях параметра
a сумма loga (sin x
+ 2) и loga (sin x
+ 3) будет равна единице хотя бы при одном значении x?
Решение. loga (sin x
+ 2) + loga (sin x + 3) =
1. (1)
Получили уравнение, которое должно
иметь хотя бы один корень. a>0, a¹1; xÎR. При этих условиях уравнение (1)
равносильно уравнению
(sin x
+ 2)(sin x + 3) = a,
sin2 x
+ 5sin x + 6 – a =
0.
Пусть sin x
= y, | y | £ 1. Тогда
y2
+ 5y + 6 – a =
0. (2)
D
= 25 – 4(6 – a)
= 4a + 1.
При a > 0
D > 0, то есть уравнение (2) имеет два корня y1
и y2.
Графиком функции f(y) = y2
+ 5y + (6 – a) является парабола,
ветви которой направлены вверх, а абсцисса ее вершины равна –2,5.
Следовательно, меньший корень квадратного уравнения не может принадлежать
отрезку [–1; 1]. Для того, чтобы больший корень принадлежал
отрезку [–1; 1], должны выполняться условия f(–1)£0 и f(1)³ 0, то есть 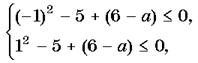 то
есть aÎ[2; 12].
то
есть aÎ[2; 12].
Ответ: при aÎ [2; 12].
5. При каких значениях параметра
a выражение 3 + cos x (a cos x
+ 4sin x) не равно нулю ни при каких значениях x?
Решение. Перефразируем данное
задание: при каких значениях параметра a уравнение
3 + cos x (a cos x + 4sin x) = 0 не имеет решений ни при каких
значениях x?
3sin2 x
+ 4sin x cos x + (a +
3) cos2 x = 0.
Так как cos x = 0
не является решением данного уравнения, то 3tg2 x +
4tg x + (a + 3) = 0. Это
квадратное уравнение не имеет решений только если D < 0, то
есть D = 16 – 12(a + 3) и 16 –
12(a + 3) < 0,
откуда 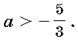
Ответ: при 
6. При каких значениях параметра
a уравнение 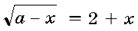 имеет
единственное решение?
имеет
единственное решение?
Решение. 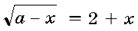 Рассмотрим
условие:
Рассмотрим
условие: 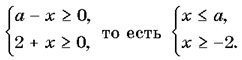
Решим данное уравнение графически.
Рассмотрим графики функций 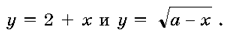 Чтобы исходное
уравнение имело единственное решение, графики наших функций должны иметь только
одну точку пересечения.
Чтобы исходное
уравнение имело единственное решение, графики наших функций должны иметь только
одну точку пересечения.
Графиком функции y = 2 + x
является прямая, проходящая через точки (0; 2) и (2;
4).
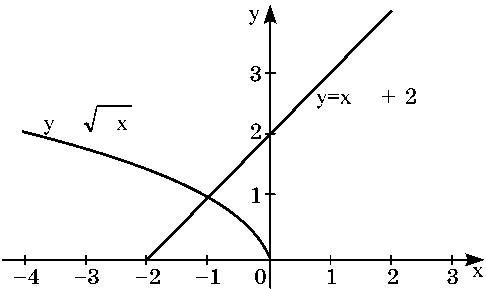
Графиком функции 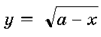 является
кривая, полученная из графика функции
является
кривая, полученная из графика функции 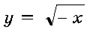 сдвигом
его на | a | единиц
вправо вдоль оси Ox, если a > 0; на | a |
единиц влево вдоль оси Ox, если a<0.
Единственная точка пересечения получается при a³–2.
сдвигом
его на | a | единиц
вправо вдоль оси Ox, если a > 0; на | a |
единиц влево вдоль оси Ox, если a<0.
Единственная точка пересечения получается при a³–2.
Ответ: при aÎ [2; +¥).
7. При каких значениях параметра
a уравнение 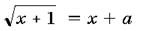 имеет
единственное решение?
имеет
единственное решение?
Решение. 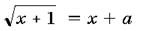 .
Рассмотрим условие:
.
Рассмотрим условие: 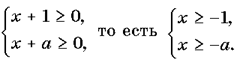
Рассмотрим графики функций 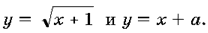 Графиком
функции y = x + a является прямая,
параллельная прямой y = x и проходящая через точку (0;
a).
Графиком
функции y = x + a является прямая,
параллельная прямой y = x и проходящая через точку (0;
a).
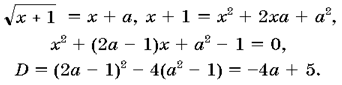
Единственная точка пересечения A при D
= 0, то есть 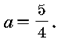
При 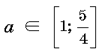 —
две точки пересечения, а при a Î (–¥; 1) — одна точка пересечения.
—
две точки пересечения, а при a Î (–¥; 1) — одна точка пересечения.
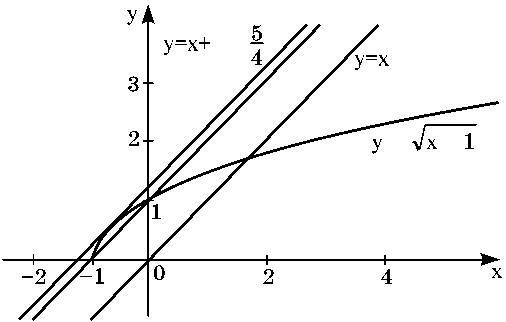
Ответ: при 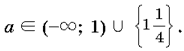
8. При каких значениях параметра
a уравнение 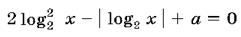 имеет
ровно четыре корня?
имеет
ровно четыре корня?
Решение. 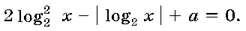 x
> 0.
x
> 0.
Пусть 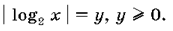 Тогда
уравнение 2y2 – y + a = 0
должно иметь два положительных корня, то есть при D>0 y1>0
и y2>0. Таким образом
Тогда
уравнение 2y2 – y + a = 0
должно иметь два положительных корня, то есть при D>0 y1>0
и y2>0. Таким образом 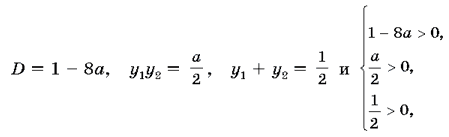
откуда 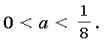 .
.
Ответ: при 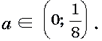
2. Тематическое
планирование и содержание факультатива по теме «Задачи с параметрами.
Приложения к решению других задач»
2.1. ЗАДАЧИ С ПАРАМЕТРАМИ НА СОСТАВЛЕНИЕ УРАВНЕНИЙ И
НЕРАВЕНСТВ
Пример[3]
Из одного
пункта одновременно и в одном направлении выехали два велосипедиста, первый со
скоростью a км/ч, а второй со скоростью b км/ч. Через полчаса в том же
направлении выехал третий велосипедист, который, после того как обогнал первого
велосипедиста, находился в пути ещё полтора часа пока догнал второго.
Определить скорость третьего велосипедиста.
Решение
Заметим
сначала, что из условия задачи видно, что b>a. Далее, пусть v –
скорость третьего велосипедиста, а t – время, за которое он догнал
первого. Тогда имеем систему уравнений
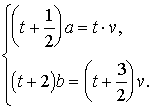
Из первого
уравнения находим t=a/(2(x-a)).
Подставляя
это t во второе уравнение, приходим к уравнению
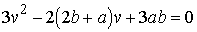 .
Дискриминант этого уравнения всегда положителен, так как при b>a
.
Дискриминант этого уравнения всегда положителен, так как при b>a
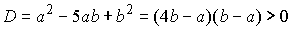 .
.
Следовательно,
само уравнение имеет два вещественных корня
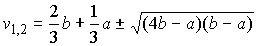 .
.
Однако,
поскольку a<b, то корень уравнения
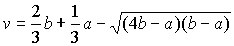
оказывается
меньше b, что противоречит смыслу задачи. Поэтому это значение v не
является решением задачи.
Ответ: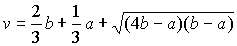 .
.
Пример[4]
Имеется два
раствора йода в спирте. В первом растворе отношение веса йода к весу
растворителя равно p, во втором -q. В каком отношении нужно взять эти растворы,
чтобы получить раствор, в котором отношение веса йода к весу растворителя было
бы равно r?
При каких
соотношениях между p, q, r задача имеет решение?
Решение
Пусть
требуется взять m первого раствора и n г второго раствора.
Если в 1 г первого раствора содержится x г
йода, то растворителя там будет содержатся 1 – x г, значит,
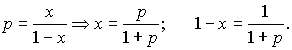
Таким
образом, в m г первого раствора содержится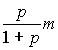 г
йода и
г
йода и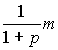 г растворителя.
Аналогично в n г второго раствора содержится
г растворителя.
Аналогично в n г второго раствора содержится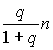 г
йода и
г
йода и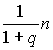 г
растворителя.
г
растворителя.
В задаче
требуется найти отношение 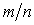 . По
условию имеем
. По
условию имеем
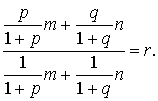
Отсюда
 ;
;
 .
.
Так как  , то
задача имеет решение, когда
, то
задача имеет решение, когда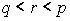 или
или 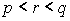 .
.
2.2. НЕКОТОРЫЕ ЗАДАЧИ С
ПАРАМЕТРАМИ В АНАЛИЗЕ
Найти все
значения параметра a, при которых вершины двух парабол 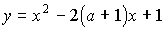 и
и 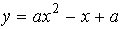 лежат по
разные стороны от прямой y=3/4.
лежат по
разные стороны от прямой y=3/4.
Решение
Найдем
координаты вершин. Ясно, что 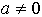
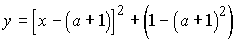 ,
, 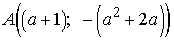
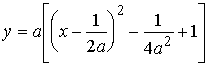 ,
, 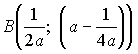 .
.
Вершины лежат
по разные стороны от прямой y=3/4, если a удовлетворяет неравенству
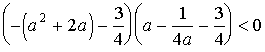 .
.
Отсюда
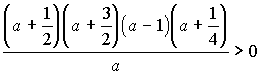 .
.
Ответ:
Следовательно,
условиям задачи удовлетворяют такие a: a>1; --1/4<a<0;
-3/2<a<-1/2.
Пример
Решить
уравнение
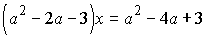 .
.
Решение
Здесь
контрольными будут те значения параметра, при которых коэффициент при x
обращается в ноль, т.е. решения квадратного уравнения 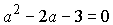 , a=-1,
a=3. При этих значениях a невозможно деление обеих частей уравнения на
коэффициент при x. Если же
, a=-1,
a=3. При этих значениях a невозможно деление обеих частей уравнения на
коэффициент при x. Если же 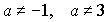 , то
деление возможно. Таким образом, уравнение (1) целесообразно решить отдельно
при:
, то
деление возможно. Таким образом, уравнение (1) целесообразно решить отдельно
при:
1) a=-1; 2)
a=3; 3) 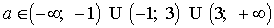 .
.
Рассмотрим
эти случаи.
1) При a=-1
уравнение (1) принимает вид 0x=8. Это уравнение не имеет корней.
2) При a=3
уравнение (1) принимает вид 0x=0. Решением уравнения будет любое число.
3) При 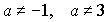 получаем
получаем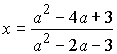 ;
; 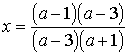 , откуда
x=(a-1)/(a+1).
, откуда
x=(a-1)/(a+1).
Ответ: при
a=-1 корней нет;
при a=3 x – любое;
при 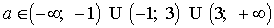 x=(a-1)/(a+1).
x=(a-1)/(a+1).
Пример
Решить
уравнение
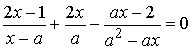 .
.
Решение
При a=0
уравнение (3) теряет смысл и, следовательно, не имеет корней.
При  получим
получим 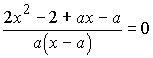 ,
, 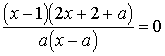 .
.
Корнями
числителя будут 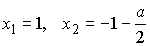 .
.
Исключим из
этих значений те, при которых знаменатель равен нулю.
Если a=1, то
1-a =0 и корнем уравнения будет только x = - 3/2 .
Если
-1-a/2=a, т.е. a=-2/3, то уравнение(3) будет иметь корнем только x=1.
Ответ: 1)
если a=-2/3, то x=1;
2) если a=0, то корней нет;
3) если a=1, то x=-3/2.
Пример
Решить
неравенство
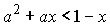 .
.
Решение
Рассматриваемое
неравенство равносильно следующему
 .
.
Контрольным
значением параметра будет a=-1. Нужно рассмотреть следующие случаи: 1) a<-1;
2) a=-1; 3) a>-1.
1) При
a<-1 неравенство равносильно неравенству 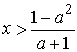 или
x>1-a.
или
x>1-a.
2) При a=-1
получаем 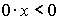 , решений
нет.
, решений
нет.
3) При
a>-1 будем иметь a+1>0, и следовательно, неравенство (4) равносильно
неравенству x<1-a.
Ответ: 1)
если 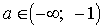 , то
, то 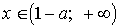 ;
;
2) если a=-1, то решений нет;
3) если 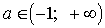 , то
, то 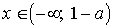 .
.
Пример
Решить
неравенство
 .
.
Решение
При a=1
неравенство (5) теряет смысл и, следовательно, не имеет решений.
При 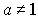 неравенство (5) равносильно неравенству
неравенство (5) равносильно неравенству
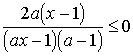 .
.
Контрольным
значением параметра будет a=0. В этом случае неравенство (5) верно при
любом 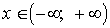 .
.
Если  ,
неравенство (5) равносильно неравенству
,
неравенство (5) равносильно неравенству
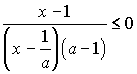 .
Значение a=1 также контрольное.
.
Значение a=1 также контрольное.
1) Рассмотрим
случай a>1. В этом случае a-1>0 и неравенство равносильно
неравенству 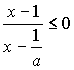 .
.
Так как при a>1, 1/a<1, то решением неравенства будет  .
.
2) В случае
a<1 неравенство равносильно неравенству
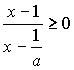 .
.
Если
0<a<1, то 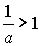 и
решением неравенства будет
и
решением неравенства будет 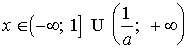 .
.
Если a<0,
то 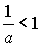 и
решением неравенства (5) будет
и
решением неравенства (5) будет 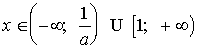 .
.
Ответ: 1)
если 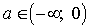 , то
, то 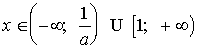 ;
;
2) если a=0, то 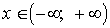 ;
;
3) если 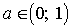 , то
, то 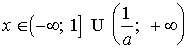 ;
;
4) если a=1, то решений нет;
5) если 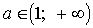 , то
, то  .
.
Пример[5]
Найти все
значения параметра a, для которых неравенство
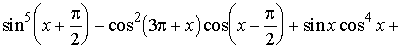
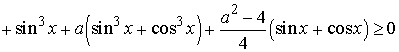
выполнено при
всех x, удовлетворяющих условию 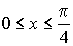 .
.
Решение
Применяя
формулы приведения, получим
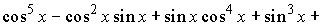
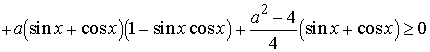 ;
;
 .
.
Так как 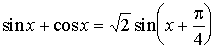 и
при
и
при 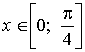 ,
,
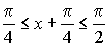 ,
следовательно, sinx+cosx>0.
,
следовательно, sinx+cosx>0.
Так как 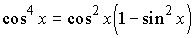 , то
неравенство принимает вид
, то
неравенство принимает вид
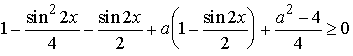 .
.
Пусть
sin2x=t, тогда при 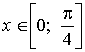 ,
, 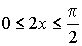 ,
, 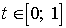 .
.
Таким
образом, задача сводится к нахождению значений a, при которых квадратный
трехчлен 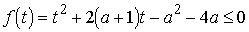 для
всех
для
всех 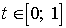 . В силу
утверждения 7 это будет выполняться, если
. В силу
утверждения 7 это будет выполняться, если
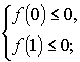

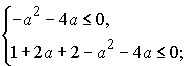

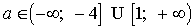 .
.
Ответ: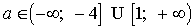 .
.
Пример
Для всех
значений параметра a решить неравенство
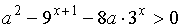 .
.
Решение
После
умножения неравенства на -1 получим
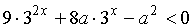 .
.
Обозначим 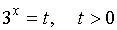 .
.
Корнями
уравнения 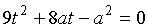 будут
будут
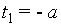 и
и 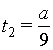 .
.
Тогда при
a>0 решим неравенство (t+a)(t-a/9)<0 методом интервалов
0<t<a/9,
откуда 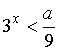 .
.
Прологарифмировав
по основанию, равному 3, получим 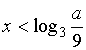 .
.
При a<0
решением неравенства (t+a)(t-a/9)<0 будет интервал (0;-a) 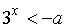 ,
, 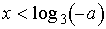 . При a=0
неравенство
. При a=0
неравенство 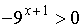 решений не
имеет.
решений не
имеет.
Ответ: при
a<0  ;
;
при a>0 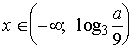 ;
;
при a=0 решений нет.
Пример
Решить
уравнение
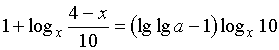 .
.
Решение
Ясно, что
параметр a должен удовлетворять неравенству a>1.
Область
допустимых значений определяется неравенствами
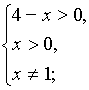

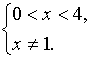
На ОДЗ
исходное уравнение равносильно уравнению
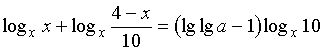 ,
,
откуда 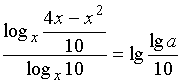 .
.
И после
перехода к десятичному логарифму
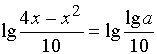
или 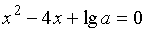 .
Дискриминант последнего уравнения D=4(4-lga), таким образом, при
.
Дискриминант последнего уравнения D=4(4-lga), таким образом, при 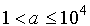
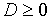 и
уравнение имеет решения
и
уравнение имеет решения
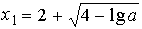 ,
, 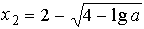 .
.
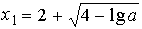 при
всех
при
всех 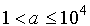 входит в
ОДЗ,
входит в
ОДЗ,
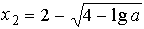 при
при 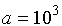 равен 1 и
в ОДЗ не входит.
равен 1 и
в ОДЗ не входит.
Ответ: 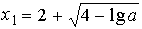 при
при 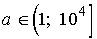 ,
,
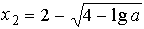 при
при 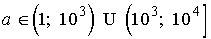 .
.
Пример[6]
Найти все
значения параметра a, при которых неравенство выполняется при всех x
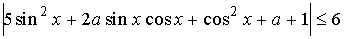 .
.
Решение
При cosx=0
получаем неравенство
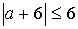 .
.
Его решения
дают ограничения на a:  .
.
При 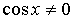 разделим
обе части неравенства на
разделим
обе части неравенства на 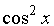 и сделаем
замену t=tgx, получим систему
и сделаем
замену t=tgx, получим систему
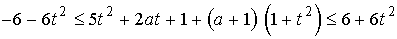
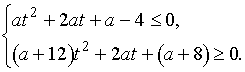
Таким
образом, чтобы исходное неравенство выполнялось при всех x, параметр a должен
удовлетворять системе
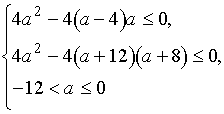

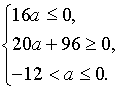

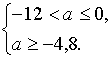
Ответ: 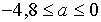 .
.
Пример
Пусть
f(x)=ax2+bx+c имеет действительные корни x1 и x2,
а M – какое-нибудь действительное число, D=b2 -4ас
Утверждение
1. Для того чтобы оба корня квадратного трехчлена были меньше, чем число M
(т.е. лежали на числовой оси левее, чем точка M), необходимо и достаточно
выполнение следующих условий:
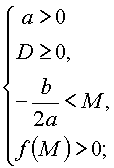 или
или
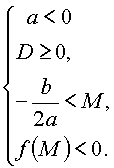

Утверждение 2. Для того чтобы один из корней квадратного трехчлена был
меньше, чем число M, а другой больше, чем число M (т.е. точка M лежала бы между
корнями), необходимо и достаточно выполнение условий:
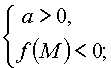
Или
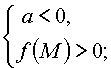
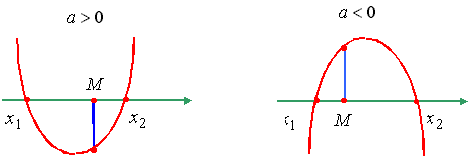
Утверждение 3. Для того чтобы оба корня квадратного трехчлена были
больше, чем число M (т.е. лежали на числовой оси правее, чем точка M),
необходимо и достаточно выполнение условий:
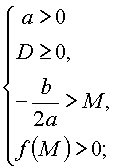
Или
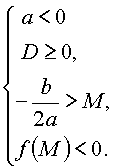
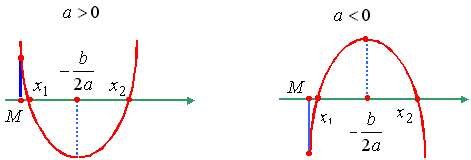
Утверждение 4. Для того чтобы оба корня квадратного трехчлена были
больше, чем число M, но меньше, чем число N (M<N), т.е. лежали в интервале
между M и N, необходимо и достаточно:
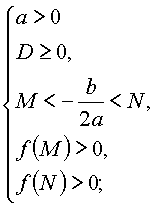
Или
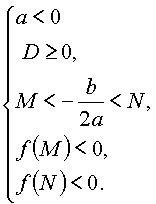
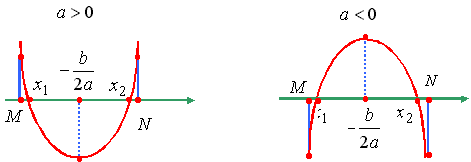
Утверждение 5. Для того чтобы только больший корень квадратного
трехчлена лежал в интервале [M,N] (M < N), необходимо и достаточно:
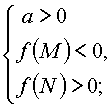
Или
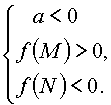 (при этом меньший корень лежит вне отрезка [M, N]).
(при этом меньший корень лежит вне отрезка [M, N]).
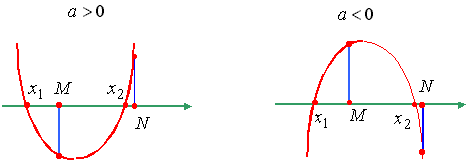
Утверждение 6. Для того чтобы только меньший корень квадратного
трехчлена лежал в интервале [M, N], необходимо и достаточно:
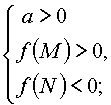
Или
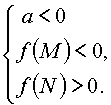
(при этом больший корень
лежит вне отрезка [M, N]).
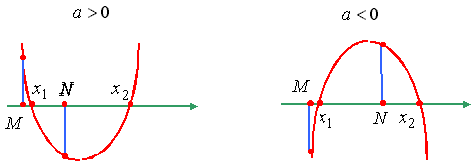
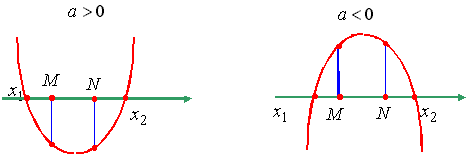
Утверждение 7. Для того чтобы один из корней квадратного трехчлена был
меньше, чем M, а другой больше, чем N (M < N), т.е. отрезок [M, N] целиком
лежал внутри интервала между корнями, необходимо и достаточно:
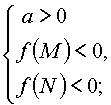
Или
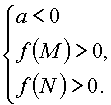
Заключение
В процессе обучения
учащиеся приобретают умения разбираться в типах и методах решения задач по темам,
ставшим популярными в последние годы и на вступительных экзаменах в вузы, и в
контрольных измерительных материалах ЕГЭ (текстовые задачи на проценты, на
составление системы уравнений и неравенств; задачи с параметрами и модулями).
Решение подобного рода
задач открывает перед учащимися значительное число эвристических приемов общего
характера, ценных для математического развития личности, применимых в
исследованиях и на любом другом математическом материале.
Кроме того, с помощью
задач с параметрами обучающемуся на курсе можно проверить свое знание основных
разделов элементарной математики, уровень математического и логического
мышления, первоначальные навыки исследовательской деятельности, а главное,
перспективные возможности успешного овладения курсом математики в профильной
школе и, как следствие, в высшем учебном
заведении[7].
Список
литературы
1.
Алгебра и начала анализа 10-11. Учебник
для средних школ под редакцией А.Н. Колмогорова. – М.: «Просвещение», 1999.
2.
Ангеловски К. Учителя и инновации. М.:
«Наука»,1991.
3.
Батурина Г., Кузина Т. Традиционная
культура воспитания в национальной школе. Педагогика,1995,№2.
4.
Башмаков
М.И. Уравнения и неравенства. М.: Высшая школа, 1971.
5.
Блох
А.Ш., Неверов Г.С. Решение неравенств. Минск, 1962.
6.
Борисенков В.П., Краевский В.В., Кутьев
В.О., Турбовский Я.С. Философия образования. Педагогика,1995, № 4 с.3
7.
Волошинов А. В. Математика и искусство. –
М.: «Народное образование», 1999.
8.
Дорофеев
Г.В., Потопов М.К., Розов Н.Х. Пособие для поступающих в ВУЗы. М.: Высшая
школа, 1970.
9.
Ерина
Т.М. Задачи с параметрами. М.: ЮНИТИ-ДАНА, 2004.
10.
Зильберберг
Н.И. Приобщение к математическому творчеству. Уфа: Башкирское книжное
издательство, 1988.
11.
Газман О.С. Базовая культура и
самоопределение личности. Базовая культура личности: теоретические и методологические
проблемы. Сб.науч. тр. Под ред.Газманова О.С. М., Изд.АПН СССР, 1989,
12.
Груденов Я.И. Совершенствование методики
работы учителя математики. - М.: «Педагогика», 2003.
13.
Ивлев Б.М., Саакян С.М., Шварцбург С.И.
Дидактические материалы по алгебре и началам анализа для 11 класса. – М.:
«Просвещение», 1999.
14.
Карп А.П. Даю уроки математики. – М.:
«Проспект», 1999.
15.
Крылова Н.В. Ребенок в пространстве
культуры. М., «Мысль», 1994.
16.
Культурология. Под ред. Драча Г.В.
Р.-на-Д., Изд. Феникс,1995
17.
Математика. Программа для школы,
работающей по базисному учебному плану. - М., 1999.
18.
Математика. Программа для школ (классов) с
углубленным изучением математики. — М., 1994.
19.
Математика. Программы для
общеобразовательных учреждений. — М.,1994.
20.
Метельский Н.В. Психолого-педагогические
основы дидактики математики. – М.: «Луч», 1997.
21.
Методика преподавания математики в средней
школе. Сборник статей. Составитель Петрова М.И. — М.: Учпедгиз, 1997.
22.
На путях обновления школьного курса
математики. М.: «Педагогика», 2002.
23.
Новиков
Л.С. Элементы математической логики. М.: Просвещение, 1959.
24.
Новые педагогические и
информационные технологии в системе образования // Под ред. Е.С. Полат. – М.,
ACADEMIA, 2001.
25.
Савитская Т.П. Ребенок
в культуре ХХ века. Знание-сила,1995,№4.
26.
Селевко Г.К.
Современные образовательные технологии. – М.: «Народное образование», 2002.
27.
Столяр
А.А. Методы обучения математики. М.: Наука, 1966.
28.
Столяр
А.А. Педагогика математики. М.: Минск, 1969.
29.
Психология. Словарь.
М., 1990.
30.
Учебные стандарты школ
России под ред. В.С Леднева, Н.Д.Никандрова, М.Н. Лазутовой. – М.,
"Прометей", 1998.
31.
Шарыгин И.Ф. Математика для школьников
старших классов. — М.: «Просвещение», 1999.
32.
Щадриков В.Д. Философия образования и
образовательные политики. М., 1993.
33.
Якиманская А.В.
Способности к усвоению математики/ В кн. Развивающее обучение. – М.:
«Просвещение», 2001.
34.
Янченко
М.М. Задачи с параметрами. М.: Издательство «ДРОФА», 2004.
35.
Ястребицкий
Г.А. Уравнения и неравенства, содержащие параметры. М.: Высшая школа, 1972.
[1] Янченко М.М. Задачи с параметрами.
М.: Издательство «ДРОФА», 2004. С. 12.
[2] Ерина Т.М. Задачи с параметрами. М.:
ЮНИТИ-ДАНА, 2004. С. 8.
[3] См.: Ястребицкий Г.А. Уравнения и
неравенства, содержащие параметры. М.: Высшая школа, 1972. С. 142.
[4] См.: Башмаков М.И. Уравнения и
неравенства. М.: Высшая школа, 1971. С. 66.
[5] Дорофеев Г.В., Потопов М.К., Розов
Н.Х. Пособие для поступающих в ВУЗы. М.: Высшая школа, 1970. С. 112.
[6] Блох А.Ш., Неверов Г.С. Решение
неравенств. Минск, 1962. С. 176.
[7] Столяр А.А. Методы обучения математики.
М.: Наука, 1966. С. 33.