Содержание работы:
Задача № 1. 3
Задача № 2. 4
Задача № 3. 5
Задача № 4. 6
Задача № 5. 7
Задача № 6. 8
Задача № 7. 10
Список используемой литературы.. 11
Задача № 1
Рассчитать текущую
стоимость вклада, который через три года составит 15 млн. рублей при начислении
20% в год.
Решение:
Текущая стоимость вклада
рассчитывается по следующей формуле:
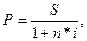где Р – текущая
стоимость вклада, S – будущая стоимость вклада, n – количество лет, i – процентная ставка. Из этой формулы
находим:
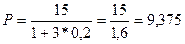млн. рублей.
Ответ: текущая стоимость вклада
составит 9,375 млн. рублей.
Задача № 2
Для
номинальной ставки 20% с начислением процентов раз в квартал найдите
эквивалентную ставку, проценты по которой выплачиваются раз в полгода.
Решение:
Для
решения этой задачи воспользуемся формулой, выраженной из формулы текущей
стоимости. Получается, что
.
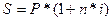При
начислении процентов раз в квартал формула будет выглядеть следующим образом: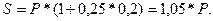 
При
начислении процентов раз в полгода формула будет выглядеть следующим образом: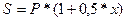 
, где Х – искомая процентная ставка.
Зная,
что текущая стоимость и будущая стоимость равны, составим выражение: 1 + 0,5х =
1,05 => х = 10%
Ответ:
эквивалентная ставка, проценты по которой выплачиваются раз в полгода, равна
10%.
Задача № 3
Сумма
800 денежных единиц инвестируется на три года под 80% годовых. Найти наращенную
сумму и сумму процентов за этот срок. Начисления процентов: А) ежегодные, б)
ежемесячные, в) по полугодиям. Что выгоднее для инвестора?
Решение:
А) S = 800*(1 +
3*0,8) = 2720 д.е.
Сумма процентов = 800*3*0,8 = 1920 д.е.
Б) Ежемесячная процентная ставка составит: (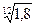
-1)´100% = 3,74%
Тогда S = 800*(1 +
3*12*0,0374) = 1877,12 д.е.
Сумма процентов = 800*3*12 *0,0374 =
1077,12 д.е.
В) Полугодовая процентная ставка составит: (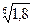
-1)´100% = 7,62%.
Тогда S = 800*(1 +
3*6*0,0762) = 1897,28 д.е.
Сумма процентов = 800*3*6*0,0762 = 1097,28
д.е.
Ответ: из расчетов видно,
что лучше всего для инвестора вложение по первому варианту: он получит большую
сумму денег.
Задача № 4
Два
платежа в 2 и 3 млн. руб. со сроками уплаты соответственно год и три года
объединяются в один платеж со сроком уплаты два года. При консолидации
используется сложная полугодовая ставка равная 10% (начисления по полугодиям).
Определить сумму нового платежа.
Решение:
Будущая
стоимость платежа в 2 млн. со сроком уплаты 1 год составит:
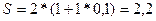млн. руб.
Будущая
стоимость платежа в 3 млн. со сроком уплаты 3 года составит:
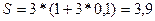млн. руб.
Тогда
общая сумма равна 3,9 + 2,2 = 6,1 млн. руб.
Для
получения этой же суммы, но с учетом консолидации применяется формула сложных
процентов.
Формула
сложных процентов выглядит следующим образом:
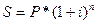. Отсюда выразим Р, потому ее нужно найти.
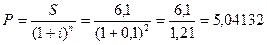млн. руб.
Ответ:
сумма нового платежа составит 5,04132 млн. руб.
Задача № 5
Банк
выдал 300 млн. руб. на год. Требуемая реальная доходность операции 10% годовых.
Ожидаемый годовой уровень инфляции 20%. определить брутто-ставку по кредиту,
погашаемую сумму и сумму полученных процентов.
Решение:
Брутто-ставка
– ставка банковского процента с учетом инфляции, т.е. она равна 10 + 20 = 30%
годовых.
Погашаемая
сумма будет равна:
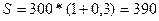тыс. руб.
Сумма
полученных процентов равна 300*0,3 = 90 тыс. руб.
Ответ:
брутто-ставка = 30% годовых, погашаемая сумма = 390 тыс. руб., сумма процентов
за кредит составила = 90 тыс. руб.
Задача № 6
Определить
размеры периодических взносов в фонд размером 100 млн. руб., сформированный за
два года ежемесячными платежами, если процентная ставка 20% годовых. Схема
пренумерандо и постнумерандо. Проценты начисляются: а) раз в год, б) раз в
полгода.
Решение:
А)
Схема пренумерандо
Формула приведенной стоимости
срочного аннуитета
пренумерандо:
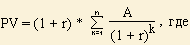
PV - приведенная (текущая) стоимость;
A - величина равномерного поступления; r - процентная ставка; n - количество лет.
Выразим
отсюда А.
100
= (1 + 0,2)*( А/(1 +
0,2)2 + А/(1 + 0,2)1) = 1,2*(0,69А + 0,83А ) = 1,2*1,52А
= 1,824А.
А = 100/1,824 = 54,8 млн.
руб.
Схема
постнумерандо
Формула приведенной стоимости
срочного аннуитета
постнумерандо:
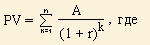
PV - приведенная (текущая) стоимость;
A - величина равномерного поступления; r - процентная ставка; n - количество лет.
Необходимо отсюда выразить А.
100 = А/(1 + 0,2)2 + А/(1
+ 0,2)1 = 0,69А + 0,83А = 1,52А.
А = 100/1,52 = 65,79 млн. руб.
Б)
Схема пренумерандо
100
= (1 + 0,2/2)*( А/(1 +
0,2/2)2 + А/(1 + 0,2/2)1) = 1,1*(0,83А + 0,91А ) = 1,1*1,74А
= 1,914А.
А = 100/1,914 = 52,23
млн. руб.
Схема
постнумерандо
100 = А/(1 + 0,2/2)2 +
А/(1 + 0,2/2)1 = 0,83А + 0,91А = 1,74А.
А = 100/1,74 = 57,5 млн. руб.
Задача № 7
Стороны
согласились пересмотреть условия кредита. Годовые платежи в размере 600
денежных единиц, выплачиваемые в конце года, заменяются ежеквартальными, причем
общий срок кредита остается неизменным. Определить размер разовых
ежеквартальных платежей, если процентная ставка по кредиту равна 10% годовых.
Решение:
Если
взять к примеру срок кредита 1 год, то платеж в конце года равен 600 денежных
единиц. Отсюда можно найти сумму кредита 600*100/10 = 6000 денежных единиц.
При
переходе на ежеквартальные платежи ставка по кредиту равна 10%/4 = 2,5% в
квартал. И тогда 2,5% от суммы 6000 денежных единиц будет равно 150 денежных
единиц.
Ответ:
150 денежных единиц – ежеквартальный платеж.
Список используемой литературы
1.
Bopoнцовский
А. В. Инвестиции и финансирование: Методы оценки и обоснования. –СПб.:
Изд-во СПб ун-та, 2000.
2.
Горов М.Ю., Малеев В.В. Бизнес-планирование и
инвестиционный
анализ: Как привлечь деньги. – М.: Филинъ, 2003.
3.
Идрисов А.Б., Картышев СВ., Постников А.В.
Стратегическое планирование и анализ эффективности инвестиций. –
М.: Филинъ, 1997.
4.
Ковалев В.В. Методы оценки инвестиционных
проектов. – М.: Финансы и статистика, 2004.
5.
Ковалев В.В. Финансовый анализ: Управление
капиталом. Выбор инвестиций. Анализ отчетности. – М.: Финансы и статистика,
2002.
6.
Курс экономики I Под ред. Б.А. Райзберга. - М.:
ИНФРА-М, 1997.