Вариант 1

1.    Порядковая шкала — метрическая шкала, отображающая наряду с отношением эквивалентности еще и отношение порядка. Каждый элемент по выраженности шкалируемого признака сопоставляется с другими, но без использования единицы измерения; для такой шкалы возможно любое монотонное преобразование. По порядковой шкале ставятся оценки успеваемости в школе, порядковой является шкала твердости минералов Мосса, по этой же шкале выставляются баллы на спортивных соревнованиях и т.д.

2.     Примеры распределений

а) Биноминальное распределение.

Функция F(x) дискретной случайной величины Х, определяется формулой .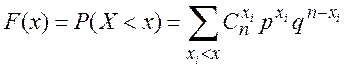

          б) Распределение Пуассона.

      Функция F(x) дискретной случайной величины Х, определяется формулой   .    .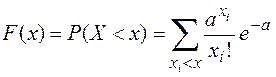

          в) Геометрическое распределение.

      Геометрическое распределение представляет собой распределение случайной величины Х- число независимых экспериментов, которое нужно выполнять до первого появления события А. Если событие наступило в k-ом испытании, то Р(Х=к)=

  

3. По таблице данных

а) проранжировать данные по возрастанию;

б) распределить по частотам;

в) сгруппировать по частотам;

г) интерпретировать полученные результаты целиком или в выбранной группе;

д) определить 25 процентиль данного распределения;

е) построить гистограмму распределения.

Таблица данных

№	Значение	№	Значение	№	Значение	№	Значение
1	1	6	6	11	3	16	6
2	5	7	5	12	7	17	8
3	4	8	2	13	8	18	4
4	6	9	3	14	2	19	7
5	4	10	4	15	7	20	6

а) 8 8 7 7 7 6 6 6 5 5 4 4 4 4 3 3 2 2

б) Число 8 встречается 2 раза, число 7 – 3 раза, число 6 – 3 раза, число 5 – 2 раза, число 4 – 4 раза, число 3 – 2 раза, число 2 – 2 раза.

в) группировка по частотам

Х – значение	2	3	4	5	6	7	8
n – частота	2	2	4	2	3	3	2

г) Наибольшую частоту имеет значение 4. Большие значения частот встречаются в середине выборки. Крайние значения имеют меньшие частоты.

д) 25-я процентиль переменной - это такое значение (x_p), что 25% (p) значений переменной попадают ниже этого значения. 25 процентиль данного распределения

е) Полигон распределения:

 

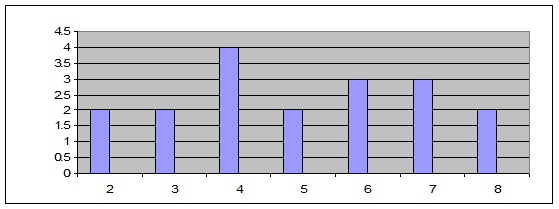
4. Число вариант в выборке нечетно, значит медиана данного распределения .

Мода-наблюдение выборки, имеющее наибольшую частоту. Для данного распределения мода .

Итак, медиана данного распределения равна 5, наибольшую частоту имеет значение 4, среднее значение данного распределения 5,06, т.е. среднее значение почти совпадает с модой.

5. Коэффициенты Пирсона

Х	37	47	40	60	61
У	60	86	67	92	95

 

N	xi	yi	xi -	(xi - )2	yi -	(yi - )2	(xi-)( yi-)
1	37	60	-12	144	-20	400	240
2	47	86	-2	4	6	36	-12
3	40	67	-9	81	-13	169	117
4	60	92	11	121	12	144	132
5	61	95	12	144	15	225	180
	245	400	0	494	0	974	657

 

Вычислим средние   и

Вычислим выборочный коэффициент корреляции по формуле

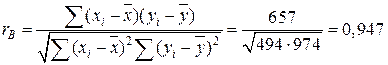
Уравнение регрессии У на Х : 

  , где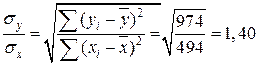 

y-80=0,947×1,40(x-49)

y= 1,33x+145,16

Представим графически уравнение регрессии Y на X и линию тренда

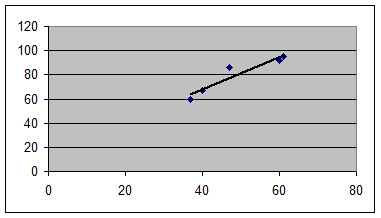
Уравнение регрессии Х на У : 

  , где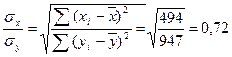 

х-49=0,947·0,72(у-80)

х= 0,68у+103,72.

         Представим графически уравнение регрессии X на Y и линию тренда

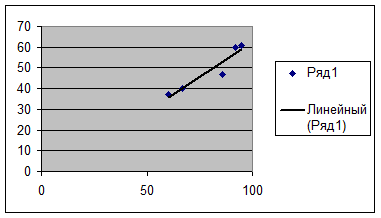
6. Х- скорость на первом участке дороги.

    У- скорость на втором участке дороги.

№	Х	У	№	Х	У
1	62	85	6	62	95
2	65	89	7	75	83
3	61	83	8	70	87
4	71	92	9	62	83
5	63	85	10	71	90

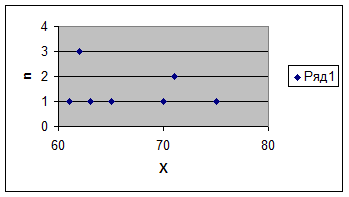
Составим закон распределения.

Х	61	62	63	65	70	71	75
n	1	3	1	1	1	2	1

Число вариант  равно 7, m=4, 

Мода-наблюдение выборки, имеющее наибольшую частоту. .

У	83	85	87	89	90	92	95
n	3	2	1	1	1	1	1

Число вариант  равно 7, m=4, 

Мода-наблюдение выборки, имеющее наибольшую частоту. .

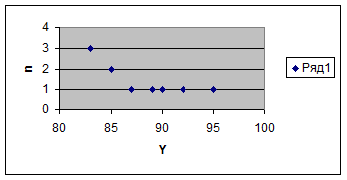         Средняя скорость на первом участке гораздо ниже чем на втором. Мода и медиана на первом участке различаются незначительно, на втором участке различия  более значительные.