Содержание:
Задание 1. 3
Задание 2. 4
Задание 3. 5
Задание 4. 8
Задание 5. 8
Задание 6. 12
Список используемой литературы.. 15
Задание 1
Приведите примеры
порядковых шкал
В соответствии с РТИ при
математическом моделировании реального явления или процесса следует, прежде
всего, установить, в каких типах шкал измерены те или иные переменные. Тип
шкалы задает группу допустимых преобразований.
Укажем основные виды шкал
измерения и соответствующие группы допустимых преобразований.
В шкале наименований (другое название - номинальной) допустимыми являются все
взаимно-однозначные преобразования (т.е. числа используются лишь как метки,
например, номера телефонов), в порядковой
- все строго возрастающие преобразования, в
шкале интервалов - линейные возрастающие преобразования, в шкале отношений - подобные (изменяющие
только масштаб) преобразования, а для абсолютной
шкалы допустимым является только тождественное преобразование.
Оценки экспертов, как уже
отмечалось, часто следует считать измеренными в порядковой шкале. Типичным
примером являются задачи ранжирования и классификации промышленных объектов,
подлежащих экологическому страхованию. Почему мнения экспертов естественно
выражать именно в порядковой шкале? Как показали многочисленные опыты, человек
более правильно (и с меньшими затруднениями) отвечает на вопросы качественного,
например, сравнительного, характера, чем количественного. Так, ему легче
сказать, какая из двух гирь тяжелее, чем указать их примерный вес в граммах.
Другими известными примерами порядковых шкал являются: в медицине - шкала
стадий гипертонической болезни по Мясникову, шкала степеней сердечной недостаточности
по Стражеско-Василенко-Лангу, шкала степени выраженности коронарной
недостаточности по Фогельсону; в минералогии - шкала Мооса (тальк - 1, гипс -
2, кальций - 3, флюорит - 4, апатит - 5, ортоклаз - 6, кварц - 7, топаз - 8,
корунд - 9, алмаз - 10), по которому минералы классифицируются согласно
критерию твердости; в географии - бофортова шкала ветров ("штиль",
"слабый ветер", "умеренный ветер" и т.д.). При оценке
качества продукции и услуг, в квалиметрии популярны порядковые шкалы (годен -
не годен, есть значительные дефекты - только незначительные дефекты - нет
дефектов). Порядковая шкала используется и в иных областях.
Порядковая шкала и шкала
наименований - шкалы качественных признаков. Поэтому во многих конкретных
областях результаты качественного анализа можно рассматривать как измеренные по
этим шкалам.[1]
Задание 2
Приведите примеры
распределения дискретных величин
При рассмотрении сложных систем нет возможности описать с помощью
математических соотношений все обстоятельства, которые влияют на характеристики
системы. Это слишком усложнило бы систему. Поэтому влияние факторов внешней
среды заменяют случайными величинами.
Реализация случайных величин - наблюдаемое конкретное значение
случайной величины. Случайные величины могут образовывать последовательности
или совокупности.
Примеры:
1) количество фраз входной информации, поступающей ежеминутно на
вход ЭВМ (последовательность случайных величин)
2) поступление различных видов груза, подлежащих отправке с ж/д
станции за один и тот же промежуток времени (совокупность случайных величин).[2]
Наиболее распространёнными типами распределений дискретных случайных
величин являются следующие:
1.
Равномерное PK=1/n при k=1,
2,…n; PK=0 при k>n.
2. Распределение
Бернулли (для двоичных случайных величин). P0=1-P; P1=P, PK=0 при k>1.
3. Распределение Пуассона
PK= lke-l/k!, 0< l <+
¥, k=0, 1, 2, 3,…
4. биномиальное
PK=СKnPK(1-P)n-k-1
при
k=0,1,…n
PK=0 при k>n, 0<p<1, n – целое.
5.
геометрическое
PK=P(1-P)K, k=0, 1, 2,… , 0<p<1[3]
Задание 3
Приведена таблица данных:
Таблица 1.
Исходные
данные
|
№
|
Значение
|
№
|
Значение
|
№
|
Значение
|
№
|
Значение
|
|
1
|
8
|
6
|
4
|
11
|
9
|
16
|
7
|
|
2
|
6
|
7
|
9
|
12
|
8
|
17
|
8
|
|
3
|
6
|
8
|
7
|
13
|
5
|
18
|
6
|
|
4
|
5
|
9
|
6
|
14
|
7
|
19
|
7
|
|
5
|
7
|
10
|
3
|
15
|
4
|
20
|
5
|
А) проранжировать данные по возрастанию.
Б) распределить по частотам,
В) сгруппировать по частотам,
Г) интерпретировать полученные
результаты целиком или в выбранной Вами группе,
Д) определить 25 процентиль данного
распределения,
Е) построить гистограмму
распределения.
Решение:
А) проранжированный ряд представлен в
таблице 2.
Б) Распределение по частотам
представлено в таблице 2.
Таблица 2.
Проранжированный
ряд
|
Ранжированный ряд
|
3
|
4, 4
|
5, 5, 5
|
6, 6, 6, 6
|
7, 7, 7, 7, 7
|
8, 8, 8
|
9, 9
|
|
Частота
|
1
|
2
|
3
|
4
|
5
|
3
|
2
|
В) Если группировать
полученные данные по частотам, то получается 5 групп.
Оформим группировку в
таблицу 3.
Таблица 3.
Группировка
по частотам
|
№ группы
|
Группа по частотам
|
№ единицы совокупности
|
Значения
|
|
1
|
1
|
10
|
3
|
|
2
|
2
|
6
|
4
|
|
7
|
9
|
|
11
|
9
|
|
15
|
4
|
|
3
|
3
|
1
|
8
|
|
4
|
5
|
|
12
|
8
|
|
13
|
5
|
|
17
|
8
|
|
20
|
5
|
|
4
|
4
|
2
|
6
|
|
3
|
6
|
|
9
|
6
|
|
18
|
6
|
|
5
|
5
|
5
|
7
|
|
8
|
7
|
|
14
|
7
|
|
16
|
7
|
|
19
|
7
|
|
Итого:
|
|
|
20
|
Г) По группировке
получилось пять групп. Частоте, равное 1, соответствует один член
распределения, частоте, равной 2 – четыре члена распределения, частоте, равной
3 – шесть членов распределения, частоте, равной 4 – четыре члена и, наконец,
последняя группа, соответствующая частоте 5, состоит из пяти членов
распределения.
Д) 25-я процентиль (также
называемая квантилью 25 или нижней квартилью) переменной - это такое значение (xp),
что 25% (p) значений переменной попадают ниже этого значения.
25 процентиль считается
по формуле:
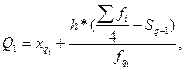 [4]
[4]
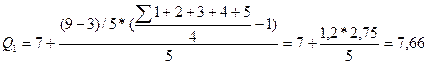
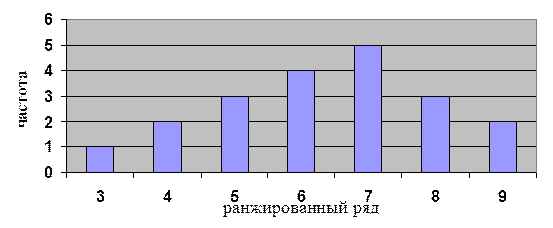
Е) Гистограмма
распределения показана на рис. 1.
|
Рис. 1.
Гистограмма распределения
|
|
Задание 4
Вычислить
для Вашего распределения (таблица 1) моду, среднее, медиану. Интерпретировать
результаты вычислений для данного распределения.
Решение:
Для
данной задачи:
Мода
– наиболее чаще встречающееся число:
Составим
ряд: 8, 6, 6, 5, 7, 4, 9, 7, 6, 3, 9, 8, 5, 7, 4, 7,
8, 6, 7, 5.
Как
видно из этого ряда мода равна 7.
 Медиана
высчитывается следующим образом:
Медиана
высчитывается следующим образом:
Ранжированный
ряд: 3, 4, 4, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 7, 8, 8, 8, 9, 9.
Для
расчета медианы нужно взять два значения, обведенные кружком.
Ме
= (6 + 7) / 2 = 6,5.
Среднее:
(3 + 4 + 4 + 5 + 5 + 5 + 6 + 6 + 6 + 6 + 7 + 7 + 7 + 7 + 7 + 8 + 8 + 8 + 9 +
9)/20 = 127/20 = 6,35.
Так
как в данном примере разбирается дискретный ряд, то мода высчитывается
простейшим методом. Медиана была высчитана для ряда, содержащего четкое
количество членов. Среднее значение распределения было рассчитано как среднее
арифметическое простое и получилось немного меньше, чем медиана.
Задание 5
Вычислить
коэффициент корреляции Пирсона, написать уравнение регрессии Y на Х и Х на Y, построить линии регрессии, используя данные таблицы
2:
Таблица 4.
Исходные данные
|
Х
|
9
|
7
|
6
|
2
|
1
|
|
Y
|
-9
|
-5
|
-3
|
-1
|
1
|
Коэффициент
корреляции Пирсона высчитывается по формуле:
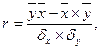 где r – парный коэффициент корреляции,
где r – парный коэффициент корреляции,
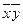 - среднее произведение
факторного и результативного признаков,
- среднее произведение
факторного и результативного признаков,
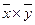 -произведение средних
размеров факторного и результативного признаков,
-произведение средних
размеров факторного и результативного признаков,
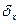 ,
, 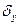 - среднее
квадратическое отклонение факторного и результативного признаков. Причем
- среднее
квадратическое отклонение факторного и результативного признаков. Причем
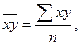
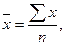
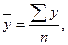
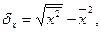
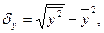
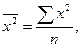
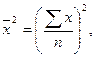
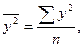
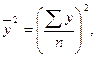 [5]
[5]
Для нахождения параметров уравнения связи и расчета
коэффициента корреляции используется вспомогательная таблица 4.
Таблица 5.
Исходные
данные для решения уравнения связи
|
Номер предприятия
|
Исходные данные
|
Расчетные данные
|
|
х
|
у
|
х2
|
у2
|
х*у
|
|
1
|
9
|
-9
|
81
|
81
|
-81
|
|
2
|
7
|
-5
|
49
|
25
|
-35
|
|
3
|
6
|
-3
|
36
|
9
|
-18
|
|
4
|
2
|
-1
|
4
|
1
|
-2
|
|
5
|
1
|
1
|
1
|
1
|
1
|
|
Итого:
|
25
|
-17
|
171
|
117
|
-135
|
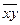 = -135/5 = 27,
= -135/5 = 27, 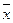 = 25/5 = 5,
= 25/5 = 5, 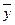 = -17/5 = 3,4,
= -17/5 = 3,4, 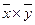 = 5*3,4 = 17,
= 5*3,4 = 17, 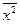 = 171/5 = 34,2,
= 171/5 = 34,2, 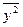 = 117/5 = 23,4,
= 117/5 = 23,4, 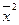 = 52 = 25,
= 52 = 25, 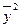 = 3,42 = 11,56,
= 3,42 = 11,56,
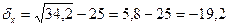 ,
, 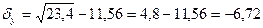 ,
,
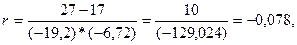
Коэффициент
корреляции отрицательный, значит связь обратная.
Нахождение корреляционного уравнения связи и
выявление зависимости между признаками.
Связь между результативным и факторным признаками
может носить линейный и криволинейный характер. При линейной форме связи
используется уравнение прямой Y
= A + Bx, где у – теоретический уровень
результативного признака (окупаемости затрат), а – начало отсчета, х –
факторный признак (производительность труда), в – коэффициент регрессии, показывающий
среднее изменение результативного признака при изменении факторного признака на
единицу.
1.
 При
линейной форме связи эта система имеет вид:
При
линейной форме связи эта система имеет вид:
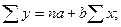
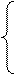
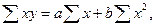 где n – численность совокупности (в данном
случае n = 5).
где n – численность совокупности (в данном
случае n = 5).
-17 = 5а
+ 25b,
-135 = 25a + 171b.
Решим эту
систему:
a = (-17 – 25b)/5, 5*(-17 – 25b) + 171b = -135, -85 – 125b + 171b = -135,
46b = -50, b = -1,1/
A = (-17 + 25*1,1)/5 = 2,1/
Тогда
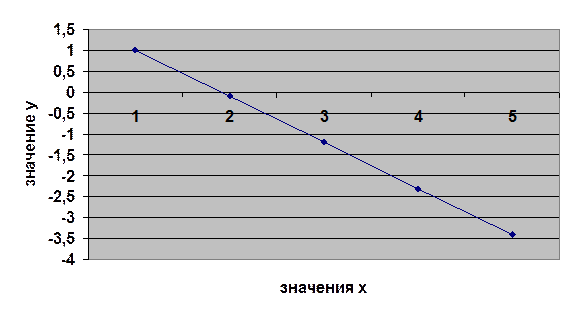
уравнение регрессии Y на Х будет равно Y = 2,1 – 1,1х.
2.
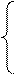 При
уравнении регрессии Х на Y
система выглядит следующим образом:
При
уравнении регрессии Х на Y
система выглядит следующим образом:

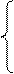
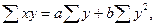 где n – численность совокупности (в данном
случае n = 5).
где n – численность совокупности (в данном
случае n = 5).
25 = 5а –
17b,
-135 =
-17a + 117b.
Решим
теперь эту систему:
А = (25 + 17b)/5, - 135 = -17 (25 + 17b)/5 + 117b = - 85 –
57,8b + 117b = 59,2b- 85.
B = (-135 + 85)/59,2 = – 50/59,2 = – 0,8.
A = (25 + 17*(-0,8))/5 = (25 –
13,6)/5 = 2,28.
Уравнение
выглядит следующим образом:
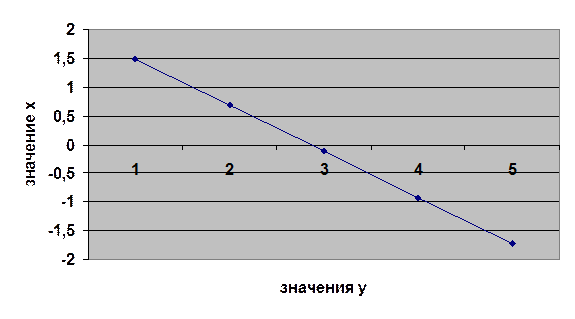
Х = 2,28
– 0,8y.
Графики
линий регрессий показаны на рис. 2 и 3.
|
Рис. 2. Уравнение
регрессии Y на Х
|
|
|
Рис. 3. Уравнение
регрессии Х на Y
|
|
Задание 6
Сделать
два измерения величины по Вашему выбору (не менее 10 замеров каждое). Выполнить
все возможные вычисления и построения. Дать сравнительный анализ полученных
измерений.
Для
данного решения были сделаны два вида замеров.
Первый
замер – десятикратное измерение обычного ластика с помощью различных линеек. Результаты
занесены в таблицу 5.
Второй
замер – десятикратное измерение пульса при помощи секундомера. Результаты также
занесены в таблицу 5.
Таблица 5.
Результаты первого и второго измерений
|
№
|
Значение
|
№
|
Значение
|
|
1
|
3,0
|
1
|
78
|
|
2
|
3,1
|
2
|
82
|
|
3
|
3,0
|
3
|
89
|
|
4
|
3,2
|
4
|
79
|
|
5
|
3,4
|
5
|
85
|
|
6
|
3,0
|
6
|
83
|
|
7
|
3,2
|
7
|
80
|
|
8
|
3,1
|
8
|
85
|
|
9
|
3,3
|
9
|
79
|
|
10
|
3,0
|
10
|
75
|
Для
каждого из этих измерений найдем моду, среднее, медиану и построим гистограммы
измерений.
Для
первого измерения:
Дискретный
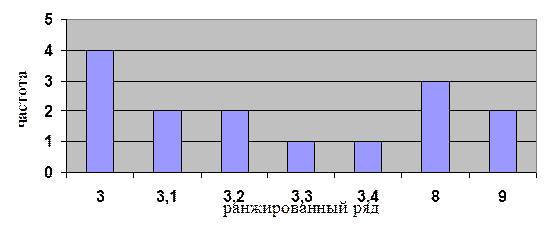
ряд = 3,0; 3,1; 3,0; 3,2; 3,4; 3,0; 3,2; 3,1; 3,3; 3,0.
Мода
= 3,0.
 Среднее
арифметическое = (3 + 3,1 + 3 + 3,2 + 3,4 + 3 + 3,2 + 3,1 + 3,3 + 3)/10 = 3,13.
Среднее
арифметическое = (3 + 3,1 + 3 + 3,2 + 3,4 + 3 + 3,2 + 3,1 + 3,3 + 3)/10 = 3,13.
Ранжированный
ряд: 3, 3, 3 , 3, 3,1, 3,1, 3,2, 3,2, 3,3, 3,4.
Медиана
= (3,1 + 3,1)/2 = 3,1.
Построим
гистограмму.
Для второго измерения:
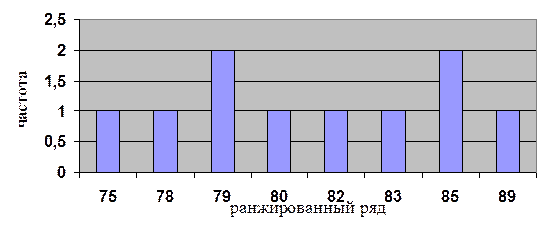
Дискретный ряд = 78, 82, 89,
79, 85, 83, 80, 85, 79, 75.
Отсюда
видно, что мода = 85 и 79.
 Среднее
арифметическое ряда = (78 + 82 + 89 + 79 + 85 + 83 + 80 + 85 + 79 + 75)/10 =
81,5.
Среднее
арифметическое ряда = (78 + 82 + 89 + 79 + 85 + 83 + 80 + 85 + 79 + 75)/10 =
81,5.
Ранжированный
ряд для нахождения медианы: 75, 78, 79, 79, 80, 82, 83, 85, 85, 89.
Медиана
= (80 + 82)/2 = 81.
Построим
гистограмму:
Из расчетов видно, что
если измерения зависят от инструмента, то результаты более или менее стабильны,
а если измерения зависят от человеческих факторов, то здесь разброс значений
довольно велик и зависит от ситуации.
Список
используемой литературы
1.
Елисеева И.И., Юзбашев М.М. Общая теория статистики. –
М.: «Инфра-М», 1999.
2.
Ефимова М.Р. Общая теория статистики. – М.:
«Мира-люкс», 2002.
3.
Общая теория статистики/Под ред. Спирина И.А.. – М.:
«Инфра-М», 2001.
4.
Башет К.В. Статистика коммерческой деятельности. – М: Финансы и статистика. 1996 г.
5.
Вопросы статистики 1996 г. №1, №11.
6.
Вопросы статистики 1997 г. №2, №4, №5.
7.
Елесеева М.А. Общая теория статистики.– М.: Статистика,
1988.
8.
Харченко Л.П. Статистика. – М: ИНФРА, 1997.
9.
www.nisse.ru/analitics.html?id=managment&part=5
10.
http://old.sgu.ru/kafedra/teorin/Lekciya_206.htm
[1] www.nisse.ru/analitics.html?id=managment&part=5
[2] Ефимова М.Р. Общая теория
статистики. – М.: «Мира-люкс», 2002.
[3] http://old.sgu.ru/kafedra/teorin/Lekciya_206.htm
[4] Общая теория
статистики/Под ред. Спирина И.А.. – М.: «Инфра-М», 2001.
[5] Общая теория
статистики/Под ред. Спирина И.А.. – М.: «Инфра-М», 2001.