Глава 7. Строение мицеллы гидрофобного золя. Коагуляция гидрофобного золя

Синтез гидрофобных дисперсных систем (суспензий, золей, в том числе аэрозолей, эмульсий) осуществляют методами диспергирования и конденсации. Диспергирование твердых и жидких веществ в выбранных средах проводят в шаровых и коллоидных мельницах вибропомола, ультразвуковых установках и др. Эффект усиливается при введение в среду ПАВ (эффект Ребиндера). Конденсационные методы основаны на физической или химической конденсации атомов или молекул с последующим образованием новой фазы в виде дисперсных частиц, распределенных в объёме среды (газообразной, жидкой или твердой).

 Методом физической конденсации получают золи, дымы, дисперсные металлы. При химической конденсации частицы новой фазы образуются в результате протекания в системе химической реакции с образованием малорастворимых соединений.

Гидрофобные  дисперсные системы термодинамически неустойчивы, так как частицы дисперсной фазы склонны к агрегации. Их термодинамическая агрегативная неустойчивость обусловлена избытком поверхностной энергии. Межфазное поверхностное натяжение в гидрофобных системах больше рассчитанного по соотношению Ребиндера-Щукина. Поэтому они не могут быть получены самопроизвольным диспергированием как лиофильные системы; для их образования должна быть затрачена внешняя энергия.

Укрупнение частиц дисперсной фазы при потере агрегативной устойчивости достигается в результате изотермической перегонки (растворение мелких и рост крупных частиц в соответствии с уравнением Кельвина) или за счет слипания (слияния) частиц – коагуляции. Наиболее распространен процесс коагуляции. В зависимости от природы системы и концентрации дисперсной фазы этот процесс может заканчиваться или осаждением частиц, или структурообразованием.

Гидрофобные дисперсные системы характеризуются кинетической агрегативной устойчивостью, определяемой скоростью процесса коагуляции. Кинетика коагуляции определяется уравнением Смолуховского:

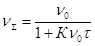                или          

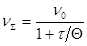
где 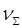 - суммарное число частиц дисперсной фазы ко времени τ; 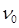 - первоначальное число частиц; 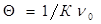 - время половинной коагуляции; К – константа скорости коагуляции.

Константа К определяется соотношением

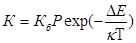                                  или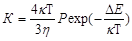            

где К_б – константа скорости быстрой коагуляции; Р – стерический множитель, учитывающий благоприятные пространственные расположения частиц при столкновении; ΔЕ – энергия взаимодействия частиц, или потенциальный барьер; κ -  константа Больцмана; η – вязкость дисперсионной среды.

Константа скорости коагуляции К (константа скорости медленной коагуляции) является мерой кинетической агрегативной устойчивости. Если ΔЕ=0 и Р=1, то эта константа равна константе скорости быстрой  коагуляции, зависящей от вязкости среды и температуры системы. Если ΔЕ≠0 и Р≠1, то не все соударения частиц эффективны, и происходит медленная коагуляция. Замедление коагуляции, обусловленное  потенциальным барьером, характеризуется фактором устойчивости, или коэффициентом стабильности:

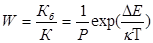
При значительном потенциальном барьере может наступить такое состояние системы, когда скорость агрегации частиц равна скорости дезагрегации и система окажется термодинамически устойчивой к коагуляции.

Таким образом, агрегативная устойчивость коллоидных систем обуславливается термодинамическими и кинетическими факторами. Термодинамические факторы, действие которых направлено на снижение поверхностного натяжения и увеличение энтропии, уменьшают вероятность эффективных соударений между частицами, создают потенциальные барьеры. Кинетические факторы снижают скорость столкновения частиц и связаны в основном с гидродинамическими свойствами системы.

Различают следующие факторы устойчивости (стабилизации) дисперсных систем.

1. Электростатический фактор (термодинамический); заключается в уменьшении поверхностного натяжения вследствие возникновения двойного электрического слоя на поверхности частиц в соответствии с уравнением Липпмана. 2. Адсорбционно-сольватный фактор (термодинамический); состоит в уменьшении поверхностного натяжения в результате взаимодействия частиц с дисперсной средой (уравнение Дюпре) или благодаря адсорбции стабилизаторов (адсорбционное уравнение Гиббса). 3. Энтропийный фактор (термодинамический); проявляется в стремлении дисперсной фазы к равномерному распределению по объёму систему под действием теплового движения. 4. Структурно-механический фактор (кинетический); связан с тем, что на разрушение пленок, образующихся на поверхности частиц и обладающих упругостью и механической прочностью, требуется энергия и время. 5. Гидродинамический фактор (кинетический); заключается в снижении скорости движения частиц при изменении вязкости и плотности дисперсионной среды.       6. Смешанные факторы наиболее характерны для реальных систем; агрегативная устойчивость обеспечивается действием нескольких факторов одновременно.

Каждому фактору устойчивости соответствует специфический метод его нейтрализации. Например, электростатический фактор очень чувствителен к введению электролитов. Действие структурно-механического фактора можно предотвратить с помощью веществ, разжигающих упругие структурированные слои на поверхности частиц, а также механическим, термическим способами и др.

Устойчивость дисперсных систем определяется балансом энергии притяжения и энергии отталкивания между частицами. По теории ДЛФО (Дерягина, Ландау, Фервея, Овербека), учитывающей только электростатическую составляющую расклинивающего давления (давления отталкивания), энергия отталкивания убывает с расстоянием по экспоненциальному закону.

Для области малых электрических потенциалов суммарная энергия взаимодействия частиц (пластин) равна

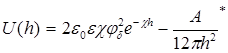
где φ_δ – электрический потенциал диффузного слоя; χ – величина, обратная толщине диффузного слоя; А^* - константа Гамакера; h – расстояние между частицами (пластинами); ε – диэлектрическая проницаемость дисперсной среды; ε₀ – электрическая постоянная.

При больших потенциалах и расстояниях между частицами (пластинами) эта энергия определяется уравнением

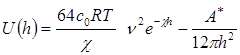
Суммарная потенциальная энергия взаимодействия частиц отрицательна на близких и далеких расстояниях (преобладает энергия притяжения). Она может быть положительна на средних расстояниях (преобладает энергия отталкивания). Максимум потенциальной кривой (рис 1.) отвечает потенциальному барьеру ΔЕ. Первый минимум I соответствует непосредственному соприкосновению частиц, а второй II – притяжению частиц, между которыми имеются прослойки среды.

Коагуляция гидрофобных дисперсных систем может происходить в результате различных внешних воздействий, например при механическом воздействий (ультразвука), действии электрического поля, при нагревании или замораживании системы. Коагуляция гидрофобных золей может быть вызвана также их сильным разбавлением или концентрированием. Наиболее часто коагуляция дисперсных систем происходит при добавлении электролитов. Различают два типа электролитной коагуляции коллоидных систем: 1) нейтрализационную, происходящую в результате снижения поверхностного потенциала частиц; 2) концентрационную, протекающую вследствие сжатия диффузной части двойного электрического слоя (потенциал поверхности в этом случае не изменяется).

Нейтрализационная электролитическая коагуляция характерна для коллоидных систем, содержащих слабо заряженные частицы. Концентрационная коагуляция обычно наблюдается в сильно заряженных дисперсных системах.

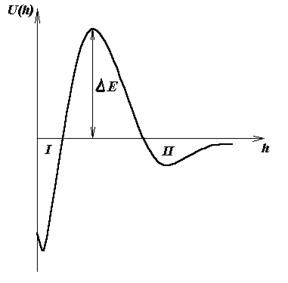
Рис.1. Зависимость энергии взаимодействия U двух частиц от расстояния между ними h.

.

Введение электролитов снижает высоту потенциального барьера, но при небольших концентрациях электролита энергетический барьер остается достаточно велик и коагуляция не происходит. Агрегация наступает при введении определенного для данной системы количества электролита, соответствующего порогу коагуляции. Порок быстрой коагуляции с_к   определяет количество электролита, необходимое для коагуляции единицы объёма коллоидной системы при полном исчезновении потенциального барьера ΔЕ. При сохранении  небольшого потенциального барьера в системе протекает медленная коагуляция.

При электролитной коагуляции по концентрационному механизму (для сильно заряженных частиц) порок коагуляции с_к  в соответствии с правилом Дерягина-Ландау (обоснование эмпирического правила Шульца-Гарди) обратно пропорционален заряду z противоионов в шестой степени, т. е.

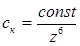
При нейтрализационной коагуляции (при малых потенциалах поверхности φ₀ частиц) показатель степени  z в уравнении уменьшается до двух (правило Эйлерса-Корфа).      

Строение коллоидной мицеллы схематически может быть изображено на примере мицеллы иодида серебра:

{[(AgI)_n                                  mI^-]                                xK⁺}                             (m-x)K⁺

Агрегат или кристаллик твердого вещества

Потенциалопределяющие ионы

Ионы адсорбционного слоя

Ионы диффузного слоя

                         ядро 

                                                   частица

                                                                                мицелла    

Примеры решения задач.

 

 1. Определите, к какому электроду должны перемещаться частицы золя, получаемого при реакции при небольшом избытке H₂S:

2H₃AsO₃+3H₂S=As₂S₃+6H₂O

Решение. Потенциал определяющими ионами в данном случая могут быть ионы SH^- , так как в состав агрегата входят ионы серы. Состав адсорбционного слоя могут входить ионы Н⁺. Ионы Н⁺ образуют диффузный слой. Таким образом, схематическое строение мицеллы золя можно выразить следующей формулой:

{[( As₂S₃)_m·n SH^-]· Н⁺}(n-x) Н⁺

Частица имеет отрицательный заряд, - следовательно, электрофоретическое движение направлено к аноду.

 2. Время половинной коагуляции золя иодида серебра при исходном содержании частиц в 1 м³, равном 3,2·10¹⁴, составляет 11,5 с. Определите константу скорости коагуляции.

Решение. Расчет проводим, используя формулу, связывающую константу скорости коагуляции с временем половинной коагуляции:

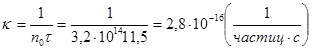
 3. Золь иодида серебра, получаемый по реакции:

KI+AgNO₃→AgI+KNO₃

при некотором избытке KI , коагулируют растворами сульфата калия и ацетата кальция. Коагулирующее действие какого электролита сильнее?

Решение. Строение мицеллы золя таково:

{[( AgI)_m·nI^-]xK⁺}(n-x)K⁺

Ионами, образующими диффузный слой, т.е. противоионами, являются катионы K⁺. Следовательно, при сравнении коагулирующего действия необходимо сравнивать заряды катионов вводимого электролита. Так как заряд иона Са²⁺ выше заряда иона  K⁺ , то в соответствии с правилом Шульце-Гарди коагулирующее действие Са(СН₃СОО)₂ сильнее.

 

Задачи

1. Золь AgI получен при добавлении 8 мл водного раствора КI кон­центрацией 0,05 моль/л к 10 мл водного раствора AgNO₃ концентрацией 0,02 моль/л. Напишите формулу мицеллы образовавшегося, золя. Как заряжена частица золя?

2. Золь гидроксида железа (III) получен при добавлении к 85 мл кипящей дистиллированной воды 15 мл 2%-ного раствора хлорида железа(III). Напишите формулу мицелл золя Fе(ОН)₃, учитывая, что при образовании частиц гидроксида железа(Ш) в растворе присут­ствуют следующие ионы Fе⁺³, СI^-. Как заряжены частицы золя?

3. Во сколько раз уменьшится суммарное число частиц ν_Σ мартеновских печей через 1, 10, 100 с после начала коагуляции? Сред­ний радиус частиц 20 нм, концентрация 1·10 ^-3 кг/м³, плотность частиц 2,2 г/см³. Константа быстрой коагуляции, по Смолуховскому, равна 3·10 ^-16 м³/с.

4. При исследовании коагуляции полистирольного латекса полу­чены следующие значения порогов коагуляции:

Электролит	NaCI	CaCI2	AICI3
Порог коагуляции, моль/л	0,47	8,8·10-3	6·10-4

Рассчитайте соотношение порогов коагуляции и сопоставьте его с со­отношением, получаемым в соответствии с правилом Дерягина - Ландау.

5. Порог коагуляции отрицательно заряженного гидрозоля As₂S₃  под действием КСI равен 4,9·10 ^-2 моль/л. С помощью правил Шуль­це - Гарди и Дерягина - Ландау для этого золя рассчитайте пороги коагуляции, вызываемой следующими электролитами: К₂S0₄, MgCI₂, MgSO₄, А1С1₃ и А1₂(S0₄)_3.

 

6. Порог  коагуляции  положительно заряженного  гидрозоля Fе(ОН)з под действием электролита NaCI равен 9,25 ммоль/л. С по­мощью правил Шульце - Гарди и Дерягина - Ландау для этого золя рассчитайте пороги коагуляции, вызываемой следующими электроли­тами: KNO_3, BaCI₂ , K₂S0 ₄, MgS0₄, К ₂Cr₂O_7.

7. Порог коагуляции гидрозоля металлического золота, вызывае­мой NaCI, равен 24 ммоль/л, a K₂S0₄ - 11,5 ммоль/л. Используя пра­вила Шульце - Гарди и Дерягина - Ландау, определите знак заряда золя и рассчитайте порог коагуляции для, следующих электролитов; СаСI₂ , MgS0_4, АI₂(S0₄)₃, АIСI₃, Th(NO₃)₄.

8. Напишите схему строения мицелл сульфида цинка, образующихся при получении золя: а) в случае избытка ZnSO₄; б) в случае избытка (NH₄)₂SO₄, по следующей реакции:

ZnSO₄+(NH₄)₂S=ZnS+(NH₄)₂SO_4.

 

9_. Напишите схему строения мицеллы сульфата бария, получающегося при взаимодействии хлорида бария с некоторым избытком сульфата натрия.

10. Укажите, к какому электроду должны двигаться частицы гидроксида алюминия, образующиеся при  гидролизе. Принять, что гидролиз протекает неполно:

AICI₃+H₂O=AI(OH)₃+3HCI.

11. В воде содержатся ультрамикроскопические радиоактивные частицы. Для очистки воды от них предложено вводить электролиты: хлорид алюминия или фосфат калия. Предварительно установлено, что частицы при электрофорезе движутся к катоду. Какой электролит следует предпочесть в данном случае?

12. Золь гидроокиси железа, получаемый неполным гидролизом хлорного железа, коагулируют растворами сульфида натрия, хлорида натрия и хлорида бария. Какой из электролитов окажет наиболее значительное коагулирующее действие?

13. Изучение быстрой коагуляции суспензии каолина,  проводимое путем счета частиц с помощью ультрамикроскопа, дало следующие результаты:

Время коагуляции, с	0	105	180	255	335	420
Общее кол-во частиц в 1 м3 золя, 10-14	5,0	3,90	3,18	2,92	2,52	2,00

Рассчитайте по приведенным данным время половинной коагуляции.

14-27. Написать строение мицеллы золя, полученного по реакции. Определить к какому электроду будет двигаться коллоидная частица:

14. AI(OH)₃, стабилизированный AICI₃. 

15. SiO₂, стабилизированный H₂SiO₃.

16. Au, стабилизированный КAuO₂.

17. As₂S₃, стабилизированный H₂S.

18. Ba(OH)₂ ,стабилизированный BaCI₂.

19. PbS , стабилизированный Pb(NO₃)_2.

 

20. FeS , стабилизированный Fe₂(SO₄)₃.

21. CrO₃ ,  стабилизированный H₃CrO₆.

22. Ni(OH)_{2 ,} стабилизированный  Ni(NO₃)_2.

 

23. Pt  , стабилизированный H₃(PtCI)₆.

24. BaCI₂+Na₂ SO₄=BaSO₄+2NaCI ; в избытке Na₂SO_4.

 

25. ZnSO₄+(NH₄)₂S=ZnS+(NH₄)₂SO₄ ;  в избытке (NH₄)₂S.

26. Время половинной коагуляции тумана минерального масла с удельной поверхностью 1,5*10⁷ м^-1 , концентрацией 25 мг/л составляет 240 с. Рассчитайте и постройте кривую изменения суммарного числа частиц при коагуляции для следующих интервалов времени: 60, 120, 240, 480 и 600 с. Плотность масла 0,970 г/см³.

27. При изучении оптическим методом кинетики электролитной коагуляции гидрозоля AgJ, стабилизированного ПАВ, получено значение константной скорости быстрой коагуляции, равное 3,2*10^-18м³/с (при 293К). Вязкость среды 1*10^-3Па*с. Сравните эту константу с константой, даваемой теорией Смолуховского. Объясните влияние ПАВ на характер коагуляции.

28. По экспериментальным данным время половинной коагуляции гидрозоля составляет340 с при исходной частичной концентрации частиц 2,52*10¹⁴част/м³, вязкости дисперсионной среды 1*10^-3Па*с, и температуре 293 К. Сделайте вывод, быстрой или медленной является коагуляция, если вязкость среды увеличить в 3 раза.

29. Во сколько раз уменьшится суммарное число частиц 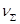 дыма мартеновских печей через 1, 10, 100 с после начала коагуляции? Средний радиус частиц 20 нм, концентрация 1*10^-3 кг/м³, плотность частиц 2,2 г/см³. Константа быстрой коагуляции по Смолуховскому равна 3*10^-16м³/с.

30. Рассчитайте константу быстрой коагуляции золя серы среды под действием хлорида алюминия, используя следующие экспериментальные данные:

         τ, с                              0          2          4          10

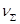         *10^-17, част/м³         16,0     0,99     0,50     0,20

31. Рассчитайте время половинной коагуляции, используя экспериментальные данные по изменению общего числа частиц при коагуляции ……………… дисперсной системы в воде:

         τ, с                              0          7,0       15,0     20,2     28,0

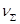         *10^-15, част/м³       32,2     24,2     19,9     16,7     14,2

32. Проверьте применимость теории Смолуховского к коагуляции золя селена раствором хлорида калия, используя следующие экспериментальные данные:

         τ, с                              0          0,66     4,25     19,0     43,0

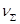         *10^-14, част/м³       29,70   20,90   19,10   14,40   10,70

33. Рассчитайте число первичных частиц гидрозоля золота при коагуляции электролитом к моменту времени τ=150с, если первоначальное число частиц в 1м³ составляет 1,93/10¹⁴, а константа скорости быстрой коагуляции равна 0,2*10¹⁷м³/с.

34. Рассчитайте константу скорости быстрой коагуляции суспензии каолина в воде по данным кинетики коагуляции, полученным с помощью ультрамикроскопа (при 293 К)

         τ, с                              0          100      175      250      400      500

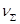         *10^-14, част/м³       5,0       3,78     3,23     2,86     2,22     1,96

35. При изучении коагуляции суспензии ………… …………. в воде методом счета частиц в ультрамикроскопе получены следующие данные:

         τ, с                              335      510      600      800

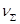         *10^-14, част/м³       2,52     1,92     1,75     1,49