Вариант Н, К.
|
№ п/п
|
Х, млн. руб.
|
Y, тонн
|
|
1
|
9,5
|
23,9
|
|
2
|
10,3
|
24,7
|
|
3
|
7,9
|
22,4
|
|
4
|
5,6
|
25,1
|
|
5
|
6,1
|
27,0
|
|
6
|
6,8
|
29,4
|
|
7
|
4,2
|
34,2
|
|
8
|
3,5
|
30,6
|
|
9
|
3,2
|
35,2
|
|
10
|
2,0
|
34,0
|
Задача 1. Построить модель связи между указанными факторами, проверить
её адекватность, осуществить точечный и интервальный прогноз.
1) Исходные данные
нанесите на координатную плоскость и сделайте предварительное заключение о
наличии связи между Х и Y, а также о её виде (прямая или обратная) и форме (линейная и
нелинейная).
По горизонтальной оси –
стоимость основных производственных фондов – Х, млн. руб; по вертикальной –
среднесуточная производительность – Y,тонн.
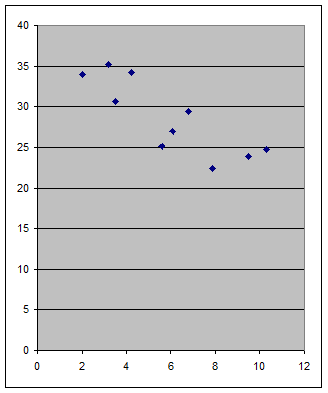
Проанализировав поле рассеяния
можно сделать вывод о том, что связь между признаками является линейной и
обратной.
2) 
|
№
|
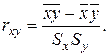
хi
|
yi
|
xiyi
|
|
|
|
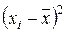
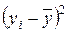
1
|
9,5
|
23,9
|
227,05
|
12,8881
|
22,5625
|
|
2
|
10,3
|
24,7
|
254,41
|
19,2721
|
15,6025
|
|
3
|
7,9
|
22,4
|
176,96
|
3,9601
|
39,0625
|
|
4
|
5,6
|
25,1
|
140,56
|
0,0961
|
12,6025
|
|
5
|
6,1
|
27,0
|
164,7
|
0,0361
|
2,7225
|
|
6
|
6,8
|
29,4
|
199,92
|
0,7921
|
0,5625
|
|
7
|
4,2
|
34,2
|
143,64
|
2,9241
|
30,8025
|
|
8
|
3,5
|
30,6
|
107,1
|
5,8081
|
3,8025
|
|
9
|
3,2
|
35,2
|
112,64
|
7,3441
|
42,9025
|
|
10
|
2,0
|
34,0
|
68
|
15,2881
|
28,6225
|
|
∑
|
59,1
|
286,5
|
1594,98
|
68,409
|
199,245
|
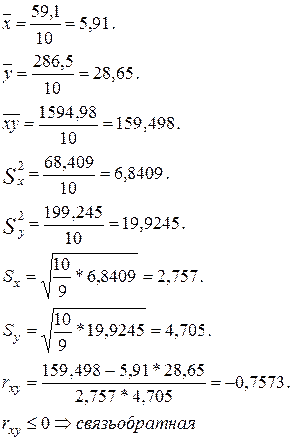
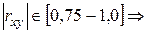связь между признаками линейная, сильная.
Проверим значимость rxy , используя критерий Стьюдента.
Гипотезы:
Н0 –
корреляция между признаками отсутствует;
Н1 – между
признаками существует корреляционная зависимость.
Фактическое значение t-критерия
Табличное значение
= 0,05
К = N – 2 = 8
T0,05; 8 = 2,31.
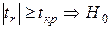отвергается
между признаками
существует корреляционная зависимость.
3) уравнение регрессии
имеет вид
yi = О0 +
О1xi
Система нормальных
уравнений для оценки параметров θ0 и θ1.
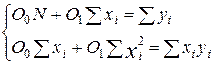
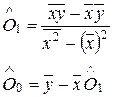
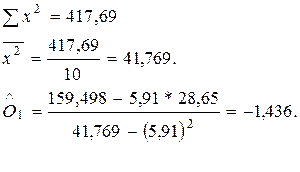
4) проверим
значимость параметра О0
Н0 – параметр
О0 не является значимым;
Н1 – параметр
О0 является значимым.
где:
mО0 – стандартная ошибка параметра О0.
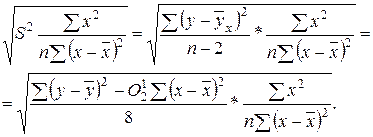
mO0
mO0 = 
tO0 =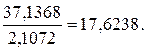 
Табличное значение
t = 2,31.
tO0 ≥ t Н0
отвергается; параметр О0 является значимым.
Проверим значимость
параметра О1
tO1 =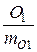 
mO1 – стандартная ошибка параметра О1.
mO1 =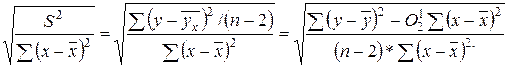 
mO1 =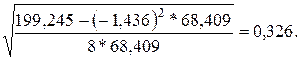 
tO1 = 
Табличное значение t-критерия
t = 2,31.
Н0 отвергается; параметр О1 является
значимым.
Т.к. оба параметра
уравнения регрессии являются значимыми фактор х оказывает влияние
на величину у.
5) Гипотезы:
Н0 – фактор х
не оказывает влияние на у;
Н1 – фактор х
оказывает влияние на у.
Рассчитаем фактическое
значение F-критерия.
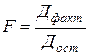
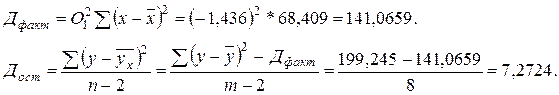
F =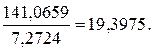 
Табличное значение
F = 0,05 = 6,61.
F = 0,01 = 16,26.
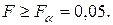
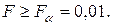
Н0 – отвергается.
уравнение регрессии
является значимым; между признаками х и у существует линейная связь.
6) Дисперсионный анализ
результатов регрессии
|
Источники вариации
|
Число степеней свободы
|
Сумма квадратов отклонений
|
Дисперсия на одну ст.
свободы
|
F - отношение
|
фактическое
|
Табличное при = 0,05
|
|
Общая
|
9
|
199,245
|
-
|
-
|
-
|
|
Объяснённая
|
1
|
141,0659
|
141,0659
|
19,3975
|
6,61
|
|
Остаточная
|
8
|
58,1791
|
7,2724
|
1
|
-
|
7) выберем прогнозную точку
хn = 11
Рассчитаем уn
yn
= 37,1368 – 1,436*11 =
21,3408.
8) доверительный интервал для
уравнения регрессии
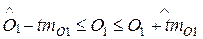
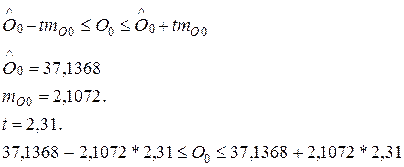
32,2692 ≤ О0 ≤
42,0044
О0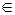 
(32,2692; 42,0044).
Доверительный интервал
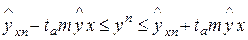
ta
= 2,57
21,3408 – 2,57 * 1,8659 ≤ уn ≤ 21,3408 + 2,57 * 1,8659
16,5454 ≤ уn ≤ 26,1362
уn 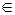(16,5454; 26,1362)
