Содержание


Введение. 3

1. Понятие геометрической прогрессии. 4

2. Процесс стандартизации параметрических рядов с помощью геометрической прогрессии. 8

3. Реформирование стандартизации по информационным технологиям. 11

Заключение. 16

Список литературы.. 17


 

Введение


Объект стандартизации (согласно ГОСТ Р 1.0) - продукция, работа, процесс и услуги, подлежащие или подвергшиеся стандартизации.

В процессе трудовой деятельности, специалисту приходится решать систематически повторяющиеся задачи:

измерение и учет количества продукции,

составление технической и управленческой документации,

измерение параметров технологических операций,

контроль готовой продукции,

упаковывание поставляемой продукции и т.д.

Существуют различный варианты решения этих задач.

Цель стандартизации - выявление наиболее правильного и экономичного варианта, т.е. нахождение оптимального решения. Найденное решение дает возможность достичь оптимального упорядочения в определенной области стандартизации. Для превращения этой возможности в действительность необходимо, чтобы найденное решение стало достоянием большого числа предприятий (организаций) и специалистов.

Только при всеобщем и многократном использовании этою решения существующих и потенциальных задач возможен экономический эффект от проведенного, упорядочения.

Цель работы – рассмотреть основы построения и преимущества рядов на основе использования геометрической прогрессии.

Задачи работы – дать понятие геометрической прогрессии; рассмотреть процесс стандартизации параметрических рядов с помощью геометрической прогрессии.

1. Понятие геометрической прогрессии

 

Прежде всего, необходимо дать определение геометрической прогрессии, ибо не определившись о предмете разговора невозможно продолжать сам разговор.

Итак: числовая последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предшествующему члену, умноженному на одно и тоже не равное нулю число, называется геометрической прогрессией.

Внесу некоторую ясность в данное выше определение:

Во-первых, мы требуем от первого члена неравенства нулю для того, что при умножении его на любое число мы в результате снова получим ноль, для третьего члена опять ноль, и так далее.

Получается последовательность нулей, которая не попадает под данное выше определение геометрической прогрессии и не будет являться предметом нашего дальнейшего рассмотрения.

Во-вторых, число на которое умножаются члены прогрессии опять же не должно быть равно нулю, по вышеизложенным причинам.

В-третьих, предоставляю возможность вдумчивому читателю самому найти ответ на вопрос, почему мы умножаем все члены прогрессии на одно и тоже число, а не, скажем, на разные. Ответ не так прост, как может показаться вначале.

Далее, из определения геометрической прогрессии следует, что отношение любого ее члена к предшествующему равно одному и тому же числу,

т. е. b2:b1 = b3:b2 = ... = bn:bn-1 = bn+1:bn = ... .

Это число называется знаменателем геометрической прогрессии и обычно обозначается буквой q.

Несколько слов необходимо сказать и о способах задания геометрической прогрессии.

Для того чтобы задать геометрическую прогрессию (bn), достаточно знать ее первый член b1 и знаменатель q.

Например, условиями b1 = 2, q = -5 (q < 0) задается геометрическая прогрессия 2, -10, 50, -250, ... .

Эта прогрессия не является ни возрастающей ни убывающей последовательностью.

Следует заметить, что:

последовательность называется возрастающей (убывающей) если каждый последующий член последовательности больше (меньше) предыдущего.

Таким образом, если q > 0 (q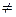1), то прогрессия является монотонной последовательностью. Пусть, например, b1 = -3, q = 4, тогда геометрическая прогрессия -3, -12, -48, -192, ... есть монотонно убывающая последовательность.

Однако, если q = 1, то все члены прогрессии равны между собой. В этом случае прогрессия является постоянной последовательностью.

Любая геометрическая прогрессия обладает определенным характеристическим свойством.

Это свойство является следствием самого правила задания геометрической прогрессии: последовательность (bn) является геометрической прогрессией тогда и только тогда, когда каждый ее член, начиная со второго, есть среднее геометрическое соседних с ним членов, т. е.

.

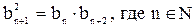Пользуясь этим свойством можно находить любой член геометрической прогрессии если известны два рядом стоящие.

Для нахождения n-ного члена геометрической прогрессии есть еще одна формула.

Для того чтобы найти любой член геометрической прогрессии необходимо, чтобы она была задана, т. е. были известны значения b1 и q:

.

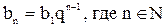Так как геометрическая прогрессия это числовая последовательность, то мы можем найти ее сумму. Для нахождения суммы геометрической прогрессии применяют следующую формулу:

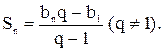
Если в данную формулу подставить вместо bn его выражение в виде b1qn-1, то получим еще одну формулу для вычисления суммы геометрической прогрессии:

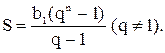
У геометрической прогрессии есть еще одно свойство, а именно: из определения знаменателя геометрической прогрессии следует, что b1bn = b2bn-1 = ..., т. е. произведение членов, равно отстоящих от концов прогрессии, есть величина постоянная.

Наконец, нельзя не коснуться такого важного с научной точки зрения понятия, как бесконечной геометрической прогрессии при 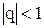. Здесь наиболее важным понятием является понятие суммы бесконечной геометрической прогрессии: пусть (xn) - геометрическая прогрессия со знаменателем q, где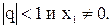  

Суммой бесконечной геометрической прогрессии, знаменатель которой удовлетворяет условию 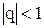, называется предел суммы n первых ее членов при .

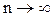Найти эту сумму можно по следующей формуле:


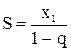
Числовую последовательность {bn}, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же число q ≠ 0, называют геометрической прогрессией:


bn + 1 = bn · q.

Важно отметить, что число q, которое называется знаменателем прогрессии, отлично от нуля. Так как 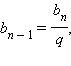  то 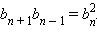 Верна и обратная теорема.

Последовательность {bn} является геометрической тогда и только тогда, когда для любого n > 1 выполняется соотношение

где 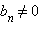при всех n. Тем не менее, важно понимать, что формула 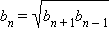справедлива только для геометрической прогрессии с положительными членами, а предыдущее соотношение верно для произвольной геометрической прогрессии.

Каждый член геометрической прогрессии {bn} определяется формулой

bn = b1 · qn – 1.



2. Процесс стандартизации параметрических рядов с помощью геометрической прогрессии


Процесс стандартизации параметрических рядов - параметрическая стандартизация - заключается в выборе и обосновании целесообразной номенклатуры и численного значения параметров. Решается эта задача с помощью математических методов.

При создании, например, размерных рядов одежды и обуви производятся антропометрические измерения большого числа мужчин и женщин разных возрастов, проживающих в различных районах страны. Полученные данные обрабатывают методами математической статистики.

Параметрические ряды машин, приборов, тары рекомендуется строить согласно системе предпочтительных чисел - набору последовательных чисел, изменяющихся в геометрической прогрессии.

Смысл этой системы заключается в выборе лишь тех значений параметров, которые подчиняются строго определенной математической закономерности, а не любых значений, принимаемых в результате расчетов или в порядке волевого решения.

Основным стандартом в этой области является ГОСТ 8032 «Предпочтительные числа и ряды предпочтительных чисел». На базе этого стандарта утвержден ГОСТ 6636 «Нормальные линейные размеры», устанавливающий ряды чисел для выбора линейных размеров.

ГОСТ 8032 предусматривает четыре основных ряда предпочтительных чисел:

1-й ряд - R5 - 1,00; 1,60; 2,50; 4,00; 6,30; 10,00... имеет знаменатель прогрессии ;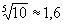

2-й ряд – R10 - 1,00; 1,25; 1,60; 2,00; 2,50 ...

имеет знаменатель ;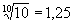

3-й ряд - R20 - 1,00; 1,12; 1,25; 1,40; 1,60 …

имеет знаменатель ;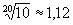

4-й ряд - R40 - 1,00; l,06; 1,12; 1,18; 1,25 ...

имеет знаменатель ;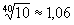

Количество чисел в интервале 1 — 10: для ряда R5 — 5, R10 - 10, R20 - 20, для ряда R40 - 40.

В некоторых технически обоснованных случаях допускается округление предпочтительных чисел. Например, число 1,06 может быть округлено до 1,05; 1,12 - до 1,1; 1,18 - до 1,15 или 1,20.

При выборе того или иного ряда учитывают интересы не только потребителей продукции, но и изготовителей. Частота параметрического ряда должна быть оптимальной: слишком «густой» ряд позволяет максимально удовлетворить нужды потребителей (предприятий, индивидуальных покупателей), но, с другой стороны, чрезмерно расширяется номенклатура продукции, распыляется ее производство, что приводит к большим производственным затратам. Поэтому ряд R5 является более предпочтительным по сравнению с рядом R10, а ряд R10 предпочтительнее ряда R20.

Применение системы предпочтительных чисел позволяет не только унифицировать параметры продукции определенного типа, но и увязать по параметрам продукцию различных видов - детали, изделия, транспортные средства и технологическое оборудование.

Например, практика стандартизации в машиностроении показала, что параметрические ряды деталей и узлов должны базироваться на параметрических рядах машин и оборудования. При этом целесообразно руководствоваться следующим правилом: ряду параметров машин по R5 должен соответствовать ряд размеров деталей по R10, ряду параметров машин по R10 - ряд размеров деталей по R20 и т.д.

В целях более эффективного использования тары для консервных банок и транспортных средств для их перевозки предлагается ряд грузоподъемности железнодорожных вагонов и автомашин, ряд размеров контейнеров, ящиков и отдельных консервных банок строить по ряду R5[1].

3. Реформирование стандартизации по информационным технологиям


Наша планета, в общем-то незаметно и относительно безболезненно, «вкатилась» в III тысячелетие от Рождества Христова. Все-таки хоть и маленький, но юбилей! Так сказать: «Есть повод подвести итоги и наметить перспективы». При всей условности этой даты даже вблизи отчетливо виден водораздел двух эпох. На глазах исчезает поляризация мира по оси «Запад – Восток» и появляется новая – «Север – Юг». Невразумительное по названию постиндустриальное общество незаметно трансформировалось в информационное. Распалась великая советская империя и появляется новая – Единая Европа. Новые времена, новые задачи или, как любят говорить на Западе, «новые вызовы».

Попытаемся определить или хотя бы предположить - каким должен быть инженер в этом новом тысячелетии, и сравним с тем, что предлагает сегодня российская высшая инженерная школа.

Кто-то из великих изрек достаточно тривиальный, но не ставший от этого ложным, афоризм: «Понять будущее можно только опираясь на знание прошедшего». Вот и мы в начале проследим эволюцию инженера в современном ему мире. Оставим в покое анонимных изобретателей клина, колеса и пороха, а так же Архимеда, Аристотеля, Леонардо да Винчи и тысячи других гениальных инженеров-одиночек.

Как массовая профессия, инженер появился во второй половине XIX века и сформировался к концу того же века.

И в то время это был настоящий Инженер.

В российской литературе, а затем и в кино сформировался стереотип такого инженера: сначала - студент в форменном кителе, ведущий уважительный, но равноправный спор с маститым седовласым профессором (лучше всего с бородой как у Жуковского или Менделеева) в стенах петербургского технологического института или московского императорского технического училища.

А затем - инженер непременно в пенсне или очках, в форменной фуражке с молоточками, стоящий в лодке под мостом, который он спроектировал и построил, и по которому сейчас пройдет первый поезд.

Такой инженер, по крайней мере - до революции, был хорошо обеспечен, жил в большой квартире, имел прислугу, отдыхал за границей или на худой конец - в Крыму.

При всей условности, такой образ, тем не менее, достаточно точно отражал место инженера в России конца XIX начала XX века.

И действительно, накопленные к тому времени инженерные знания еще позволяли за пять лет обучения и за 3–4 года практики получить весь необходимый объем информации и навыков для успешной работы в широких областях (механика, теплотехника, электромеханика и др.) производства.

Проектирование и изготовление технических устройств того времени (мост, паровоз, орудие и даже корабль) еще можно было «удержать в голове» одного человека и зачастую такие устройства имели одного «автора».

Дефицит инженерных кадров и относительно малые затраты «инженеро-часов» при проектировании и изготовлении обеспечивали очень высокий уровень оплаты инженерного труда.

Инженерное образование того периода в целом соответствовало требованиям по подготовке инженеров.

Достаточный объем фундаментальных наук, и известные к тому времени знания по материаловедению, сопромату и теории машин и механизмов и технологии металлообработки (если рассматривать пример специальности инженер-механик) «умещались» в учебный план четырех - четырех с половиной лет.

Оставшееся время посвящалось выполнению квалификационной работы – дипломному проекту, который в то время практически не отличался от реальных проектов промышленности.

Но «золотой век» инженеров длился не долго. Технические системы усложнялись в геометрической прогрессии, новые проекты разрабатывались все более разрастающимися коллективами все более «сужающихся» специалистов.

Очень быстро росло число инженерных специальностей, внутри каждой специальности произошло разделение на проектировщиков, технологов и эксплуатационников. Первый самолет братья Райт создали вдвоем, а уже через 40 лет в создании самолета B-29 на фирме Боинг принимало участие более 400 человек только инженеров–проектировщиков. Работа таких больших коллективов потребовала появления еще одной специализации «инженеры-управленцы».

С этого времени инженерное образование во всем мире начинает все больше отставать от быстро меняющихся требований промышленности, со все большим временным запаздыванием начинается подготовка инженеров по новым специальностям, учебные программы по старинке ориентируются только на подготовку инженеров-проектировщиков, не смотря на перегрузку учебных планов, все более увеличивается отставание учебных курсов от последних достижений технического прогресса.

У нас в стране этот процесс усугублялся социальными катаклизмами начала XX века. Многие выдающиеся инженеры и преподаватели эмигрировали или погибли во время революции и гражданской войны. В ходе индустриализации, когда зачастую при подготовке инженеров большее внимание уделялось не знанию технических предметов, а социальному происхождению и классовому чутью, упор был сделан на количественный показатель.

В стране ударными темпами создавались новые технические ВУЗы, открывались новые специальности.

Принцип подготовки инженеров «пусть поплоше, но побольше!» был доведен у нас в стране до абсурда к 80-м годам XX века. В это время появились должности «инженер по соцсоревнованию», на предприятиях висели объявления «требуется инженер, умеющий печатать на машинке». При общей нищете советского общества, бедность инженеров была постоянной темой анекдотов.

А советское высшее техническое образование продолжало во все возрастающих количествах «штамповать» инженеров-проектировщиков уровень подготовки которых для 90% «инженерных» вакансий был избыточен, а для 10% действительно инженерных должностей совершенно недостаточен. Вместо целенаправленной подготовке инженеров-упрвленцев использовался суррогат «Комсомольско-профсоюзно-партийной» работы[2].

Во все времена делались всевозможные предсказания «смертности» общества, «конца света» и иные малоприятные для человечества прогнозы. Однако употребление нами термина «время жизни» определяется естественнонаучным подходом, а не традицией «роковых» предсказаний.

Время жизни разных по качеству жизни типов обществ - вот что подразумевает приведенная выкладка.

Из нее следует только то, с какой скоростью один тип социальной жизни по его качеству и организации заменяется другим. Результаты этого анализа свидетельствуют о процессе ускорения социальной эволюции по мере увеличения энергетической мощи общества[3].

Чем более емкие и мощные источники энергии появляются в руках людей, тем быстрее и легче они реализуют всегда в избытке витающие в обществе технологические идеи.

По существу, речь идет о давно известном в общественных науках положении, сформулированном классиком психологии и социологии, французским исследователем Г.Лебоном следующим образом: «...Действующая в продолжении известного времени в одном направлении какая-нибудь причина быстро производит очень большие результаты. ...Когда эта причина продолжает производить одно и то же следствие, то причины растут в арифметической прогрессии (1, 2, 3, 4, 5...), а следствия - в геометрической прогрессии (2, 4, 8, 16, 32...). /.../ Этими соображениями объясняется тот факт, что большинство социальных явлений может быть выражено быстро возрастающими геометрическими кривыми»[4].

     Творчество Г.Лебона имеет уже столетнюю историю. Но и за сто лет до него исследователи опирались на данную закономерность. Наиболее характерен здесь пример выдающегося демографа и экономиста Т.Мальтуса, который, изучая физическое воспроизводства человека в период индустриальной (и одновременно демографической) революции, выявил следующую закономерность: «...Средства существования при наиболее благоприятных условиях применения человеческого труда никогда не могут возрастать быстрее, чем в арифметической прогрессии. ...если возрастание населения не задерживается какими-либо препятствиями, то это население удваивается через каждые 25 лет и, следовательно, возрастает в каждый последующий двадцатипятилетний период в геометрической прогрессии»[5].

Заключение


Геометрическая прогрессия играет большую и важную роль не только  в школьном курсе алгебры, но и в дальнейшем обучении в высших учебных заведениях.

Важность этого на первый взгляд небольшого раздела школьного курса заключается в его чрезвычайно широких областях применения, в частности он часто применяется в теории рядов, рассматриваемой на II-III курсах университета.

Итак, геометрическая прогрессия - числовая последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предшествующему члену, умноженному на одно и тоже не равное нулю число, называется геометрической прогрессией.

Если общая закономерность верна, то можно утверждать, что на возрастание в геометрической прогрессии своей энергетической мощи общество реагирует геометрическим ростом различного рода социальных последствий. В этом, с одной стороны, лежит причина ускорения исторического процесса, однако с другой стороны, скрывается и возможный рост различного рода социальных девиаций и патологий.



Список литературы



1.     Антонюк Д.И. Основы стандартизации. М.: Издательство «НОРМА», 2003.

2.     Быков В.П.  Прогнозы человечества // Инженерное образование, № 2, 2003.

3.     Горохов С.С. Мальтус Т.Р. Биография. Изложение сути работ. М.: Просвещение, 1981.

4.     Домников А.С. Инженерная эволюция // Инженерное образование, № 3, 2004.

5.     Пушница Е.С. Г. Лебон Афоризмы, мысли, фразы. М.: Мысль, 1988.




[1] Антонюк Д.И. Основы стандартизации. М.: Издательство «НОРМА», 2003. С. 108.

[2] Домников А.С. Инженерная эволюция // Инженерное образование, № 3, 2004. С. 5.

[3] Быков В.П.  Прогнозы человечества // Инженерное образование, № 2, 2003. С. 4.

[4] См.: Пушница Е.С. Г. Лебон Афоризмы, мысли, фразы. М.: Мысль, 1988. С. 127.

[5] См.: Горохов С.С. Мальтус Т.Р. Биография. Изложение сути работ. М.: Просвещение, 1981. С. 12-14.