ЗАДАНИЕ

Федеральное агентство по образованию

Всероссийский заочный финансово-экономический институт

Отчет

по лабораторной работе по дисциплине «Эконометрика»

вариант №3

Исполнитель: Солдатова Т.С.

Специальность: БУАиА

Группа: дневная, 1

Руководитель: О.В.Прокофьев

Пенза 2008г.

ЗАДАНИЕ

По данным представленным в таблице 1 , изучается зависимость индекса человеческого развития[1] от переменных:

х₁ – ВВП 1997 г., % к 1990 г.;

х₂ – расходы на конечное потребление в текущих ценах, % к ВВП;

х₃ – расходы домашних хозяйств, % к ВВП;

х₄ – валовое накопление, % к ВВП;

х₅ – суточная калорийность питания населения, ккал на душу населения;

х₆ – ожидаемая продолжительность жизни при рождении в 1997 г., число лет.

страна	у	х1	х2	х3	х4	х5	х6
Австрия	0,904	115	75,5	56,1	25,2	3343	77
Австралия	0,922	123	78,5	61,8	21,8	3001	78,2
Белоруссия	0,763	74	78,4	59,1	25,7	3101	68
Бельгия	0,923	111	77,7	63,3	17,8	3543	77,2
Великобритания	0,918	113	84,4	64,1	15,9	3237	77,2
Германия	0,906	110	75,9	57	22,4	3330	77,2
Дания	0,905	119	76	50,7	20,6	3808	75,7
Индия	0,545	146	67,5	57,1	25,2	2415	62,6
Испания	0,894	113	78,2	62	20,7	3295	78
Италия	0,9	108	78,1	61,8	17,5	3504	78,2
Канада	0,932	113	78,6	58,6	19,7	3056	79
Казахстан	0,74	71	84	71,7	18,5	3007	67,6
Китай	0,701	210	59,2	48	42,4	2844	69,8
Латвия	0,744	94	90,2	63,9	23	2861	68,4
Нидерланды	0,921	118	72,8	59,1	20,2	3259	77,9
Норвегия	0,927	130	67,7	47,5	25,2	3350	78,1
Польша	0,802	127	82,6	65,3	22,4	3344	72,5
Россия	0,747	61	74,4	53,2	22,7	2704	66,6
США	0,927	117	83,3	67,9	18,1	3642	76,7
Украина	0,721	46	83,7	61,7	20,1	2753	68,8
Финляндия	0,913	107	73,8	52,9	17,3	2916	76,8
Франция	0,918	110	79,2	59,9	16,8	3551	78,1
Чехия	0,833	99,2	71,5	51,5	29,9	3177	73,9
Швейцария	0,914	101	75,3	61,2	20,3	3280	78,6
Швеция	0,923	105	79	53,1	14,1	3160	78,5

Задание

1. Постройте матрицу парных коэффициентов корреляции. Установите, какие факторы мультиколлинеарны.

2. Постройте уравнение множественной регрессии в линейной форме с полным набором факторов.

3. Оцените статистическую значимость уравнения регрессии и его параметров с помощью критериев Фишера и Стьюдента.

4. Отберите информативные факторы по п. 1 и 3. Постройте уравнение регрессии со статистически значимыми факторами.

5. Проверьте выполнение предпосылок МНК, в том числе проведите тестирование ошибок уравнения множественной регрессии на гетероскедастичность.

Вводим таблицу данных. В этом примере n=25, m=6.

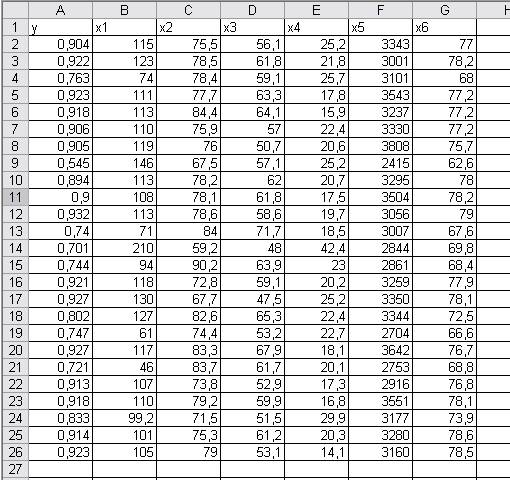
Рис. 1. Таблица исходных данных

Используем инструмент Корреляция

Для проведения корреляционного анализа выполним следующие действия:

1. Данные для корреляционного анализа должны располагаться в смежных диапазонах ячеек.

2. Выберем команду Сервис→Анализ данных.

3. В диалоговом окне Анализ данных выберете инструмент Корреляция, а затем щелкните ОК.

4. В диалоговом окне Корреляция в поле Входной интервал вводим B1;H26. Так как у нас выделены заголовки столбцов, то установим флажок Метки в первой строке.

5. Выберем параметры вывода.

6. ОК.

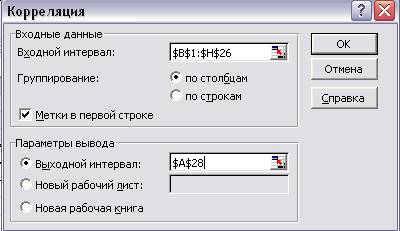
Рис 2. Диалоговое окно Корреляция.

Получим матрицу коэффициентов парной корреляции.

Рис. 3. Матрица коэффициентов парной корреляции.

Анализ матрицы коэффициентов парной корреляции показывает, что зависимая переменная, т.е. индекс человеческого развития, имеет тесную связь с суточной калорийностью питания населения (ryx₅ = 0,751) и с ожидаемой продолжительностью жизни при рождении в 1997 г. (ryx₆ = 0,962). Факторы х₅ и х₆ не мультиколлинеарны, так как соблюдается правило неравенств:

0,751>0,704

0,962>0,704

0,704<0,8

Следует, что включаем в модель факторы х₅ и х₆.

Для проведения регрессионного анализа выполним следующие действия:

1. Выберем команду Сервис → Анализ данных.

2. В диалоговом окне Анализ данных выберем инструмент Регрессия, затем щелкнем на кнопке ОК.

3. В диалоговом окне Регрессия в поле Входной интервал Y введем А1:А26, который представляет зависимую переменную. В поле Входной интервал Х введем В1:G26, который содержит значения независимых переменных (рис 4).

4. Установим флажок Метки в первой строке, так как мы выделим заголовки столбцов.

5. Выберем параметры ввода.

6. В поле остатки поставим флажок на остатки и график остатков.

7. ОК.

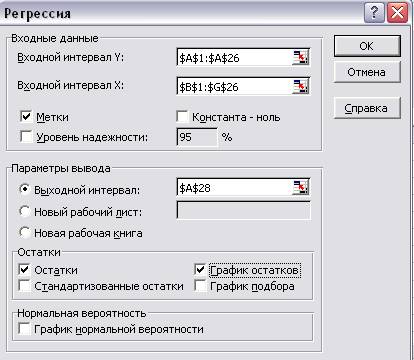
Рис.4. Диалоговое окно Регрессия.

Получим отчет по регрессионному и дисперсионному анализу (рис.5).

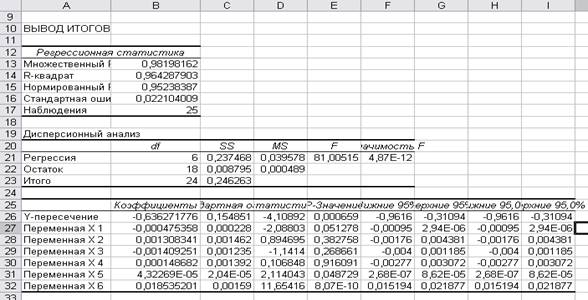
Рис. 5. Вывод итогов регрессионного анализа.

Для построения уравнения множественной регрессии в линейной форме воспользуемся коэффициентами из диапазона В26:В32.

Получим уравнение:

y = -0,636272 - 0,000475x₁ + 0,001308x₂ – 0,001409x₃ + 0,000148x₄ + 4,32269E-05x₅ + 0,018535x₆

На рис.5 приведены вычисленные (предсказанные) по модели значения зависимой переменной Y и значения остаточной компоненты e_i.

Значение коэффициента детерминации и множественной корреляции можно найти в таблице Регрессионная статистика на рис.5. Коэффициент детерминации равен 0,964. он показывает долю вариации результативного признака под воздействием изучаемых факторов. Следовательно, 96,4% вариации зависимой переменной учтено в модели и обусловлено влиянием включенных факторов.

Коэффициент множественной корреляции R равен 0,982 он показывает сильную тесноту связи зависимой переменной Y с независимыми факторами Х.

Следовательно, можно сказать, что модель уравнения регрессии хорошего качества.

Оценим качество параметров уравнения регрессии с помощью t-критерия Стьюдента.

Введем в пустую ячейку табличное значение коэффициента Стьюдента (рис. 6):

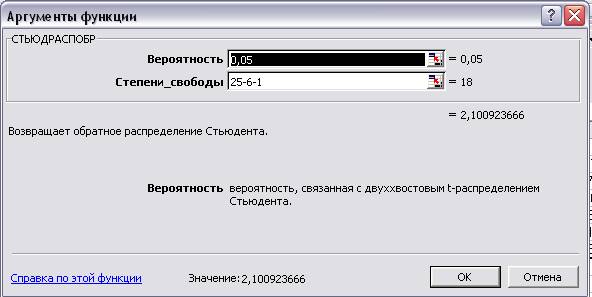
Рис.6. Аргументы функции.

Получим значение равное 2,1009

Сравним это значение с ячейками D2:D32. Отсюда следует, так как |t_расч|>t_табл , то коэффициенты а₀, а₁, а₅ и а₆ существенны (значимы).

Оценим качество параметров уравнения регрессии с помощью F-критерия Фишера. Значение F-критерия Фишера можно найти в таблице Регрессионная статистика рис.5., оно равно 81,005.

Табличное значение F-критерия при доверительной вероятности 0,05 при v₁=5 и v₂=25-6=11 составляет 2,7400, который вычисляется по формуле:

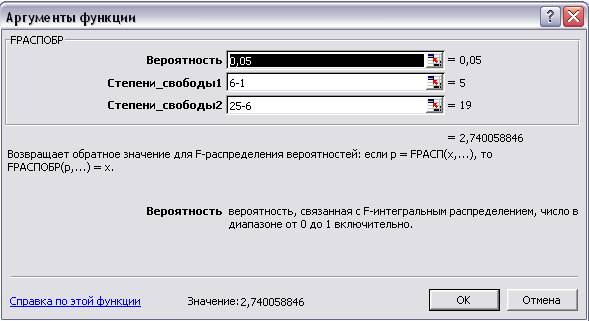
Рис.7. Аргументы функции

Поскольку F_расч>F_табл,(81,005>2,7400)уравнение регрессии следует признать адекватным.

Из пунктов 1-3 нам нужно отобрать статистически значимые факторы. Из пункта 1 мы отобрали факторы х₅ и х₆. Теперь определим значимы ли эти коэффициенты с помощью t-статистики. Для этого введем с помощью автозаполнителя формулы для расчета наблюдаемой t-статистики (начиная с ячейки А38) и с помощью мастера функций – табличное значение t-статистики (ячейка А45) (рис.8).

Рис.8. Расчет t-статистики

Получим значения (рис.9):

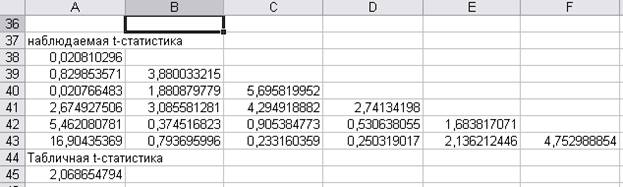
Рис 9. Полученные значения t-статистики

Сравнивая расчетные и табличное значения, определим, так как t_набл>t_табл коэффициенты х₅ и х_6,которые мы отобрали в пункте 1 статистически значимы.

Скопируем выбранные данные на отдельный лист.

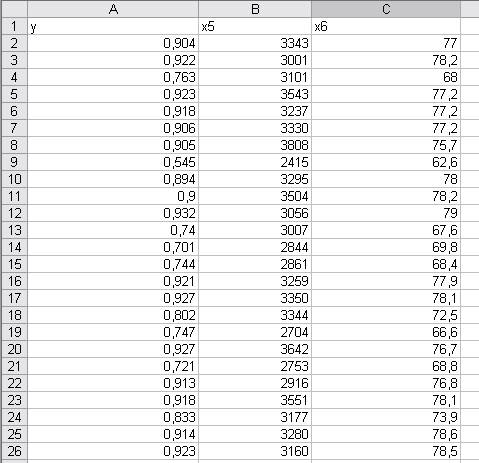
Рис.10. Выбранные данные.

Вызовем окно Сервис, Анализ данных, Регрессия. Заполним его

Рис. 11. Диалоговое окно Регрессия

Получим отчет по регрессионному и дисперсионному анализу (рис.12.), (рис.13.)

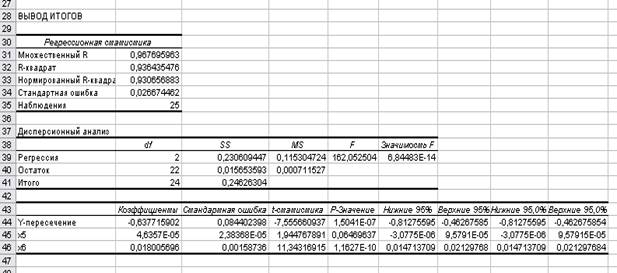
Рис. 12. Вывод итогов

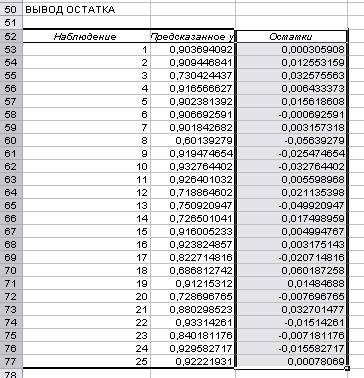
Рис 13. Вывод остатка

Оценим качество модели, сравним ячейку (В32) из таблицы вывода итогов рис.12., т.е. R-квадрат равен 0,9364, что говорит о высоком качестве модели.

Введем в любую пустую ячейку табличное значение коэффициента Стьюдента (рис.14)

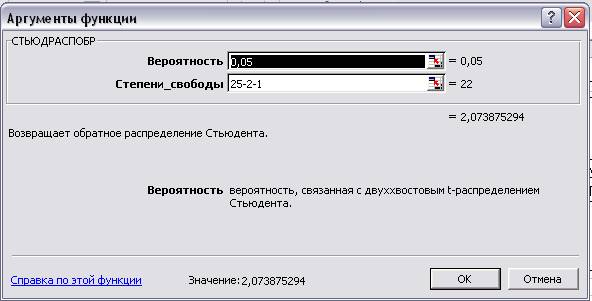
Рис. 14. Аргументы функции

Сравним по модулю с t-статистикой из таблицы вывода итогов рис. 12. Отсюда мы видим, что все коэффициенты статистически значимы, х₅тоже можно считать значимым коэффициентом корреляции, так как отклонение незначительно.

Введем в любую пустую ячейку табличное значение критерия Фишера (рис.15)

Рис. 15. Аргументы функции

Сравним это значение со значением из таблицы вывод итогов в ячейке регрессия: F. Так как F_расч>F_табл(162,05>3,44), значит уравнение регрессии следует признать адекватным.

Построим уравнение регрессии со статистически значимыми факторами:

Y=-0,637716+4,6357E-05x₁+0,018006x₂

Предпосылка 1. Проверка случайного характера остатков.

Построим график е (ŷ). Для этого используйте мастер диаграмм и данные Предсказанное Y, Остатки (рис.16).

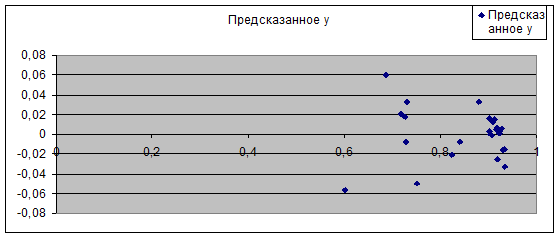
Рис. 16. График е (ŷ).

На этом графике видно, остатки расположены случайным образом внутри горизонтальной полосы, следовательно, можно сделать вывод о том, что величины случайны. Первая предпосылка МНК выполняется.

Предпосылка 2. Нулевая гипотеза остатков.

Построим графики е (х5), е (х6). Для этого возьмем Графики остатков из окна Регрессия (рис17. и рис.18).

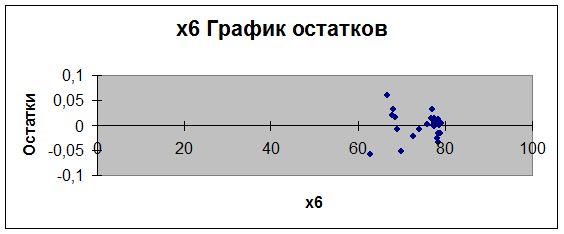
Рис.17 график остатков е (х5)

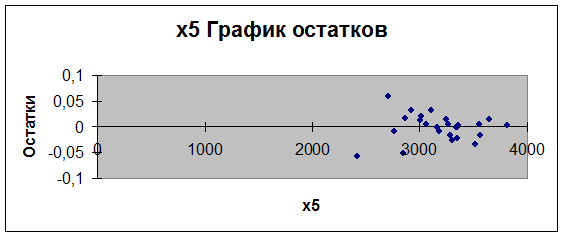
Рис.18. график остатков е (х6)

Мы видим, что на графиках остатки расположены в виде горизонтальной полосы, следовательно, они не зависимы от значений Х. Отсюда, делаем вывод, что вторая предпосылка МНК выполняется.

Предпосылка 3. Гетероскедастичность – это, когда для каждого значения факторов остатки имеют различную дисперсию.

Проверим предпосылку с помощью критерия Гольдфельда –Кванта. Используется для проверки гомоскедастичности. Критерий обоснован для линейной модели, в которой дисперсия остатков пропорциональна квадрату факторов.

Скопируем исходные данные Y, X5, X6 на отдельный рабочий лист.

Получим исходные данные (рис.19).

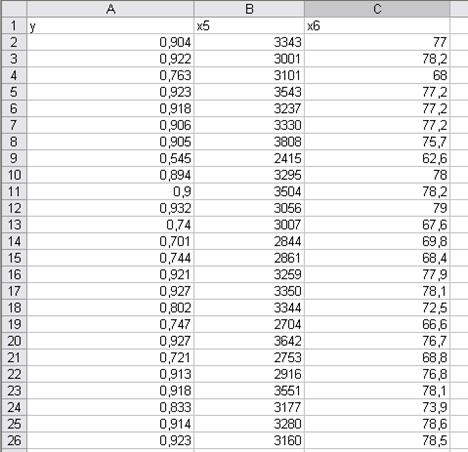
Рис. 19.Выбранные данные.

Проверим дисперсию остатков на наличие гетероскедастичности по фактору Х5.

Выделим там все ячейки, вызовем окно Данные, Сортировка (рис.20)

Рис. 20. Сортировка диапазона

Получим список, отсортированный по Х5 (рис.21).

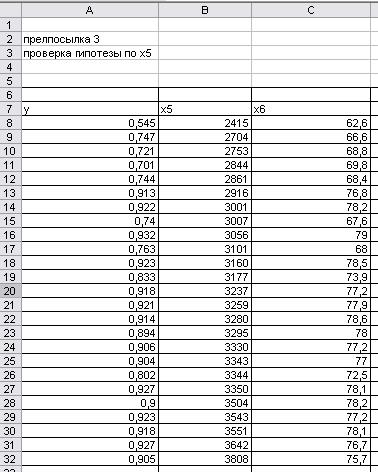
Рис. 21. Отсортированные данные по Х5

Разобьем данные на 2 группы, между которыми – исключаемые центральные наблюдения, мы исключили 5 значений (рис.22).

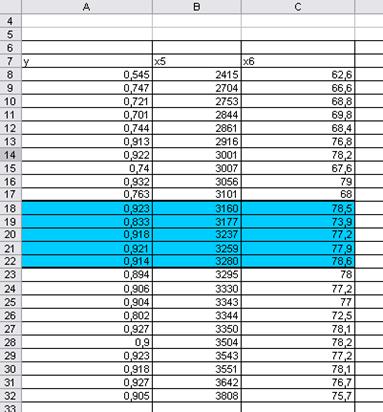
Рис.22 Исключение данных

Найдем суммы квадратов остатков для каждой группы. Для каждой половины построен отчет по регрессии (Сервис, Анализ данных, Регрессия). Ячейка, где находится сумма квадратов остатков, выделим желтым цветом (рис.23, рис.24, рис.25 и рис.26).

Рис.23. Диалоговое окно Регрессия

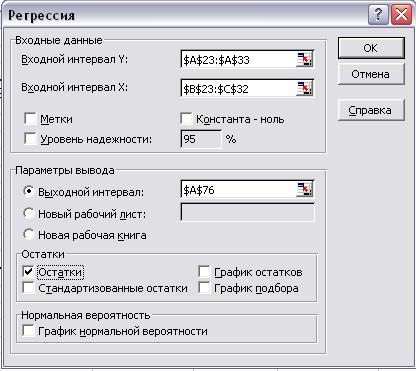
Рис. 24. Диалоговое окно Регрессия

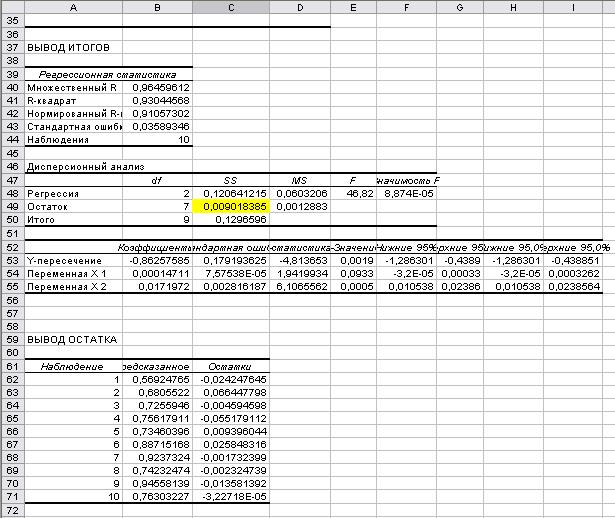
Рис.25. Вывод итогов

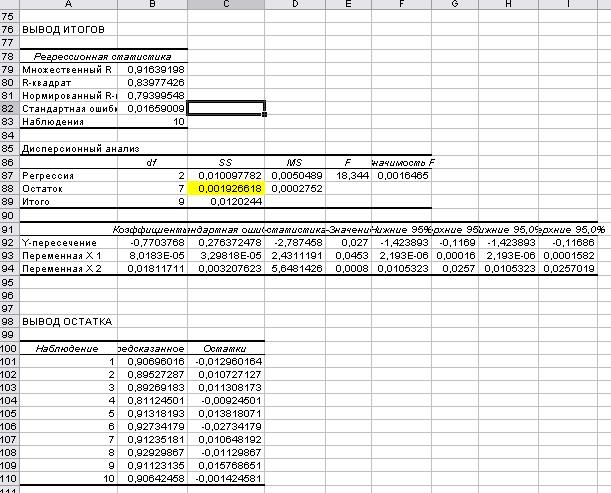
Рис. 26. Вывод итогов.

В любую пустую ячейку введем критерий Гольдфельда-Квандта как частное. Надо большую сумму квадратов остатков разделить на меньшую (рис.27).

Рис. 27. Формула расчета критерия Гольдфельда-Квандта

Получим значение 4,6809.

В любую пустую ячейку введем табличный F-критерий (рис.28):

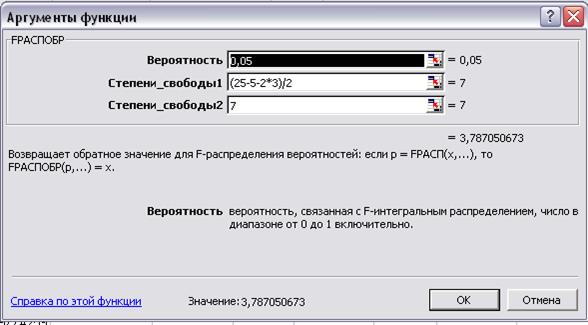
Рис. 28. Аргументы функции

Сравним значение F_расч с F_табл, так как F_расч > F_табл (4,6809>3,7871), значит присутствует гетероскедастичность.

Проверим дисперсию остатков на наличие гетероскедастичности по фактору Х6.

Выделим там все ячейки, вызовем окно Данные, Сортировка (рис.29).

Рис. 29. Сортировка диапазона

Получим список, отсортированный по Х6 (рис.30).

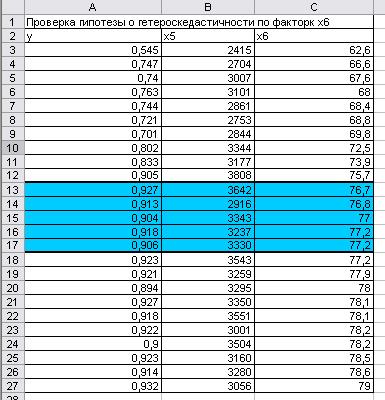
Рис. 30. Отсортированные данные по Х6

Рис. 31. Диалоговое окно Регрессия

Рис. 32. Диалоговое окно Регрессия

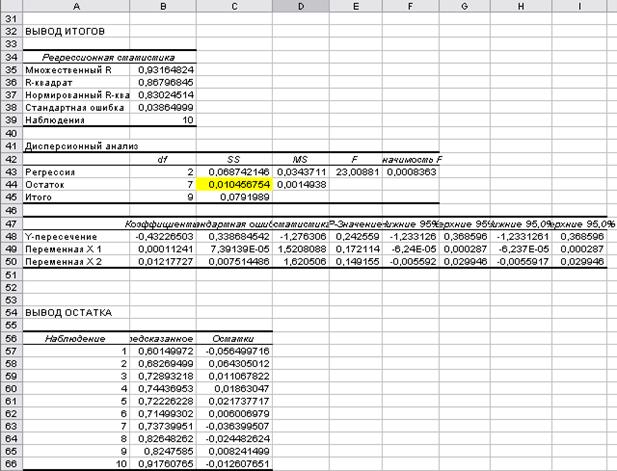
Рис. 33. Вывод итогов

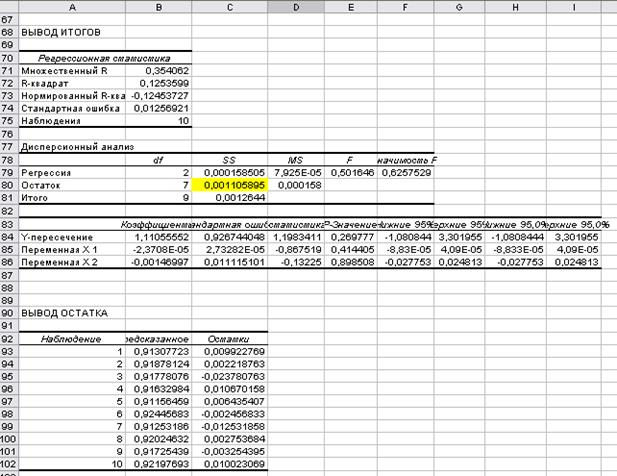
Рис.34. Вывод итогов

В любую пустую ячейку введем критерий Гольдфельда-Квандта как частное. Надо большую сумму квадратов остатков разделить на меньшую (рис.35).

Рис. 35. Формула расчета критерия Гольдфельда-Квандта

Получим значение 9,4555.

В любую пустую ячейку введем табличный F-критерий (рис.36):

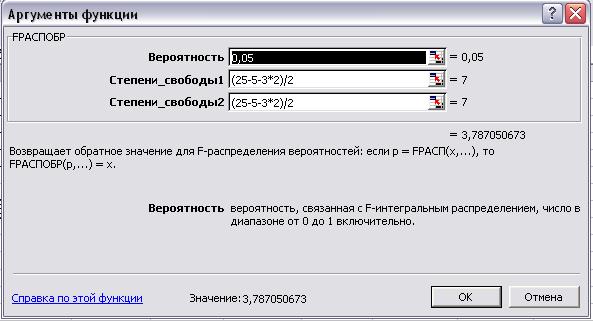
Рис. 36. Аргументы функции

Сравним значение F_расч с F_табл, так как F_расч > F_табл (9,4555>3,7871), значит присутствует гетероскедастичность. Следовательно третья предпосылка не выполняется.

Предпосылка 4. О независимости остатков. Остатки должны быть распределены независимо друг от друга.

Остатки регрессионной модели Y(X5, X6) из ячеек С52:С77 (рис. 13) скопируем в новый лист.

Добавим формулы разности и произведения соседних значений остатков, суммы по столбцам (рис.37).

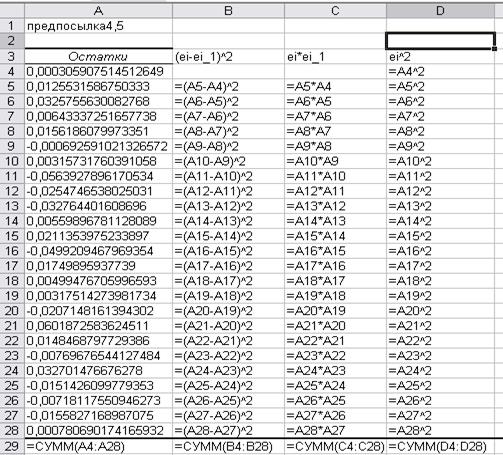
Рис. 37. Формулы разности и произведения соседних значений остатков

Получим значения (рис.38).

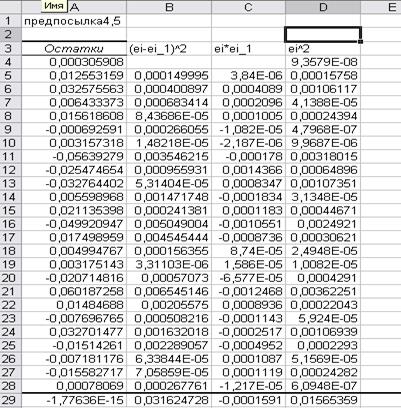
Рис. 38. Рассчитанные значения остатков

Рассчитаем коэффициент Дарбана-Уотсона по формуле при критических значениях1,21 и 1,55 (рис.39):

Рис. 39. Формула расчета коэффициента Дарбана-Уотсона

Получим значение равное 1,9797. Так как значение попадает в интервал от 1,55 до 2,следовательно, остатки независимы и предпосылка выполняется.

Предпосылка 5. О нормальном законе распределения остатков

R/S – критерий.

Рассчитаем его по формуле при критических значениях 3,34 и 4,57 (рис.40):

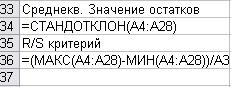
Рис. 40. Формулы расчета R/S – критерия

Получим значение равное 4,5648. Так как значение попадает в интервал между критическими значениями, значит, остатки подчиняются нормальному закону распределения и предпосылка выполняется.

Вывод

Не все предпосылки выполняются, модель нуждается в совершенствовании.

[1] Специальный индекс человеческого развития, который объединяет три показателя (валовой внутренний продукт на душу населения, грамотность и продолжительность предстоящей жизни) и дает обобщенную оценку человеческого прогресса.