Профессиональное выполнение дипломных, курсовых работ, рефератов- writer5.ru !

Министерство образования Российской Федерации

Всероссийский заочный финансово-экономический институт

Филиал г.Барнаула

Студентки: 4 курса группы

Специальность: Финансы и кредиты

Номер личного дела:

Образование: первое высшее

Вариант: 3

Проверила: Поддубная М.Л.

Г.Барнаул – 2006г.

Задание 1

В каждом варианте приведены поквартальные данные о кредитах от коммерческого банка на жилищное строительство (в условных единицах) за 4 года (всего 16 кварталов, первая строка соответствует первому кварталу первого года).

Требуется:

1. Построить адаптивную мультипликативную модель Хольта-Уинтерса с учетом сезонного фактора, приняв параметры сглаживания a(a)=0,3; a(b)=0,3; a(F)=0,6.

2. Оценить точность построенной модели с использованием средней относительной ошибки аппроксимации.

3. Оценить адекватность построенной модели на основе исследования:

- случайности остаточной компоненты по критерию пиков;

- независимости уровней ряда остатков по d-критерию (критические значения d1=1,10 и d2=1,37) и по первому коэффициенту автокорреляции при критическом значении r кр =0,32.

- нормальности распределения остаточной компоненты по R/S-критерию с критическими значениями от 3 до 4,21.

4. Построить точечный прогноз на 4 шага вперед, т.е. на 1 год.

5. Отразить на графике фактические, расчетные и прогнозные данные.

Исходные данные:

Таблица 1

Квартал		Квартал
1	31	12	35
2	40	13	42
3	47	14	52
4	31	15	62
5	34	16	39
6	44
7	54
8	33
9	37
10	48
11	57

Решение

Подготовим расчетную таблицу, в которой включим столбцы t, Y, , , , .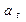

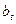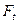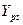Таблица 2

t
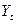
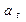
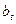
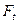
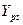
-3				0,86
-2				1,08
-1				1,27
0		35,07	0,93	0,79
1	31
2	40
3	47
4	31
5	34
6	44
7	54
8	33
9	37
10	48
11	57
12	35
13	42
14	52
15	62
16	39
17
18
19
20

Для заполнения Таблицы2 выполним предварительный расчет.

Для определения трендовых коэффициентов построим вспомогательную линейную регрессию по данным за первые восемь кварталов (2 года).

Воспользуемся средствами табличного процессора Microsoft Excel (Сервис/Анализ данных/Регрессия) и получим следующие данные:

Таблица3

	Коэффициенты
Y-пересечение	35,07
Переменная X 1	0,93

Таким образом, мы нашли значения а(0)=35,07 и b(0)=0,93.

Рассчитаем значения коэффициентов сезонности I-IV кварталов F(-3), F(-2), F(-1) и F(0) для года, предшествующего первому году.

Воспользуемся построенной регрессией (Таблица 4 – столбец предсказанное Y) для расчета коэффициента сезонности.

Таблица4

Наблюдение	Предсказанное Y	Остатки
1	36,00	-5,00
2	36,93	3,07
3	37,86	9,14
4	38,79	-7,79
5	39,71	-5,71
6	40,64	3,36
7	41,57	12,43
8	42,50	-9,50

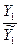- коэффициент сезонности 1 квартала 1 года

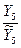- коэффициент сезонности 1 квартала 2 года

В качестве оценки коэффициента сезонности 1 квартала предыдущего года возьмем среднее арифметическое:

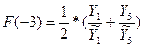
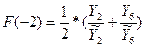
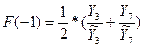
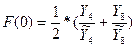
и получим

F(-3)=0,86; F(-2)=1,08; F(-1)=1,27; F(0)=0,79

Оценив значения a(0), b(0) , а также F(-3), F(-2), F(-1) и F(0), перейдем к построению адаптивной мультипликативной модели Хольта-Уинтерса с помощью формул:

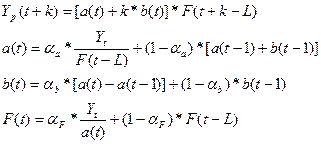
Рассчитаем значения 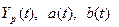и .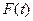

Выберем t=0, k=1 => =>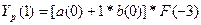

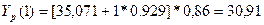
Уточним коэффициенты модели: примем t=1 и вычислим

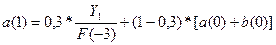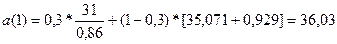
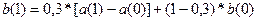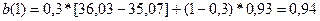
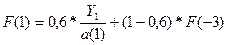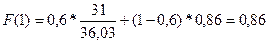
Аналогично определяются остальные коэффициенты и для всех уровней исходных данных (т.е. за 16 кварталов).

Полученная таблица называется моделью Хольта-Уинтерса.

Таблица 5

t	Y(t)	a(t)	b(t)	F(t)	Yp(t)
-3				0,86
-2				1,08
-1				1,27
0		35,07	0,93	0,79
1	31	36,03	0,94	0,86	30,91
2	40	36,96	0,94	1,08	40,03
3	47	37,63	0,85	1,26	48,14
4	31	38,74	0,93	0,80	30,32
5	34	39,64	0,92	0,86	34,11
6	44	40,58	0,93	1,08	43,90
7	54	41,94	1,06	1,28	52,21
8	33	42,55	0,92	0,78	34,20
9	37	43,36	0,89	0,86	37,32
10	48	44,26	0,89	1,08	47,94
11	57	45,02	0,85	1,27	57,60
12	35	45,51	0,74	0,77	35,94
13	42	47,11	1,00	0,88	39,57
14	52	48,07	0,99	1,08	52,15
15	62	48,98	0,97	1,27	62,29
16	39	50,07	1,00	0,78	38,70
17					44,79
18					56,38
19					67,26
20					42,03

2. Оценить точность построенной модели с использованием средней относительной ошибки аппроксимации.

По столбцам исходных данных (Таблица 2) и полученных данных 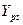(Таблица 4) рассчитаем остатки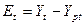

Получим следующие результаты

Таблица6

*E(t)*	*отн.погр.*	*E(t)*	*отн.погр.*
0,09	0,29	-0,94	2,67
-0,03	0,08	2,43	5,79
-1,14	2,42	-0,15	0,29
0,68	2,20	-0,29	0,47
-0,11	0,31	0,30	0,76
0,10	0,22
1,79	3,32
-1,20	3,62
-0,32	0,87
0,06	0,12
-0,60	1,05

Для проверки точности рассчитаем относительную погрешность каждого уровня

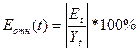
используя функции табличного процессора Microsoft Excel (Мастер функции/Категория – Математические/ABS) (Таблица 6).

По полученным результатам определим среднее значение с помощью функций табличного процессора Microsoft Excel (Мастер функции/Категория – Статистические/СРЗНАЧ).

Средняя относительная ошибка аппроксимации составляет 1,53%, которая меньше 5% => модель имеет высокую точность.

3. Оценить адекватность построенной модели на основе исследования:

- случайности остаточной компоненты по критерию пиков;

- нормальности распределения остаточной компоненты по R/S-критерию с критическими значениями от 3 до 4,21.

Для проверки случайности остатков рассмотрим график остатков

График 1

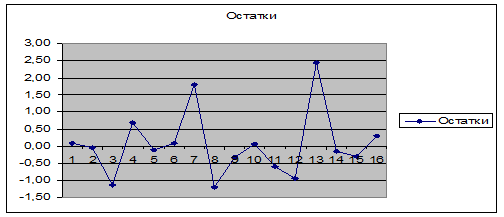
По графику найдем количество поворотных точек – это точки максимума и минимума. => Р=9.

Определим по формуле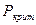

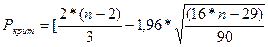При n=16 получим

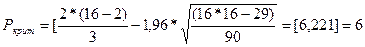
Так как Р=9>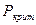=6 => свойство случайности остатков выполняется.

Проверка независимости остатков по d – критерию

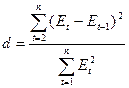
Подготовим 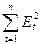, с помощью функций табличного процессора Microsoft Excel СУММКВ и СУКВРАЗН (Мастер функции/Категория – Математические/СУММКВ; Мастер функции/Категория – Математические/СУММКВРАЗН) => 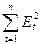=13,89; =36,86 =>

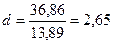
Так как d=2,65 > 2, то величину d уточним, т.е. d=4-2,65=1,35

Критические значения равны 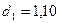и 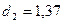(по условию задачи); d=1,35>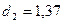, т.е. 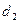< d<2 => уровни ряда остатков является независимыми.

Проверим отсутствие автокорреляция по первому коэффициенту автокорреляции.

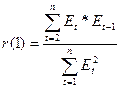
Подготовим 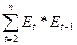с помощью табличного процессора Microsoft Excel СУММПРОИЗВ (Мастер функции/Категория – Математические/СУММПРОИЗВ) => 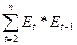= -4,59 => .

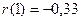Критическое значение 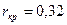(по условию задачи).

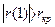=> свойство независимости остаточной компоненты не выполняется.

Рассчитаем значения R/S по формуле

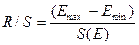
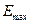и 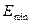найдем с помощью табличного процессора Microsoft Excel МАКС и МИН (Мастер функции/Категория – Статистические/МАКС; Мастер функции/Категория – Статистические/МИН ) => 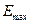=2,43; 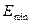=-1,20

S(E) найдем с помощью табличного процессора Microsoft Excel (Мастер функции/Категория – Статистические/СТАНДОТКЛОН) => S(E)=0,96

Получим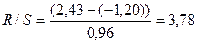

Полученное значение R/S сравним с табличными значениями [3;4,21] => R/S=3,78 входит в критический интервал => свойство нормального распределения остатков выполняется.

Таким образом, по точности модель удовлетворительна, но не является адекватной, так как не выполняется свойство независимости остатков. Прогноз по этой модели проводить нецелесообразно.

4. Построить точечный прогноз на 4 шага вперед, т.е. на 1 год.

Составим прогноз на 4 квартала вперед (т.е. на 1 год, с t=18 по t=20).

Для первого квартала будущего года положим в основной формуле модели Хольта-Уинтерса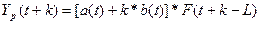

t=16, k=1 и найдем

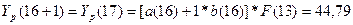
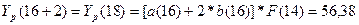
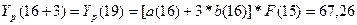
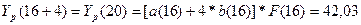
5. Отразить на графике фактические, расчетные и прогнозные данные.

График2

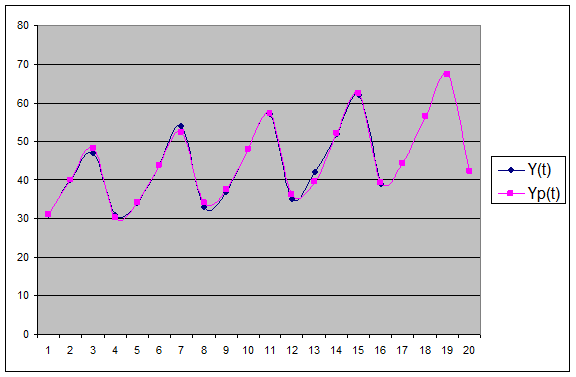
Из графика видно, что расчетные данные согласуются с фактическими, что говорит об удовлетворительном качестве прогноза.

Задание 2

Даны цены (максимальная, минимальная и закрытия) за 10 дней. Интервал сглаживания принять равным пяти дням.

Требуется рассчитать:

а) экспоненциальную скользящую среднюю;

б) момент;

в) скорость изменения цен;

г) индекс относительной силы;

д) %R, %K, %D.

Расчеты проводить для всех дней, для которых эти расчеты можно выполнить на основании имеющихся данных.

Таблица7

дни	цены
макс.	мин.	закр.

1	735	701	715
2	750	715	738
3	745	715	720
4	725	707	712
5	738	702	723
6	747	716	744
7	835	755	835
8	875	812	827
9	853	821	838
10	820	760	767

Решение

а) Найдем экспоненциальную скользящую среднюю

Экспоненциальная скользящая средняя рассчитывается по формуле

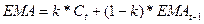, где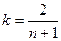

n=5 (по условию задачи) => расчет начинаем с пятой строки.

Для определения начального значения 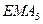используем формулу простой скользящей средней, т.е. 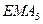≈ МА.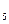

Простую скользящую среднюю найдем с помощью табличного процессора Microsoft Excel (Мастер функции/Категория – Статистические/СРЗНАЧ) и получим

МА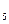≈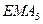=721,6

Дальнейшие расчеты выполним по формуле экспоненциальной скользящей средней при 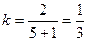. Получим

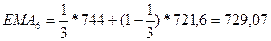
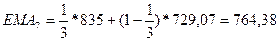
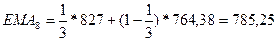
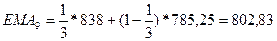
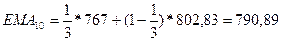
Покажем исходные цены закрытия и найденную экспоненциальную среднюю на графике, проведем анализ.

График 3

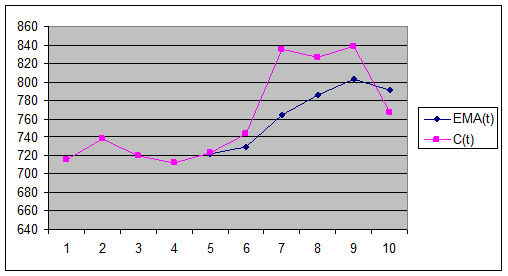
С 5-го по 9-ый день ЕМА(t) ниже чем С(t) => рекомендуются покупки.

В 10-ый день графики пересекаются, это сигнал разворота к продажам.

б) момент

Рассчитаем момент по формуле 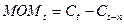, где t>n+1 => расчет выполняем с шестого уровня, т.е.

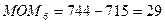
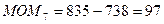
и т.д.

Результаты вычислений занесем в соответствующий столбец расчетной таблицы

Таблица8

t	C(t)	MOM(t)
1	715
2	738
3	720
4	712
5	723
6	744	29
7	835	97
8	827	107
9	838	126
10	767	44

Покажем на графике линию момента

График 4

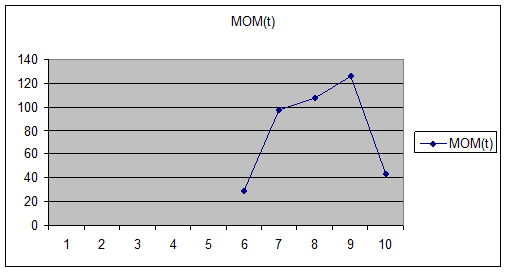
С 6-го по 10-ый день график момента целиком находится в области выше нулевого уровня; рекомендуется покупка. Сигнала разворота нет.

в) скорость изменения цен

Для расчета используем формулу

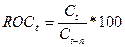
n=5 (по условию), t≥n+1 => t=6 =>

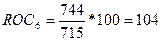
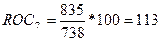
и т.д.

Результаты вычислений занесем в соответствующий столбец расчетной таблицы

Таблица9

t	C(t)	ROC(t)	t	C(t)	ROC(t)
1	715		9	838	118
2	738		10	767	106
3	720
4	712
5	723
6	744	104
7	835	113
8	827	115

Покажем на графике линию скорости изменения цен

График5

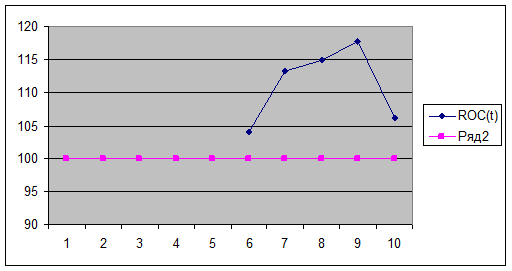
График скорости изменения цен целиком находится в области выше уровня 100%; с 6-го по 10-ый день рекомендуется покупки. Сигнала разворота нет.

г) индекс относительной силы

Для использования формулы расчета индикатора RSI

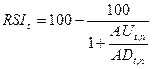предварительно найдем изменение цен закрытия 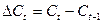, для всех дней t≥2.

Из значений 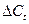выберем положительные, характеризующие повышение цен, и отрицательные, показывающие понижение цен с помощью функции ЕСЛИ табличного процессора Microsoft Excel (Мастер функции/Категория – Логические/ЕСЛИ).

Для всех t≥6 рассчитаем суммы приростов и суммы убыли закрытия за 5 дней до дня t (n=5 задано по условию) с помощью функции СУММ табличного процессора Microsoft Excel (Мастер функции/Категория – Математические/СУММ).

Результаты вычислений занесем в соответствующие столбцы расчетной таблицы

Таблица10

t	C(t)	изменен.	повышен.	понижен.	AU(t,5)	AD(t,5)	RSI(t)
1	715
2	738	23	23	0
3	720	-18	0	18
4	712	-8	0	8
5	723	11	11	0
6	744	21	21	0	55	26	68
7	835	91	91	0	123	26	83
8	827	-8	0	8	123	16	88
9	838	11	11	0	134	8	94
10	767	-71	0	71	123	79	61

Теперь найдем величины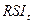

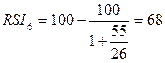
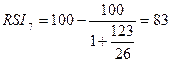
и т.д.

Результаты вычислений занесем в соответствующий столбец расчетной Таблицы 10.

Рассмотрим график RSI:

График6

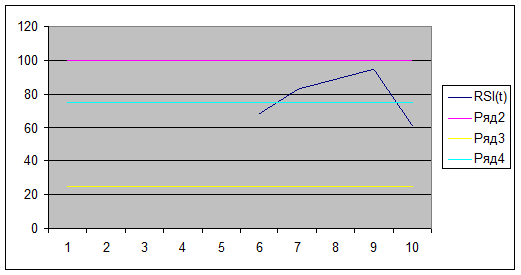
6-ой день – график находится в нейтральной зоне, можно проводить финансовые операции в соответствии с сигналами других индексов.

7-10 дни – график в зоне «перекупленности», ожидается разворот.

10 день – график вышел из зоны «перекупленности», что является сигналом разворота тренда, рекомендуется начать продажи.

д) %R, %K, %D

Для расчета стохастических индексов необходима полная информация: - минимальная и максимальная цена (, );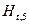

- ;

- .

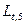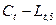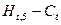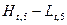Расчет возможен для t≥5.

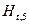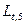1. Заполним столбцы и начиная с пятой строки с помощью функций МИН и МАКС табличного процессора Microsoft Excel (Мастер функции/Категория – Статистические/МИН; Мастер функции/Категория – Статистические/МАКС).

Таблица 11

t	H(t,5)	L(t,5)
1
2
3
4
5	750	701
6	750	702
7	835	702
8	875	702
9	875	702
10	875	716

2. Заполним столбцы разницы , ,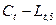

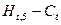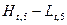
Таблица 12

t	C(t)-L(t,5)	H(t,5)-C(t)	H(t,5)-L(t,5)
1
2
3
4
5	22	27	49
6	42	6	48
7	133	0	133
8	125	48	173
9	136	37	173
10	51	108	159

3. Вычислим индексы %К и %R по формулам

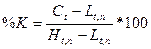
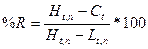
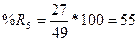
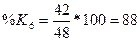
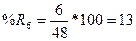
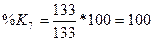
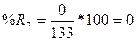
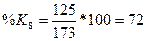
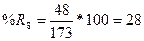
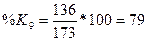
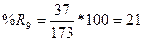
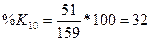
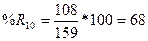
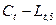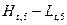4. Вычислим трехдневные суммы для () и (), начиная с (n+2) дня, т.е. начинаем с седьмого уровня. Для нахождения трехдневной суммы воспользуемся функцией СУММ табличного процессора Microsoft Excel (Мастер функции/Категория – Математические/СУММ).

Таблица13

t	C(t)-L(t,5)	H(t,5)-L(t,5)	%K	%R	sum(C-L)	sum(H-L)
1
2
3
4
5	22	49	45	55
6	42	48	88	13
7	133	133	100	0	197	230
8	125	173	72	28	300	354
9	136	173	79	21	394	479
10	51	159	32	68	312	505

5. Вычислим %D по формуле

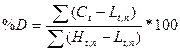
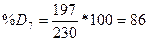
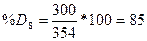
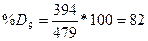
Таблица14

Итоговая таблица

t	H(t,5)	L(t,5)	C(t)-L(t,5)	H(t,5)-C(t)	H(t,5)-L(t,5)	%K	%R	sum(C-L)	sum(H-L)	%D
1
2
3
4
5	750	701	22	27	49	45	55
6	750	702	42	6	48	88	13
7	835	702	133	0	133	100	0	197	230	86
8	875	702	125	48	173	72	28	300	354	85
9	875	702	136	37	173	79	21	394	479	82
10	875	716	51	108	159	32	68	312	505	62

Покажем стохастические линии %R, %K, %D на одном графике

График 7

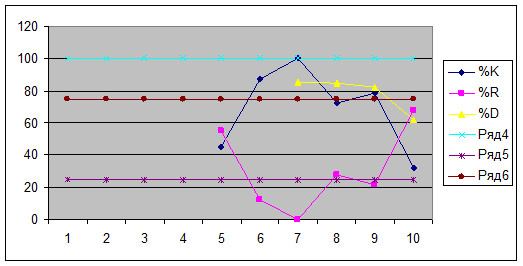
График %К показывает, что в 5-ый день можно совершать финансовые операции в соответствии с сигналами других индексов, т.к. график находиться в нейтральной зоне; 6 – 7 дни рекомендуется прекратить финансовые операции (график находиться в критической зоне «перекупленности»); 8-ой день – выход из критической зоны в нейтральную, рекомендуются продажи, ожидается разворот; выход из нейтральной зоны в критическую, рекомендуется прекратить все финансовые операции; 9-ый день – выход из критической зоны в нейтральную, рекомендуется продажи, сигнал разворота; 10-ый день – можно совершать финансовые операции в соответствии с сигналом других индексов.

График %R является зеркальным отражением графика %К. Для него верхняя критическая зонная является зоной «перепроданности», а нижняя – зоной «перекупленности». Таким образом, выводы по графику %R совпадают с выводами по графику %К.

График %D показывает, что в 7-9 дни находится в критической зоне, рекомендуется остановить все операции; в 10-ый день график выходит из критической зоны, согнал разворота, рекомендуется начать продажи.

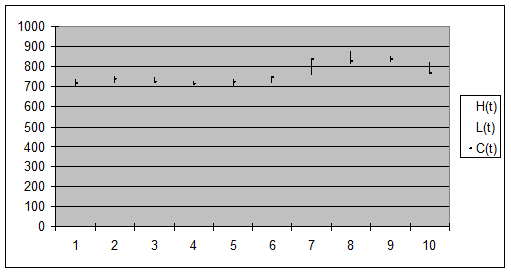
Диаграмма 1

Биржевая диаграмма

Задание 3

Выполнить различные коммерческие расчеты, используя данные, приведенные в таблице. В условии задачи значения параметров введены в виде переменных. Например, S означает некоторую сумму средств в рублях, Т_лет - время в годах, i - ставку в процентах и т.д. По номерам переменных из таблицы необходимо выбрать соответствующие численные значения параметров и выполнить расчеты.

Исходные данные:

Таблица15

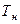
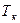
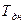
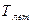
сумма					i	m
1500000	17.01.02	13.03.02	180	4	20	2

3.1. Банк выдал ссуду, размером S руб. Дата выдачи ссуды - T_н, возврата - T_к. День выдачи и день возврата считать за 1 день. Проценты рассчитываются по простой процентной ставке i % годовых.

Найти:

3.1.1) точные проценты с точным числом дней ссуды;

3.1.2) обыкновенные проценты с точным числом дней ссуды;

3.1.3) обыкновенные проценты с приближенным числом дней ссуды.

3.2. Через T_дн дней после подписания договора должник уплатит S руб. Кредит выдан под i % годовых (проценты обыкновенные). Какова первоначальная сумма и дисконт?

3.3. Через T_дн дней предприятие должно получить по векселю S руб. Банк приобрел этот вексель с дисконтом. Банк учел вексель по учетной ставке i % годовых (год равен 360 дням). Определить полученную предприятием сумму и дисконт.

3.4. В кредитном договоре на суммуS руб. и сроком на T_лет лет, зафиксирована ставка сложных процентов, равная i % годовых. Определить наращенную сумму.

3.5. Ссуда размером S руб. предоставлена на Т_лет. Проценты сложные, ставка - i% годовых. Проценты начисляются m раз в году. Вычислить наращенную сумму.

3.6. Вычислить эффективную ставку процента, если банк начисляет проценты m раз в году, исходя из номинальной ставки i % годовых.

3.7. Определить, какой должна быть номинальная ставка при начисленни процентов m раз в году, чтобы обеспечить аффективную ставку i % годовых.

3.8. Через Т_лет предприятию будет выплачена сумма S руб. Определить ее современную стоимость при условии, что применяется сложная процентная ставка i % годовых.

3.9. Через T_лет по векселю должна быть выплачена сумма S руб. Банк учел вексель по сложной учетной ставке i % годовых. Определить дисконт.

3.10. В течение Т_лет лет на расчетный счет в конце каждого года поступает по S руб., на которые m раз в году начисляются проценты по сложной годовой ставке i %. Определить сумму на расчетном счете к концу указанного срока.

Решение

Найти:

3.1.1) точные проценты с точным числом дней ссуды;

3.1.2) обыкновенные проценты с точным числом дней ссуды;

3.1.3) обыкновенные проценты с приближенным числом дней ссуды.

Для расчета точного числа дней ссуды воспользуемся табличным процессором Microsoft Excel – разность между датой закрытия и датой открытия, т.е. t=55 дней.

Простые проценты рассчитываются по формуле

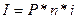, где 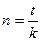, Р=1 500 000 руб., I=20%

3.1.1) Точные проценты с точным числом дней ссуды (АСТ/АСТ):

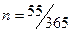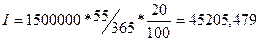=> руб.

3.1.2) Обыкновенные проценты с точным числом дней ссуды (АСТ/360):

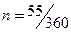=> руб.

Для расчета приближенного числа дней ссуды воспользуемся табличным процессором Microsoft Excel (Мастер функции/Категория – Дата и время/ДНЕЙ360), t=56.

3.1.3) Обыкновенные проценты с приближенным числом дней ссуды (360/360):

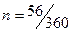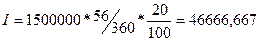=> руб.

Денежная сумма: разовая, S=1 500 000 руб.

Операция: дисконтирование, Р - ?

Проценты: простые => расчет по формулам

Первоначальная сумма для простых процентов рассчитывается по следующей формуле

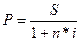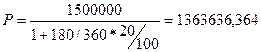, где n=180/360, i=20%, S=1 500 000 руб.

руб.

D=S-P => D=1 500 000-1 363 636,364=136 363,6364 руб.

Денежная сумма: разовая, S=1 500 000 руб.

Операция: дисконтирование, Р - ?

Проценты: простые => расчет по формулам

Первоначальная сумма для простых процентов рассчитывается по следующей формуле

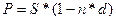, n =180/360, d=20% =>

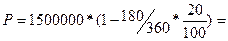=>1 350 000,00 руб.

D=S-P => D=1 500 000-1 350 000,00= 150 000,00 руб.

Денежная сумма: разовая, Р=1 500 000 руб.

Операция: наращение, S- ?

Проценты: сложные => используются функции табличного процессора Microsoft Excel.

Мастер функции/категория – Финансовые/БС

Ставка 20%

Кпер 4

Плт 0

ПС - 1 500 000

Тип 0

=> S=БС=3 110 400, 00 руб.

Денежная сумма: разовая, Р=1 500 000 руб.

Операция: наращение, S- ?

Проценты: сложные => используются функции табличного процессора Microsoft Excel.

Мастер функции/категория – Финансовые/БС

Ставка 20%/2

Кпер 4*2

Плт 0

ПС - 1 500 000

Тип 0

=> S=БС=3 215 383,22 руб.

Для нахождения эффективной ставки процента воспользуемся табличным процессором Microsoft Excel.

Мастер функции/Категория – Финансовые/ЭФФЕКТ

Номинальная ставка 20%

Кол_пер 2

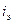=> =ЭФФЕКТ=21%

Для нахождения номинальной ставки процента воспользуемся табличным процессором Microsoft Excel.

Мастер функции/Категория – Финансовые/НОМИНАЛ

Эффект_ставка 20%

Кол_пер 2

=> =НОМИНАЛ=19,09%

Денежная сумма: разовая, S=1 500 000 руб.

Операция: дисконтирование, P- ?

Проценты: сложные => используются функции табличного процессора Microsoft Excel.

Мастер функции/категория – Финансовые/ПС

Ставка 20%

Кпер 4

Плт 0

ПС - 1 500 000

Тип 0

=> Р=ПС=723 379,63 руб.

Денежная сумма: разовая, S=1 500 000 руб.

Операция: дисконтирование, P- ?

Проценты: сложные => используются функции табличного процессора Microsoft Excel.

Мастер функции/категория – Финансовые/БС

Ставка - 20%

Кпер 4

Плт 0

ПС - 1 500 000

Тип 0

=> Р=БС=614 400,00руб.

D=S-P => D=1 500 000-614 400,00=885 600,00 руб.

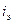По условию задана номинальная ставка =20%, требуется найти эффективную ставку при начислении 2 раза в год m=2.

Для нахождения эффективной ставки процента воспользуемся табличным процессором Microsoft Excel.

Мастер функции/Категория – Финансовые/ЭФФЕКТ

Номинальная ставка 20%

Кол_пер 2

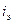=> =ЭФФЕКТ=21%

Денежная сумма: платежи, R=1 500 000 руб. 1 раз в год

Операция: наращение, S- ?

Проценты: сложные => используются функции табличного процессора Microsoft Excel.

Мастер функции/категория – Финансовые/БС

Ставка 21%

Кпер 4

Плт -1 500 000

ПС 0

Тип 0

=> S=БС=8 168 491,50руб.