Содержание
Задача 1. 3
Задача 2. 4
Задача 3. 5
Задача 4. 7
Задача 5. 9
Список литературы.. 11
Задача
1
На основании нижеприведенных данных
определить средний размер заработной платы одного работника в целом по
предприятию и за 1 и 2 квартал отдельно и за два квартала в целом. Написать
наименование и формулы средних, которые использовались. Сделать выводы.
|
Цех
предприятия
|
1 квартал
|
2 квартал
|
|
Средняя з/п,
руб.
|
Количество
работников
|
Средняя з/п,
руб.
|
Фонд оплаты
труда, руб.
|
|
1
|
6500
|
120
|
7000
|
875000
|
|
2
|
4200
|
40
|
5400
|
226800
|
|
3
|
5900
|
90
|
6300
|
617400
|
Решение:
Определим
среднюю зарплату (f) по предприятию за первый квартал, для этого используем формулу средней
взвешенной (5, стр. 101):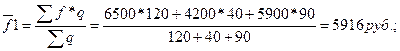 
Для
нахождения средней зарплаты за второй квартал используем формулу средней
гармонической
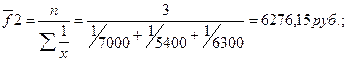
Для
определения средней зарплаты за полугодие используем формулу средней
арифметической: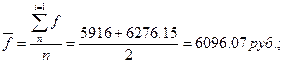 
Вывод: по итогам расчётов мы выявили рост
средней заработной платы в целом по предприятию во втором квартале. Несмотря на
рост численности работников во втором квартале, рост средней заработной платы в
каждом цехе позволил добиться общего роста по предприятию. Из-за того, что
наивысшая зарплата в цехе №1, где работает большинство сотрудников, средняя
зарплата за полугодие превышает среднюю зарплату по 2 и 3 цеху, где работает
меньше персонала.
Задача 2
На основании данных о себестоимости
обработки изделий при ручном и автоматизированном способах обработки
определить:
1.
Индивидуальные индексы себестоимости;
2.
Общий индекс себестоимости в агрегатной форме;
3.
Величину реальной экономии, которую получает предприятие
за счёт снижения себестоимости продукции.
|
Способы
|
Объём
продукции, тыс. изд.
|
Себестоимость
обработки одного изделия, руб.
|
|
Базисный
|
Отчётный
|
Базисный
|
Отчётный
|
|
Ручной
|
2800
|
12500
|
20
|
18
|
|
Автоматизированный
|
1300
|
3200
|
15
|
12
|
Решение:
Индивидуальный индекс себестоимости
находится по формуле: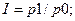
(5, стр. 139)
рассчитаем следующие индивидуальные индексы:
Ручная
обработка: I = 18 / 20 = 0.9;
Автоматизированная
обработка: I = 12 / 15 =
0,8;
Таким образом,
построим таблицу, куда занесём темпы показателей:
|
Способы
|
Темп роста
объёма продукции, тыс. изд.
|
Темп роста себестоимости обработки одного
изделия, руб.
|
|
Ручной
|
4,46
|
0,9
|
|
Автоматизированный
|
2,46
|
0,8
|
Общий индекс себестоимости в
агрегатной форме рассчитывается по формуле: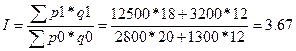 
.
Этот индекс, согласно условию задачи,
нужно найти, но он потом нигде не используется.
Сумма экономии будет равна
произведению разницы себестоимости на однодневный выпуск продукции в отчётном
периоде. Сумма общей экономии будет равна сумме экономий по каждому способу
обработки: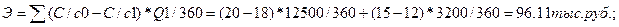
Вывод: Таким образом, за счёт снижения
индивидуальных индексов себестоимости, как при ручной, так и при автоматической
обработке в отчётном периоде по сравнению с базисным, а также улучшения
использования оборотных средств на предприятии, была достигнута экономия
денежных средств в размере 96,11 тыс. руб.
Задача 3
Оценить динамику показателей
использования оборотных средств. Рассчитать, сколько высвободиться оборотных
средств из оборота, если длительность одного оборота сократить на три дня.
|
Показатели
|
Базисный год
|
Отчётный год
|
|
Объём продукции (V), тыс. руб.
|
2900
|
3340
|
|
Среднегодовая стоимость оборотных
средств (ОбС), тыс. руб.
|
270
|
|
Решение:
Показателями использования оборотных
средств являются:
·
Коэффициент оборачиваемости Коб = V / ОбС;
·
Длительность одного оборота в днях ДО = 360 / Коб;
1)Оборачиваемость
в базисном году составила: Коб = 2900 / 270 = 10,74 оборотов;
Продолжительность одного оборота: ДО = 360
/ 10,74 = 33,51 дня;
2)Продолжительность
одного оборота в отчётном году: 33,51 – 3 = 30,51 дней;
Оборачиваемость в отчётном году: Коб = 360
/ 30,51 = 11,79 оборотов;
Среднегодовая стоимость оборотных средств:
ОбС = V / Коб = 3340 / 11,79 = 283,29 тыс. руб.;
3) Динамика показателей
использования оборотных средств выглядит следующим образом:
Темп роста оборачиваемости =
11,79 / 10,74 = 1,097 (иными словами оборачиваемость выросла в отчётном году по
сравнению с базисным на 9,7%);
Темп роста продолжительности
одного оборота = 30,51 / 33,51 = 0,91 ( т.е. продолжительность одного оборота
снизилась на 9%).
Высвобождение оборотных средств
равняется произведению ускорения оборачиваемости на однодневный выпуск
продукции в отчётном году = (11,79 – 10,74) * 283,29 / 360 = 0,826 тыс. руб.;
Вывод: При сокращении длительности одного
оборота на три дня произойдёт ускорения
оборачиваемости, за счёт чего, из оборота высвободится 826 руб. налицо динамика
показателей оборачиваемости ускорение длительности одного оборота на 3 дня и
увеличение количества оборотов с 10,74 до 11,79 оборотов в год.
Задача 4
Рассчитать перспективную численность
населения на два последующих года с помощью аналитического выравнивания.
Динамический ряд изобразить графически.
|
Годы
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
Численность населения, тыс. чел.
|
750
|
752
|
755
|
760
|
762
|
?
|
?
|
Решение:
Проведём аналитическое выравнивание с
помощью линейной трендовой модели, для
этого найдём средний уровень прироста (разница между данным и предыдущим
показателем):
|
Годы
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
Численность населения, тыс. чел.
|
750
|
752
|
755
|
760
|
762
|
?
|
?
|
|
Уровень прироста
|
-
|
2
|
3
|
5
|
2
|
|
|
Средний уровень прироста найдём с
помощью формулы средней арифметической: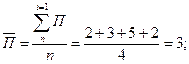 
Выдвигаем
гипотезу о наличие линейного тренда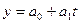 
.
Определяем коээфициенты линейного тренда. Для этого
используем табличный редактор EXCEL, функцию: ЛИНЕЙН,
получим:
|
а1
|
а0
|
|
tфактич
|
6,22667027
|
760,607533
|
|
t табл
|
1.859
|
1.859
|
|
Вывод
|
значим
|
значим
|
Если неравенство
tфакт > tтабл справедливо, то это означает, что коэффициент аi значим, т.е.
существенно отличен от нуля, и соответствующая переменная хi должна быть
включена в уравнение тренда, так как она оказывает существенное влияние на
зависимую переменную у. В нашем случае линейный тренд существует.
В силу существования линейного тренда
осуществим аналитическое выравнивание уравнением линейной регрессии. Для этого
воспользуемся встроенными функциями пакета Excel.
Изобразим
динамический ряд роста численности населения, график уравнения линейной
регрессии с помощью пакета Excel, а также с помощью этого пакета получим уравнение
линейного тренда:
Следует
заметить, что значение коэффициента детерминации 0,9771 говорит о том, что
переменная у почти на 98% зависит от х, что подтверждает гипотезу и
существовании тренда.
Для
прогнозирования численности населения в годы 6 и 7 воспользуемся полученным
линейным уравнением:
y(x) = 3.2x + 746.2
y(6) = 3.2×6 + 746.2 =
765.4 тыс. ч.
y(7) = 3.2×7 + 746.2 =
768.6 тыс. ч.
Вывод: Имеем устойчивую
тенденцию (линейный тренд) к росту численности населения, что отчётливо видно и
на графике. Выполнив аналитическое выравнивание с помощью уравнения линейной
регрессии, и осуществив прогноз по этому уравнению, получим следующие
прогнозные данные по численности населения:
6
год: 765.4 тыс. ч.
7
год: 768.6 тыс. ч.
Задача 5
Численность занятых в составе
экономически активного населения – 85 млн. чел., численность безработных – 15
млн. чел. Месяц спустя из 85 млн. чел., имевших работу были уволены и ищут
работу 0,5 млн. чел., 1 млн. чел. из числа официально зарегистрированных
безработных прекратили поиски работы.
Определить:
·
Начальный уровень безработицы;
·
Численность занятых, количество безработных и уровень
безработицы месяц спустя.
Решение:
Уровень безработицы определяется, как
отношения числа безработных к численности экономически активного населения.
Начальный уровень безработицы 15 / 85
= 0,176;
Месяц спустя:
Численность занятых = 85 – 0,5 = 84,5
млн. чел. (было уволено 0,5 млн. чел.);
Количество безработных = 15 – 1 + 0,5
= 14,5 млн.чел.;
Т.к. 1 млн. чел. прекратили поиски
работы, следовательно их нельзя считать экономически активными.
Уровень безработицы 14,5 / 84,5 =
0,171;
Вывод: Таким образом, за счёт снижения общего
числа экономически активного населения и числа безработных, уровень безработицы
спустя месяц снизился на 0,006;
Список литературы
1.
Бочков А. И. Статистика. – М.: «Финансы и статистика»,
2003.
2.
Иванова Ю. Н. Экономическая статистика. – М.: «Инфра-М»,
1998.
3.
Назаров М. Г. Статистика финансов. – М.: «Дело», 2003.
4.
Салин В. Ф. Статистика финансов. – М.: «Финансы и
статистика», 2000.
5.
Харченко Л. П. Статистика. – М.: «Инфра-М», 2002.