Иерархия материального мира

Качественные структуры позволили не только описать весь мир, но и выделить тип процессов который превалирует на каждом уровне.

Сегодняшней наукой мало изучен вакуум, идет поиск наиэлементарнейших частиц, на данный момент самые малые гипотетические частицы это кварки (их существование вывели теоретически).

Данная таблица позволяет структурировать любой объект из наиболее малых (т.е. №13). Среди этих объектов, в зависимости от размера, можно выделить структуры относящиеся к мегамиру, макромиру, микромиру. Помимо этого иногда включается понятие мезоуровень, который находится между макро и микроуровнем. Для науки является важным установление единых законов на каждом уровне.

Предпринята попытка систематизировать мир в его изменчивости, было доказано, что мир это не хаотическое скопление предметов и явлений, а системное образование.

Данная таблица показывает, что в природе существует (проступает) иерархия структурных уровней организации материи (микро и макро уровень). Каждый уровень имеет свою специфику и характеризуется своими размерами, он еще закономерным образом связан с другими уровнями. Иерархия структур это природное явление или искусственное создание ученых? Суть в том, что методология была создана наукой и позволила объяснить новые явления, с другой стороны мы все в одном мире, и иерархия уровней скорее искусственное образование, которое создано для облегчения понимания мира. Цель ученых не только установить специфику организации уровней, но и установить связи между уровнями. Именно это является причиной создания единой теории сущего, во всем его многообразии форм.

1. Метагалактика - это изученная путем доступного наблюдения часть Вселенной со всеми находящимися в ней галактиками и другими объектами. Считается, что метагалактика включает в себя несколько миллиардов галактик, и по некоторым представлениям, составляет незначительную часть Вселенной.

2. Ячеистая структура - речь идет о расположении галактик (равномерно или неравномерно). На сей счет, есть некоторые гипотезы. Так, эстонские астрономы путем моделирования вывели модель расположения галактик. В соответствии с этой моделью оказалось, что в расположении лежит определенная закономерность. Характер расположения напоминает расположения пчелиных сот. Оказалось что галактики расположены вдоль условных стенок условных сот. А внутри - так называемые пустоты или воиды. Кроме этого наибольшие скопления галактик расположены в местах пересечения стенок.

3. Скопления галактик - имеют почти сферическую форму, в них насчитывают сотни и тысячи галактик. Ближайшее к нам скопление галактик находится в созвездии Девы и насчитывает порядка трех тысяч галактик. В настоящее время изучены малочисленные группы галактик, в них входят две большие спиральные галактики: в частности, Млечный путь и туманность Андромеды. Кроме того, каждая из этих спиральных галактик имеет группы галактик - спутников. В частности у нашей галактики в числе спутников являются большое и малое Магелановы облака. Всего в нашей группе насчитывается 38 галактик. А всего на данный момент известно до нескольких десятков подобных групп.

4. Галактики - это звездные системы, которые связаны между собой гравитационным притяжением. Галактики подразделяют по форме на: спиральные, эллиптические и неправильные. Обнаружение галактик происходит по свечению большого количества звезд в галактиках. В состав галактики входит газ (водород и гелий) и пыль, их масса составляет только несколько процентов от массы звезд, но в свою очередь суммарная масса звезд, газа и пыли составляет одну десятую доли от полной массы галактики. Отсюда следует что 9/10 всего вещества в галактике находится в невидимой или скрытой форме. Полагают, что эта загадочная скрытая масса - невидимое вещество, расположенное во внешних частях (коронах) галактики. Оно сосредоточено в виде слабо светящегося газа, многочисленных так и не загоревшихся звезд и темных планет. Проблема скрытой массы одна из наиболее изучаемых проблем современной астрофизики. Существует определенный метод определения массы и установлено, что массы галактик изменяются в пределах от 10 в 9 (степени) до 10 в 12 (степени) массы солнца.

5. Звездные скопления - это гравитационно-связанные группы звезд, имеющих общее происхождение, которые движутся в поле тяготения галактик как единое целое.

6. Звезды - это основная структурная единица мегамира. Все видимое излучение во Вселенной приходится на долю звезд. Звезды - это природные термоядерные реакции, в которых происходит химическая эволюция вещества и его переработка. Звезды имеют определенные особенности в своей жизни, это значит, что одна и та же звезда в зависимости от массы и возраста проходит различные эволюционные фазы. Условно разделяют все звезды на две большие группы:

-         обыкновенные или нормальные звезды, размеры этих звезд изменяются в пределах чуть меньше нашего солнца до сверх гигантов (10 в 8, 10 в 11);

-         нейтронные звезды, белые карлики, черные дыры, т.е. ко второй группе относятся продукты конечной эволюции звезд.

Планеты - это небесные тела менее массивные, чем звезды. Планеты вращаются вокруг какой либо звезды и светятся отраженным светом.

Солнечная система

Первые четыре из небесных тел сложены из твердого вещества и называются планетами земной группы, т.е. все они в каком-то виде имеют атмосферу, но только на земле есть океаны и текучая вода. Следующие четыре планеты - планеты-гиганты, состоящие из газа. Девятая планета получает очень мало тепла и состоит главным образом изо льда. Важно, что все планеты солнечной системы вращаются примерно в одной плоскости по орбитам.

8. Макроскопические тела. Размеры этих тел от 0.1 мм до 1 метра.

9. Микроскопические тела - это объединение молекул или молекулярные структуры, типичный пример этой структуры - это клетка живой структуры. Если мы говорим о твердых телах, то можем выделить элементы кристаллической решетки и ее параметры.

10. Макромолекулы - это ДНК и РНК. Это довольно асимметричные структуры. Нынешние полимерные материалы тоже могут составлять макромолекулы.

Термодинамический и статистический методы описания систем

Хаотическое поведение может возникать даже в очень простых системах, например, из физических моделей  – в колебаниях сферического маятника с двумя степенями свободы. Мы для начала рассмотрим даже ещё более простые математические модели с дискретным временем – сдвиг Бернулли и преобразование пекаря.

Сдвиг Бернулли представляет собой отображение в одномерном пространстве на интервале (0,1) по закону

x_n+1=2x_n(mod1).

Это уравнение движения детерминистично: по заданному x_n однозначно вычисляется x_n+1. При этом, однако, сдвиг Бернулли не является обратимым отображением. Симметрия во времени нарушена ещё на уровне уравнения движения. Этим сдвиг Бернулли отличается от динамических систем с обратимыми уравнениями движения.

Сдвиг Бернулли представляет собой пример детерминистического хаоса. Можно представить примеры последовательностей, начинающихся с какого-нибудь произвольного числа, например:

{0.13;  0.26;  0.52;  0.04;  0.08;  0.16;  0.32;  0.64;  0.28...   }

и

{0.14;  0.28;  0.56;  0.12;  0.24;  0.48;  0.96;  0.92;  0.84... } –

как видим, незначительное отличие в начальных условиях уже на 4-м шаге порождает существенное различие траекторий, а в дальнейшем их поведение совершенно различно.

Легко показать, что со временем разойдутся траектории любых двух сколь угодно близких точек. Запишем число x в виде двоичной дроби:

x=0.u_–1u_–2u_–3...u_–k...=u_–1/2 + u_–2/2² + u_–3/2³ + ... + u_–k/2^k + ...

Описанное выше отображение соответствует сдвигу u_–k'=u_–(k+1) , откуда становится понятным название "сдвиг Бернулли". Видно, что нулевой разряд числа при этом теряется, что соответствует невзаимооднозначности отображения.

Описание эволюции динамической системы типа сдвига Бернулли в терминах траектории неадекватно, так как для адекватности траектория должна оставаться "почти одной и той же" при незначительном изменении начальных условий.

В данном же случае имеет смысл обратиться к статистическому описанию, введя плотность вероятности r(x) пребывания системы в каждой точке x интервала (0,1). Отображение представляет собой оператор U, действующий на эту функцию:

r_n+1=Ur_n(x)= ( r_n(x/2)+r_n((x+1)/2) ) / 2.

Оказывается, что при многократном применении оператора отображения к произвольному распределению плотности вероятности оно стремится к константе:

r_n=Uⁿr₀(x)®r_µ(x)=const.

 В дальнейшем мы ещё вернемся к отображению Бернулли и свойствам его оператора, а пока рассмотрим другую простую динамическую систему, теперь уже двумерную, называемую преобразованием пекаря:

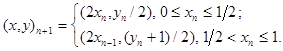
Правило, определяющее преобразование пекаря, очень просто. Сначала квадрат со стороной, равной 1, сплющивается в прямоугольник длиной 2 и высотой 1/2, затем правая половина полученного прямоугольника накладывается на левую, образуя новый квадрат. Процесс в чём-то аналогичен размешиванию теста, отсюда и название.

В отличие от сдвига Бернулли преобразование пекаря обратимо во времени. Однако оно точно так же порождает хаотическое движение, связанное с неустойчивостью по начальным условиям.

Преобразование пекаря сводится к сдвигу в двусторонней двоичной последовательности:

x0y = ....u_–k...u_–3u_-2u_–1u₀u₁u₂...u_k....,

u_k' = u_–(k+1).

Видно, что при этом никакие двоичные разряды не теряются, что и соответствует обратимости преобразования пекаря во времени.

Аналогично сдвигу Бернулли, преобразование пекаря порождает динамический хаос, и описание движения точки в терминах траекторий также неадекватно.

В случае преобразования пекаря описание эволюции системы в статистических терминах даже более "физически осмысленно", чем для сдвига Бернулли. Дело в том, что теперь, в двумерном случае, можно рассматривать координатную плоскость как фазовое пространство некоторой динамической системы с одной степенью свободы: ось x соответствует координате, а ось y – импульсу. Аналогия с "физическими" динамическими системами усиливается ещё и тем, что выполняется теорема Лиувилля: сохраняется объём в фазовом пространстве. Другими словами, взяв ансамбль точек внутри некоторой области и проделав произвольное количество преобразований пекаря, мы обнаружим тоже самое количество точек внутри некоторой другой области (форма её при этом очень сильно изменится и станет крайне замысловатой). Объём этой области (в нашем двумерном случае ему соответствует площадь) останется неизменным.

Несмотря на обратимость преобразования пекаря во времени, эволюция при t ® +µ и при t ® –µ оказывается различной [1,c.114].

Кроме описанных выше, существует ещё много сравнительно простых моделей динамического хаоса. Однако мы воздержимся от их подробного рассмотрения, и перейдём теперь к причинам, лежащим в основе непредсказуемого поведения физических систем.

Классический хаос: неинтегрируемые системы Пуанкаре

Чем простое отличается от сложного? Традиционный ответ содержит ссылку на иерархию. На одном конце шкалы мы находим такие объекты, как маятник, подчиняющийся простым детерминистским законам. На другом конце шкалы находятся люди и их сообщества. Между этими полюсами можно мысленно вписать целую иерархию "комплексификации" – возникновения сложного из простого. В действительности же дело обстоит даже более тонко: простое и сложное могут сосуществовать вместе, не будучи связаны между собой иерархически.

Что касается человеческих сообществ, теория их поведения крайне трудно поддаётся хоть какой-нибудь математизации и заслуживает отдельного рассмотрения, вне рамок настоящей работы. Пример же хаотического поведения простейших физических систем типа маятника будет рассмотрен ниже.

При исследовании того, как простое относится к сложному, обычно широко используется понятие аттрактора, то есть конечного состояния или хода эволюции диссипативной системы. Смысл этого понятия был глубоко преобразован современной физикой и математикой. В прошлом считалось, что все системы, эволюция которых связана с существованием аттрактора, одинаковы. Ныне понятие аттрактора связывают с разнообразием диссипативных систем.

Идеальный маятник без трения не имеет аттрактора и колеблется бесконечно. С другой стороны, движение реального маятника – диссипативной системы, движение которой включает трение, – постепенно останавливается в положении равновесия. Это положение является аттрактором. Аналогичным образом, аттрактором является и состояние термодинамического равновесия: ансамбль из миллиардов и миллиардов частиц, образующих изолированную систему, эволюционирует к состоянию равновесия, описание которого зависит лишь от немногих параметров, таких как температура и давление.

Идеальный маятник служит примером так называемой структурной неустойчивости: в отсутствие трения аттрактор не существует, но введение даже самого незначительного трения изменяет движение маятника и вводит аттрактор.

Чтобы представить аттрактор геометрически, обычно вводят пространство, размерность которого совпадает с числом переменных, необходимых для описания системы. Это могут быть координаты, импульсы, различные термодинамические переменные. Во введённом пространстве равновесное состояние диссипативных систем соответствует точечному аттрактору. То же относится и к стационарным состояниям систем, близких к термодинамическому равновесию и удовлетворяющим теореме о минимальном производстве энтропии. Во всех случаях, каково бы ни было первоначальное приготовление системы, её эволюция может быть описана траекторией, ведущей из точки, которая представляет начальное состояние, к аттрактору. Таким образом, конечная точка – аттрактор – представляет собой финальное состояние всех траекторий.

Не все диссипативные системы приводят к одной-единственной конечной точке. Например, сильно неравновесная диссипативная структура, известная под названием "химические часы", эволюционирует не к какому-нибудь состоянию, а к устойчивому периодическому режиму. Такая ситуация приводит к необходимости обобщения идеи аттрактора: аттрактор более не точка, а линия, описывающая периодическое во времени изменение концентрации химических веществ. Примеры подобных аттракторов легко найти, например, и в радиофизике – ими являются предельные циклы автогенераторов, – и во многих других разделах естествознания.

Система с предельным циклом остаётся предсказуемой и потому допускает простое описание. Но за этой простотой кроются неожиданные свойства. Нетрудно представить себе химическое равновесие – множество химических процессов, компенсирующих друг друга подобно тому, как в состоянии демографического равновесия рождаемость компенсирует смертность. Но воображение бессильно представить себе, как огромные количества молекул, взаимодействующих только через столкновения, начинают вдруг действовать "дружно" – так, что среда периодически изменяет свой цвет.

В других случаях, пытаясь построить изображение аттрактора, мы получим не точку или замкнутую линию, а поверхность или объём. Поворотным же событием стало открытие аттракторов, не относящихся к столь простым геометрическим объектам – так называемым странных аттракторов. В отличие от линии или поверхности, странные аттракторы представляют собой фрактальные объекты, характеризующиеся дробной размерностью.

Странные аттракторы были обнаружены в поведении многих динамических систем, описываемых детерминистическими уравнениями движения. Например, они возникают для так называемого сферического маятника – обыкновенного грузика на нитке, который совершает колебания не в плоскости, а по поверхности полусферы. При внесении возмущений в виде колебаний точки подвеса в некоторый критический момент (зависящий от частоты возмущения) движение маятника становится хаотическим, а его траектория описывается странным аттрактором [1, с.83].

Корреляционный анализ временных последовательностей, характеризующих работу человеческого мозга, изменения климата на планете за миллионы лет и курса акций на бирже также приводит к обнаружению странных аттракторов. Впрочем, при наличии огромного количества внешних причин, влияющих на поведение всех этих систем, случайность их поведения вроде бы удивления не вызывает, поэтому пока обратим внимание на более загадочное явление. Откуда возникает хаотическое поведение в случае сферического маятника?

Как было показано выше, хаотическое поведение отображений типа сдвига Бернулли связано с неустойчивостью по начальным условиям, а необратимость их во времени – с потерей информации при сдвиге двоичной записи числа. Можно, однако, возразить, что приведённые примеры отображений несколько искусственны, так как в природе не встречается подобных дискретных процессов, да и "вычислительной мощности" природы не хватит на выполнение столь мудрёной операций, как модульная арифметика.

Оказывается, однако, что и на уровне решения обычных уравнений движений (вытекающих из законов Ньютона) для того же маятника возможно получение неустойчивых решений, связанных с так называемой неинтегрируемостью системы по Пуанкаре.

Основная проблема классической механики состоит в расчёте движения взаимодействующих тел на основе их уравнений движения (в частном случае, например, это может быть закон Ньютона F=ma). Обобщение ньютоновской механики на более сложные системы показало, что более удобной формой описания является не зависимость от времени пространственной траектории системы (в нашем примере – координаты), а движение точки, изображающей систему, в пространстве вдвое большей размерности, чем обычное "физическое". В общем случае состояние динамической системы описывается координатами q₁, ..., q_s, которые являются независимыми переменными, и соответствующими им импульсами p₁, ..., p_s. Преимуществом такого подхода является существенное упрощение уравнений движения.

Центральная величина всей гамильтоновой механики – функция Гамильтона, или гамильтониан – это, в простейшем случае, выраженная через координаты и импульсы энергия системы (Строгое изложение гамильтоновой механики – см. [3]). В гамильтоновском описании число независимых переменных удваивается, но уравнения движения существенно упрощаются. Рассмотрим систему N точек. Каждой из 3N координат N точек соответствует каноническое уравнение движения 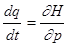. Аналогично, каждому из 3N импульсов соответствует каноническое уравнение движения вида 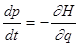 . В качестве частного случая  рассмотрим свободные, то есть невзаимодействующие, частицы. Гамильтониан для них зависит только от импульсов (потенциальной энергии нет). Тогда из канонических уравнений следует, что импульсы постоянны во времени (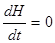), и что координаты, задающие положение частиц, – линейные функции времени. Этот тривиальный случай играет, тем не менее, весьма важную роль в общей проблеме интегрирования гамильтоновых уравнений движения.

Чтобы ввести понятие интегрируемой системы, обратимся к другому простому примеру – маятнику на пружинке, одномерному гармоническому осциллятору. Гамильтониан для него имеет вид 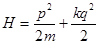, где k – жёсткость пружины, q – смещение груза от положения равновесия. Чтобы упростить уравнения движения, введём новые переменные a и J вместо старых q и p:

,

,

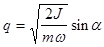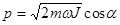где 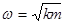– собственная частота колебаний осциллятора. Переменная a называется угловой переменной, J – переменной действия. В переменных угол–действие гамильтониан принимает простой вид: H=w J. Он теперь зависит только от нового импульса – переменной действия. В результате, как и в случае свободных частиц, 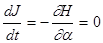, то есть переменная действия является инвариантом движения. Что же касается угловой переменной, то 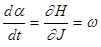, она меняется линейно по времени.

Переход от переменных p, q к переменным J, a называется каноническим преобразованием. В данном случае оно позволило исключить из гамильтониана член, ответственный за потенциальную энергию. Аналогичное преобразование можно иногда проделать и в случае системы со многими степенями свободы, исключив из гамильтониана межчастичное взаимодействие, и выразить движение в циклических переменных. Их название относится к периодическому характеру движения, который делается явным в таких переменных.

Особую важную роль играют частоты системы w₁, w₂, ..., w_n. Именно через эти частоты мы приходим к понятию резонанса, имеющего решающее значение для теоремы Пуанкаре.

Движение интегрируемой системы с двумя степенями свободы можно представить на торе. Возможны две ситуации. Если для некоторых целых n₁ и n₂ выполняется условие  n₁w₁+ n₂w₂=0, то есть частоты соизмеримы, мы имеем резонанс, и движение на торе периодическое – траектория замкнутая. Если же эта сумма ни при каких комбинациях n₁ и n₂ не равна нулю, то траектория навивается на поверхность тора и никогда не замыкается. В конце концов, как показано Пуанкаре, такая траектория проходит сколь угодно близко к произвольной точке на поверхности тора. Траектория при этом называется всюду плотной, а движение – квазипериодическим. Квазипериодическое движение очень сложно выглядит, но на самом деле является вполне детерминированным.

До Пуанкаре полагалось, что все динамические системы являются интегрируемыми. Однако в 1889 г. Пуанкаре показал, что в общем случае невозможно получит каноническое преобразование, сохраняющее вид гамильтоновых уравнений, которое приводило бы к циклическим переменным. Например, система двух тел (Земля – Солнце) интегрируема, а вот система трёх тел (Земля – Солнце – Юпитер) неинтегрируема. Короче говоря, подавляющее большинство динамических систем неинтегрируемы.

Данная работа не посвящена анализу математических методов, которыми Пуанкаре доказывал свою теорему. Отметим только, что он сформулировал свой вопрос в терминах теории возмущений, то есть пытался для гамильтониана вида

H(J,a) = H₀(J)+lV(J,a)

определить новые переменные действия J' вида J' = J + lJ₁ + l²J₂+ ..., аналитически переходящие в исходные при стремлении константы связи l (параметра, определяющего интенсивность взаимодействия) к нулю. Если такая замена возможна, то мы можем исключить потенциальную энергию возмущённой системы и ввести новый гамильтониан, зависящий только от J'. Интегрирование возмущённой системы было бы в этом случае столь ж простым, так как новые переменные действия были бы постоянными движения. Однако Пуанкаре показал, что такая замена возможна далеко не всегда.

Предположим, что Пуанкаре удалось бы доказать интегрируемость всех динамических систем. Это означало бы, что все динамические движения изоморфны движению свободных (не взаимодействующих) частиц. Разумеется, такая модель не оставляет никакого места для возможности макропроцессов, которые мы наблюдаем ежеминутно. В интегрируемом мире не нашлось бы места ни для самоорганизации, ни для когерентности (в случае, например, диссипативного хаоса).

Пуанкаре не только доказал неинтегрируемость, но и указал на её причину, а именно – на существование резонансов между степенями свободы системы. Именно резонансы сильно связывают степени свободы и не дают возможность исключить взаимодействие. В качестве примера рассмотрим систему с двумя степенями свободы, гамильтониан которой имеет вид

H = H₀(J₁,J₂)+lV(J₁,J₂,a₁,a₂),

представимый в виде суммы невозмущённого интегрируемого гамильтониана и малого возмущения lV. Как показал Пуанкаре, теория возмущений неизбежно приводит к появлению членов с "опасными" знаменателями вида 1/(n₁w₁+n₂w₂). Если частоты соизмеримы и существуют резонансы, то члены ряда теории возмущений расходятся, и им приходится приписывать значение, равное бесконечности. Но это означает, что в физике описания что-то "не так"!

Проблема малых знаменателей была известна ещё астрономам в XIX в. Теорема Пуанкаре показала, что основная трудность – появление расходимостей в решении задач динамики – не может быть устранена и делает невозможным введение циклических переменных для большинства динамических проблем, начиная с проблемы трёх тел.

Открытие неинтегрируемости вызвало определённый пессимизм и недоумение в рядах многих физиков. Макс Борн, например, заметил: "Было бы весьма странно, если бы Природа укрылась от дальнейшего прогресса познания за аналитическими трудностями проблемы многих тел". Только с появлением работ Колмогорова, продолженных Арнольдом и Мозером (так называемой теории КАМ), проблему неинтегрируемости перестали оценивать как сопротивление Природы прогрессу знания, а начали рассматривать как новый отправной пункт дальнейшего развития динамики.

Теория КАМ рассматривает влияние резонансов на траектории. Простой случай гармонического осциллятора с постоянной частотой, не зависящей от переменных действия J, является исключением: частоты, вообще говоря, зависят от значений, принимаемых переменными действия. А посему в одних точках фазового пространства динамической системы резонанс может существовать, а в других – нет. Резонансы соответствуют рациональным соотношениям между частотами, классический же результат теории чисел говорит, что мера рациональных чисел по сравнению с мерой иррациональных равна нулю. Это означает, что резонансы встречаются крайне редко. Кроме того, в отсутствие возмущений, как было сказано выше, резонансы приводят к периодическому движению, а в общем случае мы имеем квазипериодическое движение (нерезонансные торы). Резюмируя, можно сказать, что периодические движения – не правило, а исключение.

(Интересно было бы предположить, какими путями развивалась бы эволюция жизни на Земле, если бы движение Земли вокруг Солнца не носило периодического характера. Возможна ли, например, жизнь в условиях планетной системы двойной звезды? Авторы реферата полагают, что если "крайние" условия, в которые попадала бы такая планета, не были слишком уж жёсткими, то жизнь нашла бы возможность приспособиться и эволюция была бы всё-таки возможна. Однако все эти рассуждения основаны лишь на оптимизме автора и его вере в глубокую приспособляемость всего живого к внешним условиям, и имеют крайне мало отношения к объявленной в заглавии теме работы).

При введении возмущений характер движения на резонансных торах резко изменяется (по теореме Пуанкаре), в то время как квазипериодическое движение изменяется незначительно, по крайней мере, при малом параметре возмущения l. Основной результат теории КАМ состоит в том, что теперь мы имеем два совершенно различных типа траекторий: слегка изменившиеся квазипериодические траектории и стохастические траектории, возникшие при разрушении резонансных торов. Появление стохастических траекторий подтверждается численными экспериментами [1, c.127].

Теория КАМ не приводит к динамической теории хаоса. Её главный вклад в другом: она показала, что при малых значениях параметра l мы имеем промежуточный режим, в котором сосуществуют траектории двух типов – регулярные и стохастические. В дальнейшем нас будет в основном интересовать то, что происходит в предельном случае, когда снова останется только один тип траекторий. Эта ситуация соответствует так называемым большим системам Пуанкаре (БСП), к рассмотрению которых мы и переходим.

При рассмотрении предложенной Пуанкаре классификации динамических систем на интегрируемые и неинтегрируемы мы отметили, что резонансы встречаются редко. При переходе к БСП ситуация радикально изменяется: в БСП резонансы играют главную роль.

Рассмотрим в качестве примера взаимодействие между какой-нибудь частицей и полем. Поле можно рассматривать как суперпозицию осцилляторов с континуумом частот. В отличие от поля, частица совершает колебания с одной фиксированной частотой w₁. Перед нами – пример неинтегрируемой системы Пуанкаре. Резонансы будут возникать всякий раз, когда w₁=w_k. Испускание излучения обусловлено именно такими резонансными взаимодействиями между заряженной частицей и полем. Испускание излучения представляет собой необратимый процесс, связанный с резонансами Пуанкаре.

Новая особенность состоит в том, что частота w_k есть непрерывная функция  индекса k, соответствующая длинам волн осциллятора поля. Такова специфическая особенность больших систем Пуанкаре, то есть хаотических систем, у которых нет регулярных траекторий, сосуществующих с хаотическими траекториями. БСП соответствуют в действительности большинству физических ситуаций, с которыми мы сталкиваемся в природе. Но БСП позволяют также исключить расходимости Пуанкаре, то есть устранить основное препятствие на пути к интегрированию уравнений движения. Этот результат, заметно приумножающий мощь динамического описания, разрушает отождествление ньютоновской или гамильтоновой механики и обратимого по времени детерминизма в духе Лапласа. Уравнения для больших систем Пуанкаре в общем случае приводят к принципиально вероятностной эволюции с нарушенной симметрией во времени. Более подробно вопросы необратимости времени рассмотрим в следующем разделе.

Статистическое описание. Диссипативный хаос

Можно описывать мир в терминах траекторий (в классической физике) или волновых функций (в квантовой механике). Почти сто лет назад Гиббс и Эйнштейн ввели ещё один тип описания – статистическое описание в терминах ансамблей. Описание отдельной динамической системы заменяется описанием ансамбля систем, которые все соответствуют одному и тому же гамильтониану и различаются только начальными условиями эволюции. Для введения ансамблевой точки зрения были две основные причины. Во-первых, описание в терминах ансамбля позволило удобно вычислять средние значения. Во-вторых, понятие ансамбля стало необходимым для описания системы, достигшей термодинамического равновесия. Оказалось, что термодинамические свойства можно понять только в терминах ансамблей, но отнюдь не в терминах отдельных траекторий или волновых функций. Ансамблевый подход применим ко всем динамическим системам, интегрируемым и неинтегрируемым, устойчивым и неустойчивым.

Основной величиной в ансамблевом подходе становится распределение вероятностей. Однако ничто не мешает вернуться как к предельному случаю. Подход Гиббса–Эйнштейна – альтернативный, но эквивалентный способ представления законов физики, он является сводимым статистическим описанием.

Концепцию несводимых статистических описаний, развиваемую школой И.Пригожина, мы подробнее рассмотрим в третьем разделе. Пока что вкратце обратимся к классическому диссипативному хаосу, для которого статистическое описание является единственно возможным подходом. Введём также некоторые понятия, необходимые для дальнейших рассуждений о статистическом описании. (Подробнее – см. [4]).

Как и прежде, каждому состоянию системы соответствует точка в фазовом пространстве. Но в теории ансамблей Гиббса система как целое представима лишь "облаком" точек в фазовом пространстве. Это "облако"  описывается непрерывным распределением плотности вероятности r(q₁,...,q_s,p₁,...,p_s) в фазовом пространстве. Каждая точка фазового пространства движется во времени по своей динамической траектории, которые никогда не пересекаются. Две первоначально различные точки навсегда остаются различными. Это фундаментальное свойство приводит к теореме Лиувилля, которая уже упоминалась при описании преобразования пекаря. Эта теорема утверждает, что плотность r ведёт себя как несжимаемая жидкость: для любой динамической системы объём области, занятой представляющими точками в фазовом пространстве, сохраняется в ходе эволюции. Однако теорема Лиувилля отнюдь не исключает изменения формы области, занятой представляющими точками.

Вернёмся к хаосу. Примеры хаотически ведущих себя динамических систем, описанные выше, относительно новы и, как уже упоминалось, не всегда "физичны". Термодинамика же и статистическая физика примерно на сто лет раньше столкнулись с проблемой хаотического поведения систем.

За примерами далеко ходить не следует – окружающая нас атмосфера ведёт себя вполне хаотически, предсказание прогноза погоды на сколько-нибудь большой срок – задача огромной сложности (хотя в принципе и небезнадёжная).

Однако даже в атмосфере встречаются относительно устойчивые образования и на некотором уровне описания поведение атмосферы не совсем хаотично. Другим примером того, что (термодинамический) хаос и беспорядок – в физике не синонимы, являются широко известные ячейки Бенара (настолько известные, что автор почему-то совершенно не желает в очередной раз давать описание этого явления – см., например, [1, с.68]). И ячейки Бенара, и атмосферные вихри, и многие другие подобные явления относятся к так называемым диссипативным структурам – структурам, существование которых напрямую обусловлено наличием в системе процессов диссипации энергии и производства энтропии.

Образование и эволюция звезд

Существуют две основные концепции происхождения небесных тел. Первая основывается на небулярной модели образования Солнечной системы, выдвинутой еще французским физиком и математиком Пьером Лапласом и развитой немецким философом Иммануилом Кантом. В соответствии с нею звезды и планеты образовались из рассеянного диффузного вещества (космической пыли) путем постепенного сжатия первоначальной туманности.

Принятие модели Большого Взрыва и расширяющейся Вселенной существенным образом повлияло и на модели образования небесных тел и привело к гипотезе Виктора Амбарцумяна о возникновении галактик, звезд и планетных систем из сверхплотного (состоящего из самых тяжелых элементарных частиц — гиперонов) дозвездного вещества, находящегося в ядрах галактик, путем его фрагментации.

Интерпретация небесных тел определяется тем, какую из двух гипотез считают истинной. Открытие В. Амбарцумяном звездных ассоциаций, состоящих из очень молодых звезд, стремящихся убежать друг от друга, было понято им как подтверждение гипотезы образования звезд из первоначального сверхплотного вещества. Какая из двух концепций ближе к истине, решит последующее развитие естествознания.

Модель расширяющейся Вселенной встретилась с несколькими трудностями, которые способствовали прогрессу астрономии. Разлетаясь после Большого Взрыва из точки с бесконечно большой плотностью, сгустки вещества должны слегка притормаживать друг друга силами взаимного притяжения, и скорость их должна падать. Но для торможения не хватает всей массы Вселенной. Из этого возражения родилась в 1939 году гипотеза о наличии во Вселенной так называемых «черных дыр», которые невозможно увидеть, но которые хранят 9/10 массы Вселенной (т. е. столько, сколько недостает).

Что представляют собой «черные дыры»? Если некоторая масса вещества оказывается в сравнительно небольшом объеме, критическом для данной массы, то под действием собственного тяготения такое вещество начинает неудержимо сжиматься. Происходит гравитационный коллапс. В результате сжатия растет концентрация массы и наступает момент, когда сила тяготения на поверхности становится столь велика, что для ее преодоления надо было бы развить скорость большую, чем скорость света. Поэтому «черная дыра» ничего не выпускает наружу и не отражает, и стало быть ее невозможно обнаружить. В «черной дыре» пространство искривляется, а время замедляется. Если сжатие продолжается дальше, тогда на каком-то его этапе начинаются незатухающие ядерные реакции. Сжатие прекращается, а затем происходит антиколлапсионный взрыв, и «черная дыра» превращается в «белую дыру». Предположено, что «черные дыры» находятся в ядрах галактик, являясь сверхмощным источником энергии.

Все небесные тела можно разделить на испускающие энергию — звезды, и не испускающие — планеты, кометы, метеориты, космическую пыль. Энергия звезд генерируется в их недрах ядерными процессами при температурах, достигающих десятки миллионов градусов, что сопровождается выделением особых частиц огромной проницающей способности — нейтрино.

Звезды — это фабрики по производству химических элементов и источники света и жизни. Тем самым решаются сразу несколько задач. Звезды движутся вокруг центра галактики по сложным орбитам. Могут быть звезды, у которых меняются блеск и спектр — переменные звезды (Тау Кита) и нестационарные (молодые) звезды, а также звездные ассоциации, возраст которых не превышает 10 млн. лет. Возможно из них образуются сверхновые звезды, при вспышках которых происходит выделение огромного количества энергии нетеплового происхождения и образование туманностей (скоплений газов).

Существуют очень крупные звезды — красные гиганты и сверхгиганты, и нейтронные звезды, масса которых близка к массе Солнца, но радиус составляет 1/50000 от солнечного (10-20 км); они называются так, потому что состоят из огромного сгустка нейтронов).

В 1967 году были открыты пульсары — космические источники радио-, оптического, рентгеновского и гамма-излучения, приходящие на Землю в виде периодически повторяющихся всплесков. У радиопульсаров (быстро вращающихся нейтронных звезд) периоды импульсов — 0,03-4 сек, у рентгеновских пульсаров (двойных звезд, где к нейтронной звезде перетекает вещество от второй, обычной звезды) периоды составляют несколько секунд и более.

К интересным небесным телам, которым часто приписывалось сверхъестественное значение, относятся кометы. Под воздействием солнечного излучения из ядра кометы выделяются газы, образующие обширную голову кометы. Воздействие солнечного излучения и солнечного ветра обусловливает образование хвоста, иногда достигающего миллионов километров в длину. Выделяемые газы уходят в космическое пространство, вследствие чего при каждом приближении к Солнцу комета теряет значительную часть своей массы. В связи с этим кометы живут относительно недолго (тысячелетия и столетия).

Небо только кажется спокойным. В нем постоянно происходят катастрофы и рождаются новые и сверхновые звезды, во время вспышек которых светимость звезды возрастает в сотни тысяч раз. Эти взрывы характеризуют галактический пульс.

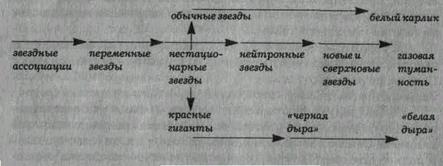
В конце эволюционного цикла, когда все водородное горючее истрачено, звезда сжимается до бесконечной плотности (масса остается прежней). Обычная звезда превращается в «белого карлика» — звезду, имеющую относительно высокую поверхностную температуру (от 7000 до 30000° С) и низкую светимость, во много раз меньшую светимости Солнца.

Предполагается, что одной из стадий эволюции нейтронных звезд является образование новой и сверхновой звезды, когда она увеличивается в объеме, сбрасывает свою газовую оболочку и в течение нескольких суток выделяет энергию, светя как миллиарды солнц. Затем, исчерпав ресурсы, звезда тускнеет, а на месте вспышки остается газовая туманность.

Если звезда имела сверхкрупные размеры, то в конце ее эволюции частицы и лучи, едва покинув поверхность, тут же падают обратно из-за сил гравитации, т.е. образуется «черная дыра», переходящая затем в «белую дыру».

Процесс эволюции звезд представлен на схеме: