Контрольная работа
По дисциплине «Финансовая математика»
Вариант№2
Исполнитель:
Факультет : Ф и К
Курс: 4
№ л/д
№ группы:
Преподаватель: А.И. Пилипенко
Задание №1
Ниже приведены поквартальные данные о кредитах от
коммерческого банка на жилищное строительство (в условных единицах) за 4 года
(всего 16 кварталов).
Таблица 1.
|
квартал
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
|
Кредит от коммерческого
банка на жилищное строительство
|
30
|
38
|
45
|
30
|
32
|
42
|
51
|
31
|
36
|
46
|
55
|
34
|
41
|
50
|
60
|
37
|
Требуется:
1)
Построить
адаптивную мультипликативную модель Хольта-Уинтерса с учетом сезонного фактора,
приняв параметры сглаживания α1=0,3;α2=0,6;
α3=0,3.
2)
Оценить
точность построенной модели с использованием средней относительной ошибки
аппроксимации.
3)
Оценить
адекватность построенной модели на основе исследования:
- случайности
остаточной компоненты по критерию пиков;
-
независимости уровней ряда остатков по d-критерию (критические значения d1=1,10 и d2=1,37) и
по первому коэффициенту автокорреляции при критическом значении r1=0,32;
-
нормальности распределения остаточной компоненты по R/S-критерию с
критическими значениями от 3 до 4,21.
4) Построить
точечный прогноз на 4 шага вперед, т.е. на 1 год.
5) Отразить
на графике фактические, расчетные и прогнозные данные.
Решение:
1.
Мультипликативная модель Хольта-Уинтерса с линейным
ростом имеет следующий вид:
Yp(t+k)=[a(t)
+ k*b(t)] * F( t+k-L),
коэффициенты
модели a(t), b(t) и F(t) рассчитываются по формулам:
a(t)= α1 *Y(t) / F(t-L) + (1- α1 )*[a(t-1)+b(t-1)];
b(t)= α3 * [a(t)-a(t-1)]+(1- α3)*b(t-1);
F(t)= α2 * Y(t)/a(t) + (1- α2)*F(t-L).
Для расчета a(1) и b(1) необходимо
оценить значения этих коэффициентов для предыдущего периода времени. Для оценки
начальных значений a(0) и b(0) применим линейную модель к первым 8 значениям Y(t) из табл.1.
Линейная модель имеет вид:
Yp(t)=a(0) + b(0)*t.
Таблица 2
Промежуточные
расчеты для вычисления коэффициентов
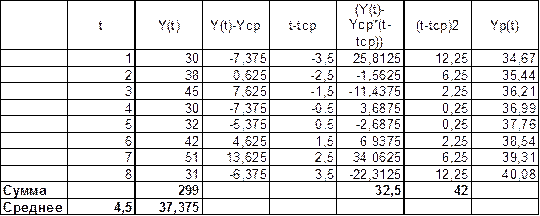
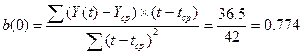
a(0) = Yср – b(0)*tср = 37,375 - 0,774*4,5=33,89
Уравнение с учетом полученных коэффициентов имеет вид:
Yp(t)= 33,89+0,774t
Из этого уравнения находим расчетные значения Yp(t) и
сопоставляем их с фактическими значениями (табл.3)
Таблица 3
Сопоставление фактических данных Y(t) и
рассчитанных по линейной модели значений Yp(t)
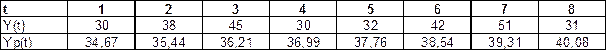
Оценим приближенные значения
коэффициентов сезонности I-IV кварталов
F(-3), F(-2), F(-1) и F(0) для года,
предшествующего первому году, по которому имеются данные в табл.1. Эти значения
необходимы для расчета коэффициентов сезонности первого года F(1), F(2), F(3), F(4) и других
параметров модели Хольта-Уинтерса.
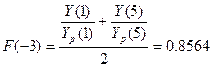 ;
;
 ;
;
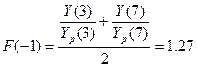 ;
;
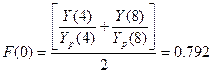 .
.
Оценив значения a(0), b(0), а также F(-3), F(-2), F(-1), F(0), можно
перейти к построению адаптивной мультипликативной модели Хольта-Уинтерса.
Рассчитаем
значения Yp(t), a(t), b(t) и F(t) для t=1.
Полагая,
что t=0, k=1, находим Yp(1):
Yp(0+1)=Yp(1)=[a(0)+1*(b)]*F(0+1-4)=29,69
Полагая
что t=1, находим :
a(1)= α1*Y(1)/F(-3)+(1-α1)*[a(0)+b(0)]=34,78
b(1)= α3*[a(1)-a(0)]+(1-α3)*b(0)=0,806
F(1)= α2*Y(1)/a(1)+(1- α2)*F(-3)=0,860
Аналогично рассчитаем для t=1
Yp(2)=38,47
a(2)= 35,45
b(2)= 0,77
F(2)=1,07
Для t=2:
Yp(3)=46,00
a(3)=35,98
b(3)= 0,696
F(3)= 1,258
Для t=3:
Yp(4)=29,06
a(4)=37,04
b(4)= 0,803
F(4)= 0,802
Для t=4:
Yp(5)=32,55
a(5)= 37,65
b(5)=0,746
F(5)=0,854
Для t=5:
Yp(6)=41,29
a(6)=38,59
b(6)=0,805
F(6)=1,083
Для t=6:
Yp(7)=49,57
a(7)=39,74
b(7)=0,907
F(7)=1,273
Для t=7:
Yp(8)=32,63
a(8)=40,03
b(8)=0,724
F(8)=0,785
Для t=8:
Yp(9)=34,81
a(9)=41,18
b(9)=0,849
F(9)=0,866
Для t=9:
Yp(10)=45,52
a(10)=42,16
b(10)=0,889
F(10)=1,09
Для t=10
Yp(11)=54,82
a(11)=43,09
b(11)=0,902
F(11)=1,275
Для t=11:
Yp(12)=34,56
a(12)=43,77
b(12)= 0,837
F(12)=0,780
Для t=12:
Yp(13)=38,64
a(13)=45,42
b(13)=1,082
F(13)=0,887
Для t=13:
Yp(14)=50,60
a(14)=46,34
b(14)=1,032
F(14)=1,082
Для t=14:
Yp(15)=60,42
a(15)=47,28
b(15)=1,002
F(15)=1,271
Для t=15:
Yp(16)=37,68
a(16)=48,02
b(16)=0,924
F(16)= 0,774
Таблица 4

2.
Проверка точности модели
Условие точности выполняется, если
относительная погрешность в среднем не превышает 5%. Суммарное значение относительных погрешностей (см.табл.4)
составляет 34,89, что дает среднюю величину 34,89/16=2,18%.
Следовательно, условие точности выполнено.
3.
Проверка условия адекватности.
Проверка
случайности уровней. Проверку
случайности уровней остаточной компоненты проводим на основе критерия
поворотных точек. (табл.5)
Таблица 5
Промежуточные расчеты для оценки адекватности
модели
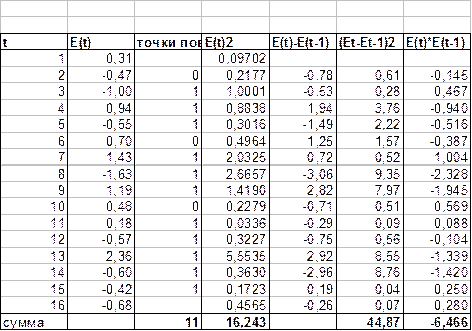
Общее число поворотных точек в нашем
примере равно p=11
Рассчитаем значение q:
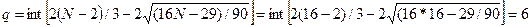
Если количество поворотных точек p больше
q, то условие случайности уровней выполнено. В нашем
случае p=11, q=6, значит
условие случайности уровней ряда выполнено.
Проверка
независимости уровней ряда остатков.
а) по d-критерию Дарбина-Уотсона
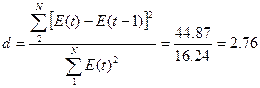
В нашем случае имеет место отрицательная
автокорреляция. В таком случае величину d уточняем,
вычитая полученное значение из 4.
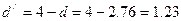
d1<1.23
<d2, Критерий
Дарбина-Уотсона не дает ответа на вопрос о независимости уровней ряда остатков.
б) по первому коэффициенту
автокорреляции
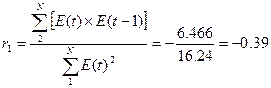
Если модуль рассчитанного значения
первого коэффициента автокорреляции меньше критического значения r(1) < r табл , то уровни ряда остатков независимы. В нашей задаче /r(1)/=0,39>rтаб=0,32 – условие независимости не выполняется
Проверка
соответствия ряда остатков нормальному распределению определяем по RS –критерию. Рассчитаем значение RS:
RS=(Emax – Emin)/S,
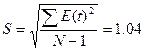
RS= (2,36-(-1.43))/1,04=3,83
Так как 3,00<3,83<4,21, полученное
значение RS попало в
заданный интервал, то уровни ряда остатков подчиняются нормальному распределению.
4.
Построение
точечного прогноза
Для
t=17 имеем:
Yp(17)=Yp(16+1)=[a(16)+b(16)]*F(16+1-4)= (48.02+0.924)*0.887=43.41
Аналогично
находим Yp(18), Yp(19),
Yp(20):
Yp(18)=Yp(16+2)=(48.02+2*0.924)*1.082=53.96
Yp(19)=( 48.02+3*0.924)*1.271=64.56
Yp(20)=( 48.02+4*0.924)*0.774=40.02
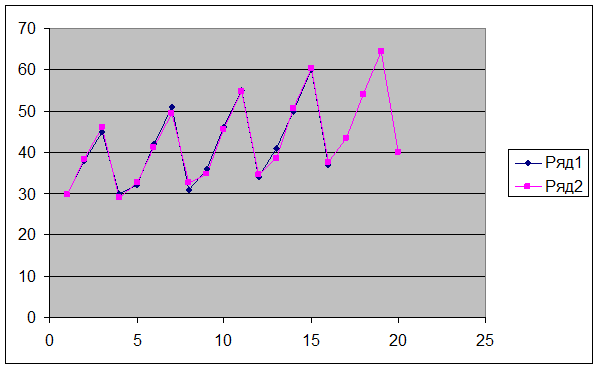
5.
Отражение на графике
фактических, расчетных и прогнозных данных
Задание № 2.
Даны цены (открытия, максимальная,
минимальная и закрытия) за 10 дней. Интервал сглаживания принять равным пяти
дням. Рассчитать:
- экспоненциальную скользящую среднюю;
- момент;
- скорость изменения цен;
- индекс относительной силы;
- %R, %K, %D.
Расчеты проводить для всех дней, для
которых эти расчеты можно выполнить на основании имеющихся данных.
|
дни
|
Макс.
|
Мин.
|
Закр.
|
|
1
|
765
|
685
|
750
|
|
2
|
792
|
703
|
733
|
|
3
|
740
|
706
|
733
|
|
4
|
718
|
641
|
666
|
|
5
|
680
|
600
|
640
|
|
6
|
693
|
638
|
676
|
|
7
|
655
|
500
|
654
|
|
8
|
695
|
630
|
655
|
|
9
|
700
|
640
|
693
|
|
10
|
755
|
686
|
750
|
Решение:
Результаты расчетов см. в таблице 6 и 7.
1.
Экспоненциальная
скользящая средняя.
EMAt=k*Ct+(1-k)*EMAt-1,
где k=2/(n+1)
Ct – цена закрытия t-го дня
2.
Момент
MOMt=Ct
– Ct-n
Положительные значения МОМ свидетельствуют об
относительном росте цен, отрицательные – о снижении
3.
Скорость
изменения цен
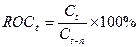
ROC является
отражением скорости изменения цены, а также указывает направление этого
изменения.
4.
Индекс
относительной силы
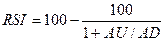 ,
,
где AU –
сумма приростов конечных цен за n последних дней;
AD – сумма убыли конечных цен за n последних дней.
5.
Стохастические
линии
%Kt=100*(Ct
– L5)/(H5 – L5);
%Rt=100*(H5
– Ct)/(H5 – L5);
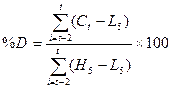 ;
;
где Ct – цена закрытия
текущего дня.
L5 и H5 – минимальная и
максимальная цены за 5 предшествующих дней, включая текущий.
Таблица 6.
Расчет ROC,MOM и RSI
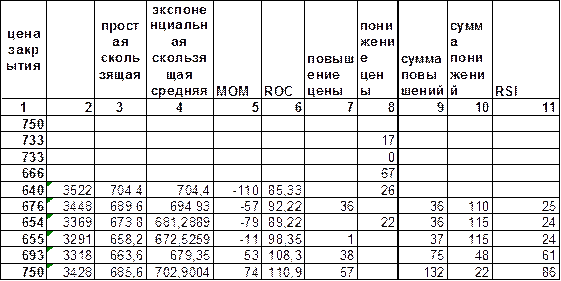
Алгоритм расчета:
1. выберем интервал сглаживания n(в нашем случае n=5)
2. вычислим коэффициент К(К=2/(n+1)=2/6=1/3
3. вычислим MA для
первых 5 дней. Для этого сложим цены закрытия за первые 5 дней(графа 2). Сумму
разделим на 5 и запишем в графы 3 и 4 за 5-й день.
4. перейдем на одну строку вниз по графе 4. Умножим на
К данные по конечной цене, которую берем
из графы 1 текущей строки.(Для 6-го дня это будет 676*1/3=225.33).
5. данные по ЕМА за предыдущий день берем из предыдущей
строки графы 4 и умножаем на (1 - К).(Для 6-го дня это будет 704.4*2/3=469.60)
6. сложим результаты, полученные на предыдущих двух шагах
(для 6-го дня это будет 225.33+469.60=694.93.Полученное значение записываем в
графу 4 текущей строки.
7. повторяем шаги 4, 5 и 6 до конца таблицы.
RSI рассчитывается следующим образом:
1. начиная со 2-го дня до конца таблицы вычитают из
конечной цены текущего дня конечную цену предыдущего дня. Если разность больше
нуля, то ее записывают в графу 7. Иначе абсолютное значение разности записывают
в графу 8.
2. с 6-го дня и до конца таблицы заполняют графы 9 и 10.
для этого складывают значения из графы 7 за последние n дней(включая
текущий) и полученную сумму записывают в графу 9(величина AU). Аналогично находят сумму убыли конечных цен по
данным графы 8 и записывают в графу 10. (величина AD).
3. зная AU и AD, рассчитывают
значение RSI и записывают в графу 11.
Задание №3
Выполнить различные коммерческие
расчеты, используя данные, приведенные в таблице. В условии задачи значения
параметров приведены в виде переменных. По именам переменных из таблицы
необходимо выбрать соответствующие численные значения параметров и выполнить
расчеты.
Таблица 8.
|
вариант
|
сумма
|
Дата начальная
|
Дата конечная
|
Время в днях
|
Время в годах
|
ставка
|
Число начислений
|
|
S
|
Тн
|
Тк
|
Тдн
|
Тлет
|
i
|
m
|
|
4
|
1 000 000
|
18.01.02
|
12.03.02
|
180
|
4
|
15
|
2
|
1.
Банк выдал ссуду,
размером 1 000 000 руб. Дата выдачи ссуды 18.01.02, возврата – 12.03.02. День выдачи и день возврата считать за 1 день.
Проценты рассчитываются по простой процентной ставке 15 % годовых. Найти:
1.1 точные проценты с точным числом дней ссуды;
1.2 обыкновенные проценты с точным числом дней ссуды;
1.3 обыкновенные проценты с приближенным числом дней
ссуды.
Решение:
1.1 По формулам:
S=P+I, где I=Pni
n=t/K
K=365, t=53, I= 1000000*0.15*53/365=21780.82руб.
1.2. К=360, t=53, I=1000000*0.15*53/360=22083.33руб
1.3. K=360, t=55, I= 1000000*0.15*55/360=22916.67руб.
2. Через Тдн
после подписания договора должник уплатит S руб. Кредит выдан под i %
годовых (проценты обыкновенные). Какова первоначальная сумма и дисконт?
Решение:
Используем формулы:
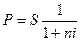 , i-ставка
простых процентов, n – период
, i-ставка
простых процентов, n – период
D=S – P
P=1000000/(1+0.15*180/360)=930232.56руб.
D=1000000 – 930232.56=69767.44руб.
3.
Через Тдн
дней предприятие должно получить по векселю S руб. Банк
приобрел этот вексель с дисконтом. Банк учел вексель по учетной ставке i % годовых (год
равен 360 дням). Определить полученную сумму предприятием и дисконт.
Решение:
Используем формулы:
D=Snd, откуда P=S – D=S – Snd=S(1 - nd)
D=Snd=1000000*0.15*180/360=75000 руб.
P=1000 000 – 75
000=925 000 руб.
4.
В кредитном договоре на сумму S руб. и сроком на Тлет, зафиксирована
ставка сложных процентов, равная i% годовых. Определить наращенную сумму.
Решение:
По формуле: S=P(1+i)n = 1000 000 *(1+0.15)4=1749006.3руб.
5.
Ссуда, размером S руб.
предоставлена на Тлет. Проценты сложные, ставка – i% годовых.
Проценты начисляются m раз в году. Вычислить наращенную сумму.
Решение:
S=1000 000*(1+0.15/2)8=1783477.83руб.
6.
Вычислить
эффективную ставку процента, если банк начисляет проценты m раз в году, исходя из номинальной ставки i% годовых.
Решение:
iэ=(1+j/m)m – 1 = (1+0.15/2)2 – 1=0,155 т.е. 15.5%
7.
Определить, какой
должна быть номинальная ставка при начислении процентов m раз
в году, чтобы обеспечить эффективную ставку i% годовых.
Решение:
j=m[(1+iэ)1/m – 1] = 2[(1+0.15)1/2 – 1]=0,14т.е. 14%
8.
Через Тлет
предприятию будет выплачена сумма S руб.
Определить ее современную стоимость при условии, что применяется сложная
процентная ставка i% годовых.
Решение:
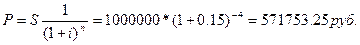
9.
Через Тлет
по векселю должна быть выплачена сумма S руб. Банк учел вексель по сложной учетной ставке i% годовых.
Определить дисконт.
Решение:
P=S(1 – dсл)n=1000000*(1 – 0.15)4=522006.25 руб.
D=S – P=1000000 – 522006.25=477993.75.
10.
В течение Тлет
на расчетный счет в конце каждого года поступает по S руб., на
которые m раз в году
начисляются проценты по сложной годовой ставке i%. Определить сумму на расчетном счете к концу
указанного срока.
Решение:
S=1000000*[(1+0.15/2)(4*2) – 1]/[(1+0.15/2)2
– 1]=5034395.67руб.