Высшая математика

1. Вычислить площадь области, заданной неравенствами:

(х + r)2 + у2 ≤ r2,     у ≥ 0,     2х + 2r ≥ у, перейдя предварительно к полярным координатам.

Решение. Переходим к полярным координатам  по формулам

х + r = ,    у =

Теперь область задаётся неравенствами

0 ≤  ≤ arctg 2,    0 ≤  ≤ r.

Её площадь равна повторному интегралу

.


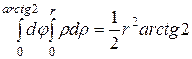2. Вычислить интеграл (в цилиндрических или сферических координатах).

,

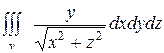где V – область, заданная неравенствами:

х2 + у2 + z2 ≤ 4R2,    х2 + z2 ≤ 2Rх,    у ≥ 0.

Решение. Переходим к цилиндрическим координатам  по формулам

х = ,    z = .

Теперь область V задаётся неравенствами

         

Тройной интеграл равен повторному интегралу

2=


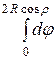
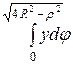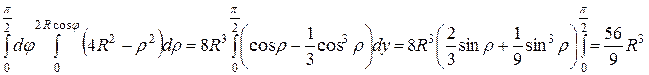
Дискретная математика

Тема: «Основные понятия теории множеств».

1. Пусть R – множество вещественных чисел, х = ,

у = .

Что представляют собой множества  XY,    XY,   X/Y?

Решение. XY = {xR, 0 ≤ x ≤ 2} = Y$

                 XY = {xR, 0 ≤ x ≤ 1} = x,

                 X/Y = X=  О – пустое множество.


2. Пусть Х = {-1, -2, -3, 1, 2, 3, 0} и Y – множество всех натуральных чисел. Каждому числу хХ ставиться в соответствие его квадрат. Выпишите все пары, принадлежащие этому соответствию.

Решение: (-1, 1), (-2, 4), (-3, 9), (1, 1), (2, 4), (3, 9), (0, 0).


3. Определите свойства следующих отношений:

а) «прямая х пересекает прямую у» (на множестве прямых);

б) «число х больше числа у на 2» (на множество натуральных чисел);

в) «число х делится на число у без остатка» (на множестве натуральных чисел);

г) «х – сестра у» (на множестве людей).

Решение. а) антирефлексивно, симметрично, не транзитивно;

                 б) антирефлексивно, антисимметрично, транзитивно;

                 в) рефлексивно, не антирефлексивно, не симметрично, антисимметрично, транзитивно;

                 г) не рефлексивно, антирефлексивно, не симметрично, не антисимметрично, транзитивно.


Тема: «Основы математической логики. Основы теории алгоритмов. Элементы комбинаторного анализа».

1.     Определить, является ли справедливой приведённая формула алгебры высказываний, не прибегая к составлению таблицы истинности, а используя только свойства соответствующих операций.

,

где А, В, С, D, Е – простые высказывания.

Решение. По правилу Моргана получаем

 = .

Нет совпадения с первой частью, так что приведённая формула не является справедливой.


2. Для указанных функций трёх переменных: f (х1, х2, х3) – принимаем единичные значения на наборах № 0, 1, 3, 6, 7.

- составить таблицу истинности;

- определить, к каким классам булевых функций она относится;

- записать совершенные ДНФ и КНФ;

- найти минимальную ДНФ;

- для полученной минимальной ДНФ построить логическую схему в базисах:

а) {, -} (дизъюнкция, отрицание);

б) {, -} (конъюнкция, отрицание).

Решение. Составим таблицу истинности для функции f и двойственной функции f*.

№

х1

х2

х3

f

f*

0

0

0

0

1

0

1

0

0

1

1

0

2

0

1

0

0

1

3

1

0

0

1

1

4

0

1

1

0

0

5

1

0

1

0

1

6

1

1

0

1

0

7

1

1

1

1

0


Функция f не сохраняет 0, сохраняет 1, не является самодвойственной, не является монотонной, не является линейной.

Совершенная ДНФ для функции f имеет вид

Совершенная КНФ для функции f имеет вид

Если отказаться от совершенности ДНФ, то она принимает более простой вид

Полученная минимальная ДНФ допускает два представления:

а)

б) .


3. Является ли полной система булевых функций, состоящая из импликации и отрицания? Доказать полноту (или неполноту) приведённой системы булевых функций, состоящей из импликации и отрицания.

Решение. Булева функция импликации задана следующей таблицей истинности.

х1

х2

f

f*

0

0

1

0

0

1

1

1

1

0

0

0

1

1

1

0

Булева функция отрицания принадлежит классу самодвойственных функций и классу линейных функций, не сохраняет 0 и 1, не является монотонной. Согласно теореме Поста, для импликации остаётся проверить только отсутствие самодвойственности и линейности. Самодвойственности, как показывает таблица истинности, нет. Свойство линейности тоже не удаётся обнаружить. Значит, система полная.


4. Составить программу машины Тьюринга, уменьшающей данное число на единицу.

Решение. Число р должно быть записано в двоичной системе, после последней цифры должен стоять знак # (решётка). Число уменьшится на единицу, если при обратном ходе машины Тьюринга (справа налево) первая попавшаяся единица будет заменена нулём, а все остальные цифры сохранятся. Машину Тьюринга берём в виде пятёрки.

.

Программа Р имеет следующий вид

1

q0

1

q0

1

0

q0

0

q0

1

#

q0

#

q1

-1

0

q1

0

q1

-1

1

q1

0

q2

-1

0

q2

0

q2

-1

1

q2

1

q2

-1

Считаем, что в начальный момент головка смотрит на первый символ слова р в состоянии q0.


5. Из колоды карт, содержащей 52 карты, вынули 10 карт. В скольких случаях окажется, что среди вынутых карт: а) хотя бы один туз; б) ровно один туз.

Решение. Сразу же получаем ответ на вопрос.

б) 4 С(48, 9), где С(n, m) – число сочетаний из n элементов по m.

а) Всего существует С(52, 10) способов вынуть из колоды карт 10 карт, при этом совсем не будет тузов в С(48, 10) случаях. Значит, ответом будет число С(52, 10) – С(48, 10).