Вариант 10
Задача 10.
Оксид трехвалентного элемента содержит 31,58% кислорода.
Вычислите молярную массу эквивалента, молярную и атомную массы этого элемента.
Решение:
Формула оксида Э2О3.
Найдем молярную массу соединения:
48 г/ моль соответствует 31,58% кислорода
х г/моль соответствует 100%
х = 48*100/31,58 = 151,99 г/моль
Молярная масса элемента:
2х + 48 = 151,99
х = 51,99 г/ моль
Данный элемент – хром
Эквивалент хрома равен = 51,99/3 = 17,33
Атомная масса хрома равна молярной массе и равна 51,99
г/моль.
Задача30
Напишите электронные и электронно-графические формулы атомов
элементов с порядковыми номерами 22 и 24. Сколько свободных 3d-орбиталей в
атомах этих элементов.
Решение:
Элемент с порядковым номером 22 – титан.
Электронная формула:
1s22s22p63s23p64s23d2
В Периодической системе Д.И. Менделеева химический элемент
титан расположен в 4 периоде, 4 группе, побочной подгруппе. Ядро атома титана
содержит 22 протона и 26 нейтронов, вокруг ядра расположено 22 электрона.
Электронная формула имеет следующий вид: 1s22s22p63s23p63d24s2, в графическом виде представлена
следующим образом (рис.1).
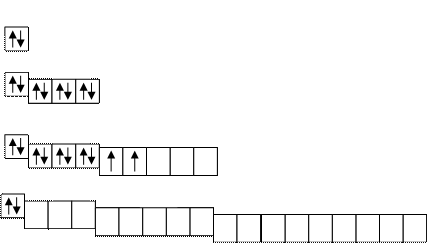 1 (K)
1 (K)
2 (L)
3 (M)
4 (N)
Рисунок 1 - Схема
распределения электронов в нейтральном и невозбужденном атоме титана.
Валентными орбиталями являются орбитали внешней электронной оболочки, находящиеся в самом
нестабильном энергетическом состоянии (максимальная валентность титана равна 9,
то есть числу валентных орбиталей 4s-, 4р- и Зd-подуровней, причём 4 связи могут образовываться по
обменному, а 5 - по донорно-акцепторному
механизму).
Титан относится к d-элементам, является переходным металлом.
В атоме титана 3 свободных d- орбитали.
Первым элементом с явлением проскока электрона является хром
. Рассмотрим подробнее его электронное строение (рис. 2). У атома хрома на 4s-подуровне
не два, как этого следовало бы ожидать, а только один электрон. Зато на 3d-подуровне
пять электронов, а ведь этот подуровень заполняется после 4s-подуровня.
Чтобы понять, почему так происходит, посмотрим, что собой представляют
электронные облака 3d-подуровня этого атома[1].
Каждое из пяти 3d-облаков в этом случае образовано
одним электроном.Общее электронное облако таких пяти
электронов имеет шарообразную форму, или, как говорят, сферически симметрично.
По характеру распределения электронной плотности по разным направлениям оно
похоже на 1s-ЭО. Энергия подуровня, электроны которого образуют такое
облако, оказывается меньше, чем в случае менее симметричного облака. В данном
случае энергия орбиталей 3d-подуровня равна
энергии 4s-орбитали. При нарушении симметрии, например, при появлении
шестого электрона, энергия орбиталей 3d-подуровня
вновь становится больше, чем энергия 4s-орбитали. Поэтому у атома
марганца опять появляется второй электрон на 4s-АО.
Сферической симметрией обладает общее облако любого
подуровня, заполненного электронами как наполовину, так и полностью. Уменьшение
энергии в этих случаях носит общий характер и не зависит от того, наполовину
или полностью заполнен электронами какой-либо подуровень. А раз так, то
следующее нарушение следует искать у атома, в электронную оболочку которого
последним "приходит"девятый d-электрон. И действительно, у
атома меди на 3d-подуровне 10 электронов, а на 4s-подуровне
только один.
Электронно-графическая формула атома хрома приведена на
рис.2
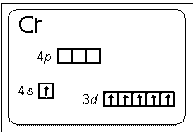
Рисунок 2 - Рисунок 1 - Схема распределения электронов в нейтральном и
невозбужденном атоме хрома.
Таким образом, в атоме хрома нет свободных d-орбиталей,
все d-орбитали заполнены.
Задача 50
Как метод валентных связей (ВС) объясняет угловое строение
молекулы Н2S
и линейное строение молекулы СО2?
Решение:
Геометрическая форма молекул соединений зависит от типа
гибридных орбиталей, участвующих в образовании
ковалентных связей. Гибридным sp-орбиталям отвечает
линейная структура молекул, sp2-гибридизация приводит к образованию
плоских треугольных молекул, при sp3-гибридизации образуются
молекулы тетраэдрической формы, результат гибридизации типа sp3d2
¾
молекулы октаэдрической конфигурации.
В молекуле Н2S sp3-гибридизация (рис.3).
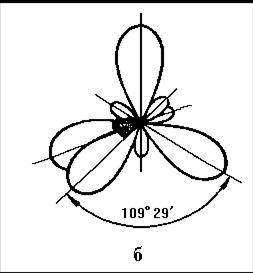
Рисунок 3 - Расположение электронных облаков при sp3-гибридизации
¾
четыре sp3-облака в молекуле Н2S
В молекуле Н2S атом S
образует четыре s-связи
с атомами водорода, при этом осуществляется, sp3-гибридизация орбиталей, и молекула имеет форму тетраэдра.
В молекуле диоксида углерода O=C=O атом углерода образует
две p-связи
с атомами кислорода. В образовании s-связей принимают участие две гибридные sp-орбитали, поэтому молекула CO2 линейна.
Полярные молекулы можно рассматривать как электрические
диполи, в которых разные по знаку, но одинаковые по величине заряды расположены
на определенном расстоянии друг от друга. Мерой полярности молекул служит
дипольный момент, представляющий собой произведение величины заряда на
расстояние между центрами положительного и отрицательного зарядов в молекуле.
Наличие или отсутствие дипольного момента у молекулы часто позволяет судить о
её геометрическом строении. Например, для молекулы типа AB2 возможно
линейное или угловое строение (рис. 4):
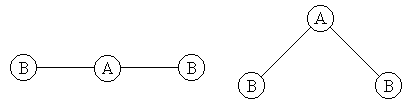
Рисунок 4 – Строение молекул Н2S и
CO2
Линейная структура характеризуется симметричным
распределением зарядов и отвечает неполярной молекуле. Напротив, в молекуле,
имеющей угловое строение, заряды распределяются асимметрично. Такая молекула полярна. Из того факта, что молекула CO2 неполярна, а молекула Н2S обладает дипольным моментом, можно
сделать вывод о линейном строении молекулы диоксида углерода и угловом строении
молекулы сероводорода.
Задача 70
Тепловой эффект реакции сгорания жидкого бензина с
образованием паров воды и диоксида углерода равен – 3135,58 кДж. Составьте
термохимическое уравнение этой реакции и вычислите теплоту образования С6Н6
(ж).
Решение:
С6Н6 (ж) + 7 ½О2
(г)=6СО2 (г)+ 3Н2О (г)– 3135,58 кДж
Тепловой эффект данной реакции выражается уравнением:
∆Нr
= 3∆Нº( Н2О) + 6∆Нº( СО2) -7 ½ ∆Нº( О2) - ∆Нº(
С6Н6)
Откуда
∆Нº( С6Н6)
= 3∆Нº( Н2О) + 6∆Нº( СО2) - 7 ½ ∆Нº( О2) - ∆Нr
∆Нº( Н2О) =
-241,81 кДж
∆Нº( СО2) =
-393,51 кДж
∆Нº( О2) = 0
∆Нº( С6Н6)
= 3 * (-241,81) + 6 * (-393,51) – 0 – (-3135,58) = -725,43 – 2351,06 + 3135,58
= 59,09 кДж
Задача 90
Не производя вычислений установить знак ∆Sº
следующих процессов:
а) 2 NH3
(г) = N2 (г) + 3Н2 (г)
б) СО2 (к) = СО2 (г)
в) 2NO (г) + О2 (г) = 2NO2 (г)
Решение:
Согласно второму закону термодинамики в замкнутой
макроскопической системе энтропия при любом реальном процессе либо возрастает,
либо остается неизменной, но никогда самопроизвольно не уменьшается:
∆S
≥0
При переходе газа (самого беспорядочного состояния вещества
из-за хаотического движения частиц) в жидкость и далее жидкости в твердое
состояние упорядоченность системы возрастает, а ее энтропия уменьшается.
Таким образом, в первом рассматриваемом процессе энтропия
положительна, во втором – положительна, в третьем процессе энтропия также
положительна.
Задача 110
Во сколько раз увеличится скорость реакции, протекающей при
298 К, если ее энергию активации уменьшить на 4 кДж/моль?
Решение:
Почти все химические реакции при повышении температуры идут
быстрее. Зависимость скорости реакции от температуры описывается уравнением
Аррениуса:
k = Ae–Ea/RT,
где k – константа
скорости реакции, А – не зависящая от температуры константа (ее
называют предэкспоненциальным множителем), Еа – энергия активации, R –
газовая постоянная, Т – абсолютная температура
Зависимость скорости реакции от температуры определяют в
соответствии с так называемым «правилом Вант-Гоффа».
Это чисто эмпирическое правило, т.е. правило, основанное не на теории, а
выведенное из опытных данных. В соответствии с этим правилом, повышение
температуры на 10° приводит к увеличению скорости в 2–4 раза.
Математически эту зависимость можно выразить уравнением v2 /v1
= g (T2
– T1)/10, где v1 и v2
– скорости реакции при температурах Т1 и Т2;
величина g называется температурным
коэффициентом реакции. Например, если g
= 2, то при Т2 – Т1 = 50о
v2/v1 = 25 = 32, т.е. реакция
ускорилась в 32 раза, причем это ускорение никак не зависит от абсолютных
величин Т1 и Т2, а только от их разности.
Однако из уравнения Аррениуса следует, что температурный
коэффициент реакции зависит как от энергии активации, так и от абсолютной
температуры. Для данной реакции с определенным значением Еа
ускорение при повышении температуры на 10° будет тем больше, чем ниже
температура. Это почти очевидно и без расчетов: повышение температуры от 0 до
10° С должно сказаться на скорости реакции значительно сильнее, чем такое же
повышение температуры, например, от 500 до 510° С.
С другой стороны, для данного температурного интервала
ускорение реакции будет тем сильнее, чем больше ее энергия активации. Так, если
энергия активации реакции мала, то такая реакция идет очень быстро, и при
повышении температуры на 10° С ее скорость почти не изменяется. Для таких
реакций температурный коэффициент намного меньше 2. Для реакций же с большой
энергией активации, которые при невысоких температурах идут медленно, ускорение
при повышении температуры на 10° С может значительно превысить 4-кратное.
Если в выражении для правила Вант-Гоффа
подставить вместо скоростей v1 и v2 для
данной реакции их зависимости от температуры, в соответствии с уравнением
Аррениуса, то после сокращения предэкспоненциальных
множителей получим следующее выражение: g
= vT +10/vT = е–Еа/R(Т+10)/е–Еа/RТ
= е(Еа/R)[1/Т – 1/(T+10)].
Логарифмирование
этого уравнения дает:
lng = (Eа/R)[1/T – 1/(T +
10)], откуда Еа = Rlng T(T + 10)/10 = 0,83lngT(T + 10). Энергия активации
не является функцией температуры, эта зависимость нужна лишь для удобства
последующего анализа. Последнее уравнение – это уравнение параболы, в
котором физический смысл имеют только положительные значения. Соответствующая
диаграмма ограничена двумя ветвями параболы: при g
= 2 получаем Еа = 0,58Т(Т
+ 10), при g = 4 получаем Еа = 1,16Т(Т + 10). К тем
же формулам приходим и при использовании десятичных логарифмов. Соответствующие
графики двух парабол, для значений g 2
и 4, приведены на рисунке. Их физический смысл заключается в том, что области
выполнения правила Вант-Гоффа соответствует только
область между параболами. Таким образом, существуют только определенные
соотношения между энергией активации реакции и температурой ее проведения, при
которых правило Вант-Гоффа выполняется. Ниже нижней
ветви температурный коэффициент g <
2, тогда как выше верхней ветви g >
4.
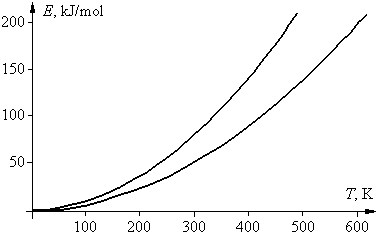
Рисунок 5 – Зависимость энергии активации от
температуры
Если посмотреть, какие реакции «укладываются» в указанную
довольно узкую область, то окажется, что все эти реакции идут не слишком быстро
и не слишком медленно, а с удобной для измерения (при данной температуре)
скоростью.
По рис. 5 находим Еа ~
75 кДж.
Тогда g = vT +10/vT = е–Еа/R(Т+10)/е–Еа/RТ
= е(Еа/R)[1/Т – 1/(T+10)]
= 2,7375/8,134(1/298 – 1/308) = 5
Задача 130
В какой массе воды надо растворить 67,2 л HCl
(объем измерен при нормальных условиях), чтобы получить 9%-ый (по массе)
раствор HCl?
Решение:
1. Найдем количество вещества HCl:
n = V/Vm, где Vm
– молярный объем газа, при нормальных условиях равен 22,4 л
n = 67,2/22,4 = 3 моль
2. Найдем массу HCl:
36,5 * 3 = 109,5 г
3. Найдем массу раствора HCl:
ω = m (HCl)/ m (раствора) * 100
m (раствора)
= m (HCl)
* 100 / ω
m (раствора)
= 109,5 * 100/ 9 = 1216,66 г
Т.к. масса раствора включает массу вещества и массу воды, то
масса воды равна разности между массой раствора и массой HCl:
Масса воды равна:
1216,66 – 109,5 = 1107,16 г
Задача 150
В каком объеме должны быть растворены 10 г этилового спирта C2Н5ОН,
чтобы осмотическое давление раствора при 15º С составило 104
Па?
Решение:
Согласно закону Вант-Гоффа, осмотическое
давление раствора численно равно тому газовому давлению, которое имело бы
растворенное вещество, будучи переведенным в газообразное состояние в том же
объеме и при той же температуре. Поскольку объем (разбавление) обратно
пропорционален концентрации, то закон Вант-Гоффа
можно записать в виде
π = С* R* Т
Измерение осмотического давления раствора используется для
определения молекулярных масс даже разбавленных растворов, что позволяет
оценивать молекулярные массы растворимых высокомолекулярных соединений, в
частности, биополимеров. Заменив C(B) в формуле Вант-Гоффа
соотношением (m(B) ∙ 1000 / μ(B) ∙ V), получим
уравнение, позволяющее вычислять молекулярные массы растворенных веществ:
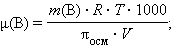
m(B) – масса растворенного вещества, V – объем
раствора.
V = m(B) *
R * T * 1000 / μ(B) π
V = m(B) *
R * T * 1000 / μ(B) π = 10 * 8,314 * 288 * 1000 / 46*104 =
52,05 л
Задача 170
Составьте ионно-молекулярные и молекулярные уравнения
гидролиза солей CuCl2, Cs2CO3,
Cr(NO3)3. Какое
значение рН (7<pH<7) имеют растворы этих солей?
Решение:
Гидролиз CuCl2:
Хлорид меди – соль, образованная слабым основанием и сильной
кислотой.
CuCl2 + Н2О ↔
Сu2+
+ Н2О → СuОН+
+ Н+
CuCl2 + Н2О ↔ СuОНСl + НСl
Гидролиз протекает по первой ступени.
Среда раствора кислая, рН < 7.
Гидролиз Cs2CO3:
Карбонат цезия – соль, образованная сильным основанием и
слабой кислоты
Cs2CO3 + Н2О
→
CO32-
+ Н2О → НСО3- + ОН-
Cs2CO3 + Н2О
→ СsНСО3 + Сs ОН
Среда раствора щелочная, рН > 7
Гидролиз Cr
(NO3)3:
Cr (NO3)3 –
соль, образованная слабым основанием и сильной кислотой.
Гидролиз преимущественно протекает по двум ступеням.
Cr3+
+ Н2О → CrОН2+
+ Н+
Cr (NO3)3
+ Н2О → CrОН (NO3)2 + НNO3
CrОН2+
+ Н2О → Cr(ОН)2+
+ H+
CrОН(NO3)2 +
Н2О → Cr(ОН)2NO3 + HNO3
В растворе образуются преимущественно катионы водорода,
среда кислая, рН<7.
Задача 190
Реакции выражаются схемами:
KClO3
+ Na2SO3 → KCl + Na2SO4
KMnO4 + HBr → Br2
+ MnBr2 + H2O
Составьте электронные уравнения. Расставьте коэффициенты в
уравнениях реакций. Для каждой реакции укажите, какое вещество является
окислителем, какое восстановителем, какое окисляется, какое восстанавливается.
Решение:
+5 +4 -1 +6
KClO3
+ Na2SO3 → KCl + Na2SO4
Сl +5 + 6e → Cl-1|
1| восстановление, окислитель
S+4 - 2e → S+6 | 3 |
окисление, восстановитель
Сl +5
+ 3 S+4 → Cl-1
+ 3 S+6
KClO3
+ 3 Na2SO3 →
KCl + 3 Na2SO4
+7
-1 0 +2
KMnO4 + HBr → Br2
+ MnBr2 + H2O + КBr
Mn7+ + 5е → Mn2+ | 2 | восстановление, окислитель
2Br-
-2е → Br2 |5 | окисление,
восстановитель
2Mn7+ + 10Br- → 2Mn2+ + 5Br2
2KMnO4 + 16HBr
→ 5Br2
+ 2MnBr2
+ 8H2O + 2КBr
Задача 210
Какой гальванический элемент называют концентрационным? СОставльте схему, напишите электронные уравнения
электродных процессов и вычислите ЭДС гальванического элемента, состоящего из
серебряных электродов, опущенных: первый в 0,01 н, а
второй в 0,1 н растворы AgNO3.
Решение:
Зависимость потенциала от концентрации ионов соли в растворе
выражается формулой Нернста.
Если ЭДС элемента положительна, то реакция (так, как она
записана в элементе) протекает самопроизвольно. Если ЭДС отрицательна, то
самопроизвольно протекает обратная реакция.
Разность потенциалов гальванической цепи можно получить,
соединяя два металла, обладающие различной степенью растворения и погруженные в
растворы, содержащие одноименные с ними ионы. Можно также соединить электроды
из одного и того же металла, но погруженные в растворы с неодинаковой
концентрацией ионов α1 и α2, где α2>α1.
В последнем случае ЭДС цепи будет равна:

Такая цепь называется концентрационной. Зная концентрацию
ионов в одном из растворов и измерив ЭДС гальванического элемента, находят
концентрацию ионов в другом растворе. На этом основан один из методов
определения концентрации водородных ионов.
ЭДС элемента связана с ΔG
протекающей в элементе реакции:
ΔG = - nFE
Зная стандартную ЭДС, можно рассчитать константу равновесия
протекающей в элементе реакции:
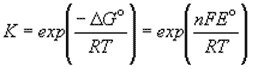
Константа равновесия реакции, протекающей в элементе
Даниэля-Якоби при нормальных условиях, равна:
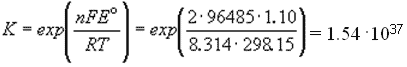
Зная температурный коэффициент ЭДС 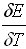 для
гальванического элемента можно рассчитать и некоторые термодинамические
функции, например:
для
гальванического элемента можно рассчитать и некоторые термодинамические
функции, например:
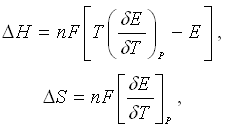
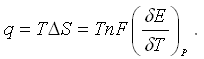
Для измерения разности потенциалов между электродами
гальванического элемента, или электродвижущей силы (ЭДС) элемента, применяют
компенсационный, или уравнительный метод. Наряду с компенсационным методом ЭДС
и потенциалы можно измерять вольтметрами с высокоомным
входом.
Концентрационные элементы состоят из одинаковых электродов,
отличающихся активностями потенциалопределяющего иона. Действительно, из
уравнения Нернста следует, что при a1 > a2
ЭДС концентрационного элемента
равна
ЭДС этих элементов обычно очень мала. Концентрационные
элементы используются при определении pH и
концентраций труднорастворимых солей.
Схема гальванического элемента:
(-) Ag|Ag+ (AgNO3 0.01)||Ag+ (AgNO3
0.1)|Ag (+)
Е = 0,059/1 * lg0.1/0,01 = 0,059 В
Задача 230
Электролиз раствора NaI проводили при силе тока 6 А в
течение 2,5 ч. Составьте электронные уравнения процессов, происходящих на
угольных электродах, и вычислите массу вещества, выделившегося на катоде и
аноде?
Решение:
NaI
↔ Na+ + I-
(-) H+
+ e- = H
2H = H2
(+)I-
- e- = I
2I = I2
Закон Фарадея:
m = MIτ/
(z F)
Т.к.сила тока в 1 А соответствует прохождению 1 к/с, за все
время через растворы прошло 6*2,5*3600 = 54000Кл
Следовательно, выделится
1*54000/1*96487 = 0,55 г
126,9 * 54000/ 1* 96487 = 71,0 г
Список литературы
1. Химия / Под ред. В. Шретера . –
М.: Химия, 1986. – 648 с.
2. Ходаков
Ю.В., Цветков Л.А. Химия – М.: Государственное учебно-педагогическое
издательство министерства просвещения РСФСР, 1961. – 424 с.
3. Рабинович
В.А., Хавин З.Я. Краткий химический справочник. – Л.: Химия, 1977. – 376 с.
4. Краткий
справочник физико-химических величин. – Л.: Химия, 1983. – 232 с.
5. Некрасов Б.В. Учебник общей химии. – М.: Химия, 1972. –
472 с.
[1] Химия / Под ред. В. Шретера . – М.: Химия, 1986. – 648 с.