Вариант Н, К.
|
№ п/п
|
Х, млн. руб.
|
Y, тонн
|
|
1
|
9,5
|
23,9
|
|
2
|
10,3
|
24,7
|
|
3
|
7,9
|
22,4
|
|
4
|
5,6
|
25,1
|
|
5
|
6,1
|
27,0
|
|
6
|
6,8
|
29,4
|
|
7
|
4,2
|
34,2
|
|
8
|
3,5
|
30,6
|
|
9
|
3,2
|
35,2
|
|
10
|
2,0
|
34,0
|
Задача 1. Построить модель связи между указанными факторами, проверить
её адекватность, осуществить точечный и интервальный прогноз.
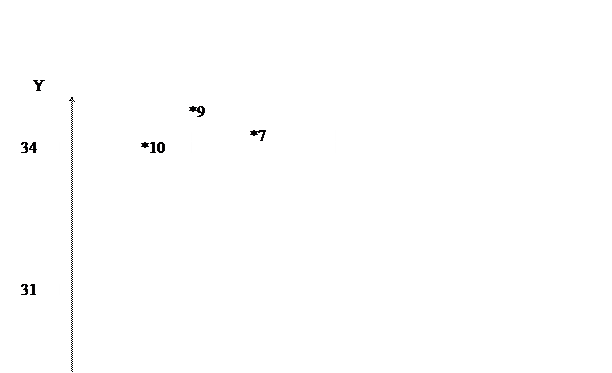
1) Исходные данные
нанесите на координатную плоскость и сделайте предварительное заключение о
наличии связи между Х и Y, а также о её виде (прямая или обратная) и форме (линейная и
нелинейная).
По горизонтальной оси –
стоимость основных производственных фондов – Х, млн. руб;
по вертикальной – среднесуточная производительность – Y,тонн.
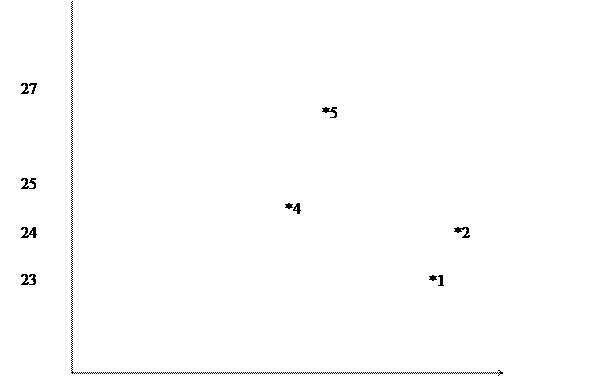
Проанализировав поле
расселения, можно сделать заключение о наличии между факторами Х и Y обратной нелинейной связи.
2) Рассчитайте парный
коэффициент корреляции rxy. Используя t – критерий Стьюдента, проверить
значимость полученного коэффициента корреляции. Сделайте вывод о тесноте связи
между факторами X и Y.
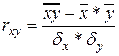
Для нахождения
показателей воспользуемся таблицей.
|
№
|
хi
|
yi
|
xiyi
|
xi2
|
yi2
|
|
1
|
9,5
|
23,9
|
227,05
|
90,25
|
571,21
|
|
2
|
10,3
|
24,7
|
254,41
|
106,09
|
610,09
|
|
3
|
7,9
|
22,4
|
176,96
|
62,41
|
501,76
|
|
4
|
5,6
|
25,1
|
140,56
|
31,36
|
630,01
|
|
5
|
6,1
|
27,0
|
164,7
|
37,21
|
729
|
|
6
|
6,8
|
29,4
|
199,92
|
46,24
|
864,36
|
|
7
|
4,2
|
34,2
|
143,64
|
17,64
|
1169,64
|
|
8
|
3,5
|
30,6
|
107,1
|
12,25
|
936,36
|
|
9
|
3,2
|
35,2
|
112,64
|
10,24
|
1239,04
|
|
10
|
2,0
|
34,0
|
68
|
4
|
1156
|
∑ 59,1 286,5 1534,38 417,69 8407,47
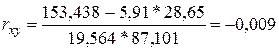
Проверим значимость найденного коэффициента
корреляции, используя критерий Стьюдента.
Гипотеза Н0 –
корреляция между признаками отсутствует;
Н1 – между
признаками существует корреляционная зависимость.
Фактическое значение t – критерия Стьюдента:
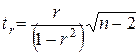
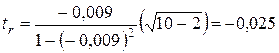
Табличное значение t – критерия:
к = n – 2 = 8
t0,05:8= 2,31
tr ≤ t0,05:8 
принимаем гипотезу Н0.
3) Полагая, что связь
между факторами Х и Y может быть описана линейной функцией, запишите соответствующее уравнение
этой зависимости. Используя процедуру метода наименьших квадратов, получите
систему нормальных уравнений относительно коэффициентов линейного уравнения регрессии.
Любым способом решите её.
Уравнение регрессии имеет
вид:
Система нормальных
уравнений для оценки параметров а и b:
10а + 59,1b = 286,5
59,1а + 417,69b = 1534,38
а = 28,65 – 5,91b
5,91 (28,65 – 5,91b) + 417,69b = 1534,38
а = 28,65 – 5,91b
382,762b = 1365,058
b = 3,566
а = 28,65 – 5,91*3,566
а = 7,575
b = 3,566
Уравнение регрессии.
4) Проверьте значимость
всех параметров модели по t – критерию Стьюдента. Сформулируйте выводы.
Проверим значимость
параметра а:
Н0 – параметр
а не является значимым;
Н1 – параметр
а является значимым.
|
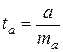
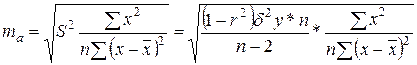
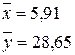
хi
|
yi
|
|
|
|
9,5
|
23,9
|
12,888
|
22,562
|
|
10,3
|
24,7
|
19,272
|
15,602
|
|
7,9
|
22,4
|
3,96
|
39,062
|
|
5,6
|
25,1
|
0,096
|
12,602
|
|
6,1
|
27
|
0,036
|
2,722
|
|
6,8
|
29,4
|
0,792
|
0,562
|
|
4,2
|
34,2
|
2,924
|
30,802
|
|
3,5
|
30,6
|
5,808
|
3,802
|
|
3,2
|
35,2
|
7,344
|
42,902
|
|
2
|
34,0
|
15,288
|
28,622
|
∑ 68,408
199,24
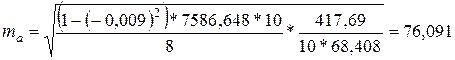
Фактическое значение t – критерия:
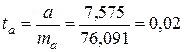
Табличное значение:
t = 2,31
ta ≤ t принимаем гипотезу Н0.
Проверим значимость
параметра b:
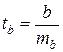
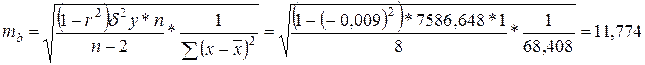
Фактическое значение t
- критерия:
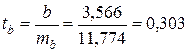
Табличное значение:
t = 2,31
tb ≤ t принимаем
гипотезу Н0.
Таким образом, параметры
уравнения регрессии (а и b) не являются значимыми фактор х не оказывает влияние на
величину y.
5) Проверьте адекватность
модели (уравнение регрессии) в целом с помощью F – критерия. Сформулируйте вывод.
Н0 – фактор х не оказывает влияние на результат у;
Н1 – фактор х оказывает влияние на у.
Рассчитаем фактическое
значение F – критерия:
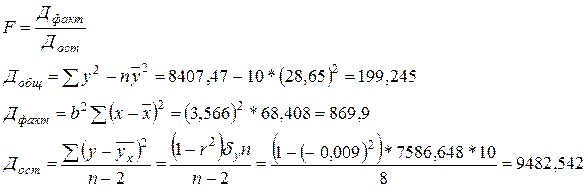
F =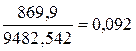 
Табличные значения:
F
=0,05 = 6,61
F=0,01 = 16,26
F ≤ F=0,05
принимаем гипотезу Н0.
F≤ F=0,01
Уравнение регрессии не
является значимым связь между признаками отсутствует.
6) Постройте таблицу
дисперсионного анализа.
Дисперсионный анализ
результатов регрессии:
|
Источники вариации
|
Число
степеней свободы
|
Сумма
квадратов отклонений
|
Дисперсия
на одну степень свободы
|
F - отношение
|
|
Фактическое
|
Табличное
при
 = 0,05
|
|
Общая
Объяснённая
Остаточная
|
9
1
8
|
199,245
869,9
670,655
|
-
869,9
9482,542
|
-
0,092
1
|
-
6,01
-
|
7) Выберем прогнозную
точку:
хn = 11
Рассчитаем у:
у = 7,575 + 3,566х =
7,575 + 3,566*11 = 46,801
8) Рассчитайте доверительные
интервалы для уравнения регрессии и для результативного признака уn при доверительной вероятности = 0,95.
Доверительный интервал
для уравнения регрессии:
b – tmb ≤ b ≤ + tmb
b = 3,566
t = 2,31
mb = 11,744
3,566 – 2,31*11,774 ≤ b ≤ 3,566 + 2,31*11,774
-23,632 ≤ b ≤ 37,896
a - tma ≤ a ≤ a + tma
a = 7,575
t = 2,31
ma =
76,091
7,575 – 2,31*76,091
≤ a ≤ 7,575 + 2,31*76,091
-168,195 ≤ a ≤ 183,345
Доверительный интервал
для уn:
ta = 2,57
= 46,801
myx= S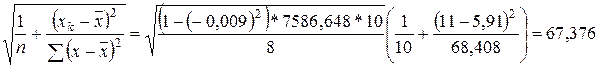
46,804 –
2,57*67,376 ≤ yn
≤ 46,801 +
2,57*67,376
-126,355 ≤ yn ≤ 219,957
9) Изобразите в одной
системе координат исходные данные, линию регрессии, точечный прогноз, 95%
доверительный интервал.
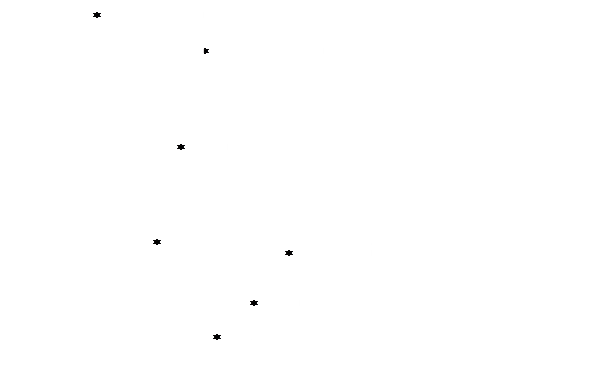
У
