Министерство образования Российской Федерации

ВОРОНЕЖСКИЙ ЗАОЧНЫЙ ФИНАНСОВО ЭКОНОМИЧЕСКИЙ ИНСТИТУТ

КОНТРОЛЬНАЯ РАБОТА

по дисциплине: «Финансовая математика»

	студент           Черных Е.А. курс:             4 факультет:  ФК № зач.           01ФФБ12502
	доцент              Концевая Н.В.

1.    Задание 1.

Дан временной ряд, характеризующий объем кредитования коммерческим банком жилищного строительства (в условных единицах) за 4 года (всего 16 кварталов).

Требуется:

1.      Построить адаптивную мультипликативную модель Хольта-Уинтерса с учетом сезонного фактора, приняв параметры сглаживания a₁ = 0,3; a₂ = 0,6; a₃ = 0,3.

2.      Оценить точность построенной модели с использованием средней относительной ошибки аппроксимации.

3.      Оценить адекватность построенной модели на основе исследования:

-        случайности остаточной компоненты по критерию пико;

-        независимости уровней ряда остатков по d-критерию (критические значения d₁ = 1,10  и d₂ = 1,37) и по первому коэффициенту автокорреляции при критическом значении r₁ = 0,32;

-        нормальности распределения остаточной компоненты по R/S – критерию с критическими значениями от 3 до 4,21.

4.      Построить точечный прогноз на 4 шага вперед, т.е. на 1 год.

5.      Отразить на графике фактические, расчетные и прогнозные данные.

1.1.                    Построение модели Хольта-Уинтерса.

Зависимость между компонентами тренд-сезонного временного ряда мультипликативная. Мультипликативная модель Хольта-Уинтерса с линейным ростом имеет следующий вид:

 

Y_p(t+k)   =   [ a(t) + k · b(t) ] · F(t+k-L)                                (1)

где  k – период упреждения,

    Y_p(t)- расчетное значение экономического показателя для t-го периода;

    a(t) , b(t)  и  F(t) коэффициенты модели, они адаптируются, уточняются   по мере перехода от членов ряда с номером t-1 к t;

   F(t+k-L) – значение коэффициента сезонности того периода, для   которого рассчитывается экономический показатель. L – период сезонности (для квартальных данных L=4, для месячных  L=12). Таким образом, если по формуле 1 рассчитывается значение экономического показателя, например, за второй квартал, то F(t+k-L)  как  раз будет коэффициентом сезонности второго квартала предыдущего года.

Уточнение (адаптация к новому значению параметра  времени t) коэффициентов модели производится с помощью формул:

a(t) =a₁· Y(t) / F(t-L) + (1 - a₁) · [ a(t-1)+b(t-1) ]                      (2)

b(t) =a₃· [ a(t) – a(t-1) ]  +  (1 - a₃) · b(t-1)                                (3)

F(t)=a₂·Y(t) / a(t)+(1-a₂)·F(t-L)                                                 (4)

Параметры сглаживания a₁ , a₂  и  a₃ должны подбираться путем перебора с таким расчетом, чтобы расчетные данные наилучшим образом соответствовали фактическим (то есть чтобы обеспечить удовлетворительную адекватность и точность модели). Для поставленной задачи параметры заданы в условии.

Из формул 1 – 4 видно, что для расчета a(1)  и b(1) необходимо оценить значения этих коэффициентов для предыдущего период времени (то есть для t=1-1=0). Значения a(0)  и b(0)  имеют смысл этих же коэффициентов  для  четвертого квартала года, предшествующего первому году, для которого имеются данные в табл. 1.

Для оценки начальных значений  a(0) и  b(0)  применим линейную модель к первым 8 значениям Y(t)   из табл. 1. Линейная модель,  имеет вид:

Y_p(t)   =   a(0) + b(0)*t                                                                      (5)

Метод наименьших квадратов дает возможность определить коэффициенты линейного уравнения a(0) и  b(0) по формулам (6-9):

  

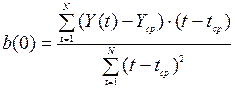          (6)

 

a(0) = Y_cp  - b(0)·t_ср                             (7)

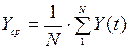                                                        (8)

 

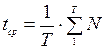                                                                  (9)

Применяя линейную модель к первым 8 значениям  ряда  из таблицы 1 (то есть к данным за  первые 2 года), находим значения  a(0)= 33,893, b(0)= 0,774.

Уравнение (5) с учетом полученных коэффициентов имеет вид: Y_p(t)=33,893+0,774·t. Из этого уравнения находим расчетные  значения Y_p(t) и сопоставляем их с фактическими значениями (см. табл.1). Такое сопоставление позволяет оценить приближенные значения  коэффициентов  сезонности   1 – 4 кварталов F(-3),  F(-2), F(-1)   и F(0) для года, предшествующего первому году, по которому имеются данные в табл. 3.1.  Эти значения  необходимы для расчета коэффициентов сезонности первого года F(1), F(2), F(3), F(4)   и других параметров модели Хольта-Уинтерса по формулам 1-4.

Коэффициент сезонности есть отношение фактического значения экономического показателя к рассчитанному по линейной модели. Поэтому в качестве оценки коэффициента сезонности первого квартала  F(-3) может служить отношение фактических и расчетных значений Y(t) первого квартала первого года, равное Y(1)/Y_p(1)   и такое же отношение для первого квартала второго года (то есть за пятый квартал t=5) Y(5)/Y_p(5). Для  окончательной, более точной оценки этого коэффициента  сезонности можно использовать среднее арифметическое  значение  этих двух величин

F(-3)=[Y(1)/Y_p(1)+Y(5)/Y_p(5)]/2=[30/34,67+32/37,76]/2= =0,86

Аналогично находим  оценки коэффициенты сезонности для второго, третьего и четвертого кварталов:

F(-2) =  [ Y(2)/Y_p(2)  + Y(6)/Y_p(6) ] / 2 =  1,08

F(-1) =  [ Y(3)/Y_p(3)  + Y(7)/Y_p(7) ] / 2 =  1,27

F(0)  =  [ Y(4)/Y_p(4)  + Y(8)/Y_p(8) ] / 2 =  0,79

 

Oценив значения   a(0), b(0), а также F(-3), F(-2), F(-1) и F(0), можно перейти к построению адаптивной мультипликативной модели Хольта-Уинтерса с помощью формул (1-4).

Рассчитаем значения Y_p(t), a(t), b(t) и F(t)  для t=1.

Из уравнение 1, полагая  t=0, k=1  находим  Y_p(1):  

Y_p(0+1)=Y_p(1)=[a(0)+1*b(0)]*F(0+1-4)=[a(0)+1*b(0)]*F(-3)= 29.69

Из уравнение 2-4, полагая  t=1  находим:  

a(1)=a1*Y(1)/F(-3)+(1-a1)*[a(0)+b(0)]=34,78

b(1)=a3*[a(1)–a(0)]+(1-a3)*b(0)=0,81

F(1)=a2*Y(1)/a(1)+(1-a2)*F(-3)=0,86

Продолжая аналогично для t=2,3,4…,16, построим модель Хольта-Уинтерса (табл.3). Максимальное значение t  , для которого можно находить коэффициенты модели,  равно количеству имеющихся данных по экономическому показателю Y(t). В нашем примете данные приведены за 4 года, то есть за 16 кварталов. Максимальное значение t равно 16.

1.2.                    Проверка качества модели.

Будем считать, что условие точности выполнено, если относительная погрешность (абсолютное значение отклонения abs{E(t)} поделенное на фактическое значение Y(t) и выраженное в процентах 100%*abs{E(t)}/Y(t) ) в среднем не превышает 5%.  Суммарное значение относительных погрешностей (см. гр.10 табл.1) составляет 34,90, что дает среднюю величину 34,90/16 = 2,18%.

          Следовательно, условие точности выполнено.

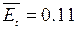
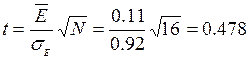
t* _{(a=0.05)N-1=15} = 2,13

Так как |t| < t* условие выполняется, средний уровень Е можно считать нулевым.

1.3.                    Проверка условия адекватности.

Для того, чтобы модель была адекватна исследуемому процессу  ряд остатков E(t) должен обладать свойствами:

а) случайности;

б) независимости последовательных уровней;

в) нормальности распределения.

Проверка случайности уровней. Проверку случайности уровней остаточной компоненты (гр. 9 табл. 1) проводим на основе критерия поворотных точек. Для этого каждый уровень ряда E(t) сравниваем с двумя соседними. Если он больше (либо меньше) обоих соседних уровней, то точка считается поворотной и  в гр. 11 табл. 1 для этой строки ставится 1, иначе в гр. 11  ставится 0. В первой и последней строке гр. 11 табл. 1 ставится прочерк или иной  знак, так как у этого уровня нет двух соседних уровней.

Общее число поворотных точек в нашем примере равно р = 6.

Рассчитаем   значение  q:

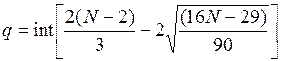
Функция int, означает, что от полученного значения берется только целая часть. При N = 16:

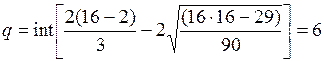
Если количество поворотных точек р больше q, то условие случайности уровней выполнено. В нашем случае р = 6,  q = 6, значит условие случайности уровней ряда остатков невыполнено.

Проверка независимости уровней ряда остатков (отсутствия автокорреляции).

Проверку проводим двумя методами:

а) по d-критерию Дарбина-Уотсона;

б) по первому коэффициенту автокорреляции r₁.

Проверка по d-критерию Дарбина-Уотсона. Для проверки по d-критерию Дарбина-Уотсона рассчитаем значение d:

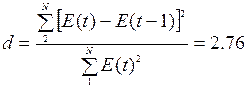                     d = 4-2.76 = 1.24

Примечание. В случае если полученное значение больше 2, значит имеет место отрицательная автокорреляция. В таком случае величину d  уточняют, вычитая полученное значение из 4.

Полученное (или уточненное) значение d  сравнивают с табличными значениями d1и d2. Для нашего случая d1=1.08, а d2=1.36.

Если   0<d<d1, то уровни автокоррелированы, то есть зависимы, модель неадекватна;

Если d1<d<d2, то   критерий    Дарбина –Уотсона  не  дает   ответа на вопрос о независимости уровней ряда остатков. В таком случае необходимо воспользоваться другими критериями (например, проверить независимость уровней     по первому коэффициенту автокорреляции).

Если  d2<d<2 , то уровни ряда остатков являются независимыми.

В нашем случае имеет место отрицательная автокорреляция.

1,08 < 1,24 < 1,36, область неопределенности. Данный критерий не дает ответ на вопрос о независимости уровней ряда остатков.

Проверка по первому коэффициенту автокорреляции r(1).

Рассчитаем r₁  по формуле

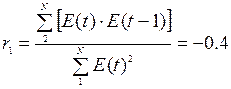
Если модуль рассчитанного значения первого коэффициента автокорреляции меньше критического значения | r₁ |  <  r_таб , то уровни ряда остатков независимы. Для нашей задачи критический уровень r_таб =  0,32. Имеем:

| r₁ | = 0,4  > r_таб  = 0,32       значит уровни зависимы.

Проверка соответствия ряда остатков нормальному распределению определяем по RS – критерию.

Рассчитаем значение RS:

                         RS = ( E_max – E_min ) / S 

где E_max -  максимальное значение уровней ряда остатков E(t)

       E_min - минимальное значение уровней ряда остатков E(t) (см. гр. 9 табл. 1)

S - среднее квадратическое отклонение

E_max = 2,36   E_min = - 1,63 ,   E_max – E_min  = 2,36-(-1,63) = 3,99

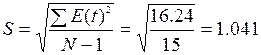
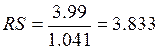
Полученное значение  RS сравнивают с табличными значениями, которые зависят от количества точек N и уровня значимости. Для N=16 и 5% уровня значимости значение RS  для нормального распределения должно находиться в интервале от 3,00 до 4,21

Так как 3,00 < 3,833 < 4,21,     полученное  значение RS попало в заданный интервал. Значит,  уровни ряда остатков подчиняются нормальному распределению.

Таким образом, условия адекватности и точности выполнены не в полном объеме. Следовательно, говорить об удовлетворительном качестве модели нельзя, но так как по заданию необходимо провести прогноз показателя Y_p(t) на 4 квартала вперед, то делать прогноз будем исходя из построенной модели.

1.4.                    Оценка точности.

Т = 100% - D_ср = 100 – 2,18 = 97,82 %, что больше 90%

Т.к. D_ср = 2,18 < 5% - точность высокая.

1.5.                    Расчет прогнозных значений экономического показателя.

Составим  прогноз на  4 квартала вперед (т.е. на 1 год, с t=17 по t=20). Максимальное значение t, для которого могут быть рассчитаны коэффициенты a(t), b(t)  определяется количеством исходных данных и равно 16. Рассчитав значения a(16) и b(16) (см. табл.1), по формуле 1 можно определить прогнозные значения экономического показателя Y_p(t).  Для t=17 имеем:

Y_p(17)=Y_p(16+1)=[a(16)+1·b(16)]*F(16-+1-4)=[a(16)+1·b(16)]·F(13)=

 = [ 48,02 + 1 * 0,92]· 0,89  =  43,46

Аналогично находим Y_p(18), Y_p(19) и  Y_p(20) (см. гр. 8 табл. 1)

 

Таблица 1  Модель Хольта-Уинтерса

t	Фактические значения   yt	Расчетные значения  ŷt= a0 + b0t	yt/ŷt	at	bt	Ft	Модель (ŷ)	Абсол. ошибка Et= yt- ŷt	Относит. ошибка	Поворот-ные точки (Р)	Et2	Et-Et-1	(Et-Et-1)2	Et·Et-1	Et-Eср
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
-3						0,86
-2						1,08
-1						1,27
0				33,89	0,77	0,79
1	30	34,67	0,87	34,78	0,81	0,86	29,69	0,31	1,04%	-	0,10				0,04
2	38	35,44	1,07	35,45	0,77	1,08	38,47	-0,47	1,23%	0	0,22	-0,78	0,61	-0,15	0,33
3	45	36,21	1,24	35,98	0,70	1,26	46,00	-1,00	2,22%	0	1,00	-0,53	0,28	0,47	1,22
4	30	36,99	0,81	37,04	0,80	0,80	29,06	0,94	3,13%	1	0,88	1,94	3,76	-0,94	0,70
5	32	37,76	0,85	37,65	0,75	0,85	32,55	-0,55	1,72%	0	0,30	-1,49	2,22	-0,52	0,43
6	42	38,54	1,09	38,59	0,81	1,08	41,30	0,70	1,68%	1	0,50	1,25	1,57	-0,39	0,36
7	51	39,31	1,30	39,74	0,91	1,27	49,57	1,43	2,80%	0	2,03	0,72	0,52	1,00	1,74
8	31	40,08	0,77	40,03	0,72	0,79	32,63	-1,63	5,27%	1	2,67	-3,06	9,35	-2,33	3,02
9	36			41,18	0,85	0,87	34,81	1,19	3,31%	0	1,42	2,82	7,97	-1,94	1,18
10	46			42,16	0,89	1,09	45,52	0,48	1,04%	0	0,23	-0,71	0,51	0,57	0,14
11	55			43,09	0,90	1,28	54,82	0,18	0,33%	1	0,03	-0,29	0,09	0,09	0,01
12	34			43,78	0,84	0,78	34,57	-0,57	1,67%	0	0,32	-0,75	0,56	-0,10	0,45
13	41			45,43	1,08	0,89	38,64	2,36	5,75%	1	5,55	2,92	8,55	-1,34	5,07
14	50			46,35	1,03	1,08	50,60	-0,60	1,20%	0	0,36	-2,96	8,76	-1,42	0,50
15	60			47,28	1,00	1,27	60,42	-0,42	0,69%	1	0,17	0,19	0,04	0,25	0,27
16	37			48,02	0,92	0,77	37,68	-0,68	1,83%	-	0,46	-0,26	0,07	0,28	0,61
						43,46	1,68	34,90%	6	16,24		44,87	-6,47	16,07
						53,99	0,11	2,18%
							64,59	Max = 2,36
							40,05	Min = -1,63

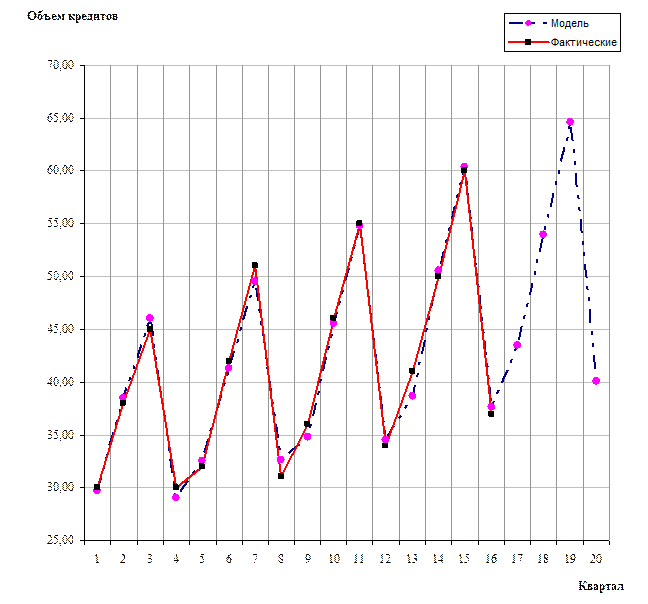
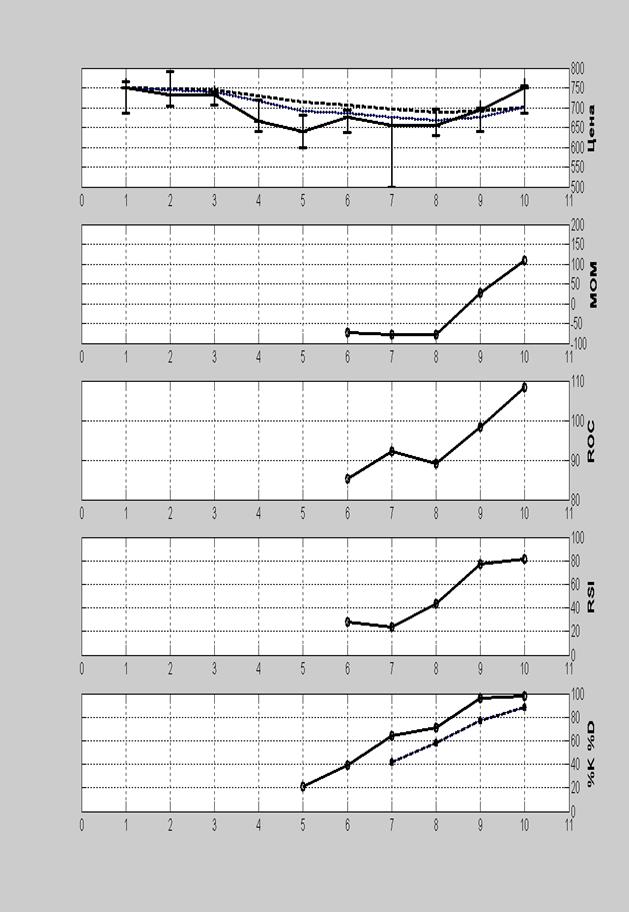
На рис. 1. проводится сопоставление фактических и расчетных данных. Здесь же показаны прогнозные значения цены акции на 1 год вперед. Из рисунка видно, что расчетные данных хорошо согласуются с фактическими, что говорит об удовлетворительном качестве прогноза.

2.    Задание 2.

           

            Даны цены (максимальная, минимальная и закрытия) за 10 дней. Интервал сглаживания принять равным пяти дням. Рассчитать:

-        экспоненциальную скользящую среднюю;

-        момент;

-        скорость изменения цен;

-        индекс относительной силы;

-        %R, %K, %D.

Расчеты проводить для всех дней, для которых эти расчеты можно выполнить на основании имеющихся данных.

Дни	Цены
Макс.	Мин.	Закрытия
1	765	685	750
2	792	703	733
3	740	706	733
4	718	641	666
5	680	600	640
6	693	638	676
7	655	500	654
8	695	630	655
9	700	640	693
10	755	686	750

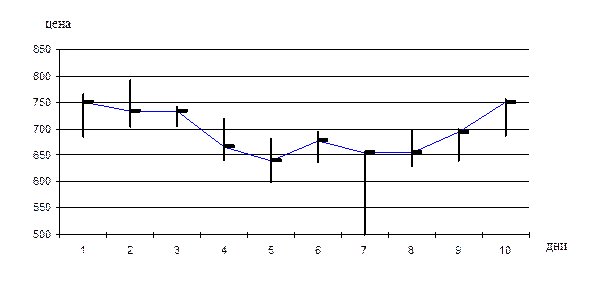
Вывод: Тренд восходящий

2.1.                    Экспоненциальная скользящая средняя (EMA)

При расчете EMA учитываются все цены предшествующего периода. Последним значениям цены придается большое значение, чем предшествующим. Расчеты проводятся по формуле:

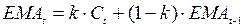
где ;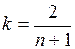

Сt – цена закрытия t-го дня,

EMA_t – значение EMA текущего дня t.

Для  определения момента купли и продажи финансового инструмента руководствуются взаимным расположением двух скользящих средних с различными интервалами сглаживания. Если быстрая скользящая средняя (т.е. с меньшим интервалом сглаживания) пересекает снизу вверх медленную (с большим интервалом сглаживания), целесообразно покупать. При обратной ситуации, когда быстрая скользящая средняя пересекает медленную сверху вниз и идет под ней – надо продавать финансовый инструмент. Этот метод дает хорошие результаты только в условиях явно выраженного восходящего или нисходящего тренда. При отсутствии явно выраженного, устойчивого тренда метод подает ложные сигналы, что приводит к потерям.

При n = 10 EMA1 750,00 EMA2 746,91 EMA3 744,38 EMA4 730,13 EMA5 713,74 EMA6 706,88 EMA7 697,27 EMA8 689,58 EMA9 690,20 EMA10 701,07

При n =5 EMA1 750,00 EMA2 744,33 EMA3 740,56 EMA4 715,70 EMA5 690,47 EMA6 685,65 EMA7 675,10 EMA8 668,40 EMA9 676,60 EMA10 701,07

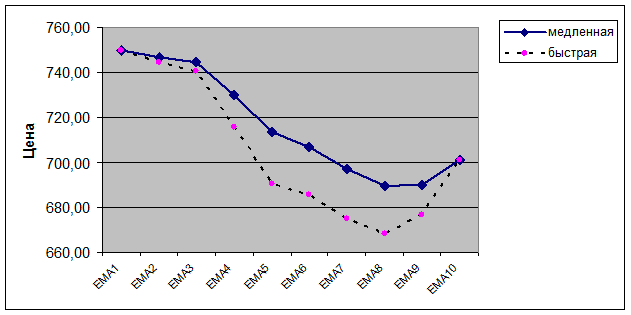
Вывод: исходя из анализа данного показателя сложно сделать вывод покупать или продавать (лучшим вариантом было бы подождать дальнейшего изменения цены, и в зависимости от ее движения делать дальнейшие выводы).

2.2.                    Осцилляторы

Альтернативой скользящим средним, работающим хорошо только в условиях устойчивого тренда, являются осцилляторы. Подаваемые этими индикаторами сигналы наиболее эффективны при бестрендовом рынке (боковом тренде). Кроме того, в период устойчивого тренда они способны предсказывать разворот тренда.

2.2.1.          Момент (momentum – MOM)

Момент рассчитывается как разница конечной цены текущего дня C_t и цены n дней тому назад C_t-n

MOM_t = C_t – C_t-n

где C_t – цена закрытия t-го дня,

МОМ_t – значение МОМ текущего дня.

Положительные значения МОМ свидетельствуют об относительном росте цен, отрицательные – о снижении. Движение графика МОМ вверх из зоны отрицательных в зону положительных значений в точке пересечения нулевой линии дает сигнал к покупке (в случае нисходящего тренда ситуация развивается в обратном направлении).

МОМ6	-74
МОМ7	-79
МОМ8	-78
МОМ9	27
МОМ10	110

Вывод: начальные отрицательные значения свидетельствовали о снижении цен, последующие положительные значения – о росте цен. Движение графика МОМ из области отрицательных значений в область положительных (после восьмого дня) дает сигнал к покупке.

2.2.2.          Скорость изменения цен.

Индикатор рассчитывается как отношение конечной цены текущего дня к цене n дней тому назад, выраженное в процентах.

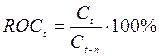
где C_t – цена закрытия t-го дня,

ROC_t – значение ROC  текущего дня.

ROC является отражением скорости изменения цены, а также указывает направление этого изменения. Правила работы ничем не отличаются от МОМ, но вместо нулевой линии для принятия решения о купле или продаже используется уровень 100%. При пересечении этого уровня снизу вверх надо покупать, а при пересечении сверху вниз – продавать финансовый инструмент.

ROC6	85,33%
ROC7	92,22%
ROC8	89,22%
ROC9	98,35%
ROC10	108,28%

Вывод: Показатель ROC дает сигнал на покупку после девятого дня.

2.2.3.          Индекс относительной силы (RSI).

где AU –сумма приростов конечных цен за n последних дней,

      AD – сумма убыли конечных цен за n последних дней.

Значения RSI изменяются от 0 до 100. Этот индикатор может подавать сигналы либо одновременно с разворотом цен, либо с опережением, что является неоценимым достоинством данного индикатора.

Если значение RSI находится в пределах от 80 до 100 (так называемая «зона перекупленности»), значит цены сильно выросли, надо ждать их падения и подготовиться к продаже. Сигналом к продаже служит момент выхода графика RSI из зоны перекуплености.

Если значения RSI находятся в пределах от 0 до 20 (так называемая «зона перепроданности»), значит цены упали слишком низка, надо ждать их роста и подготовиться к покупке. Сигналом к покупке служит момент выхода графика RSI из зоны перепроданности.

Расхождение между направлением движения цен и осциллятора (дивергенция) указывает на близость разворота тренда. Особенно серьезным этот сигнал является, когда осциллятор находится в критической области (перекупленности или перепроданности).

RSI5	0,00
RSI6	27,91
RSI7	23,84
RSI8	43,53
RSI9	77,32
RSI10	81,36

Вывод: Значения RSI после девятого дня перешли в зону  перекуплености. Возможно цены в будущем начнут падать, но готовиться к продаже еще рано, следует подождать момента выхода графика RSI из зоны перекуплености.

2.2.4.          Стахостические линии.

Если МОМ, ROC и RSI используют только цены закрытия, то стахостические линии строятся с использованием более полной информации. При расчете используются также максимальные и минимальные цены. Как правило, применяются следующие стахостические линии: %К, %D, медленная %D и %R.

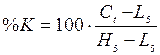
где %К – значения индекса текущего дня,

С₅ – цена закрытия текущего дня t,

L₅ и H₅ – минимальная и максимальная цены за 5 предшествующих дней, включая текущий (в качестве интервала может быть выбрано и другое число дней).

5 день			6 день			7 день
C max	C min		C max	C min		C max	C min
792	600		792	600		740	500
8 день			9 день			10 день
C max	C min		C max	C min		C max	C min
718	500		700	500		755	500

Индекс текущего момента %К

%К5	20,83%
%К6	39,58%
%К7	64,17%
%К8	71,10%
%К9	96,50%
%К10	98,04%

Индекс %D рассчитывается аналогично индексу %К, с той лишь разницей, что при его построении величины (С_t – L₅) и (H₅ – C₅) сглаживают, беря их трехдневную сумму.

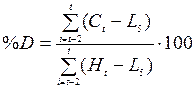
%D7	41,53%
%D8	58,28%
%D9	77,26%
%D10	88,55%

3.    Задание 3.

1.      Банк выдал ссуду, размером 1 000 000 руб. Дата выдачи ссуды – 18.01.02, возврата – 12.03.02. День выдачи и день возврата считать за 1 день. Проценты рассчитываются по простой процентной ставке 15% годовых.

Найти:

a)        точные проценты с точным числом дней ссуды,

b)        обыкновенные проценты с точным числом дней ссуды,

c)        обыкновенные проценты с приближенным числом дней ссуды.

Решение:

I = P·n·i

n = t/K

P – первоначальная сумма денег,

i – ставка простых процентов,

I – наращенные проценты

n – срок ссуды (измеренный в долях года)

К – число дней в году

t – срок операции (ссуды) в днях

t = 13 + 28 + 11 + 1 = 53

a)      К = 365;  t = 53;  I = 1 000 000 · 0,15 · 53 / 365 = 21 780,82 руб.

b)      К = 360;  t = 53;  I = 1 000 000 · 0,15 · 53 / 360 = 22 083,33 руб.

t = 12 + 30 + 12 = 54

c)      К = 360;  t = 54;  I = 1 000 000 · 0,15 · 54 / 360 = 22 500 руб.

2.      Через  180 дней после подписания договора должник уплатит 1 000 000 руб. Кредит выдан под 15% годовых (проценты обыкновенные). Какова первоначальная сумма и дисконт?

Решение:

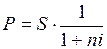
D = S – P

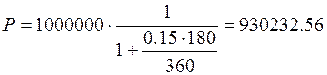руб.

D = 1 000 000 – 930232.56 = 69 767.44 руб.

3.      Через 180 дней предприятие должно получить по векселю 1 000 000 руб. Банк приобрел этот вексель с дисконтом. Банк учел вексель по учетной ставке 15% годовых (год равен 360 дням). Определить полученную предприятием сумму и дисконт.

Решение:

D = S·n·d

P = S – D = S – S·n·d = S(1-n·d)

D = Snd = 1 000 000 · 0.15 · 180 / 360 = 75 000 руб.

P = S – D = 1 000 000 – 75 000 = 925 000 руб.

4.      В кредитном договоре на сумму 1 000 000 руб. и сроком 4 года, зафиксиро-вана ставка сложных процентов, равная 15% годовых. Определить наращенную сумму.

Решение:

S = P (1+i)ⁿ

S = 1 000 000 · (1 + 0.15)⁴ = 1 749 006,25 руб.

5.      Ссуда, размером 1 000 000 руб. предоставлена на 4 года. Проценты сложные, ставка – 15% годовых. Проценты начисляются 2 раза в год. Вычислить наращенную сумму.

Решение:

S = P(1+j/m)^N

Число периодов начисления в году m=2

S = 1 000 000 · (1+0,15 / 2)⁸ = 1 783 477,8 руб.

6.      Вычислить эффективную ставку процента, если банк начисляет проценты 2 раза в году, исходя из номинальной ставки 15% годовых.

Решение:

i_э = (1+j/m)^m – 1

Эффективная ставка показывает, какая годовая ставка сложных процентов дает тот же финансовый результат, что и m-разовое наращение в год по ставке j/m.

i_э = (1+0,15/2)² – 1 = 0,156 т.е. 15,6%

7.      Определить, какой должна быть номинальная ставка при начислении процентов 2 раза в году, чтобы обеспечить эффективную ставку 15% годовых.

Решение:

j = m[( 1+i_э )^1/m – 1]

j = 2·[( 1+0.15)^1/2 – 1] = 0,1448         т.е. 14,48%

8.      Через 4 года предприятию будет выплачена сумма 1 000 000 руб. Определить ее современную стоимость при условии, что применяется сложная процентная ставка 15% годовых.

Решение:

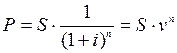
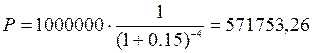 руб.

9.      Через 4 года по векселю должна быть выплачена сумма 1 000 000 руб. Банк учел вексель по сложной учетной ставке 15% годовых. Определить дисконт.

Решение:

P = S(1 - d_сл)ⁿ

где d_сл – сложная годовая учетная ставка

P = 1 000 000 · (1 – 0,15)⁵ = 443 705,3 руб.

D = S – P = 1 000 000 – 443 705,3 = 556 294,7 руб.

10.  В течении 4 лет на расчетный счет в конце каждого года поступает по 1 000000 (1 млн.),  на которые 2 раза в году (m=2) начисляются проценты по сложной годовой ставке 15%. Определить сумму на расчетном счете к концу указанного срока.

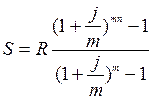
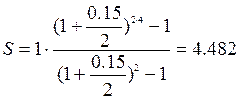  млн.руб.