ВСЕРОССИЙСКИЙ
ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА
СТАТИСТИКИ
О
Т Ч Е Т
о результатах выполнения
компьютерной лабораторной работы №2
Автоматизированный корреляционно-регрессионный анализ взаимосвязи
статистических данных в среде MS Excel
Вариант №99
Выполнила:
ст. III курса гр.345
Акулова Е.Ю.
Ф.И.О.
Проверила:
к.э.н. Калиничева И.Д,
Ф.И.О.
Серпухов, 2007г.
Постановка задачи
Корреляционно-регрессионный анализ взаимосвязи
признаков является составной частью проводимого статистического исследования и
частично использует результаты Лабораторной работы № 1.
В Лабораторной работе № 2 изучается взаимосвязь между
факторным признаком Среднегодовая стоимость
основных производственных фондов (признак Х)
и результативным признаком Выпуск
продукции (признак Y), значениями которых
являются исходные данные Лабораторной работы № 1 после исключения из них
аномальных значений.
Таблица исходных данных
|
Номер предприятия
|
Среднегодовая стоимость основных
производственных фондов, млн.руб.
|
Выпуск продукции, млн. руб.
|
|
1
|
5444,00
|
5201,50
|
|
2
|
6403,50
|
5706,50
|
|
3
|
6605,50
|
6363,00
|
|
4
|
6959,00
|
7070,00
|
|
5
|
4535,00
|
3535,00
|
|
6
|
7312,50
|
6060,00
|
|
7
|
7514,50
|
8181,00
|
|
8
|
5646,00
|
5555,00
|
|
9
|
6908,50
|
6514,50
|
|
10
|
7969,00
|
8130,50
|
|
11
|
8726,50
|
8585,00
|
|
13
|
6656,00
|
6767,00
|
|
14
|
7312,50
|
7373,00
|
|
15
|
8373,00
|
8938,50
|
|
16
|
9585,00
|
9595,00
|
|
17
|
7161,00
|
6464,00
|
|
18
|
7918,50
|
7676,00
|
|
19
|
6302,50
|
4797,50
|
|
20
|
8019,50
|
6565,00
|
|
21
|
8928,50
|
8837,50
|
|
22
|
6151,00
|
4999,50
|
|
23
|
4888,50
|
4696,50
|
|
24
|
8171,00
|
7524,50
|
|
25
|
7312,50
|
6565,00
|
|
26
|
6807,50
|
6211,50
|
|
27
|
5292,50
|
4040,00
|
|
28
|
7110,50
|
6312,50
|
|
29
|
8221,50
|
6918,50
|
|
30
|
7817,50
|
6565,00
|
|
32
|
5747,00
|
5858,00
|
В процессе статистического исследования
необходимо решить ряд задач.
1. Установить наличие статистической
связи между факторным признаком Х
и результативным признаком Y:
а) графическим методом;
б) методом сопоставления параллельных рядов.
2. Установить наличие корреляционной
связи между признаками Х и Y методом аналитической группировки.
3. Оценить тесноту связи признаков Х и
Y на основе:
а) эмпирического корреляционного отношения η;
б) линейного коэффициента корреляции r.
4. Построить однофакторную
линейную регрессионную модель связи признаков Х и Y, используя
инструмент Регрессия надстройки Пакет анализа.
5. Оценить адекватность и
практическую пригодность построенной линейной регрессионной модели, указав:
а) значимость и
доверительные интервалы коэффициентов а0, а1;
б) индекс детерминации R2 и его
значимость;
в) точность регрессионной
модели.
6. Дать экономическую
интерпретацию:
а) коэффициента регрессии а1;
б) коэффициента эластичности КЭ;
в) остаточных величин 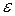 i.
i.
7. Найти наиболее адекватное нелинейное
уравнение регрессии с помощью средств инструмента Мастер диаграмм.
Построить для этого уравнения теоретическую кривую регрессии.
|
Таблица 2,1
|
|
Номер
предприятия
|
Среднегдовая
стоимость основных производственных фондов, млн руб.
|
Выпуск
продукции, млн руб.
|
|
5
|
4535
|
3535
|
|
23
|
4888,5
|
4696,5
|
|
27
|
5292,5
|
4040
|
|
1
|
5444
|
5201,5
|
|
8
|
5646
|
5555
|
|
32
|
5747
|
5858
|
|
22
|
6151
|
4999,5
|
|
19
|
6302,5
|
4797,5
|
|
2
|
6403,5
|
5706,5
|
|
3
|
6605,5
|
6363
|
|
13
|
6656
|
6767
|
|
26
|
6807,5
|
6211,5
|
|
9
|
6908,5
|
6514,5
|
|
4
|
6959
|
7070
|
|
28
|
7110,5
|
6312,5
|
|
17
|
7161
|
6464
|
|
6
|
7312,5
|
6060
|
|
14
|
7312,5
|
7373
|
|
25
|
7312,5
|
6565
|
|
7
|
7514,5
|
8181
|
|
30
|
7817,5
|
6565
|
|
18
|
7918,5
|
7676
|
|
10
|
7969
|
8130,5
|
|
20
|
8019,5
|
6565
|
|
24
|
8171
|
7524,5
|
|
29
|
8221,5
|
6918,5
|
|
15
|
8373
|
8938,5
|
|
11
|
8726,5
|
8585
|
|
21
|
8928,5
|
8837,5
|
|
16
|
9585
|
9595
|
|
Таблица 2,2
|
|
Зависимость выпуска продукции от
среднегодовой стоимости основных фондов
|
|
Номер группы
|
Группы предприятий по стоимости
основных фондов
|
Число предприятий
|
Выпуск продукции
|
|
Всего
|
В среднем на одно предприятие
|
|
1
|
4535
-5545
|
4
|
17473
|
4368,25
|
|
2
|
5545 -
6555
|
5
|
26916,5
|
5383,3
|
|
3
|
6555 -
7565
|
11
|
73881,5
|
6716,5
|
|
4
|
7565 -
8575
|
7
|
52318
|
7474
|
|
5
|
8575
-9585
|
3
|
27017,5
|
9005,8333
|
|
Итого
|
|
30
|
197606,5
|
6586,8833
|
|
Таблица 2,3
|
|
Показатели внутригрупповой
вариации
|
|
Номер группы
|
Группы предприятий по стоимости
основных фондов
|
Число предприятий
|
Внутригрупповая дисперсия
|
|
1
|
4535
-5545
|
4
|
401026,81
|
|
2
|
5545 -
6555
|
5
|
169948,66
|
|
3
|
6555 -
7565
|
11
|
345906,64
|
|
4
|
7565 -
8575
|
7
|
654321,29
|
|
5
|
8575
-9585
|
3
|
184184,72
|
|
Итого
|
|
30
|
1755388,1
|
|
Таблица 2,4
|
|
Показатели дисперсии и эмпирического
корреляционного отношения
|
|
Общая дисперсия
|
Средняя из внутригрупповых
дисперсий
|
Межгрупповая дисперсия
|
Эмпирическое корреляционное
отношение
|
|
2052387,361
|
379720,8906
|
1672666,471
|
0,8149858
|
Таблица 2,5
|
|
|
Линейный коэффициент корреляции
признаков
|
|
|
|
Столбец 1
|
Столбец 2
|
|
|
Столбец
1
|
1
|
|
|
|
Столбец
2
|
0,91318826
|
1
|
|
|
|
|
|
|
|
|
|
ВЫВОД
ИТОГОВ
|
|
|
|
|
Регрессионная статистика
|
|
Множественный
R
|
0,91318826
|
|
R-квадрат
|
0,833912798
|
|
Нормированный
R-квадрат
|
0,827981112
|
|
Стандартная
ошибка
|
604,3372467
|
|
Наблюдения
|
30
|
|
Дисперсионный
анализ
|
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
Регрессия
|
1
|
51345362,62
|
51345363
|
140,58614
|
1,98E-12
|
1
|
|
Остаток
|
28
|
10226258,22
|
365223,51
|
|
|
28
|
|
Итого
|
29
|
61571620,84
|
|
|
|
29
|
|
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
|
Y-пересечение
|
-1103,964244
|
657,9562807
|
-1,6778687
|
0,1045022
|
-2451,73
|
243,7981
|
-1774,32
|
-433,609
|
|
Выпуск
продукции, млн руб.
|
1,089355181
|
0,09187519
|
11,856903
|
1,976E-12
|
0,901157
|
1,277553
|
0,995749
|
1,182962
|
|
ВЫВОД
ОСТАТКА
|
|
|
|
|
|
|
|
Наблюдение
|
Предсказанное Среднегдовая
стоимость основных производственных фондов, млн руб.
|
Остатки
|
|
|
1
|
3836,261501
|
-301,261501
|
|
|
2
|
4221,348558
|
475,1514421
|
|
|
3
|
4661,448051
|
-621,448051
|
|
|
4
|
4826,485361
|
375,0146391
|
|
|
5
|
5046,535107
|
508,4648925
|
|
|
6
|
5156,559981
|
701,4400193
|
|
|
7
|
5596,659474
|
-597,159474
|
|
|
8
|
5761,696784
|
-964,196784
|
|
|
9
|
5871,721657
|
-165,221657
|
|
|
10
|
6091,771404
|
271,2285964
|
|
|
11
|
6146,78384
|
620,2161598
|
|
|
12
|
6311,82115
|
-100,32115
|
|
|
13
|
6421,846023
|
92,65397658
|
|
|
14
|
6476,85846
|
593,1415399
|
|
|
15
|
6641,89577
|
-329,39577
|
|
|
16
|
6696,908207
|
-232,908207
|
|
|
17
|
6861,945517
|
-801,945517
|
|
|
18
|
6861,945517
|
511,0544835
|
|
|
19
|
6861,945517
|
-296,945517
|
|
|
20
|
7081,995263
|
1099,004737
|
|
|
21
|
7412,069883
|
-847,069883
|
|
|
22
|
7522,094756
|
153,9052438
|
|
|
23
|
7577,107193
|
553,3928072
|
|
|
24
|
7632,119629
|
-1067,11963
|
|
|
25
|
7797,156939
|
-272,656939
|
|
|
26
|
7852,169376
|
-933,669376
|
|
|
27
|
8017,206686
|
921,2933141
|
|
|
28
|
8402,293742
|
182,7062576
|
|
|
29
|
8622,343489
|
215,1565111
|
|
|
30
|
9337,505165
|
257,4948348
|
|
|
|
|
|
|
|
II. Выводы по результатам
выполнения лабораторной работы.
Задача 1. Установление наличия статистической связи
между факторным признаком Х и
результативным признаком Y графическим методом и
методом сопоставления параллельных рядов.
Вывод:
Точечный
график связи признаков (диаграмма рассеяния, полученная в Лабораторной работы №1 после удаления аномальных значений),
а также табл.2.1, представляющая два параллельных ряда значений признаков X и Y с ранжированными значениями
xi (В4:С33) показывают, что с увеличением значений факторного признака увеличиваются
значения результативного признака. Это
позволяет сделать вывод, что имеет место статистическая связь. Предположительный
вид связи – линейная прямая.
Задача 2. Установление наличия корреляционной связи между
признаками Х и Y методом аналитической группировки.
Вывод:
Результаты выполнения
аналитической группировки предприятий по факторному признаку Среднегодовая стоимость основных
производственных фондов даны в табл. 2.2 Рабочего файла, которая
показывает, что с увеличением факторного признака Х увеличиваются
средние значения признака Y.
Задача 3.Оценка тесноты связи признаков Х и Y:
а) на основе эмпирического корреляционного отношения.
Для анализа
тесноты связи между факторным и результативным признаками рассчитывается
показатель η - эмпирическое
корреляционное отношение, задаваемое формулой
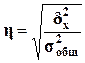 ,
,
где 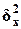 и
и 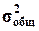 - соответственно
межгрупповая и общая дисперсии результативного признака Y - Выпуск продукции.
- соответственно
межгрупповая и общая дисперсии результативного признака Y - Выпуск продукции.
Результаты
выполненных расчетов представляются табл. 2.4 Рабочего файла.
Вывод:
Значение коэффициента η=0,8149858, что в соответствии с оценочной шкалой Чэддока
говорит о высокой степени связи
изучаемых признаков.
б) на основе линейного
коэффициента корреляции признаков.
В предположении, что связь
между факторным и результативным признаками прямолинейная, для оценки тесноты
связи на основе линейного коэффициента корреляции r был использован инструмент Корреляция
надстройки Пакет анализа, в
результате применения которого построена табл.2.5 Рабочего файла.
Вывод:
Значение
коэффициента корреляции r= 0,91318826 , что в соответствии со шкалой Чэддока
говорит о высокой степени связи
изучаемых признаков.
Так
как значение коэффициента корреляции r положительное ,
то связь между признаками прямая. Посредством показателя η измеряется
теснота связи любой формы, а с помощью коэффициента корреляции r –
только прямолинейная, следовательно, значения η и
r совпадают только при наличии прямолинейной связи. В
теории статистики установлено, что если 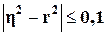 , то гипотезу о прямолинейности связи можно считать
подтвержденной.
, то гипотезу о прямолинейности связи можно считать
подтвержденной.
Вывод:
При
η=0,8149858
и
r= 0,91318826 величина 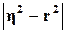 = 0,0982024, следовательно, связь между признаками X и Y
предположительно прямолинейная.
= 0,0982024, следовательно, связь между признаками X и Y
предположительно прямолинейная.
Задача 4. Построение однофакторной линейной регрессионной модели связи
изучаемых признаков с помощью инструмента Регрессия надстройки Пакет
анализа.
Вывод:
Рассчитанные в табл.4.8 (ячейки В91 и В92) коэффициенты а0
и а1
позволяют построить линейную регрессионную модель связи изучаемых признаков в
виде уравнения 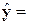 1,089355181х-1103,964244.
1,089355181х-1103,964244.
Задача 5. Оценка адекватности и практической пригодности построенной линейной
регрессионной модели.
1.1. Определение значимости
коэффициентов уравнения.
Уровень
значимости – это величина α=1-Р, где Р заданный уровень
надежности (доверительная вероятность).
Если Р-значение коэффициента
в результативной таблице меньше заданного уровня значимости α=1-0,95=0,05, то этот коэффициент признается неслучайным (типичным для генеральной
совокупности).
Вывод:
Для свободного члена уравнения а0 уровень значимости есть 0,1045022. Так как
этот уровень больше заданного уровня значимости α=0,05, то коэффициент а0= -1103,964244 признается случайным.
Для коэффициента регрессии а1 уровень значимости есть 1,976Е-12 Так как
этот уровень меньше заданного уровня значимости α=0,05, то коэффициент а1=1,089355181 признается типичным.
1.2.
Оценка доверительных интервалов коэффициентов уравнения регрессии.
Доверительные интервалы коэффициентов уравнения
регрессии а0, а1 при уровнях надежности Р=0,95 и Р=0,683 приведены в следующей таблице:
|
Коэффициенты
|
Границы доверительных
интервалов, млн. руб.
|
|
с надежностью Р=0,95
|
с надежностью Р=0,683
|
|
нижняя
|
верхняя
|
нижняя
|
верхняя
|
|
а0
|
-2451,73
|
243,7981
|
-1774,32
|
-433,609
|
|
а1
|
0,901157
|
1,277553
|
0,995749
|
1,182962
|
Вывод:
Увеличение уровня надежности ведет к расширению доверительных
интервалов коэффициентов уравнения, в
которых могут находиться коэффициенты а0, а1
уравнения связи признаков для генеральной совокупности предприятий.
1. Определение практической пригодности
построенной регрессионной модели.
Вывод:
Согласно таблице
"Регрессионная статистика" r=0,91318826, R2=0,833912798. Поскольку 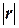 >0,7 и R2>0,5
, то построенная линейная регрессионная модель связи пригодна для практического использования.
>0,7 и R2>0,5
, то построенная линейная регрессионная модель связи пригодна для практического использования.
2. Общая оценка адекватности регрессионной модели по F-критерию Фишера.
Вывод:
Уровень значимости индекса детерминации R2 равен 1,98Е-12. Так
как этот
уровень
меньше заданного
уровня значимости α=0,05, то значение R2 признается типичным и построенная модель связи между признаками Х
и Y применима для генеральной совокупности предприятий
отрасли в целом.
3. Оценка погрешности регрессионной модели.
Погрешность регрессионной модели
можно оценить по средней квадратической ошибке 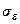 построенного
уравнения регрессии, представляющей собой среднее квадратическое отклонение
эмпирических значений yi признака Y от его теоретических значений
построенного
уравнения регрессии, представляющей собой среднее квадратическое отклонение
эмпирических значений yi признака Y от его теоретических значений 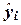 .
.
В адекватных моделях ошибка 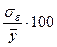 не должна превышать
12%-15%.
не должна превышать
12%-15%.
Вывод:
Погрешность линейной
регрессионной модели составляет 9,17%,
что подтверждает адекватность модели.
Задача 6. Дать экономическую интерпретацию:
1) коэффициента регрессии а1;
2) коэффициента эластичности
КЭ;
3) остаточных величин 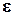 i.
i.
1. Экономическая
интерпретация коэффициента
регрессии а1.
Вывод:
Коэффициент регрессии а1=1,089355181 показывает, что в среднем (в
абсолютном выражении) значения признака Y при
изменении признака Х увеличиваются на 1.089355181.
2.
Экономическая интерпретация коэффициента эластичности.
Вывод:
Коэффициент эластичности КЭ =16,7 показывает, что на 16,7%
изменяется в среднем результативный признак при изменении факторного признака
на 1%.
3.
Экономическая интерпретация остаточных
величин 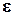 i.
i.
Вывод:
Согласно
таблице остатков, в построенной линейной регрессионной модели наибольшее
превышение среднего объема выпускаемой
продукции 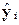 имеют три предприятия
- с номерами 6, 20, 27, а наибольшие
отрицательные отклонения от среднего объема выпуска - три предприятия с
номерами 8, 24, 26. Именно эти шесть предприятий подлежат дальнейшему
экономическому анализу для выяснения причин наибольших отклонений объема
выпускаемого продукта от ожидаемого среднего объема и выявления резервов роста
производства.
имеют три предприятия
- с номерами 6, 20, 27, а наибольшие
отрицательные отклонения от среднего объема выпуска - три предприятия с
номерами 8, 24, 26. Именно эти шесть предприятий подлежат дальнейшему
экономическому анализу для выяснения причин наибольших отклонений объема
выпускаемого продукта от ожидаемого среднего объема и выявления резервов роста
производства.
Задача 7. Нахождение наиболее адекватного нелинейного
уравнения регрессии с помощью средств инструмента Мастер диаграмм. Построение для этого уравнения теоретической
кривой регрессии.
Уравнения регрессии и их графики построены для 4-х
видов нелинейной зависимости между признаками и представлены на диаграмме 2.1
Рабочего файла.
Уравнения регрессии и соответствующие им индексы
детерминации R2 приведены в следующей таблице:
Регрессионные модели связи[1]
|
Вид уравнения
|
Уравнение регрессии
|
Индекс
детерминации R2
|
|
Полином
2-го порядка
|
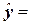 3Е - 0,5 3Е - 0,5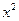 + 0,6701х + 314,35 + 0,6701х + 314,35
|
0,8353
|
|
Полином
3-го порядка
|
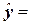 3Е – 0,8 3Е – 0,8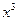 -0,0006 -0,0006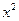 + 5,0568х - 9470 + 5,0568х - 9470
|
0,8381
|
|
Степенное
|
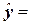 0,1882 0,1882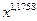
|
0,8371
|
|
Экспоненциальное
|
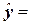 1886,1 1886,1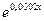
|
0,8272
|
Выбор наиболее адекватного уравнения регрессии
определяется максимальным значением индекса детерминации R2: чем ближе значение R2 к единице, тем более точно
регрессионная модель соответствует фактическим данным.
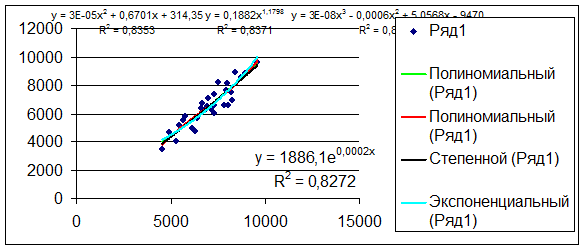
Вывод:
Максимальное значение индекса детерминации R2 = 0,8381, следовательно, наиболее
адекватное нелинейное уравнения регрессии – 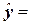 3Е – 0,8
3Е – 0,8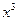 -0,0006
-0,0006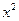 + 5,0568х - 9470
+ 5,0568х - 9470
Это уравнение регрессии и его график приведены на рис.2.2 Рабочего
файла.