5041901(8)

срок 29.04

Требования:  подробные пояснения


Высшая математика

       1.  Вычислить площадь области, заданной неравенствами:

             (x + r)2 + y2 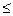 r2,   ,   ,

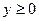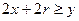             перейдя предварительно к полярным координатам.


2.      Вычислить интеграл (в цилиндрических или сферических координатах)

        ,

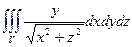      где V – область заданная неравенствами:

      ,    ,    




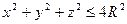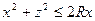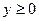
Дискретная математика

Тема «Основные понятия теории множеств».

1.        Пусть  R – множество вещественных чисел,

        , 

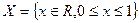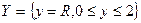
       Что представляют собой множества  XY,   X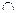Y,   X\Y.


2.        Пусть Х ={-1,-2,-3,1,2,3,0} и Y – множество всех натуральных чисел.

Каждому числу 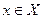  ставиться в соответствие его квадрат.  Выпишите все пары, принадлежащие этому соответствию.

 

3.        Определите свойства следующих отношений:

а) «прямая х пересекает прямую у»  (на множестве прямых);

б) «число х больше числа у на 2» (на множестве натуральных чисел);

в)»число х делится на число у без остатка»  (на множестве натуральных чисел);

г)  «х – сестра у»  (на множестве людей)



Тема: «Основы математической логик», «Основы теории алгоритмов», «Элементы комбинаторного анализа»


1.      Определить, является ли справедливой приведенная формула алгебры высказываний, не  прибегая к составлению таблицы истинности, а используя только свойства соответствующих операций.

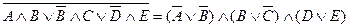
где  A,B,C,D,E – простые высказывания.


  1. Для указанной функции трех переменных:   f(x1,x2, x3) – принимает единичные значения на наборах   № 0,1, 3, 6, 7

-          составить таблицу истинности;

-          определить, к  каким классам булевых функций она относится;

-          записать совершенные ДНФ и КНФ;

-          найти минимальную ДНФ

-          для полученной минимальной ДНФ построить логическую схему в

      базисах: а) 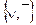 (дизъюнкция, отрицание)

                     б) 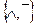  (конъюнкция, отрицание)


  1. Является ли полной система булевых функций, состоящая из импликации и отрицания? Доказать полноту (или неполноту) приведенной системы булевых функций, состоящей       из импликации и отрицания.


  1.  Составить программу машины Тьюринга, уменьшающей данное число на единицу. В результате работы программы происходит следующее преобразование машинных слов:    

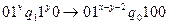
  1. Из колоды, содержащей 52 карты, вынули 10 карт. В скольких случаях окажется, что среди вынутых карт:     а) хотя бы один туз;   б) ровно один туз.