11. Поляризационный метод

локации объекта по дальности с вариацией азимута плоскости

поляризации

   Использование характеристик поляризационного излучения в лазерных системах для селекций полезного сигнала на фоне помех носит весьма ограниченное применение. Использование же явления поляризации для целей дальнометрии ранее никем не рассматривалось. Такой метод из за слабого изменения плоскости поляризации в аэрозольных средах позволяет создать ряд систем дальнометрии на железнодорожном транспорте, инвариантных к аэрозольным помехам[152-158, 162].

11.1.Основные положения

   Поляризационные характеристики сигнала современными методами описываются сферой Пуанкаре, вектором Стокса, вектором Джонса или кванто-механическим представлением. Несмотря на обширные исследования поляризационных характеристик отраженного сигнала, в настоящее время отсутствуют отличительные признаки, обеспечивающие выделение объектов техники на фоне маскирующего рельефа в условиях аэрозольных помех. Основываясь на когерентных свойствах оптических полей, колебание оптического диапазона в любой точке Z пространства в момент времени t можно описать функцией    E(Z,t), которая является действительной функцией времени. При анализе фотоприема случайную функцию V(z,t) связывают с любой компонентой поля Е(z,t) зависимостью вида 

,

где Еi- мнимая компонента, связанная с действительным  преобразованием  Гильберта                           

или                               ,

где ; j(z,y) - фаза узкополосного процесса;w₀ - несущая частота. Мгновенная интенсивность определяется

I(z,t)=V(z,t)V*(z,t),

где V*(z,t) - комплексно-сопряженная величина. Линейная комбинация двух полей находится как

V(z,t)=K₁V(z₁,t-t₁)+K₂V(z₂,t-t₂),

где K₁ и K₂ - коэффициенты пропорциональности; t₁ и t₂ - время прихода волны в заданную точку. Средняя интенсивность в точке суммирования равна

 

B(z₁,z₂,t-t₁) - функция взаимной когерентности:

.

Пусть t₂ - t₁ = t, тогда нормированное значение функции взаимной когерентности),

 ¾

называют коэффициентом когерентности, причем .

Если t = 0, то B(z₁,z₂,0) - пространственная когерентность, если z₁=z₂, то B(z₁,z₂,t) - временная когерентность. Под когерентностью в общем случае понимают временную когерентность на ансамбле 2n точек,  которая определяется как когерентность порядка

.

Если принимаемый сигнал имеет произвольную степень поляризации, то можно использовать метод анализа когерентности, обобщая функции когерентности и поляризации. В этом случае интенсивность определяется на основе матрицы когерентности

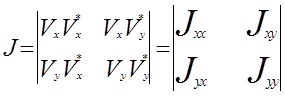,            (11.1)

где V_x=V_x(z,t); V_y=V_y(z,t) - комплексные амплитуды компонент электрического вектора сигнала.

   Диагональные матрицы (1) - действительные числа, определяют интенсивности соответствующих компонент. Недиагональные элементы - комплексны, с их помощью определяют поляризацию принимаемого сигнала. Оценку поляризации удобно производить с помощью коэффициента корреляции

.

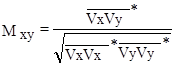Реальный сигнал может иметь произвольную степень поляризации Ј-го можно представить в виде суммы неполяризованной и поляризованной компонент J=J₁+J₂.

Интенсивность поляризованной компоненты определяется через след матрицы J₂

,

где. символ S_р обозначает сумму диагональных элементов матрицы. Степень поляризации при этом равна

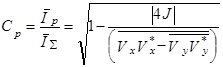
Здесь

 ¾

общая средняя интенсивность. Степень поляризации можно определить через собственные значения `I<sub>1</sub> и `I₂ матриц когерентности J₁ и J₂, то есть

.

На основе показанных аналитические зависимостей можно сделать вывод о том, что поляризационные характеристики зависят от степени поляризации, которая в свою очередь определяется микроструктурой подстилающей поверхности. Однако если учесть, что аэрозольные помехи при однократном рассеянии практически не влияют на обратное рассеяние, и если селектируемый объект (отражатель) железнодорожного транспорта по структуре построения однообразен, целесообразно рассмотреть ряд методов дальнометрии.

   На практике более информативным оказывается вектор поляризации (изменение углового положение анализатора по отношению к поляризатору излучения), на базе которого предлагается ряд методов дальнометрии.  Для измерения дистанции авторами введена терминология как вариация вектора поляризации монохроматического поляризованного света по определенному закону с последующей обработкой отраженного сигнала в анализаторе, плоскость изменения поляризации которого определяется функцией модулирующего сигнала. Если световая волна, входящая в анализатор, линейно поляризована, то для интенсивности волны, выходящей из анализатора, справедлив закон Малюса

,                                   (11.2)

где Р_вх - интенсивность входящего света; К_a - коэффициент прозрачности анализатора; - угол между плоскостями поляризации входящего света, и света, пропускаемого анализатором.

   Таким образом, используя законы модуляции плоскости по­ляризации излучаемого сигнала   за счет сравнения отраженного сигнала с плоскостью поляризации анализатора, можно получить результирующий сигнал с определенным видом модуляции, результирующий спектр и интегральный закон которого, характеризует функцию селекции по дальности.

11.2. Поляризационные методы селекции объекта по дальности с вариацией

 азимута плоскости поляризации

   Пусть плоскость поляризации излучаемого сигнала и анализатора изменяется во времени с частотой _м. Тогда угол между плоскостями поляризации входящего (отраженного) света и света, пропускаемого анализатором, равен

                  (11.3)

где  R - дальность до объекта; с = 3×10⁸м/с. В этом случае амплитуда огибающей на выходе анализатора в пределах фазового цикла определяется фиксируемой дистанцией:

.                                     (11.4)

При выбранной частоте  модуляции плоскости поляризации сигнал на выходе анализатора представляет собой постоянную составляющую, зависящую от времени задержки и отражающих свойств поверхности, что затрудняет выделение цели на фоне помех. Для устранения влияния отражающих свойств поверхности на измерение дистанции можно использовать переключение фазы колебаний плоскости поляризации анализатора на 180⁰ в такт с частотой измерения или применить многоступенчатую модуляцию плоскости поляризации излучаемого сигнала. Устранить неоднозначность и влияние отражающих свойств поверхности возможно также за счет некоторого разноса частоты модуляции плоскости поляризации анализатора, и излучаемого сигнала с измерением периода биения, начиная с момента переключения фазы модуляции плоскости поляризации анализатора. Одним из вариантов устранения постоянной составляющей является введение двух неуправляемых анализаторов: в опорном канале и на пути формирования отраженного сигнала. Тогда результирующий сигнал на входе фотодетектора равен

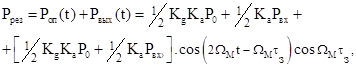 (11.5)

то есть в этом случае переменная составляющая равна удвоен­ной частоте модуляции плоскости поляризации и при нормировке к сомножителю будет промодулирована по дистанции составляющей  , которая несет информацию о дальности.

   Рассмотрим случай, когда частота изменения колебаний плоскости поляризации подчиняется закону

,                              (11.6)

где  - диапазон частоты изменения плоскости поляризации. Тогда функция изменения фазы колебаний плоскости поляризации равна

.                           (11.7)

Учитывая, что  результирующий сигнал найдем как

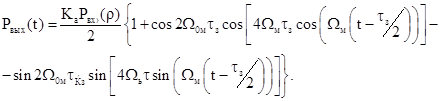(11.8)

Фазовое соотношение  представим в виде:

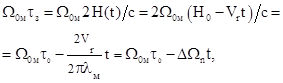            (11.9)

где  - длина волны модуляции плоскости поляризации сигнала, соответственно

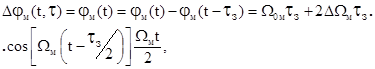(11.10).

 - изменение приращения плоскости поляризации за счет относительного сближения измерительной системы с преградой (эффект, ранее нигде не описанный). Разлагая в ряд по функциям Бесселя составляющие

и

после соответствующих преобразований с точностью да постоянных фазовых соотношений получим следующее выражение для сигнала на выходе фотоприемника

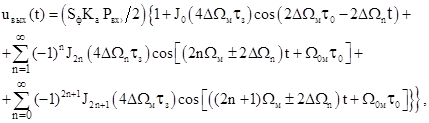
(11.11)

где  - функция Бесселя первого рода n-го порядка от аргумента . Впервые показано наличие приращения частоты изменения плоскости поляризации в отраженном сигнале , в процессе сближения описанной лазерной системы с объектом. Здесь спектр сигнала на выходе фотодетектора близок к спектру сигнала с частотной модуляцией. То есть характер изменения амплитуды каждой гармонической составляющей сигнала по дистанциям определяется поведением соответствующих функций Бесселя. При этом возможны различные варианты построения лазерных датчиков, использующих модуляцию плоскости поляризации, как, например: с фиксацией дистанции по равно-сигналъной зоне; регистрацией дистанции с использованием нелинейного элемента, с выделением удвоенного приращения плоскости поляризации  или удвоенной гармоники принимаемого сигнала и т.д.

   Реализация данного метода в системах ближней дальнометрии связана с выработкой условий адаптации лазерной системы к сигналу аэрозольной помехи. Сравнивая данные по структуре сигнала по поляризационным признакам с поляризационными признаками помехового сигнала, приходим к выводу, что для лазерного датчика с однократным рассеянием помехового сигнала можно выделить следующие отличительные особенности:

· азимут плоскости поляризации для сигнала, отраженного от аэрозольной помехи, близок к нулю (коэффициент поляризации );

· азимут плоскости поляризации отраженного сигнала от цели и цели, прикрытой помехой, всегда для всех возможных условий встреч намного больше одного градуса.

   Практическая реализация процесса адаптации сводится к изменению плоскости поляризации анализатора с определенным тактом поворота  и вычислению азимутального угла 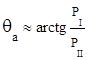 c последующим изменением порога приема. В частном случае при  порог срабатывания устанавливается максимальным, то есть происходит блокировка канала. Вероятность пропуска процесса регистрации объекта определяется условием ослабления сигнала в аэрозольной среде, с учетом дистанции между лазерной системой и объектом.

11.3. Экспериментальное моделирование

   По данным измерения сигнала на выходе, в зависимости от положения анализатора регистрировались интенсивности амплитуд сигналов для двух взаимно перпендикулярных плоскостей электрического вектора, одно из которых совпадало с плоскостью поляризации излученного сигнала (I₂=I₄). Расчетным путем определялись азимут плоскости поляризации отраженного сигнала q_p, модуль  и коэффициент поляризации С_р. Следует отметить, что при взаимодействии поляризованного излучения с поверхностно-протяженными объектами положение вектора поляризации сильно изменяется в зависимости от соотношения между длиной волны и высотой шероховатости поверхности, то есть от соотношения между диффузной и зеркальной составляющими. Для листвы и многих видов земного покрова среднее значение и дисперсия азимута плоскости поляризации имеют гораздо большее значение, а коэффициент поляризации  меньшее, чем железнодорожного состава.

   Следует отметить, что для водной поверхности при отсутствии фазовых сдвигов между ортогональными поляризационными компонентами отраженный сигнал практически не меняет положения вектора поляризации. Обобщенные данные экспериментальных исследований представлены в таблицах 11.1 и 11.2.

   В табл. 11.1. приведено изменение угловых характеристик положения вектора поляризации (M(qр)-математическое ожидание; D(qр)-дисперсия; 

 -

коэффициент вариации)и среднего значения коэффициента поляризации  в зависимости от вида поверхности и угла облучения a_об

   В табл.11.2. приведено изменение угловых характеристик положения вектора поляризации: (M(qр) - математическое ожидание; D(qр) - дисперсия;

 - коэффициент вариации и среднего значения коэффициента поляризации  в зависимости от вида поверхности и угла облучения a_об

 

Угол облу	aоб=90°	aоб=75°	aоб=60°
Повер хности	M(qр)	D(qр)	var	``СР	M(qр)	D(qр)	var	``СР	M(qр)	D(qр)	var	``Cp
Блок покрытый краско	6,1	1,26	5,40	0,80	22,7	3,94	11,5	0,45	28,2	4,0	14,1	0,34
Деревянный каркас	15,8	2,83	9,40	0,46	17,2	8,40	5,90	0,52	17,4	1,1	16,3	0,52
Асфальт сухой	24,9	66,8	3,10	0,33	26,9	22,9	5,60	0,30	29,3	4,6	13,9	0,27
Асфальт мокрый	8,2	77,4	0,90	0,87	25,0	83,9	2,70	0,44	30,0	34,2	5,10	0,22
Снег	43,2	0,60	139,4	0,04	42,9	1,50	34,6	0,07	42,5	11,2	12,7	0,02
Песок	35,3	10,7	10,8	0,16	34,7	7,70	12,5	0,18	36,3	5,5	15,8	0,16
Зеленая листва	23,5	58,3	3,06	0,40	27,2	40,4	4,28	0,36	28,1	48,2	4,04	0,33
Палая листва	31,0	6,0	12,6	0,16	31,1	23,6	6,40	0,21	33,9	19,8	7,60	0,21
Тес	31,1	15,4	7,90	0,20	36,3	4,40	17,3	0,14	38,2	4,0	19,1	0,11
Чернозем сухой	24,2	9,8	7,70	0,38	23,1	7,00	8,40	0,40	24,3	12,9	6,40	0,37
Дерн	25,8	9,8	8,30	0,35	25,8	23,4	5,30	0,36	28,4	9,6	9,2	0,35
Грязь	12,9	40,7	2,00	0,70	11,3	13,6	3,90	0,70	16,8	17,9	3,60	0,55

Таблица 11.1.

Угол облучения	aоб=90°	aоб=75°	aоб=60°
Поверхности	M(qр) (qр)	D(qр)	var	``СР	M(qр)	D(qр)	var	``СР	м(qр)	D(qр)	var	`Ср`
Блок покрытый серой защитной краской	6,1	1,26	5,40	0,80	22,7	3,94	11,5	0,45	28,2	4,0	14,1	0,34
Деревянный каркас, покрытый зелено защитной краской	15,8	2,83	9,40	0,46	17,2	8,40	5,90	0,52	17,4	1,1	16,3	0,52
Асфальт сухой	24,9	66,8	3,10	0,33	26,9	22,9	5,60	0,30	29,3	4,6	13,9	0,27
Асфальт мокрый	8,2	77,4	0,90	0,87	25,0	83,9	2,70	0,44	30,0	34,2	5,10	0,22
Снег	43,2	0,60	139,4	0,04	42,9	1,50	34,6	0,07	42,5	11,2	12,7	0,02
Песок	35,3	10,7	10,8	0,16	34,7	7,70	12,5	0,18	36,3	5,5	15,8	0,16
Зеленая листва	23,5	58,3	3,06	0,40	27,2	40,4	4,28	0,36	28,1	48,2	4,04	0,33
Палая листва	31,0	6,0	12,6	0,16	31,1	23,6	6,40	0,21	33,9	19,8	7,60	0,21
Тес	31,1	15,4	7,90	0,20	36,3	4,40	17,3	0,14	38,2	4,0	19,1	0,11
Чернозем сухой	24,2	9,8	7,70	0,38	23,1	7,00	8,40	0,40	24,3	12,9	6,40	0,37
Дерн	25,8	9,8	8,30	0,35	25,8	23,4	5,30	0,36	28,4	9,6	9,2	0,35
Грязь	12,9	40,7	2,00	0,70	11,3	13,6	3,90	0,70	16,8	17,9	3,60	0,55

Таблица 11.2.

   Следует отметить, что при взаимодействии поляризованного излучения с поверхностно-протяженными объектами положение вектора поляризации сильно изменяется в зависимости от соотношения между длиной волны и высотой шероховатости поверхности, то есть от соотношения между диффузной и зеркальной составляющими. Для листвы и многих видов земного покрова среднее значение и дисперсия азимута плоскости поляризации имеют гораздо большее значение, а коэффициент поляризации  меньшее, чем железнодорожного транспорта. Установлено, что для водной поверхности при отсутствии фазовых сдвигов между ортогональными поляризационными компонентами отраженный сигнал практически не меняет положения вектора поляризации.

   На основе представленных данных можно сделать вывод о том, что статистические поляризационные отраженного сигнала существенно изменяются от вида материала отражателя, т.е определяются микроструктурой подстилающей поверхности, а при определенном конструктивном решении  вектор поляризации не меняет своего значения в широком диапазоне плотностей аэрозольных помех, т.е. при наличии однократного обратного рассеяния. Поэтому предлагаемые методы селекции для определенного вида отражателя, установленного на железнодорожной платформе, обеспечивают надежную селекцию транспорта при действии указанных дестабилизирующих факторов.