10. Фазоимпульсные лазерные
системы селекции объектов
Решение проблемы повышения точности в
импульсных системах за счет сокращения длительности без соблюдения условий
преобразования энергетического подобия приводит к значительным потерям. В связи
с этим весьма перспективными представляются фазоимпульсные методы, в которых
импульсный характер излучения сочетался бы с высокоточным фазовым методом
дальнометрии. Фазоимпульсные методы обработки сигнала можно подразделить на варианты:
· с
оценкой дистанции по фазовым отношениям в контуре ударного возбуждения;
·
фиксацией запаздывания отраженного импульса через измерение величины фазы
опорного сигнала;
·
преобразованием частоты гармонических составляющих огибающих отраженного и
излученного сигналов;
·
модуляцией излученного импульса колебаниями с определенным законом.
Несмотря на очевидные преимущества,
разнообразие вариантов этого метода дальнометрии и большой объем исследований,
проведенный в этом направлении, последний имеет весьма ограниченное применение
в опытно-конструкторских разработках, так как процесс обработки сигнала
наиболее предпочтителен при использовании фотоприемников, с управляемым
(модулирующим) электродом.
Существующие фотоэлектронные умножители не отвечают требованиям
долговечности работы, радиационной стойкости и т.д., а канальные ФЭУ не
подходят для малогабаритных датчиков. Разработанные в последнее время канальные
фотоприемники на МДП-структурах
позволяют надеяться на широкое использование этих методов в системах лазерной
ближней локации. По помехозащищенности фазоимпульсные методы приближаются к
импульсным или фазовым системам. С этой точки зрения наиболее предпочтительным
является метод с модуляцией излученного импульса высокочастотными колебаниями,
в котором неоднозначность устраняется за счет импульсного излучения, а
необходимая помехозащищенность достигается за счет создания знакопеременной
функции селекции
посредством высокочастотного модулирующего сигнала. Опыт отработки такой
системы показал, что даже, при простейшей технической реализации этого метода,
когда излученный сигнал может быть представлен в виде пакета импульсов, а прием
осуществляется в 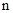 - кратно стробируемом
фотоприемнике, внедрение этого метода ограничено сложностью построения и
габаритно-весовыми характеристиками генератора накачки ПКГ. Из проведенных исследований
в этом направлении следует, что весьма перспективным ключом здесь является
применение лавинно-пролетных диодов. При генерации в таких диодах частот <
100 МГц имеется возможность устранить существующие технические ограничения. Не останавливаясь на многочисленных теоретических и
экспериментальных исследованиях[159-161, 163-167], рассмотрим из приведенной классификации лишь
первые методы, в которых частично снимаются ограничения по применению
определенного класса фотоприемников.
- кратно стробируемом
фотоприемнике, внедрение этого метода ограничено сложностью построения и
габаритно-весовыми характеристиками генератора накачки ПКГ. Из проведенных исследований
в этом направлении следует, что весьма перспективным ключом здесь является
применение лавинно-пролетных диодов. При генерации в таких диодах частот <
100 МГц имеется возможность устранить существующие технические ограничения. Не останавливаясь на многочисленных теоретических и
экспериментальных исследованиях[159-161, 163-167], рассмотрим из приведенной классификации лишь
первые методы, в которых частично снимаются ограничения по применению
определенного класса фотоприемников.
10.1.
Фазоимпульсный лазерный датчик с оценкой временного положения импульса по
фазовым соотношениям в контурах ударного возбуждения
При относительно высокой частоте опорного
гармонического колебания возникает ошибка, связанная с привязкой низкой частоты
излучения и определенному фазовому набегу опорного сигнала. Особенно острой эта
проблема становится при использовании в генераторах накачки ключевых элементов,
обладающих значительным разбросом задержки между управляющим сигналом и лавинообразным
процессом формирования токового импульса. Формирование функции селекции по
дальности возможно по нескольким направлениям: опорный сигнал представляет
собой отрезок затухающего колебания, формируемый контуром ударного возбуждения,
а принятый сигнал сравнивается с опорным. Для формирования необходимой
"мертвой зоны" затухающее колебание задерживается на величину 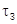 относительно
излученного. Функция селекции по дальности повторяет форму опорного колебания.
При отсутствии переходного процесса на выходе фотоприемника при действии
опорного сигнала количество колебаний в последнем можно ограничить двумя
периодами, что позволяет устранить неоднозначность и повысить точность отсчета
высоты срабатывания Ноп. Влияние изменения амплитуды на точность
фиксации в данном случае устраняется стабилизацией амплитуды входного сигнала и
изменением фазы опорного сигнала на
относительно
излученного. Функция селекции по дальности повторяет форму опорного колебания.
При отсутствии переходного процесса на выходе фотоприемника при действии
опорного сигнала количество колебаний в последнем можно ограничить двумя
периодами, что позволяет устранить неоднозначность и повысить точность отсчета
высоты срабатывания Ноп. Влияние изменения амплитуды на точность
фиксации в данном случае устраняется стабилизацией амплитуды входного сигнала и
изменением фазы опорного сигнала на 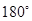 в такт с
посылкой зондирующих импульсов. Энергетические затраты при этом определяются
выбором рациональных параметров фотоприемного тракта
с реактивной нагрузкой. Коротко
остановимся на этом вопросе.
в такт с
посылкой зондирующих импульсов. Энергетические затраты при этом определяются
выбором рациональных параметров фотоприемного тракта
с реактивной нагрузкой. Коротко
остановимся на этом вопросе.
Согласно эквивалентной схеме
(рис.10.1.) передаточная характеристика
нагрузки фотодиода равна
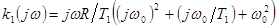 , (10.1)
, (10.1)
где 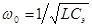 ;
; 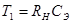 ;
; 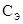 - квивалентная емкость;
- квивалентная емкость; 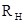 - активное сопротивление
нагрузки. С помощью теории вычетов найдем импульсную характеристику
фотоприемника, которая при условии
- активное сопротивление
нагрузки. С помощью теории вычетов найдем импульсную характеристику
фотоприемника, которая при условии 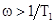 имеет колебательный
характер
имеет колебательный
характер
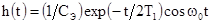 ,
,
где 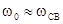 ;
; 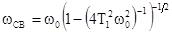 .
.
Пусть на вход фотоприемника, воздействует
световой импуль
Рис. 10.1. Эквивалентная схема фотоприемного
тракта:
а) фотодиода с инерционным звеном; б) избирательного
усилителя
с прямоугольной
формой огибающей 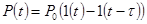 , где
, где 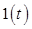 -
единичная функция перепада. Тогда результирующий сигнал на нагрузке фотодиода
описывается выражением
-
единичная функция перепада. Тогда результирующий сигнал на нагрузке фотодиода
описывается выражением
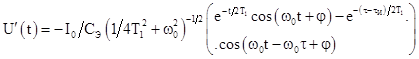 ,
,
где 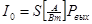 ,
, 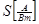 -
крутизна вольт-амперной
характеристики фотодиода. В реальных системах используются достаточно короткие
оптические сигналы, для которых справедливо неравенство
-
крутизна вольт-амперной
характеристики фотодиода. В реальных системах используются достаточно короткие
оптические сигналы, для которых справедливо неравенство 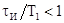 , то есть
, то есть 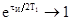 , и можно записать
, и можно записать
Амплитуда
входного сигнала равна
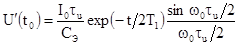
Ее значение при сверхкоротких
световых импульсах 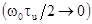
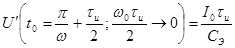
совпадает с амплитудой сигнала
на выходе альтернативного варианта токоприемника с чисто активной нагрузкой 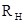 при условии
при условии 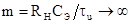 , то есть при значительном отклонении параметров
фотоприемника от квазиоптимальных пиковое значение выходных
колебаний одинаково для данных видов нагрузки фотодетектора. Этот вывод,
справедливый также для оптических импульсов другой формы.
, то есть при значительном отклонении параметров
фотоприемника от квазиоптимальных пиковое значение выходных
колебаний одинаково для данных видов нагрузки фотодетектора. Этот вывод,
справедливый также для оптических импульсов другой формы.
Квазиоптимальные
параметры реактивной нагрузки детектора найдем, максимизируя
отношение сигнал/шум. Корреляционная функция шумового процесса на выходе фотодиода
при воздействии на вход дробового шума с энергетической плотностью 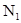 , имеет вид
, имеет вид
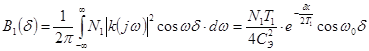 .
.
Соответственно дисперсия напряжения этого шума
равна
где 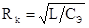 - характеристическое
сопротивление. Отношение сигнал/шум на выходе фотоприемника описывается выражением
- характеристическое
сопротивление. Отношение сигнал/шум на выходе фотоприемника описывается выражением
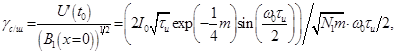
(10.3)
где 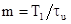 ;
; 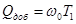 - добротность колебательного контура.
Приближение
- добротность колебательного контура.
Приближение 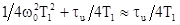 , выполняется обычно с погрешностью 5% при
, выполняется обычно с погрешностью 5% при 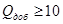 . Кроме того, более, широкополосные фотоприемники с
реактивной нагрузкой сложно реализовать в малом объеме. Учитывая, что данный
случай малой добротности близок к известным решениям для фотоприемников, с
активной нагрузкой, ограничимся анализом выражения при условии
. Кроме того, более, широкополосные фотоприемники с
реактивной нагрузкой сложно реализовать в малом объеме. Учитывая, что данный
случай малой добротности близок к известным решениям для фотоприемников, с
активной нагрузкой, ограничимся анализом выражения при условии 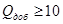 . При уменьшении резонансной частоты (если полоса пропускания
остается неизменной, а условие
. При уменьшении резонансной частоты (если полоса пропускания
остается неизменной, а условие 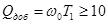 выполняется)
чувствительность фотодетектора улучшается по закону
выполняется)
чувствительность фотодетектора улучшается по закону 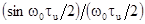 , что подтверждается эксперимент. Если
добротность колебательного контура поддерживается постоянной, то с уменьшением
резонансной частоты во столько же раз сужается
полоса пропускания фотоприемника. При этом это выражение принимает следующий
вид:
, что подтверждается эксперимент. Если
добротность колебательного контура поддерживается постоянной, то с уменьшением
резонансной частоты во столько же раз сужается
полоса пропускания фотоприемника. При этом это выражение принимает следующий
вид:
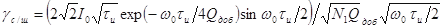 . (10.4)
. (10.4)
В данном случае имеется квазиоптимальное
значение резонансной частоты 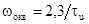 , которое получается из
уравнения путем решения трансцедентного уравнения
, которое получается из
уравнения путем решения трансцедентного уравнения
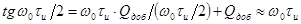 .
.
С учетом этого чувствительность квазиоптимального фотоприемника определяется формулой
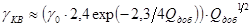 ,
,
где 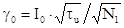 -
отношение сигнал/шум на выходе оптимального фильтра. При
-
отношение сигнал/шум на выходе оптимального фильтра. При 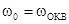 и
и 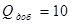 фотоприемник с реактивной
нагрузкой уступает в чувствительности оптимальному фильтру лишь на 28%.
фотоприемник с реактивной
нагрузкой уступает в чувствительности оптимальному фильтру лишь на 28%.
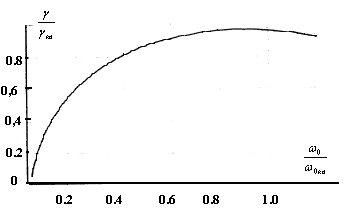
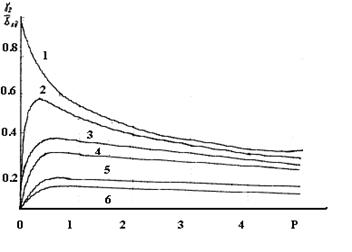
Характерно, что существенное
уменьшение резонансной частоты с одновременным сужением полосы пропускания
фотоприемника приводит к незначительному ухудшению чувствительности
(рис.10.2), например,
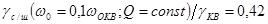 .
.
|
Рис.10.2.
Изменение чувствительности фотоприёмника от резонансной частоты контура при
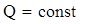 , где , где 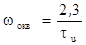 . .
|
|
Для
выбора параметров усилительного тракта эквивалентная схема которого изображена
на рис. 10.1 б, рассмотрим форму сигнала
на его выходе упрощенным методом с использованием "укороченной"
импульсной характеристики. Так как импульсная характеристика избирательного
усилителя имеет вид
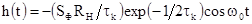 ,
,
то
огибающая этой импульсной характеристики равная 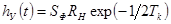 , где
, где 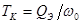 -
постоянная времени усилителя. Согласно приведенным соотношениям огибающая колебаний
на выходе усилителя описывается выражением
-
постоянная времени усилителя. Согласно приведенным соотношениям огибающая колебаний
на выходе усилителя описывается выражением
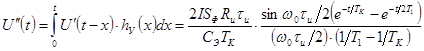 .
.
В
момент времени 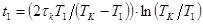 функция
функция 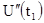 имеет наибольшее значение
имеет наибольшее значение
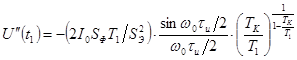 .
.
Характерное для АЧХ усилителя выражение имеет вид:
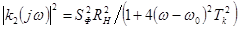 ,
,
поэтому
корреляционная функция теплового шума усилителя, имеющего плотность 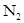 на его выходе, равна.
на его выходе, равна.
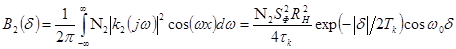
Корреляционная
функция дробовых шумов на выходе фотоприемного тракта
находится с помощью теории вычетов.
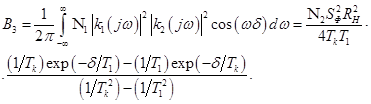
Среднее
квадратичное отклонение суммарного шума на выходе усилителя определяется как
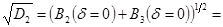
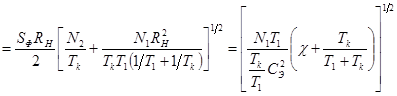 ,
,
где 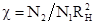 . Отношение сигнал/шум на выходе фото приемного устройства
описывается формулой
. Отношение сигнал/шум на выходе фото приемного устройства
описывается формулой
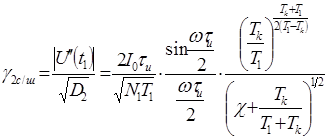
и
зависит как от соотношения уровней теплового и дробового шумов, так и от
инерционности усилителя. Степень ухудшения чувствительности фотоприемного
тракта при наличии реального инерционного шумящего усилителя оценивается
выражением
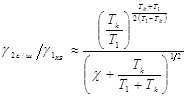 .
.
Отсутствие в полученной формуле
параметров 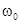 и
и 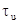 свидетельствует о том,
что отношения сигнал/шум на выходе фотоприемного
устройства и инерционного фотодетектора одинаково зависят от длительности
прямоугольных импульсов и резонансной частоты реактивной нагрузки. Из графиков функций
свидетельствует о том,
что отношения сигнал/шум на выходе фотоприемного
устройства и инерционного фотодетектора одинаково зависят от длительности
прямоугольных импульсов и резонансной частоты реактивной нагрузки. Из графиков функций 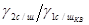 следует, что при
использовании шумящего усилителя существует квазиопимальное
значение его полосы пропускания (масштабный коэффициент
следует, что при
использовании шумящего усилителя существует квазиопимальное
значение его полосы пропускания (масштабный коэффициент 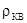 ), максимизирующее отношение
сигнал/шум на выходе тракта. С увеличением уровня шумов усилителя
чувствительность фотоприемного устройства ухудшается,
а величина
), максимизирующее отношение
сигнал/шум на выходе тракта. С увеличением уровня шумов усилителя
чувствительность фотоприемного устройства ухудшается,
а величина 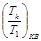 стремится к единице
(график зависимости
стремится к единице
(график зависимости 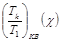 полученной с помощью
ЭВМ, представлен на рис.10.4 ).
полученной с помощью
ЭВМ, представлен на рис.10.4 ).
Поскольку в большинстве случаев плотность
мощности шума ФД значительно меньше плотности мощности шума усилителя (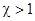 ), можно сделать вывод о возможности существенного сужения полосы
пропускания и использования преобразования импульсного сигнала, в гармоническое
в фазоимпульсных методах дальнометрии. Введение
контура ударного возбуждения в качестве нагрузки фотодетектора в фазоимпульсных
лазерных системах позволяет вести обработку сигнала в относительно узкополосном
тракте. Однако при этом имеют место потери, определяемые для прямоугольного
светового импульса
), можно сделать вывод о возможности существенного сужения полосы
пропускания и использования преобразования импульсного сигнала, в гармоническое
в фазоимпульсных методах дальнометрии. Введение
контура ударного возбуждения в качестве нагрузки фотодетектора в фазоимпульсных
лазерных системах позволяет вести обработку сигнала в относительно узкополосном
тракте. Однако при этом имеют место потери, определяемые для прямоугольного
светового импульса
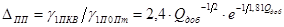 ,
,
где 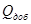 -
добротность контура.
-
добротность контура.

|
|
|
Рис.10.4. Изменение квазиоптимальной
полосы пропускания усилителя, определяемого масштабным коэффициентом 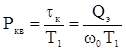 в зависимости от
отношения тепловых шумов усилителя к дробовым в зависимости от
отношения тепловых шумов усилителя к дробовым 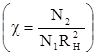
|
|
Для рассматриваемых случаев с
увеличением добротности потери растут, но при этом увеличивается и число колебаний в переходном
процессе. Использование
внутренней структуры такого
колебательного процесса
позволяет скомпенсировать указанные
потери.
Рассмотрим случай, когда в качестве
признака сигнала наряду с фазовыми соотношениями используется и энергия колебательного
процесса. Остановимся
на решении, при котором в качестве накопителя энергии используется оптимальный фильтр. Для прямоугольной световой вспышки
сигнал на выходе контура
ударного возбуждения
представим в виде ранее определенной зависимости,
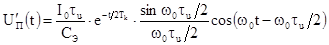 ,
,
а корреляционную функцию шумового процесса выразим как
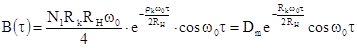 ,
,
где 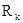 - характеристическое сопротивление контура.
Спектр сигнала
- характеристическое сопротивление контура.
Спектр сигнала 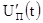 при этом равен
при этом равен
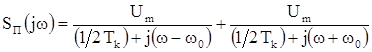 ,
,
где 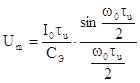 .
.
Ограничиваясь рассмотрением реальной частоты
спектра, найдем значение сигнала на выходе суммирующего оптимального фильтра.
Значение 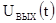 в момент
в момент 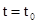 равно
равно
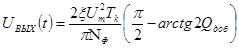 ,
,
где 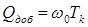 . Дисперсия шума на выходе оптимального фильтра определяется
. Дисперсия шума на выходе оптимального фильтра определяется
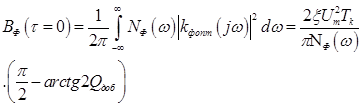 .
.
Нормируя
выражения 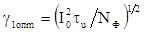 имеем следующее соотношение
имеем следующее соотношение
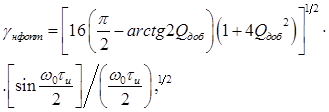
где 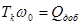 ,
, 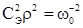 .
.
Исследуя
полученную зависимость на максимум по 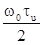 получим следующее, трансцедентное
уравнение
получим следующее, трансцедентное
уравнение
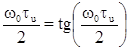
которое
имеет решение при 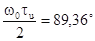 или
или 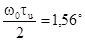 , тогда
, тогда
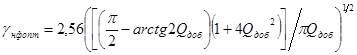 .
.
Суммарный
выигрыш в отношении сигнал/шум при этом равен
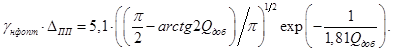
Исследуя
полученную зависимость на экстремум, имеем 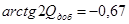 , тогда
, тогда 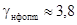 .
.
Таким образом, метод обработки сигнала с использованием внутренней
структуры сигнала в условиях преобразования огибающей
световой вспышки с последующей оптимальной фильтрацией приближает его по
эффективности к оптимальной обработке пакета световых импульсов и по отношению
к приему одиночного импульса увеличивает отношение сигнал/шум примерно в 3,8 раза. В фазоимпульсных лазерных системах
представляется возможным получить оценку временного положения импульса по
фазовым соотношениям сигнала в контурах ударного возбуждения с точностью
приближающихся к потенциальным возможностям фазовых систем при незначительных
потерях в амплитуде сигнала. Основное ограничение при экспериментальной
обработке результатов определяло влияние амплитуды отраженного сигнала на точность
измерения дистанции, так как время усреднения определялось декрементом
затухания сигнала в контуре ударного возбуждения и его амплитудой. Указанные
ограничения снимаются при введении
совокупности таких мер, как введение АРУ, применение цифровых фазовых
детекторов, нормировка числа анализируемых периодов колебаний сигнала, в фотоприемном тракте.
10.2. Фазоимпульсные датчики с
фиксацией дальности по
регистрации запаздывания отраженного импульса через изменения величины фазы
опорного канала
В данном методе момент излучения жестко
привязывается к фазе опорного колебания, а по моменту появления отраженного
импульса, фиксируется фазовый набег опорного сигнала. Оценка фазового набега
проводится по измерению амплитуда отраженного импульсного сигнала на выходе
фотоприемника при ее модуляции опорным сигналом на входе фотодетектора
(модуляционном фазовом детекторе) или по величине амплитуды опорного сигнала, отсчитанной
в момент прихода отраженного сигнала. В первом варианте высокочастотное
колебание частотой 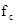 подается на делитель
частоты, формирующий импульсы для питания излучателя, и на модулирующий вход
фотоприемника (опорный канал), где осуществляется скачкообразное изменение фазы
частоты на
подается на делитель
частоты, формирующий импульсы для питания излучателя, и на модулирующий вход
фотоприемника (опорный канал), где осуществляется скачкообразное изменение фазы
частоты на 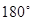 в такт с
частотой повторения импульсов
в такт с
частотой повторения импульсов 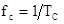 в соответствии с зависимостью
в соответствии с зависимостью
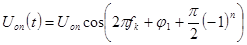 ,
,
где 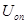 - амплитуда опорного сигнала,
- амплитуда опорного сигнала, 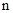 -
порядковый номер импульса. Напряжение на выходе фотоприемника
(модуляционно-фазового детектора) при этом равно
-
порядковый номер импульса. Напряжение на выходе фотоприемника
(модуляционно-фазового детектора) при этом равно
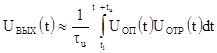 ,
,
где 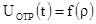 ;
; 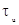 -
длительность импульса. Для прямоугольной формы импульса значение интеграла
можно представить при
-
длительность импульса. Для прямоугольной формы импульса значение интеграла
можно представить при 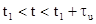 ,
, 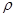 - коэффициент отражения.
- коэффициент отражения.
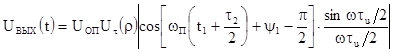 ,
,
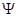 -
фазовый набег, и при
-
фазовый набег, и при 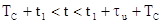
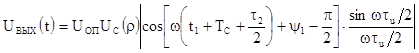 .
.
Из
расчетных данных следует, что на выходе модуляционно-фазового детектора имеет
место последовательность пар импульсом, отношение амплитуд которых не зависит
от отражающих свойств объекта и отличается на величину
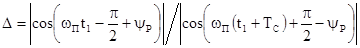 .
.
Форма импульса
представлена на рис.10.5. При наличии
отстройки по начальной фазе 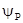 , если принять, что скачок фазы на
, если принять, что скачок фазы на 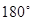 происходит при
условии
происходит при
условии 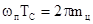 , где
, где 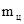 - число
фазовых циклов, тогда
- число
фазовых циклов, тогда
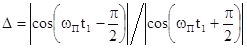 .
.
При 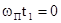 и
и 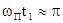 отношение
отношение 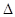 равно единице. Вычисление
отношения двух последующих импульсов требует применения запоминающих устройств
в виде пикового детектора с насыщенным тоновым ключом в цепи заряда, АЦП и
решающего устройства. Блок обработки может быть упрощен, если на выходе
фотоприемника использовать контур ударного возбуждения, преобразующего импульс
равно единице. Вычисление
отношения двух последующих импульсов требует применения запоминающих устройств
в виде пикового детектора с насыщенным тоновым ключом в цепи заряда, АЦП и
решающего устройства. Блок обработки может быть упрощен, если на выходе
фотоприемника использовать контур ударного возбуждения, преобразующего импульс 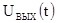 в затухающее
колебание.
в затухающее
колебание.
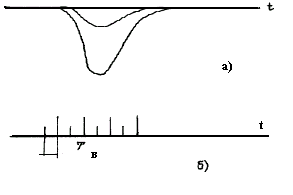
Число импульсов, измеренное по заданному
порогу, будет пропорционально логарифму отношения 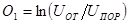 , где
, где 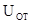 амплитудное значение
сигнала на выходе контура ударного возбуждения, значение которого в
значительном диапазоне частот равно
амплитудное значение
сигнала на выходе контура ударного возбуждения, значение которого в
значительном диапазоне частот равно 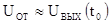 ;
; 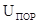 - пороговый уровень
отсчета. Разница колебаний в двух последующих импульсах с соответствующими амплитудами
затухающих колебаний
- пороговый уровень
отсчета. Разница колебаний в двух последующих импульсах с соответствующими амплитудами
затухающих колебаний 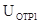 и
и 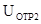 равна.
равна. 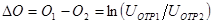 . Условие
. Условие 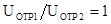 и
и 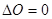 может быть положено в
основу для регистрации определенной дистанции. С точки зрения упрощения схемы обработки,
возможности регистрации фазового изменения непосредственно по амплитуде
результирующего сигнала перспективным является второй метод, в котором фазовый
набег фиксируется по величине амплитуды опорного сигнала, отсчитанной в момент
отраженного импульса. В данном методе
входным сигналом на величину его длительности выделяется часть опорного
гармонического сигнала, амплитуда которого определяется временным соотношением
опорного и входного сигналов. Сигнал на выходе инерционного дискриминатора для
данного метода можно представить
может быть положено в
основу для регистрации определенной дистанции. С точки зрения упрощения схемы обработки,
возможности регистрации фазового изменения непосредственно по амплитуде
результирующего сигнала перспективным является второй метод, в котором фазовый
набег фиксируется по величине амплитуды опорного сигнала, отсчитанной в момент
отраженного импульса. В данном методе
входным сигналом на величину его длительности выделяется часть опорного
гармонического сигнала, амплитуда которого определяется временным соотношением
опорного и входного сигналов. Сигнал на выходе инерционного дискриминатора для
данного метода можно представить
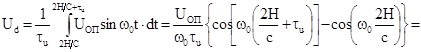
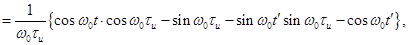
где 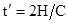 ;
; 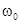 - частота опорного колебания.
- частота опорного колебания.
Функция
селекции по дальности 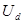 представляет
собой знакопеременную зависимость, повторяющую форму опорного сигнала:
представляет
собой знакопеременную зависимость, повторяющую форму опорного сигнала:
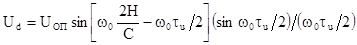 .
.
Так
как при 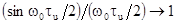 , то
, то 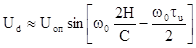 при
при 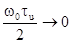 . Крутизна дискриминационной кривой при этом равна
. Крутизна дискриминационной кривой при этом равна
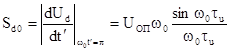 .
.
Отсчет
дальности в пределах одного фазового цикла, производится по алгоритму
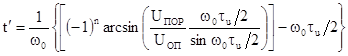
или с учетом принятых ограничений
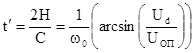
и вблизи нуля дискриминационной кривой эта зависимость
преобразуется к виду 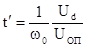 . Точность регистрации
временного положения импульса соответственно равна
. Точность регистрации
временного положения импульса соответственно равна
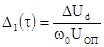 ,
,
где 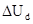 - погрешность измерения
амплитуды выделенного участка опорного сигнала в условиях изменения
длительности импульса и значений коэффициента отражения.
- погрешность измерения
амплитуды выделенного участка опорного сигнала в условиях изменения
длительности импульса и значений коэффициента отражения.
В системе отсчета длительность импульса,
когда имеет местостабилизация амплитуды входного сигнала,
местоположение нуля дискриминационной кривой не зависит от формы и амплитуды сигнала.
Так
как с высокой точностью стабилизировать амплитуду входного сигнала не
представляется возможным, необходимо рассмотреть погрешность 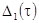 , обусловленную этим явлением, которая может быть оценена по
смещению центра импульса, измеренного по порогу отсчета. Расчетные данные
ошибки
, обусловленную этим явлением, которая может быть оценена по
смещению центра импульса, измеренного по порогу отсчета. Расчетные данные
ошибки 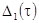 для некоторых форм
импульса приведены в табл.10.1.
для некоторых форм
импульса приведены в табл.10.1.
Погрешность
|
Экспоненциальная форма
|
Прямоугольная форма
|
Колоколообразная форма
|
|
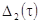 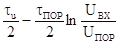 0 0 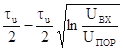
|
|
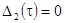 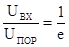 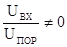 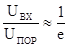
|
Таблица 10.1. Расчетные
данные ошибки
Оценку
условия однозначного измерения для данного метода рассмотрим при 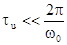 . В этом случае
. В этом случае
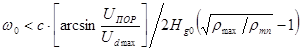 ,
,
где 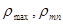 -
максимальное и минимальное значение коэффициента рассеяния. Учитывая, что
измерение должно проводиться в пределах одного полупериода
-
максимальное и минимальное значение коэффициента рассеяния. Учитывая, что
измерение должно проводиться в пределах одного полупериода 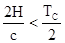 , где
, где 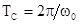 .Частота опорного сигнала, с одной стороны, ограничена
требованием по устранению неоднозначности, а с другой - условием привязки измерения
.Частота опорного сигнала, с одной стороны, ограничена
требованием по устранению неоднозначности, а с другой - условием привязки измерения 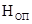 к определенному
участку дискриминационной кривой, тогда необходимое значение
к определенному
участку дискриминационной кривой, тогда необходимое значение 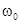 может быть выбрано на
основании следующего неравенства
может быть выбрано на
основании следующего неравенства
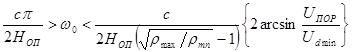 .
.
В условиях выбранного значения 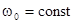 необходимо определить
требование по длительности импульса
необходимо определить
требование по длительности импульса 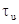 , которое определяется
на основе решения задачи по обеспечения потенциальной точности
, которое определяется
на основе решения задачи по обеспечения потенциальной точности 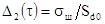 , где
, где 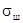 среднее квадратичное значение флуктуаций на выходе
дискриминатора. Для обеспечения максимальной крутизны дискриминатора
среднее квадратичное значение флуктуаций на выходе
дискриминатора. Для обеспечения максимальной крутизны дискриминатора 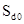 необходимо
стремиться к сокращению
необходимо
стремиться к сокращению 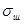 . С другой стороны,
уменьшение
. С другой стороны,
уменьшение 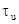 приводит к увеличению
приводит к увеличению 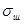 , что противоречит
условию получения максимальной точности
, что противоречит
условию получения максимальной точности 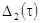 . Дисперсия флуктуаций
на выходе преобразователя
. Дисперсия флуктуаций
на выходе преобразователя 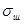 зависит от параметров
схемы построения
зависит от параметров
схемы построения 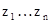 и шумов фотоприемного тракта
и шумов фотоприемного тракта 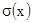 , то есть
, то есть
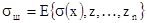 .
.
Учитывая
независимость воздействия указанных параметров на 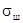 , задачу по определению
условия обеспечения потенциальной точности разбивают на два этапа: проведение
исследований по влиянию параметров фотоприемного
тракта на точность измерения временного интервала, в этом случае условие
, задачу по определению
условия обеспечения потенциальной точности разбивают на два этапа: проведение
исследований по влиянию параметров фотоприемного
тракта на точность измерения временного интервала, в этом случае условие 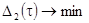 может быть оценено при
минимизации
может быть оценено при
минимизации 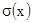 ; выбор параметров схемы построения дискриминатора из условия
; выбор параметров схемы построения дискриминатора из условия
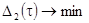 . Для минимизации
. Для минимизации 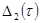 воспользуемся
значением
воспользуемся
значением 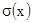 , полученным при обнаружении сигнала. При согласованном
приемнике
, полученным при обнаружении сигнала. При согласованном
приемнике 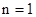 и
и 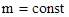 значение
значение 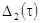 представим
представим
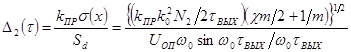 ,
,
где 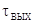 -
длительность импульса на входе дискриминатора. Исследуя полученное выражение на
экстремум по
-
длительность импульса на входе дискриминатора. Исследуя полученное выражение на
экстремум по 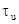 при
при 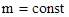 , получим следующее выражение
, получим следующее выражение 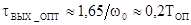 , где
, где 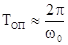 - период опорной
частоты. Поскольку длительность импульса на выходе инерционного звена фотодетектора
определяется зависимостью
- период опорной
частоты. Поскольку длительность импульса на выходе инерционного звена фотодетектора
определяется зависимостью 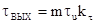 , где
, где 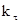 коэффициент, учитывающий
изменение длительности в зависимости от уровня отсчета,
коэффициент, учитывающий
изменение длительности в зависимости от уровня отсчета, 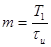 то ошибка, обусловленная шумовой составляющей
то ошибка, обусловленная шумовой составляющей 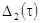 , может быть представлена.
, может быть представлена.
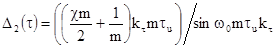 .
.
При отсчетах 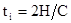 в области
в области 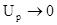 можно считать, что
можно считать, что 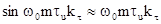 . В этом случае
. В этом случае 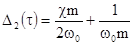 . Минимальное значение
. Минимальное значение 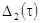 реализуется при
реализуется при 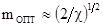 . Совпадение условий
реализаций максимального отношения сигнал/шум (
. Совпадение условий
реализаций максимального отношения сигнал/шум (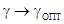 при
при 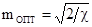 и минимальной ошибки
и минимальной ошибки 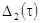 является специфической
особенностью рассматриваемой схемы обработки
сигнала. Полученные соотношения позволяют определить и рациональные варианты
построения фотоприемиого тракта, обеспечивающие
минимум ошибки
является специфической
особенностью рассматриваемой схемы обработки
сигнала. Полученные соотношения позволяют определить и рациональные варианты
построения фотоприемиого тракта, обеспечивающие
минимум ошибки 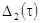 . Очевидно, что
. Очевидно, что 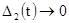 , когда
, когда 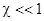 или когда шумы на
выходе фотодетектора будут существенно меньше шумов усилительного тракта, а
коэффициент усиления инерционного фотодетектора существенно больше коэффициента
усиления усилителя, что соответствует известному положению о реализации
минимальных приведенных шумов тракта. Такое соотношение реализуется при
использовании фотодетектора со значительным квантовым выходом, большим
внутренним усилением и наличием интерференционного фильтра на входе приемника.
В этом случае шумы усилительного тракта являются основным препятствием по
сокращению
или когда шумы на
выходе фотодетектора будут существенно меньше шумов усилительного тракта, а
коэффициент усиления инерционного фотодетектора существенно больше коэффициента
усиления усилителя, что соответствует известному положению о реализации
минимальных приведенных шумов тракта. Такое соотношение реализуется при
использовании фотодетектора со значительным квантовым выходом, большим
внутренним усилением и наличием интерференционного фильтра на входе приемника.
В этом случае шумы усилительного тракта являются основным препятствием по
сокращению 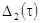 . Дальнейшее сокращение ошибки
. Дальнейшее сокращение ошибки
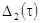 связано с потерей
энергии сигнала. В этом случае поиск рациональных параметров схемы
дискриминатора должен проводиться при совместном решении вопросов, связанных с
обеспечением условия
связано с потерей
энергии сигнала. В этом случае поиск рациональных параметров схемы
дискриминатора должен проводиться при совместном решении вопросов, связанных с
обеспечением условия 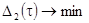 и получением минимальных потерь амплитуды
сигнала, то есть
и получением минимальных потерь амплитуды
сигнала, то есть
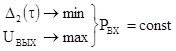 .
.
При
анализе огибающей импульсов на выходе фотодетектора следует, что длительность
фронта менее подвержена изменению при отклонении параметров фазового детектора.
Поэтому наиболее приемлемым решением является введение операции дифференцирования. Испытания изготовленного образца в камере
туманов, на стенде вертикальных опусканий показали, что при выборе частоты
опорного колебания 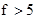 мГц можно реализовать помехозащищенный
датчик к действию туманов, дымов с
мГц можно реализовать помехозащищенный
датчик к действию туманов, дымов с 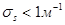 . При этом пропуски объекта имеют место при
. При этом пропуски объекта имеют место при 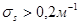 и нерешенным вопросом
здесь остается обеспечение помехоустойчивости к действию продуктов плотной пыли
и стеклянных микросфер.
и нерешенным вопросом
здесь остается обеспечение помехоустойчивости к действию продуктов плотной пыли
и стеклянных микросфер.
10.3. Вобуляционный
метод измерения
дистанции
С точки зрения сокращения времени теплового
разогрева ПКГ можно при непрерывном излучении использовать сигнал с крутым фронтом
и срезом. В этом плане желательно использовать метод дальнометрии
с модуляцией по определенному закону периода или длительности зондирующих
импульсов. Поэтому сочетание поляризационного метода с вобуляционным
может дать дополнительный выигрыш в методах обнаружения и регистрации объектов
на железнодорожном транспорте. Наибольшее практическое применение находит вобуляция периода. Если излучение промодулировано
прямоугольными импульсами с изменяющимся периодом, то результирующий спектр
пачки сигналов огибающей можно представить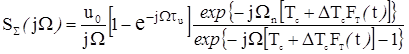 ,
,
где 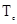 -
начальное значение периода повторения импульсов;
-
начальное значение периода повторения импульсов; 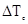 -
вобуляция периода повторения;
-
вобуляция периода повторения; 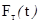 - функция изменения периода повторения
модулирующего сигнала. Квадрат модуля спектра огибающей равен
- функция изменения периода повторения
модулирующего сигнала. Квадрат модуля спектра огибающей равен
 .
.
Спектр состоит из серии
узких спектров с огибающей
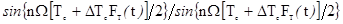 .
.
Ширина полосы прозрачности
каждого узкополосного спектра (кроме первого) равна 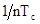 , число, спектров в
наборе
, число, спектров в
наборе 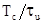 . С увеличением числа
импульсов в интервале модуляции полоса прозрачности каждого узкополосного
спектра сужается. Суммарная полоса прозрачности равна
. С увеличением числа
импульсов в интервале модуляции полоса прозрачности каждого узкополосного
спектра сужается. Суммарная полоса прозрачности равна
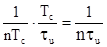 .
.
При изменении
периода повторения по времени узкополосный спектр соответственно смещается
относительно 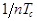 в соответствии с
заданным законом модуляции. Применительно к выбранному методу дальнометрии рассмотрим модуль спектра огибающей
отраженного сигнала
в соответствии с
заданным законом модуляции. Применительно к выбранному методу дальнометрии рассмотрим модуль спектра огибающей
отраженного сигнала
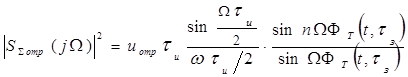 ,
,
где
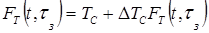 .
.
При относительно
большом интервале изменения вобуляции 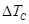 , определяемом количеством n импульсов за период изменения
функции F(t), представляется возможным
выбором
, определяемом количеством n импульсов за период изменения
функции F(t), представляется возможным
выбором 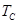 достичь уровня, когда
достичь уровня, когда 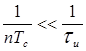 , то есть, когда полосу узкого спектра можно принять за
квазигармоническое колебание с изменяющейся частотой по закону
, то есть, когда полосу узкого спектра можно принять за
квазигармоническое колебание с изменяющейся частотой по закону
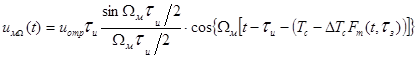 ,
,
где m -
номер гармонических составляющих в спектре 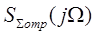 , отстоящих друг от друга на величину
, отстоящих друг от друга на величину 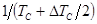 . Длительность импульса выбирается из условия получения
заданного числа гармонических составляющих и в большинстве случаев принимается
. Длительность импульса выбирается из условия получения
заданного числа гармонических составляющих и в большинстве случаев принимается 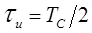 , а m = 1, тогда
, а m = 1, тогда
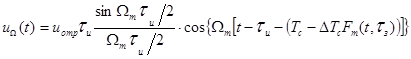 .
.
Аналогично может быть представлена и огибающая
излученного сигнала
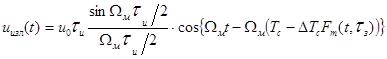 ,
,
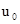 - амплитуда сигнала.
- амплитуда сигнала.
С учетом принятых ограничений результирующий
сигнал, получаемый в результате смешивания составляющих 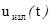 и
и 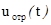 в прикатодной
области ФЭУ с последующим
выделением разностной частоты можно представить
в прикатодной
области ФЭУ с последующим
выделением разностной частоты можно представить
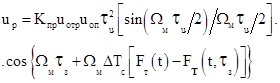
или
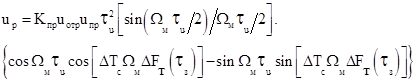 , (10.5)
, (10.5)
где 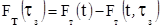 .
.
Описанные соотношения хорошо
совпадают с выражениями, полученными для частотно-модулированного сигнала.
Выражение отражает интегральный метод обработки. Здесь значение 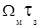 характеризует допплеровскую составляющую
характеризует допплеровскую составляющую
 ,
,
где 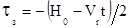 , Н0 - точка появления отраженного
сигнала, а
, Н0 - точка появления отраженного
сигнала, а 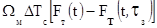 определяет частоту биений, получаемую в результате вобуляции периода модулирующей функции при выделении
разностной частоты.
определяет частоту биений, получаемую в результате вобуляции периода модулирующей функции при выделении
разностной частоты.
Зависимость является
также исходным соотношением для спектрального анализа результирующего сигнала.
Если принять, что вобуляция периода осуществляется по
закону 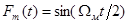 , то
, то
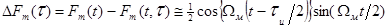 .
.
Учитывая, что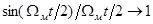 , значение
, значение 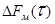 равно
равно
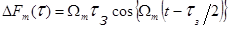 .
.
С учетом
изложенного получаем следующее выражение
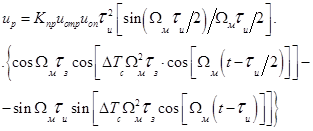
Разлагая составляющие
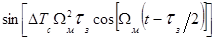
и
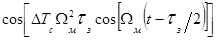
в ряд по
функциям Бесселя, получим следующее окончательное выражение
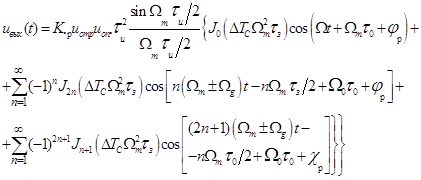 ,
,
где 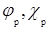 -
постоянные фазовых набегов. Таким образом, спектр результирующего сигнала
близок к спектру сигнала, рассмотренного в предыдущем разделе. Отличительной
особенностью является то, что аргумент функций Бесселя, определяющий характер
изменения амплитуд гармонических составляющих по дистанции, зависит от величины
вобуляции частоты модуляции и времени задержки
-
постоянные фазовых набегов. Таким образом, спектр результирующего сигнала
близок к спектру сигнала, рассмотренного в предыдущем разделе. Отличительной
особенностью является то, что аргумент функций Бесселя, определяющий характер
изменения амплитуд гармонических составляющих по дистанции, зависит от величины
вобуляции частоты модуляции и времени задержки 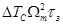 . Помехозащищенность
здесь определяется выбором длительности зондирующего импульса и конструктивными
решениями по формированию "мертвой зоны" ПРУ.
. Помехозащищенность
здесь определяется выбором длительности зондирующего импульса и конструктивными
решениями по формированию "мертвой зоны" ПРУ.