9. Фазовые системы ближней дальнометрии
Проблема высокоточных измерений в системах ближней дальнометрии может
быть решена за счет использования полупроводниковых квантовых генераторов с
непрерывным излучением и использования фазовых методов дальнометрии, обладающих
наилучшими потенциальными возможностями по снижению потенциала системы и
дисперсии ошибки измерения дальности. Фазовые системы обладают наилучшими
возможностями по реализации наименьших габаритных и весовых характеристик, как
будет показано, имеют относительно не плохие решения по обеспечению высокой
помехоустойчивости при действии аэрозольных помех естественного и искусственного
происхождения. Однако отсутствие обоснованных решений и экспериментальных
исследований препятствует широкому использованию их в практику проектирования
таких систем. Из всего многообразия решений [166-151]остановимся лишь на наиболее
оригинальных методах обработки сигнала и вопросах обеспечения помехозащиты.
9.1.Энергетический расчет и
реализация потенциальных возможностей в фазовых системах дальнометрии
9.1.1.
Энергетический расчет
Энергетический расчет является одним из основополагающих вопросов
проектирования лазерных систем дальнометрии, использующих в качестве излучателя
полупроводниковые лазеры с непрерывным излучением. При обосновании и проведении
расчетов будем использовать следующие определения. За пороговую чувствительность
принимается минимальная мощность, достаточная для регистрации объекта,
расположенного на максимальной дальности при отношении сигнал/шум, определяемом
заданной вероятностью ложных срабатываний системы.
За потенциал принимается отношение мощности излучения полупроводникового
лазера к пороговой чувствительности дальномерной системы в логарифмическом
масштабе (П = 10lg(Po/Pпор)), необходимой для достоверной регистрации дистанции
до объекта. Вычисление требуемой мощности лазерного излучения будем рассматривать
для случаев накопления (суммирования)
отраженного сигнала и без него. Операция суммирования для фазометрических
систем связана с оцифровкой принятой информации через определенный шаг
дискретизации, например 10 нс и суммированием на i–тых интервалах при каждом цикле обзора пространства , равном периоду
следованию гармонического сигнала, соответствующему циклу однозначного отсчета.
Применение операции накопления (суммирования) позволяет улучшить отношение
сигнал-шум в Ö N, где N-число накапливаемых импульсов. Это
увеличение сопровождается суммированием сигнала в соответствующей пропорции.
Это также приводит к уменьшению шумов, которые в силу того, что имеют разную
полярность, появляются от опроса к опросу в каждой I-той выборке по случайному закону. Влияние процесса накопления будем
учитывать при формировании пороговой чувствительности всей системы. В таких
системах используется, как правило, фазовое цифровое фазовое детектирование,
когда искомая фаза находится как временной интервал, фиксируемый между
характерными точками оцифрованных и занесенных в память опорного и отраженного
гармонических сигналов. Принятая мощность от объекта, расположенного на
дистанции Н от дальномера при изотропном эквиваленте определяется зависимостью
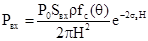 , (9.1)
, (9.1)
P0 - мощность излучателя; Sвх = pr2 - площадь входного зрачка приемного
объектива ; 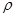 - коэффициент отражения
объекта; fc(Q) - коэффициент, учитывающий индикатрису рассеяния и
поправку к изотропному эквиваленту рассеяния; ss - коэффициент объемного рассеяния;
Н -
дистанция до объекта.
- коэффициент отражения
объекта; fc(Q) - коэффициент, учитывающий индикатрису рассеяния и
поправку к изотропному эквиваленту рассеяния; ss - коэффициент объемного рассеяния;
Н -
дистанция до объекта.
Мощность излучения найдем, приравняв Рвх
к пороговой чувствительности системы, за которую принимаем
 ,
(9.2)
,
(9.2)
где
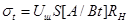 - средне квадратичное значение теплового шума,
приведенного ко входу; Uш[B/ÖГц] - плотность теплового шума малошумящего усилителя по паспорту (например,
4 нв/ÖГц); sдр - средне квадратичное значение дробового шума; g - превышение сигнала над шумами (отношение сигнал/шум), определяемое из
требований по заданной вероятности ложных срабатываний системы по порогу
квантования; S[A/Bt] - ампер-ваттовая характеристика фотодиода, как единица
преобразования входной мощности в ток; RH - сопротивление нагрузки фотодиода в вентильном режиме
включения; Мх - коэффициент лавинного умножения фотодиода; N -количество накапливаемых импульсов в каждом I-том интервале оцифровки. В свою очередь Ösдр = (2eDfPфS[А/Вт]MxRн2)1/2 - среднеквадратичное значение дробового шума; е- заряд электрона; Df = 0.25/tи - оптимальная полоса
пропускания фотоприемника; tи - длительность импульса; х - показатель степени при коэффициенте М (для
германиевого фотодиода х=3, для кремниевого х = 2,4); Pф = (E0WrSвхfc(Q)Dl)/(2p) – мощность солнечной фоновой засветки; Dl - оптическая полоса приема; Еф [Вт/ м3]
- плотность прямого солнечного
фона; W [рад] - телесный угол визирования приемного объектива; r - коэффициент отражения подстилающей поверхности; Sвх = pr2 - площадь входного зрачка приемного объектива. При вычислении
пороговой мощности произведение корня из
суммы дисперсий на отношение сигнал/шум, приравниваем к пороговому значению
полезного сигнала, который линейно связан с коэффициентом умножения. Поэтому в
знаменателе введена линейная вольт-ваттовая характеристика как функция от М:
- средне квадратичное значение теплового шума,
приведенного ко входу; Uш[B/ÖГц] - плотность теплового шума малошумящего усилителя по паспорту (например,
4 нв/ÖГц); sдр - средне квадратичное значение дробового шума; g - превышение сигнала над шумами (отношение сигнал/шум), определяемое из
требований по заданной вероятности ложных срабатываний системы по порогу
квантования; S[A/Bt] - ампер-ваттовая характеристика фотодиода, как единица
преобразования входной мощности в ток; RH - сопротивление нагрузки фотодиода в вентильном режиме
включения; Мх - коэффициент лавинного умножения фотодиода; N -количество накапливаемых импульсов в каждом I-том интервале оцифровки. В свою очередь Ösдр = (2eDfPфS[А/Вт]MxRн2)1/2 - среднеквадратичное значение дробового шума; е- заряд электрона; Df = 0.25/tи - оптимальная полоса
пропускания фотоприемника; tи - длительность импульса; х - показатель степени при коэффициенте М (для
германиевого фотодиода х=3, для кремниевого х = 2,4); Pф = (E0WrSвхfc(Q)Dl)/(2p) – мощность солнечной фоновой засветки; Dl - оптическая полоса приема; Еф [Вт/ м3]
- плотность прямого солнечного
фона; W [рад] - телесный угол визирования приемного объектива; r - коэффициент отражения подстилающей поверхности; Sвх = pr2 - площадь входного зрачка приемного объектива. При вычислении
пороговой мощности произведение корня из
суммы дисперсий на отношение сигнал/шум, приравниваем к пороговому значению
полезного сигнала, который линейно связан с коэффициентом умножения. Поэтому в
знаменателе введена линейная вольт-ваттовая характеристика как функция от М: 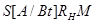 .
.
За условие обеспечения оценки местоположения
цели в условиях прямой видимости принимается ослабление при законе Бугера
exp(-2ssHmax)
= exp(-3.9) = 0.02, где H 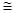 V =3,9/ss определяется формулой видимости объектов в атмосфере,
Hmax -
максимальная дальность до объекта измерения, ss – коэффициент рассеяния. То есть запас по мощности
изучения должен составлять по отношению к раcсчитанному потенциалу как минимум 50 раз. С учетом представленных
данных определяем необходимую мощность
излучения для условия применения германиевого лавинного фотодетектора и без
учета ослабления сигнала в аэрозольной среде
V =3,9/ss определяется формулой видимости объектов в атмосфере,
Hmax -
максимальная дальность до объекта измерения, ss – коэффициент рассеяния. То есть запас по мощности
изучения должен составлять по отношению к раcсчитанному потенциалу как минимум 50 раз. С учетом представленных
данных определяем необходимую мощность
излучения для условия применения германиевого лавинного фотодетектора и без
учета ослабления сигнала в аэрозольной среде
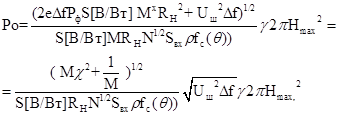 (9.3)
(9.3)
где
 ¾
¾
отношение
среднеквадратичных дробовых и тепловых шумов.
Из представленной зависимости для Р0
следует, что минимальное значение мощности зависит от коэффициента лавинного
умножения и от параметра c. Оптимальное
значение коэффициента лавинного умножения М при котором необходимая для срабатывания
системы мощность Ро минимальна найдем
дифференцируя зависимость Р0=f(M,c) по М и приравнивая производную к нулю. В
результате имеем: Моптим(c) = (2/(c2(x-2)))1/x. График Моптим(c) приведен на рис.9.1.
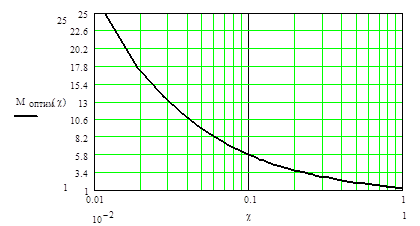
Рис.9.1. График зависимости оптимального
значения коэффициента лавинного умножения М от c, при
которых необходимая для
срабатывания мощность
Ро минимальна
Чем меньше дробовые шумы по отношению к тепловым (меньше значение c), тем
больше требуется увеличить коэффициент лавинного умножения, при котором
реализуется минимальная мощность излучения. Учитывая, что максимальное значение
для лавинного фотоприемника коэффициент умножения примерно ограничен паспортным
значением 17,то можно отметить, что процесс адаптации приемника в условиях
изменяющегося фона может достигать до значений c=0.02.
Построим график зависимости коэффициента умножения M(Uсм) для
наиболее типового лавинного фотодиода ЛФД-2 от напряжения смещения Uсм.
Коэффициент умножения лавинного фотодиода М может быть представлен эмпирической
формулой Миллера]:
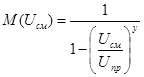 , y=2-6, (9.4)
, y=2-6, (9.4)
где Uпр – напряжение пробоя лавинного фотодиода. Согласно
паспортных данных, например для ЛФД-2, M(19.8) = 10 и M(20.2) =
17. Подставляя эти данные в (9.4) находим:
 и
и 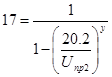 ,
,
где Uпр1 и Uпр2–
напряжения пробоя лавинного фотодиода при M(19.8)=10 и M(20.2)=17
соответственно. Решая эти уравнения относительно Uпр1 и Uпр2 находим:
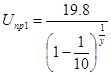 и
и 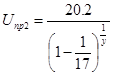 .
.
Найдем значение y при котором Uпр1=Uпр2=Uпр
графически. Для этого построим графики зависимостей Uпр1 и Uпр2 от y/ Из рис.9.2. находим, что Uпр1=Uпр2= Uпр=20.8 при
y=2.2. На основе полученных
данных найдем график зависимости коэффициента
умножения M(Uсм) ЛФД-2
от напряжения смещения Uсм (рис.9.3.).
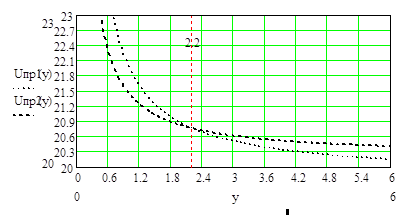
Рис.9.2.
Графики зависимостей Uпр1 и Uпр2 от y
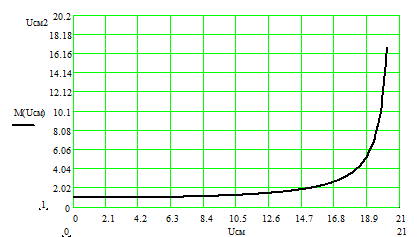
Рис.9.3..
График зависимости коэффициента умножения M(Uсм) ЛФД-2 от напряжения
смещения Uсм
Таким образом, получен характер зависимости изменения коэффициента
лавинного умножения от напряжения смещения. Для выбранного значения полученные расчеты хорошо совпадают с паспортными
данными ЛФД-2. Так для реализации максимального паспортного
значения коэффициента умножения М = 17 требуется напряжения порядка 20.2, а для
коэффициента умножения 10- напряжение 19,8В, что совпадает с паспортными
данными.
Приведем
пример энергетического расчета. Пусть фазовый дальномер рассчитан на дальность Hmax =
2000м, Df
= 1кГц. Расчет проведем для случая применения лавинного фотоприемника типа ЛФД-2 при следующих начальных
условиях: Dl = 20*10-10-оптическая
полоса приемника; Еф-0.1*10-10 Вт/ м3 -
плотность прямого солнечного фона; W
[рад] = 0,03 рад- телесный угол визирования приемного объектива; r=0.4 - максимальный коэффициент отражения
подстилающей поверхности; Sвх=pr2 =p4×10-4м2
- площадь входного зрачка
приемного объектива; Rн = 6800Ом –сопротивление нагрузки; S[A/Вт] = 0.82 - ампер-ваттовая характеристика
фотодиода; M- коэффициент лавинного
умножения фотодиода; x=3 для германиевого
фотодиода; Ut = 3*10-9(Df)1/2
– приведенное напряжение шума усилителя; Df-
полоса приемного усилительного тракта. Максимально возможное количество
накапливаемых импульсов Nmax
ограничивается требованием однозначного измерения дальности, то есть период
колебаний равен времени прохождения импульса от дальномера до объекта измерения
и обратно. Принимая в виду, что максимальное время взаимодействия с объектом
измерения для непрерывного лазера обычно составляет 1 с, вычислим Nmax, равное числу периодов: Nmax = fc= с/(2Нmax) =75000. Пользуясь выражением для P0
построим график зависимости понижения мощности излучения P0(M,N), необходимой для
срабатывания дальномера при отношении сигнал/шум 2 в зависимости от числа
накапливаемых импульсов при различных М. Здесь
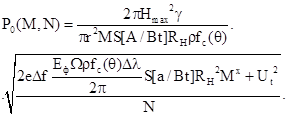
Результат
представлен на рис. 9.4. Из
представленной зависимости следует, что даже без накопления (N=1) мощность излучения лазеров с непрерывным
излучением находится пределах технических требований на серийные ПКГ. Введение
лавинного умножения при N=1
уменьшает мощность излучения с 1 до 0,4 Вт. Применение цифровой обработки
сигнала с накоплением мощность излучения до 10мВт, что делает такой дальномер
экологически безопасным для зрения. Мощность излучения не линейно зависит от
коэффициента умножения М (рис.9.5.) и минимальна при М=4 не зависимо от
накопления информации или без неё.
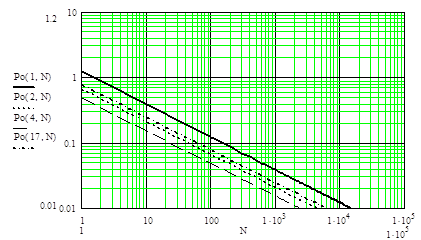
Рис.9.4.
Изменение мощности излучения, необходимой для
регистрации
объекта, расположенного на дальности 2000м
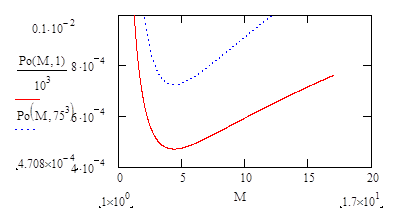
Рис. 9.5.
Изменение мощности излучения от коэффициента умножения М
Для того чтобы увидеть как влияет величина
дробовых шумов на g введем отношение среднеквадратичных значений
дробовых и тепловых шумов c = Uдр/Uт как
функцию c = f(Pф), c0 = Uдр/Uт- при коэффициенте
лавинного умножения М = 1 и максимально фоновой засветки при Dl=20 10-10м. Найдем
соотношение сигнал/шум:
g = (РпорS[А/Rн)/(((cо2Mx-2+M-2)/N)1/2Uт). (9.5)
Графики зависимостей соотношения сигнал/шум g(М,c,N) от коэффициента лавинного
умножения при различных c для систем с непрерывным лазером приведен на рис.9.6.. Здесь
уменьшение c по отношению к
отображает уменьшение фоновой засветки, например при ухудшении погодных
условий.
За
c0 принимаем
отношение дробовых и тепловых шумов при М=1
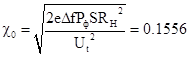 ,
,
которое
характеризует отношение дробовых шумов к тепловым при максимальных значений
фоновой засветки (для принятых параметров системы) и минимальных дробовых
шумов, определяемых схемой усилительного тракта.
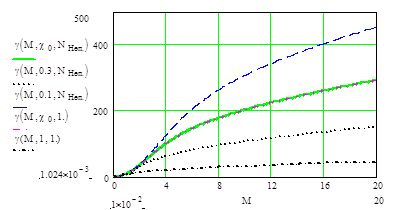
Рис. 9.6.
Графики зависимостей соотношения сигнал/шум g(М,c,N) от коэффициента лавинного умножения М при различных
c для систем с непрерывным
лазером, c0=0.1556 –
наихудшее
для
выбранного дальномера значениеc.
При уменьшении c повышается g. Физически это происходит
из-за того, что при естественном уменьшении фоновой засветки дробовые шумы
уменьшаются и сокращается, соотвeтственно, c и можно в этой ситуации увеличивать
коэффициент умножения лавинного фотодетектора, увеличивая в соответствующей
пропорции как сигнал и так и шум и так до тех пор пока не наступит оптимум отношения
сигнал/шум. Это происходит, как правило, вблизи значений М, когда дробовые шумы
приравниваются к тепловым. Отсюда и получаемый выигрыш в отношении сигнал-шум
при уменьшении c. Кроме того, можно сделать
вывод, что для обеспечения оптимума соотношения сигнал/шум в тракте усиления с
применением ЛФД нужно вводить автоматическую регулировку усиления по шумам,
которые изменяются в основном от уровня фоновой засветки и регулируются
коэффициентом умножения. Необходимую для срабатывания системы мощность с учетом только дробовых и
тепловых шумов находим используя выражение для c:
Ро = (gнеоб.2pDmax2Uт(c2Mx-2+M-2)/N)1/2)/(S[А/Вт]RнSвхrfc(Q)).
(9.6)
Графики
зависимостей Ро от коэффициента лавинного умножения при различных c для систем с непрерывным лазером приведены на рис.9.7
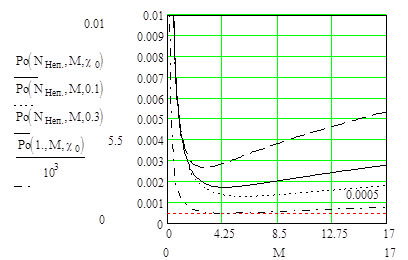
Рис.9.7..
Графики зависимостей Ро(N,M,c) от коэффициента лавинного
умножения М при различных c для систем с непрерывными
лазерами, c0 = 0.1556
–расчетное наихудшее значение c.
Из рис.9.7 следует, что оптимальное значение коэффициента лавинного
умножения М, при котором необходимая для срабатывания системы мощность Ро
минимальна зависит от c. Для наихудших условий, т.е.
максимально фоновой засветке без накопления мощность излучения, необходимая для
регистрации объекта на дистанции 2000м составляет порядка 0,5 Вт, а при
накоплении 1,8 мВт. Найдем зависимость Р0 = f(c),
дифференцируя по М и приравнивая производную к нулю. В результате имеем: Моптим(c) =
(2/(c2(x-2)))1/x. Для того чтобы найти минимально
возможную, необходимую для срабатывания системы мощность Р0 найдем
зависимость Р0 = f(c,Моптим). Подставив
выражение для Моптим) построим график
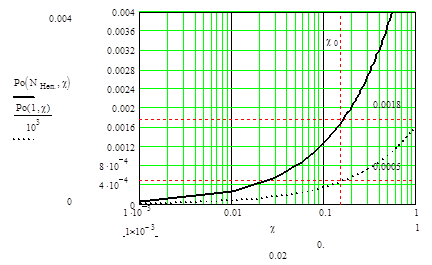
Рис.9.8. График
зависимости оптимальной мощности ¾Ро(N,c) от c и----
Ро(1,c) от c для
систем с непрерывным лазером.
Пользуясь рис.9.7 и рис. 9.8 можно сделать вывод, что при накоплении и
уменьшении c можно снизить необходимую для срабатывания системы
мощность Р0, но при этом требуется соответственно поднимать
коэффициент лавинного умножения М. Полученный график подтверждает раннее
определённые данные по мощности излучения. Значение потенциала системы не
зависит от наличия процедуры накопления и равно
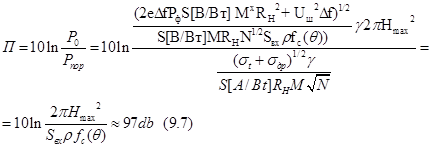
9.1.2. Реализация
потенциальных возможностей
Если приемный тракт представить как
квазиоптимальный фильтр или коррелятор, то увеличение дальности действия
дальномера связано с увеличением энергии зондирующего сигнала. Существенного
увеличения энергии при ограниченной пиковой мощности излучателя удается при
переходе к непрерывному режиму. Длительность выборки отраженного сигнала
определяется требованиями, накладываемыми на инерционность измерительной системы.
Поэтому фазовые методы дальнометрии кроме высокой точности измерений дистанции
реализуют регистрацию дистанции при тех же энергиях, что и в других методах
дальнометрии, но в относительно узкой полосе приема. В фазовых методах
дальнометрии при амплитудной модуляции излучения информация о дистанции
извлекается в аналоговом и цифровом фазовых детекторах по фазовой задержке модулирующего
отраженного и опорного колебания. Аналоговый фазовый детектор представляет
коррелятор опорного и отраженного сигналов, в котором отраженный сигнал по отношению к опорному
меняет задержку в зависимости от дальности до объекта. В качестве
результирующей корреляционной функции выступает
дискриминационная характеристика фазового детектора. Здесь разность фаз
между опорным и принятым сигналами, т.е. фазовая задержка выступает как
дальность до объекта. Фазовый цикл однозначного отсчета аналогового фазового
дискриминатора представляет знакопеременную функцию в пределах -p/2¸+p/2. Наличие инерционного звена
на выходе фазового детектора (сумматор- интегратор произведения) позволяет
проводить накопление сигнала и подавление
шума, ели время выборки или время
фазовой задержки существенно превышает время одноразовой дискриминации. Эта
операция тем самым позволяет повысить
пороговую чувствительность системы в целом.
При фиксации максимума огибающей полезных сигналов при действии шумов ,
представляющих аддитивную смесь, дисперсия ошибки регистрации равна
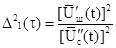 ,
,
где 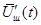 - производная шумового процесса,
- производная шумового процесса, 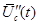 -
вторая производная по сигналу. После соответствующих преобразований приходим к
известному положению, когда потенциальная точность локационных систем
определяется
-
вторая производная по сигналу. После соответствующих преобразований приходим к
известному положению, когда потенциальная точность локационных систем
определяется 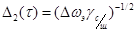 , где Dwэ - эквивалентная ширина спектра. При заданном отношении сигнал/шум значение D2(t)
определяется параметром
, где Dwэ - эквивалентная ширина спектра. При заданном отношении сигнал/шум значение D2(t)
определяется параметром
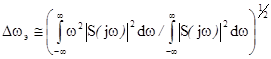 ,
,
где w- частота
спектра сигнала на выходе фотодетектора. Форма спектра с эффективной его
шириной представляет фигуру симметричную относительно центральной частоты 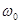 . По аналогии с механикой формула эффективной ширины спектра
выражает центральный момент инерции описанной фигуры. Как известно, момент
инерции максимален, когда вся «масса» фигуры сосредоточена на краях заданного
участка, то есть когда спектр сигнал состоит из двух гармонических составляющих w1 и w2 ,
разделенных интервалом Dw, что соответствует
условию реализации фазовых методов дальнометрии.
Этот вывод справедлив и для одночастотных методов, если фазовый сдвиг одной из
них приравнять нулю. Фазовый
метод измерения дальности является наилучшим в тех случаях, когда наблюдение
заведомо ограничено одним объектом.
. По аналогии с механикой формула эффективной ширины спектра
выражает центральный момент инерции описанной фигуры. Как известно, момент
инерции максимален, когда вся «масса» фигуры сосредоточена на краях заданного
участка, то есть когда спектр сигнал состоит из двух гармонических составляющих w1 и w2 ,
разделенных интервалом Dw, что соответствует
условию реализации фазовых методов дальнометрии.
Этот вывод справедлив и для одночастотных методов, если фазовый сдвиг одной из
них приравнять нулю. Фазовый
метод измерения дальности является наилучшим в тех случаях, когда наблюдение
заведомо ограничено одним объектом.
9.
2. Принципы фазовой дальнометрии
Сущность измерения дистанции фазовыми методами дальнометрии определяется
фазовым сдвигом, определяемым между опорным и отраженным модулирующим сигналом.
Взаимосвязь такого фазового сдвига с измеряемой дальностью можно получить из
рисунка 9.9.

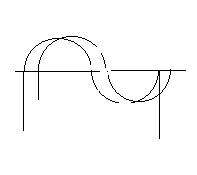
Составим
пропорцию 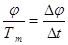 . Отсюда в градусном исчислении получим основополагающую формулу
. Отсюда в градусном исчислении получим основополагающую формулу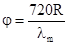 . Соответственно, погрешность измерений определяется
. Соответственно, погрешность измерений определяется 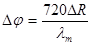 . Из этих двух выражений имеем пропорцию
. Из этих двух выражений имеем пропорцию 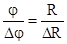 . Т.е. при заданной относительной погрешности измерения фаза
с увеличением дальности погрешность измерения увеличивается. Информация о
дальности извлекается на основе фазового детектора. Однако в таких системах для
обеспечения требуемой точности регистрации дальности или фазовой задержки в условия наличия большого динамического
диапазона изменения необходимы решения по жесткой стабилизации амплитуды
отраженного сигнала особенно на входе аналогового фазового детектора. В цифровом фазовом детекторе фазовая задержка
в большинстве случаев находится по временному сдвигу характерных точек
анализируемых гармонических компонент, например нулей. Однозначный цикл фазовых
измерений составляет 2p. При цифровом детекторе требования по стабилизации амплитуды входного гармонического сигнала несколько сглаживаются.
. Т.е. при заданной относительной погрешности измерения фаза
с увеличением дальности погрешность измерения увеличивается. Информация о
дальности извлекается на основе фазового детектора. Однако в таких системах для
обеспечения требуемой точности регистрации дальности или фазовой задержки в условия наличия большого динамического
диапазона изменения необходимы решения по жесткой стабилизации амплитуды
отраженного сигнала особенно на входе аналогового фазового детектора. В цифровом фазовом детекторе фазовая задержка
в большинстве случаев находится по временному сдвигу характерных точек
анализируемых гармонических компонент, например нулей. Однозначный цикл фазовых
измерений составляет 2p. При цифровом детекторе требования по стабилизации амплитуды входного гармонического сигнала несколько сглаживаются.
В фазовых методах дальнометрии можно кроме
традиционных использовать цифровые методы обработки сигнала, когда излученное и
отраженный сигналы синхронно оцифровываются, заносятся в память, для
отраженного сигнала вводится операция накопления. Начало оцифровки
осуществляется от характерных точек опорного и отраженного гармонических
сигналов (например, нуль) и заканчивается в конце периода отраженного сигнала.
При оцифровке информация по опорному сигналу и принятому заносится в память
раздельно синхронно с моментами поступления импульсов тактовой частоты АЦП.
Операции повторяются с применением накопления Таким образом число тактов
генератора АЦП или число ячеек в памяти между записью нулей есть измеряемая
дальность. Предложенный способ
обработки сигнала представляется одним из вариантов цифровой квазиоптимальной
фильтрацией. Использование же гармонического сигнала при излучении, как будет
показано в примере, до минимума снижает полосу приемного тракта и, соответственно
его чувствительность. Далее существенное снижение чувствительности
осуществляется за счет введения операции цифрового суммирования. При этом
снижение чувствительности пропорционально
корню из числа накапливаемых периодов в выборке. При цифровом фазовом
детектировании дальность до объекта может
находится по числу ячеек соответствующих нулевым точкам гармонических сигналов,
занесенных в память. Погрешность измерения дальности грубо равна одной второй
периода тактовой частоты АЦП. Для стационарных, эргодических шумов, при
аддитивной смеси сигнал-шум и линейности обработки сигнала в точке замеров фазы
просматривается адекватное решение, когда вместо цифрового квантования и
накопления квантованного сигнала вводится операция усреднения замеров (суммированием показаний
цифрового фазового детектора и делением
суммы на число измерений). Отметим, что фазовый детектор, как правило, уже
использует на своем выходе многопериодное усреднение выходного сигнала. Здесь мы имеем место также
со вторичном накоплением (интегрированием) сигнала.
Далее рассмотрим один из методов коррекции
измерения фазы при отклонении амплитуды отраженного сигнала от
стабилизируемого уровня. Сущность извлечения информации о поправке
полученных измерений сводится к следующему: при существенном отклонении
амплитуды отраженного сигнала от порогового уровня отсчета фиксируют временной
интервал полупериодов опорного и отраженных колебаний и по разности этих
временных интервалов, разделенной на двое извлекают поправку к измерениям фазовой задержки цифрового
фазового детектора. При таком способе требования по стабилизации отраженного
сигнала существенно сокращаются.
Важным вопросом лазерной дальнометрии
является обеспечение их помехозащищенности. Это достигается применением вариационно-параметрической
адаптации, увеличением «мертвой зоны» и созданием знакопеременной функции
селекции по дальности. Для аналоговых фазовых детекторов знакопеременная
функция реализуется как естественная дискриминационная характеристика. «Мертвая
зона» формируется за счет введения адаптационного порога отсчета фазовой
характеристики, в области, прилегающей к дальномеру. Положения нуля
знакопеременной функции селекции по дальности выбирается из условия автоматической
компенсации сигнала помехи, максимум амплитуды которой приходится на
прилегающую к дальномеру пространству. Сигнал от объекта, как плоская преграда
будет принимать свой знак в зависимости от расстояния дальномер- объект.
Используя полученные соотношения, оценим основные параметры дальномера.
Пример: Пусть дальность до объекта составляет 0 - 2000м, а абсолютная
погрешность измерений равна DR = 1м
(относительная погрешность 0,05%). Для обеспечения цикла однозначного измерения
указанной дистанции в пределах Dj = 2p = 360° при Rmax =2000м
значение длины волны модуляции должно быть равно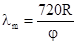 = 4000м. Частота
модуляции при этом равна fm = c/lm = 3108/4000 = 75кГц,
период модулирующего гармонического сигнала равен 1/fm = 13,3310-6с, а
требуемое временное разрешения для цифрового
фазового детектор должно составлять 2DR/с = 6,6 10-9с. Точность измерения фазы в аналоговом фазовом детекторе должна
составлять
= 4000м. Частота
модуляции при этом равна fm = c/lm = 3108/4000 = 75кГц,
период модулирующего гармонического сигнала равен 1/fm = 13,3310-6с, а
требуемое временное разрешения для цифрового
фазового детектор должно составлять 2DR/с = 6,6 10-9с. Точность измерения фазы в аналоговом фазовом детекторе должна
составлять 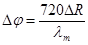 = 0,18°. Поученные требования по
точности отсчетов в цифровом фазовом детекторе 2DR/с = 6,6 10-9с определяет частоту заполнения
измеряемого интервала (150 Мгц), а также
значение погрешности измерения фазы в аналоговом ФД (
= 0,18°. Поученные требования по
точности отсчетов в цифровом фазовом детекторе 2DR/с = 6,6 10-9с определяет частоту заполнения
измеряемого интервала (150 Мгц), а также
значение погрешности измерения фазы в аналоговом ФД (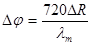 =0,18°). Эти значения находятся в разумных пределах и
легко реализуются при проектировании.
=0,18°). Эти значения находятся в разумных пределах и
легко реализуются при проектировании.
Требования по мощности излучения находятся
по формуле локации
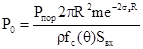 (NH)-1\.2, (9.8)
(NH)-1\.2, (9.8)
где NH = tвыборки/(1/fm)= 75 103 при tвыборки = 1с –
число накапливаемы импульсов (число усреднения измерений);
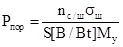 пороговый уровень отсчёта; nс/ш=5 – отношение сигнал/шум; sш - среднеквадратичное
значение суммарного, приведенного ко входу усилителя шума; sш = (st + sdr)1/2; st={Nш[B2/(Гц)]Df }1,2- среднеквадратичное значение теплового шума усилителя; sdr =
пороговый уровень отсчёта; nс/ш=5 – отношение сигнал/шум; sш - среднеквадратичное
значение суммарного, приведенного ко входу усилителя шума; sш = (st + sdr)1/2; st={Nш[B2/(Гц)]Df }1,2- среднеквадратичное значение теплового шума усилителя; sdr =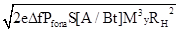 - среднеквадратичное значение дробового
шума германиевого лавинного фотодиода;
- среднеквадратичное значение дробового
шума германиевого лавинного фотодиода;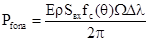 - мощность фоновой
засветки; R = 2000м - дальность до объекта; m = 0,3 – индекс модуляции: r = 0,1 – коэффициент
отражения поверхности объекта;
- мощность фоновой
засветки; R = 2000м - дальность до объекта; m = 0,3 – индекс модуляции: r = 0,1 – коэффициент
отражения поверхности объекта;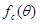 = 0,5 - индикатриса рассеяния;
= 0,5 - индикатриса рассеяния;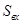 = 2p 10-4м2 -площадь входного окна приемного
объектива; {Nш[В2/Гц]}1/2
= 4нВ/Гц1/2- спектральная плотность теплового шума,
приведенного ко входу усилителя;
= 2p 10-4м2 -площадь входного окна приемного
объектива; {Nш[В2/Гц]}1/2
= 4нВ/Гц1/2- спектральная плотность теплового шума,
приведенного ко входу усилителя; 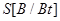 = 300 - вольт-ваттовая характеристика лавинного
фотодетектора;
= 300 - вольт-ваттовая характеристика лавинного
фотодетектора; 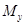 = 100 - коэффициент лавинного
умножения ЛФД; sS = 0,001м-1- коэффициент объемного рассеяния аэрозоля; Df = fm/2Q = 500Гц - полоса приема избирательного
усилителя;Q = 75 - добротность контура; е =
1,6 10-19к - заряд электрона; S[A/Bt] = 0,5 - ампер-ваттовая характеристика
ЛФД; RH = 1кОм - сопротивление нагрузки ЛФД; E[Bt/м2А°] = 0,1 - плотность мощности
солнечного фона у земли в единичной полосе; W = 5 10-3рад - угол поля зрения
приемного объектива; Dl[A°] = 100 –оптическая полоса приема в ангстремах. Для
принятых значений мощность передатчика составляет c учетом накопления принятого сигнала десятки милливатт, без накопления
единицы ватт.
= 100 - коэффициент лавинного
умножения ЛФД; sS = 0,001м-1- коэффициент объемного рассеяния аэрозоля; Df = fm/2Q = 500Гц - полоса приема избирательного
усилителя;Q = 75 - добротность контура; е =
1,6 10-19к - заряд электрона; S[A/Bt] = 0,5 - ампер-ваттовая характеристика
ЛФД; RH = 1кОм - сопротивление нагрузки ЛФД; E[Bt/м2А°] = 0,1 - плотность мощности
солнечного фона у земли в единичной полосе; W = 5 10-3рад - угол поля зрения
приемного объектива; Dl[A°] = 100 –оптическая полоса приема в ангстремах. Для
принятых значений мощность передатчика составляет c учетом накопления принятого сигнала десятки милливатт, без накопления
единицы ватт.
Характер изменения мощности излучения от
величины коэффициента лавинного умножения для приведенных шумов определяется
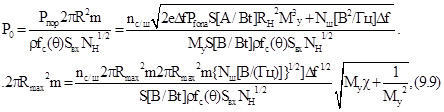
где
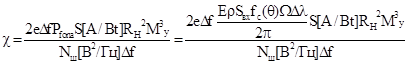 -
-
отношение
дисперсии дробовых шумов лавинного фотодетектора к дисперсии тепловых шумов.
При малой дальности и высокоточных измерениях, т.е. при относительно высокой
частоте модуляции реализовать фазовую высокоточную селекцию целей не представляется
возможным. Поэтому при обработке отраженного сигнала используют принципы гетеродинирования.
9.2.1. Гетеродинирование
Метод гетеродинирования состоит в том, что
за счет введения гетеродина понижают высокую частоту принятого и опорного
сигналов до необходимого низкого уровня с сохранением относительной фазовой
задержки. Здесь относительное изменение фазы на ВЧ и УПЧ по отношению к общему
циклу фазы равному 2p равны, что адекватно равенству отношений времени
задержки принятого ВЧ
сигнала и сигнала полученного при гетеродинировании низкочастотного к
соответствующим периодам. Т.е. происходит как бы растяжка (масштабирование)
времени задержки принятого сигнала t=2R/c. Рассмотрим это явление
при математической интерпретации. Излученный и отраженный сигнал до гетеродинирования
представим
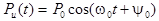 ;
; 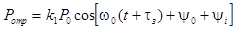 ,
,
где P0 - типовое значение
мощности; 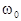 - частота световых коле
- частота световых коле
баний; 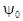 - начальная фаза; k1 - коэффициент, учитывающий
потери сигнала при прохождении его в среде распространения, при отражении от
объекта и т.д.;
- начальная фаза; k1 - коэффициент, учитывающий
потери сигнала при прохождении его в среде распространения, при отражении от
объекта и т.д.; 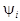 - фазовый сдвиг оптических
колебаний при отражении от объекта;
- фазовый сдвиг оптических
колебаний при отражении от объекта; 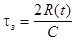 - задержка сигнала, R(t) - текущее значение
дальности до объекта;
- задержка сигнала, R(t) - текущее значение
дальности до объекта; 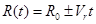 , где R0 - точка схватывания объекта ;
, где R0 - точка схватывания объекта ; 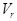 - радиальная скорость сближения
объекта и локатора. Процесс гетеродинирования происходит путем подачи на
смесители сигнала гетеродина
- радиальная скорость сближения
объекта и локатора. Процесс гетеродинирования происходит путем подачи на
смесители сигнала гетеродина
Pg(t) = P0gcos(wg(t)+jg) и сигналов. Запишем результирующие сигналы после смесителей при введении фильтрации
разностных частот:
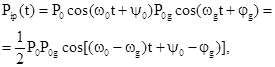
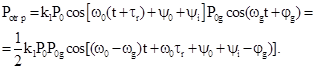
Т.е. на
промежуточной частоте (период- Tp), в
процессе гетеродинирования происходит расширение временного интервала задержки
от tr
до Dtp , т.е. происходит масштабирование (растяжка) фиксируемого
интервала tr по ВЧ колебания при сохранении
условия равенства фазовых соотношений w0t r= wpDtp. Действительно, если по условию процесса
гетеродинирования (условие подобия двух треугольников) написать пропорцию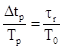 . Отсюда
. Отсюда 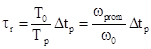 , или
, или 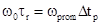 . Что
подтверждает выше изложенное. Процесс фазового детектирования для малого уровня
сигналов является квазиоптимальной операцией (корреляционной) обработки
принимаемого сигнала относительно опорного. Поэтому результирующий сигнал – Up рассмотрим как произведение
отраженного и опорного сигналов. Далее используя фильтрацию ограничимся
разностной частотой
. Что
подтверждает выше изложенное. Процесс фазового детектирования для малого уровня
сигналов является квазиоптимальной операцией (корреляционной) обработки
принимаемого сигнала относительно опорного. Поэтому результирующий сигнал – Up рассмотрим как произведение
отраженного и опорного сигналов. Далее используя фильтрацию ограничимся
разностной частотой

После усреднения (математически
операция - интегрирование выражения) в пределах периода промежуточной частоты
или принимаемого сигнала, т.е. убирая высокочастотную компоненту фазы-Yi получим
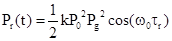 ; или
; или
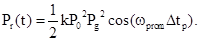
При регистрации относительно больших дальностей
с малой погрешностью возникает проблема однозначного отсчета измеряемой
дальности. Рассмотрим пределы однозначного отсчета дальности. Условие
однозначного отсчета при цифровом фазовом детекторе равно 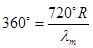 или lm=2Rmax.
Погрешность измерений оценивается по формуле
или lm=2Rmax.
Погрешность измерений оценивается по формуле 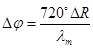 .
.
Подставляя в неё lm=2Rmax,
имеем 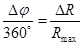 , т.е. чем меньше DR и больше Rmax, тем меньше погрешность измерения фазы Dj. Очевидно, есть аппаратурные ограничения по минимуму
регистрации фазового цикла, например, шумы, при которых и оцениваются
предельные параметры системы-Djpred. Структурная
схема такого фазового дальномера приведена на рис. 9.10 Нормальное функционирование
фазового детектора предъявляет жесткие требования к постоянству уровня
напряжения на выходе УПЧ. Решение указанных задач в условиях значительного
изменения уровня входных сигналов достигается введением в приемный тракт
инерционной АРУ. В качестве регулируемых каскадов используется первые каскады
УПЧ. Однако для малоинерционных систем такое решение является не приемлемым,
особенно при большом динамическом
диапазоне изменения входного сигнала (по мощности 40-130 db). Поэтому в быстродействующие системы фазовой
дальнометрии вводят нелинейные ограничители амплитуды с соответствующей
частотной фильтрацией. При введении любого вида ограничителей, также как и
применение логарифмического усилителя приводит к появлению нелинейных искажений
и к расширению спектра принятого сигнала, что в конечном итоге существенно
повышает погрешность измерений. Поэтому такие усилители снабжаются узкополосными
избирательными фильтрами. Необходимо помнить, что постоянная времени
инерционности контура и, соответственно, время становления системы зависят от
его полосы примерно как tк=(2Df)-f=f0/qd, где qd-добротность контура.
, т.е. чем меньше DR и больше Rmax, тем меньше погрешность измерения фазы Dj. Очевидно, есть аппаратурные ограничения по минимуму
регистрации фазового цикла, например, шумы, при которых и оцениваются
предельные параметры системы-Djpred. Структурная
схема такого фазового дальномера приведена на рис. 9.10 Нормальное функционирование
фазового детектора предъявляет жесткие требования к постоянству уровня
напряжения на выходе УПЧ. Решение указанных задач в условиях значительного
изменения уровня входных сигналов достигается введением в приемный тракт
инерционной АРУ. В качестве регулируемых каскадов используется первые каскады
УПЧ. Однако для малоинерционных систем такое решение является не приемлемым,
особенно при большом динамическом
диапазоне изменения входного сигнала (по мощности 40-130 db). Поэтому в быстродействующие системы фазовой
дальнометрии вводят нелинейные ограничители амплитуды с соответствующей
частотной фильтрацией. При введении любого вида ограничителей, также как и
применение логарифмического усилителя приводит к появлению нелинейных искажений
и к расширению спектра принятого сигнала, что в конечном итоге существенно
повышает погрешность измерений. Поэтому такие усилители снабжаются узкополосными
избирательными фильтрами. Необходимо помнить, что постоянная времени
инерционности контура и, соответственно, время становления системы зависят от
его полосы примерно как tк=(2Df)-f=f0/qd, где qd-добротность контура.
Пример: Рассмотрим выбор параметров лазерной
рулетки, обеспечивающей измерение дистанции 0-20м с погрешностью DR=1мм (относительная погрешности
измерений 0,005%). За основу возьмем цифровой фазовый детектор, в котором цикл
однозначного отсчета находится в пределах 2p, в диапазоне lm=Rодн=20м. Частота модуляции при
этом равна fm=c/lm=15 106Гц.
Очевидно, что для обеспечения указанной погрешности измерений частота fm является высокой (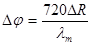 =36 10-3). Поэтому необходимо использовать принцип
гетеродинирования, т.е. перейти на промежуточную частоту, значение
которой определим исходя из требования допустимой стабильности
гетеродина. Исходя из требования простоты схемотехнической реализации
нестабильность гетеродина должна быть не хуже
fпром/
fm» 10-3, что легко реализуется при
использовании LC элементов и комплектующих цифровой техники. Т.е.
промежуточная частота должна быть порядка 15 кГц. В противном случае для
снижения требований по нестабильности гетеродина надо повышать значение
промежуточной частоты. Масштабный коэффициент расширения временного интервала
измерений находится fm / fпром = Тпром/Тm » 103.Время
задержки отраженного сигнала по отношению к опорному tз=2Rодн/с = 132нс, а по промежуточной
частоте найдем из основополагающего соотношения fпромDt = fmtз, откуда Dt = fmtз/ fпром = 132 10-6с = 132мкс. Если измерять
дальность в одночастотном варианте модуляции, то для цифрового фазового
детектора надо мерить фазу на низкой промежуточной частоте с точностью не хуже
360°/(Rодн/DR) = 18 10-3градуса.
Во временном же представлении, период частоты заполнения временного интервала
адекватного погрешности задержки отраженного сигнала на промежуточной частоте
равен Dt/(Rодн/DR) = 6,6 нс, т.е. частота
заполнения и подсчета в цифровом ФД составляет порядка 150 МГц. При использовании
цифрового детектора такие цифры дают надежды на реализуемость такой системы.
=36 10-3). Поэтому необходимо использовать принцип
гетеродинирования, т.е. перейти на промежуточную частоту, значение
которой определим исходя из требования допустимой стабильности
гетеродина. Исходя из требования простоты схемотехнической реализации
нестабильность гетеродина должна быть не хуже
fпром/
fm» 10-3, что легко реализуется при
использовании LC элементов и комплектующих цифровой техники. Т.е.
промежуточная частота должна быть порядка 15 кГц. В противном случае для
снижения требований по нестабильности гетеродина надо повышать значение
промежуточной частоты. Масштабный коэффициент расширения временного интервала
измерений находится fm / fпром = Тпром/Тm » 103.Время
задержки отраженного сигнала по отношению к опорному tз=2Rодн/с = 132нс, а по промежуточной
частоте найдем из основополагающего соотношения fпромDt = fmtз, откуда Dt = fmtз/ fпром = 132 10-6с = 132мкс. Если измерять
дальность в одночастотном варианте модуляции, то для цифрового фазового
детектора надо мерить фазу на низкой промежуточной частоте с точностью не хуже
360°/(Rодн/DR) = 18 10-3градуса.
Во временном же представлении, период частоты заполнения временного интервала
адекватного погрешности задержки отраженного сигнала на промежуточной частоте
равен Dt/(Rодн/DR) = 6,6 нс, т.е. частота
заполнения и подсчета в цифровом ФД составляет порядка 150 МГц. При использовании
цифрового детектора такие цифры дают надежды на реализуемость такой системы.
9.2.2. Последовательная
высокоточная оценка дистанции до объекта при многочастотной модуляции излучения
Характеристика фазового детектора в
простейшем представлении имеет вид периодической функции F(j) = cosj. Однозначный цикл измерений составляет jодн = p¸2p, т.е. во вне пределах этого цикла форма фазовой характеристики
повторяется, что приводит к неоднозначному отсчету дальности. Неоднозначность
измерений устраняется за счет введения последовательной многочастотной модуляции
в простейшем случае двухчастотной. При такой последовательной оценки дистанции
на низкой частоте модуляции, когда дальность в режиме однозначного отсчета
определяется грубо с определенной погрешностью отсчета. При высокой частой
модуляции фиксируется с высокой точностью часть дистанции, определяемая
погрешностью измерений при низкой частоте модуляции. В этом случае длина волны
высокой частоты модуляции должна быть равна погрешности грубого измерения
дистанции. Характер изменения фазовых характеристик для ВЧ и НЧ сигнала
модуляции показано на рис.9.11, где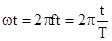 . Отмеченный маркером интервал соответствует погрешности
измерения дистанции при низкой частоте модуляции-Rодн и
должен быть равен длине волны модулирующего сигнала НЧ. Измеренная с
высокой точностью дистанция при этом равна
. Отмеченный маркером интервал соответствует погрешности
измерения дистанции при низкой частоте модуляции-Rодн и
должен быть равен длине волны модулирующего сигнала НЧ. Измеренная с
высокой точностью дистанция при этом равна
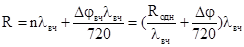 (9.11)
(9.11)
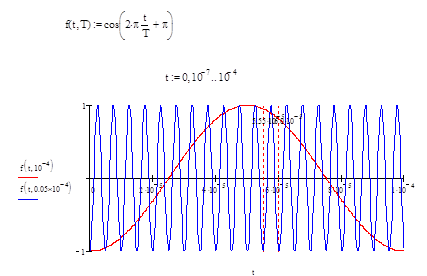
9.11.
Характер изменения фазовых характеристик для
ВЧ и НЧ сигнала модуляции
Пример: Требуется определить параметры дальномер для заполнения кадастра с
параметрами R=0¸5 км с погрешностью 5см (относительная
погрешность 0,001%). Дальномер работает по уголковому отражателю.
1. Из условия однозначного отсчета
дальности найдем длину волны
низкочастотной модуляции 2Rma = lнч= 10км или fm1 = C/l=
30кГц. С целью упрощения системы полученную частоту fm1=C/l=30кГц
принимаем за промежуточную.
2.Исходя из реально реализуемой погрешности измерения
фазы найдем погрешность измерения дистанции при низкочастотной модуляции. Если
за основу погрешности цифрового детектора принять типовую на сегодняшний день
частоту АЦП порядка 10 нс, то погрешность измерений за счет оцифровки
составляет ±5нс и такую же пусть составит систематическая
ошибка, связанная с изменениями совокупности дестабилизирующих факторов
(амплитуда на входе, порог отсчета, изменение температуры окружающей среды и т.
д.). Тогда 2DR/c=20нс или абсолютная погрешность
составит DR1=12м.
3.На основании этой цифры найдем
длину волны высокоточной модуляции 2DR1=lm2=24м или fm2=c/lm2=12,5 мГц.
4.Требования по измерению фазы при lm2 составит
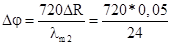 =1,5°.
=1,5°.
Измерение дальности с
такой погрешностью на такой высокой частоте
является затруднительной задачей. Поэтому мы вынуждены переходить на промежуточную частоту, которая согласно п.1 равна 30
кГц. Требования к погрешности измерения задержки по периоду промежуточной частоты
найдем их из известного выражения wпрDt= wвчDtз или wпрDt = 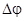 . Тогда D t=
. Тогда D t= 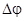 (рад)/2pfпр = 15мкс,
где fпр= с/am1. Видно,
что мы имеем существенный дополнительный запас как по увеличению дальности, так
и по снижению погрешности измерений. Структурная схема такого дальномера
представлена на рис.9.12. К отличительной особенности анализируемой структурной схемы следует
отнести использование ЛФД в режиме смесителя .
(рад)/2pfпр = 15мкс,
где fпр= с/am1. Видно,
что мы имеем существенный дополнительный запас как по увеличению дальности, так
и по снижению погрешности измерений. Структурная схема такого дальномера
представлена на рис.9.12. К отличительной особенности анализируемой структурной схемы следует
отнести использование ЛФД в режиме смесителя .
9.2.3. Измерение дальности
по фазовому портрету
принятого сигнала
Пусть на вход приемника поступает сигнал от
объекта, модулирующую функцию которого
общем виде можно представить

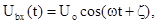
где
V -
фазовый сдвиг обусловленный переотражением от рельефа. Представляя 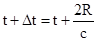 , где R -
расстояние до объекта, отсюда
, где R -
расстояние до объекта, отсюда
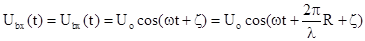 ,
,
где
l -длина волны модулирующего
гармонического сигнала. Если нет опорного сигнала, информацию о дальности можно
извлечь при установке дополнительного приемника, расположенного на расстоянии d
от основного вдоль линии распространения излучения, колебания которого можно
представить
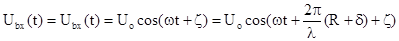 .
.
При
фазовом детектировании этих колебаний
получим лишь информацию о приращении d.
Вместо двух антенн можно использовать линию задержки, соединенной со вторым
входом схемы отношений. Рассмотрим отношение этих колебаний
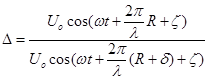 .
(9.12)
.
(9.12)
Результаты
расчета приведены на рисунках 9.13, 9.14. Информация о рельефе появляется в
определенный момент времени в виде треугольного импульса. Отношение не меняется
для малых приращений рельефа, связанных с V
.
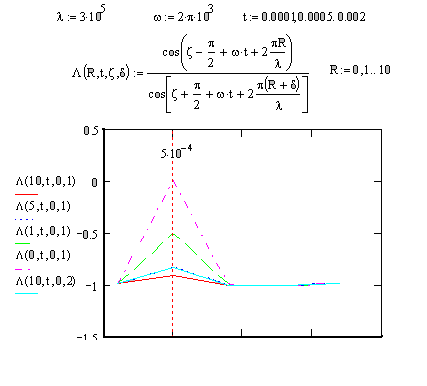
Рис. 9.13. Поведение функции селекции объекта
на определенной дальности
Чем
больше разнос антенн или больше задержка, то тем ближе искомое отношение
приближается к линейной зависимости в функции от дальности до объекта-R, но
динамически диапазон изменения отношения при этом несколько уменьшается. Таким
образом, используя задержку в схеме отношений можно измерять расстояние до
пассивного источника.
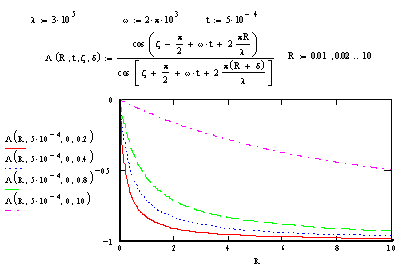
Рис.
9.14. Характер изменения отношения во времени в
зависимости
от дальности до объекта
9.3. Принципы помехозащиты
фазовых
систем ближней дальнометрии
Помехозащищенность систем дальнометрии с фазовой
модуляцией при малом значении Rmax (системы
ближней дальнометрии) в рассмотренных вариантах достигается:
· За счет создания в пределах одного фазового
цикла знакопеременной функции селекции по дальности, под которой понимается
характер изменения регистрируемого параметра от дальности до объекта. При этом
помеховый сигнал как протяженный объект, приходящий от участков всей дистанции
компенсируется, а от объекта повторяет её форму. При этом начальный фазовый сдвиг определяется из условия обеспечения
минимума аэрозольной помехи:
· Использования фазоимпульсных методов
регистрации объектов.
· Введения вариационно-параметрической адаптации в фазо-адаптивных методах
дальнометрии.
Пример1: Пусть дальность до объекта
составляет 15 и 5м в зависимости от типа решаемой задачи, а абсолютная
погрешность измерений равна DR = ±1м. Для обеспечения цикла
однозначного измерения указанной дистанции в пределах Dj = 2p= 360° при Rоднознач=20м
значение длины волны модуляции должно быть равно 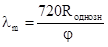 =40м. Частота модуляции при этом равна
fm= c/lm== 3×108/40=7,5МГц, Точность измерения фазы в
аналоговом фазовом детекторе должна составлять
=40м. Частота модуляции при этом равна
fm= c/lm== 3×108/40=7,5МГц, Точность измерения фазы в
аналоговом фазовом детекторе должна составлять 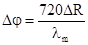 =18°. В свою очередь точность временного отсчета этого
фазового набега в цифровом детекторе при погрешности 1м составляет 6,6 нс.
=18°. В свою очередь точность временного отсчета этого
фазового набега в цифровом детекторе при погрешности 1м составляет 6,6 нс.
Фазовая система дальнометрии
железнодорожного транспорта должна для обеспечения помехоустойчивости
формировать знакопеременную функцию селекции по дальности и ориентировочно
иметь следующий вид
Рис.9.15.
Функция селекции по дальности фазового дальномера
Объект фиксируется по отрицательному
напряжению (по отрицательному периоду) в пределах 6-16м в зависимости от выбора схемы обработки (н.п.-порог+знак
производной по напряжению и др.). Весовые коэффициенты по знаку напряжения
подбираются таким образом, чтобы в однородной аэрозольной помехи с учетом
закона распределения обратного рассеяния помеховый сигнал бы компенсировался.
При подходе к кромке облачности должен преобладать сигнал положительной
полярности (отличный по знаку от полезного). Логика работы фазовой системы
дальнометрии сводится к следующей последовательности:
1.Фазовым
методом фиксируют с заданной погрешностью первую заданную высоту Н1=15м;
2.Этим же методом фиксируют любую
ближайшую высоту, отстоящую от 15м, например Н2 =14м и время между
этими отсчетами Dt;
Далее определяют скорость
снижения носителя
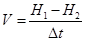 ;
;
С помощью микроконтроллера по
необходимости фиксируем вторую Н3 высоту, используя например
алгоритм 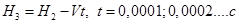 . Поэтому в этих пределах изменения
дистанции динамический диапазон изменения сигнала составляет
. Поэтому в этих пределах изменения
дистанции динамический диапазон изменения сигнала составляет
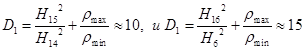 .
.
В
настоящее время существуют операционные логарифмические усилители с
демодулятором с динамически диапазоном 40-80 дб,
|
Микро
схема
|
Рабочая частота, макс.
|
Динамич
диапазон, дБ
|
Соответствие логарифмй характеристике, дБ
|
Фазовая погрешность, град.
|
Время отклика, нс
|
Потребляя
мощность,
мВт
|
|
AD606
|
50 МГц
|
80
|
±0.4
|
±3
|
400
|
65
|
|
|
|
|
|
|
|
|
Требования по мощности излучения находятся по
формуле локации
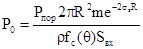 ,
,
где
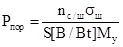 ¾
¾
пороговый уровень отсчёта; nс/ш = 3 –
отношение сигнал/шум; sш - среднеквадратичное значение
суммарного, приведенного ко входу усилителя шума; sш = (st + sdr)1/2; st = {[Nш[нв/(ÖГц)]2]Df }1/2- среднеквадратичное значение теплового шума усилителя; sdr =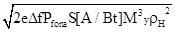 - среднеквадратичное значение дробового
шума лавинного фотодиода;
- среднеквадратичное значение дробового
шума лавинного фотодиода;
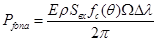 -
-
мощность фоновой засветки; R = 20м - дальность до объекта; m=0,7 – индекс использования первой гармоники
в процессе преобразования лазер-фотодиод; r = 0,1 – коэффициент отражения
поверхности объекта;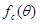 = 0,5 - индикатриса рассеяния;
= 0,5 - индикатриса рассеяния;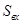 = p 2,2510-4м2-площадь
входного окна приемного объектива; {Nш[В2/Гц]}1/2
= 4нВ/Гц1/2 - спектральная плотность теплового
шума, приведенного ко входу логарифмического усилителя с демодулятором;
= p 2,2510-4м2-площадь
входного окна приемного объектива; {Nш[В2/Гц]}1/2
= 4нВ/Гц1/2 - спектральная плотность теплового
шума, приведенного ко входу логарифмического усилителя с демодулятором; 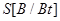 =300 - вольт-ваттовая характеристика
лавинного фотодетектора;
=300 - вольт-ваттовая характеристика
лавинного фотодетектора; 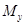 = 100 - коэффициент лавинного умножения
ЛФД; sS = 0,1-1м-1- коэффициент объемного рассеяния
аэрозольной помехи; Df = fm/2Q = 75000Гц- полоса приема избирательного усилителя; Q= 100 - добротность контура; е =1,6 10-19к - заряд электрона; S[A/Bt] =0,5 - ампер-ваттовая характеристика
ЛФД; rH = 100кОм = 105 - характеристическое
сопротивление нагрузки ЛФД в виде последовательного контура; E[Bt/м2А°] = 0,1
плотность мощности солнечного фона у земли в единичной полосе; W = 1 10-3рад - угол поля зрения
приемного объектива; Dl[A°] = 500 – оптическая полоса приема в ангстремах.
Характер изменения мощности излучения от величины коэффициента лавинного умножения
для приведенных шумов определяется
= 100 - коэффициент лавинного умножения
ЛФД; sS = 0,1-1м-1- коэффициент объемного рассеяния
аэрозольной помехи; Df = fm/2Q = 75000Гц- полоса приема избирательного усилителя; Q= 100 - добротность контура; е =1,6 10-19к - заряд электрона; S[A/Bt] =0,5 - ампер-ваттовая характеристика
ЛФД; rH = 100кОм = 105 - характеристическое
сопротивление нагрузки ЛФД в виде последовательного контура; E[Bt/м2А°] = 0,1
плотность мощности солнечного фона у земли в единичной полосе; W = 1 10-3рад - угол поля зрения
приемного объектива; Dl[A°] = 500 – оптическая полоса приема в ангстремах.
Характер изменения мощности излучения от величины коэффициента лавинного умножения
для приведенных шумов определяется
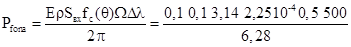 =3 10-4Вт,
=3 10-4Вт,
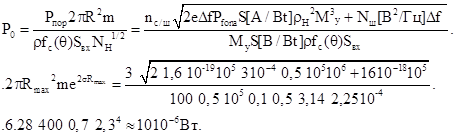
При малой дальности и высокоточных
измерениях, т.е. при относительно высокой частоте модуляции реализовать фазовую
высокоточную селекцию целей не всегда представляется возможным. Поэтому при
обработке отраженного сигнала используют принципы гетеродинирования. Весовые
коэффициенты по знаку напряжения подбираются таким образом, чтобы в однородной
аэрозольной помехи с учетом закона распределения обратного рассеяния помеховый
сигнал бы компенсировался. При подходе к кромке облачности должен преобладать
сигнал положительной полярности (отличный по знаку от полезного).
9.4. Двухчастотный метод селекции
объектов
Использования двух частотного в дальнометрии железнодорожного транспорта
связано с вопросами устранения неоднозначности
дистанции при высоких требованиях по точности измерения дистанции до объекта.
Напомним, что ранее для решения этой проблемы использовали принцип
гетеродинирования или последовательную двухчастотную модуляцию светового
излучения, когда однозначное, грубое измерение дальности проводится на низкой
частоте модуляции, а высокоточное измерение проводится на высокой частоте, период
или длина волны модуляции которой сравнимы а с погрешностью измерения дистанции
при низкочастотной модуляции. Этот же эффект можно получить при
одновременном излучении двух частот. Но при этом увеличивается быстродействие
системы и существует возможность распознавания образа лоцируемого объекта.
9.4.1. Принцип работы двухчастотного метода
измерения дистанции
Для начала
рассмотрим двухчастотный метод измерения дальности до объекта. Пусть излучаются
два оптических сигнала:
í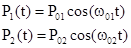 .
.
Соответственно, отраженный сигнал на входе фотодетектора
имеет вид :
í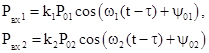 .
.
Возьмем за основу принцип когерентного сложения амплитуд отраженного
сигнала. Предположим, что большая часть падающего квазимонохроматического
когерентного излучения двух волн не дифрагирует, а волны достигшие плоскости Н чувствительного слоя
фотодетектора, можно представить в комплексном виде
í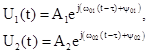 , где
, где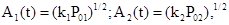
Тогда возмущенное поле в Н задается выражением
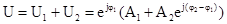 ,
,
и интенсивность, зарегистрированная
чувствительным слоем фотоприемника, помещенного в плоскости Н, определяется по
формуле
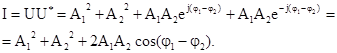
Здесь результирующая фаза
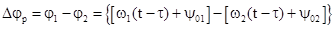
есть фазовый сдвиг между
составляющими. Т.е. на выходе фотодетектора имеем две компоненты отображающие
постоянные составляющие и составляющую, зависящую от фазовых сдвигов двух
входных сигналов.
Найдём значение 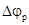 :
:
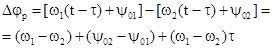 ,
,
где, принимая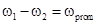 ,
, 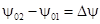 -
разность фаз ВЧ сигнала, получим:
-
разность фаз ВЧ сигнала, получим: 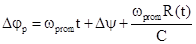
или
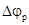 =
=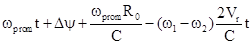
Так как
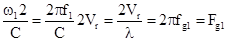 , а
, а 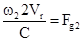 .
.
Таким образом, результирующий сигнал на выходе
фотодетектора равен
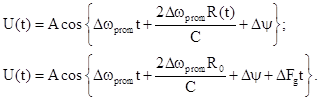
Т.е. фаза на промежуточной
частоте пропорциональна дальности до цели
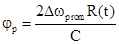 .
.
Для извлечения
информации по дальности как уже было отмечено необходимо ввести фазовый
детектор, фаза которого на промежуточной частоте будет определяться уже
рассмотренным выше выражением.
При измерении дальности в условиях однозначного отсчета дальности
значение 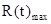 и
и 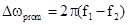 связаны соотношением
связаны соотношением
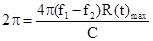 ,
,
отсюда 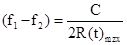 ,
,
т.е. разность частот обратно пропорциональна
максимальной дистанции измерения. Так
при 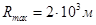 разность частот должна
быть равна, а при
разность частот должна
быть равна, а при 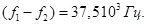 Здесь с повышением
Здесь с повышением 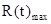 для обеспечения
однозначного отсчета надо уменьшать диапазон отстройки лазеров
для обеспечения
однозначного отсчета надо уменьшать диапазон отстройки лазеров 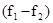 или обеспечить соответствующий
разнос частот модуляции.
или обеспечить соответствующий
разнос частот модуляции.
Точность
определения фазы найдем как
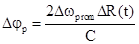 [рад] или
[рад] или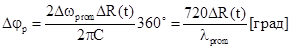
и при DR(t)=1м значение Dj = 0,1°. Такие точности погрешности измерений 0,1/360 при низкой разностной
частоте проще реализуются с применением цифровых детекторов 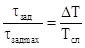 или временное разрешение DТ
относительно периода промежуточной частоты
или временное разрешение DТ
относительно периода промежуточной частоты 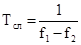 равно
равно 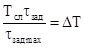 ,
где
,
где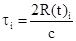 .
Для разрешения по дальности tзад = Dtmin »
10нс и tзадmax =
2R(t)max/c = 4000/3 108=
13,3 мкс , для периода
.
Для разрешения по дальности tзад = Dtmin »
10нс и tзадmax =
2R(t)max/c = 4000/3 108=
13,3 мкс , для периода
Тсл=1/(f1-f2)=(75 103)-1=
0,013333 103c значение DТ = tзад
= 10нск,
что не входит в противоречие с условием обеспечения малой погрешности
измерения дальности.
Погрешность измерения дистанции определяется
относительной стабильностью разности частот излучения f1 и f2: 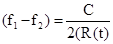 или, т.е
или, т.е
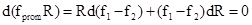 или
или 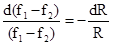 .
.
При погрешности
измерения
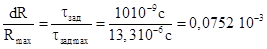
стабильность разности частот излучения должна иметь тот же
порядок. Для двух идентичных лазеров это не высокая стабильность даже при
изменении окружающей температуры в широких пределах. Однако для упрощения
технического решения можно отказаться от одного лазера, а второй источник
излучения можно организовать за счет введения доплеровского смещения в основном
источнике излучения, например за счет формирования излучения от вращающего
тела, приводимого микродвигателем
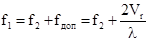 .
.
При l = 0,8 мкм и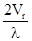 = 75 кГц радиальная скорость тела вращения Vr
= 0,3
м/с. Радиальная скорость тела вращения равна произведению угловой скорости на
радиус вращающего тела r. Тогда угловая скорость или число оборотов двигателя
для выбранных параметров должно быть равно W =
= 75 кГц радиальная скорость тела вращения Vr
= 0,3
м/с. Радиальная скорость тела вращения равна произведению угловой скорости на
радиус вращающего тела r. Тогда угловая скорость или число оборотов двигателя
для выбранных параметров должно быть равно W = 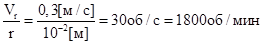 . Естественно при такой модели
построения системы возникает вопрос о влиянии доплеровского смешения уже при
отражении от объекта и ширине
спектра смещенной синтезированной линии излучения.
. Естественно при такой модели
построения системы возникает вопрос о влиянии доплеровского смешения уже при
отражении от объекта и ширине
спектра смещенной синтезированной линии излучения.
Доплеровские
компоненты при отражении определяются двумя линиями лазерного излучения (f1 и f2) и разностной доплеровской
частотой
Fg=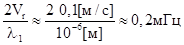 .
.
Аналогичная цифра находится и для второй длины волны.
Рассмотрим влияние скорости объекта при условии установки на выходе
фотодетектора смесителя и адаптивного
фильтра, настроенного на переменную составляющую разности доплеровских компонент
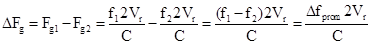 .
.
При 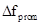 = 75 кГц и Vr=0,5 м/с значение DFg=25 10-5Гц. Из-за большого индекса модуляции
доплеровского сигнала на промежуточной частоте и очень низкой частоты, которая
легко отфильтровывается разделительными цепями приемного тракта, влиянием доплеровской
компоненты разностной частоты можно пренебречь.
= 75 кГц и Vr=0,5 м/с значение DFg=25 10-5Гц. Из-за большого индекса модуляции
доплеровского сигнала на промежуточной частоте и очень низкой частоты, которая
легко отфильтровывается разделительными цепями приемного тракта, влиянием доплеровской
компоненты разностной частоты можно пренебречь.
9.4.2. Измерение дистанции с введением
переброса
фазы опорного сигнала на 180°
В ранее
рассмотренных фазовых методах дальнометрии существенную роль на точность измерения дистанции играет точность установки амплитуды
отраженного сигнала на входе фазового детектора. Сокращение требований к
разбросу амплитуд отраженного сигнала дает метод относительного измерения фазы.
Фаза опорного гармонического сигнала скачком в такт с определенной частотой
изменяется на 180°, а измерение дальности проводится
на выходе фазового линейного детектора как отношение рядом стоящих поочередно
изменяющихся амплитуд в кодовой последовательности в два тактах поочередно
изменяющейся амплитуды.
Для наглядности в качестве физической модели
обработки сигнала в фотоприемном тракте возьмем модель двухчастотного одновременного
излучения, когда два отраженных сигнала подаются на вход фотодетектора, на его
выходе отфильтровываем разностную (промежуточную) частоту с сохранением
присущей для неё фазовой задержкой, усиливаем
и далее подаем её на фазовый детектор, а на второй вход которого
поступает опорный сигнал разностной частоты, фаза которого изменяется скачком
на jс
= 180°. Можно представить другие
модели, но остановимся на отмеченной. Характерная особенность такой модели
такова, что фазовые изменения ВЧ сигнала усредняются и отфильтровываются на
низкочастотной нагрузке фотодетектора. Поэтому и их значениями на выходе
фотодетектора пренебрегаем. В
соответствии с принятыми ограничениями отраженный сигнал на выходе
фотодетектора представим в комплексном
виде
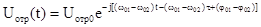 .
.
Если
в опорном сигнале проводить переброс фаза на 180о(процедура,
определяемая функцией jn=(p/2)(-1)k, где k=1,2,3), то опорный сигнал можно
представить в виде непрерывного сигнала, фаза которого изменяется на p с выбранным тактом
частоты переброса, т.е. представляет кодовую последовательность рядом стоящих
импульсов промежуточной частоты длительностью-Тi, фаза в которых относительно
друг друга перебрасывается на p
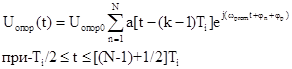 ,
,
где
k-
номер импульса длительностью длительностью Ti кодовой последовательности
сигнала промежуточной частоты; jp=j01-j02;
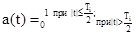 -нормированное значение амплитуды ; Ti
-
протяженность, соответствующая периоду переброса фазы опорного колебания
(длительность импульса в цикле кодовой последовательности); N = 2¸¥
-
число перебросов фазы в принятой выборке;
-нормированное значение амплитуды ; Ti
-
протяженность, соответствующая периоду переброса фазы опорного колебания
(длительность импульса в цикле кодовой последовательности); N = 2¸¥
-
число перебросов фазы в принятой выборке; 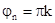 , где k
= 0;1, т.е. jn = o;p или
, где k
= 0;1, т.е. jn = o;p или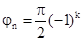 . Введем обозначение
. Введем обозначение 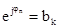 ; bk=+1;-1
при jn=0;p; тогда
; bk=+1;-1
при jn=0;p; тогда
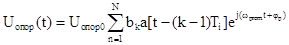 ,
,
то в соответствии с раннее
полученными соотношениями
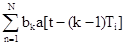 =±1.
=±1.
Если отраженный и опорный сигналы подать на
аналоговый фазовый детектор или на смеситель, то
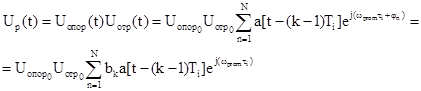 ,
,
где
 , R(t)-текущая дальность до цели.
, R(t)-текущая дальность до цели.
Рассмотрим квадратурную составляющую
результирующего сигнала
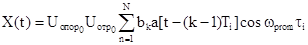
при-Ti/2£t£[(N-1)+1/2]TI
X(t)=0 при t<Ti/2; t>[(N-1)+1/2].
Т.к.
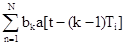 =±1 , то эта
квадратурная составляющая представляет
меандр с изменяющейся амплитудой по дальности. Если в системе обеспечивается
стабилизация амплитуды входного сигнала и её значение в априори известно, то
нормированное значение амплитуды Х(t)
в течение одного импульса пропорционально cos wpromti, отсюда
=±1 , то эта
квадратурная составляющая представляет
меандр с изменяющейся амплитудой по дальности. Если в системе обеспечивается
стабилизация амплитуды входного сигнала и её значение в априори известно, то
нормированное значение амплитуды Х(t)
в течение одного импульса пропорционально cos wpromti, отсюда
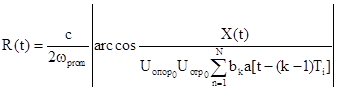 .
.
Преимущество
такого метода состоит в том, что результирующий сигнал в виде меандра можно
усилить узкополосным фильтром, настроенного на первую гармонику, до
необходимого уровня, тем самым повысив отношение сигнал-шум. Во вторых, если
выборка имеет относительное большое число периодов меандра N, то возможно накопление сигнала
Х(t),
что также повышает отношение сигнал-шум в 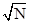 . И в третьих можно вводить переброс фаз не по
закону меандра, а импульсами с более меньшей скважностью что в сочетании с
накоплением эта операция также дает определенный выигрыш в отношении
сигнал-шум.
. И в третьих можно вводить переброс фаз не по
закону меандра, а импульсами с более меньшей скважностью что в сочетании с
накоплением эта операция также дает определенный выигрыш в отношении
сигнал-шум.
Квадратурную
составляющую на базе исходного выражения
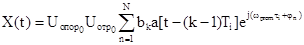
представим
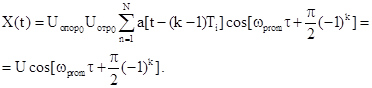
Характер
изменения отраженного сигнала по дистанции определяет функцию селекции по
дальности и для заданного R
представляет отрезок гармонического колебания в интервале одного периода, если
промежуточная частота выбрана из условия однозначного отсчета -рис.9.16
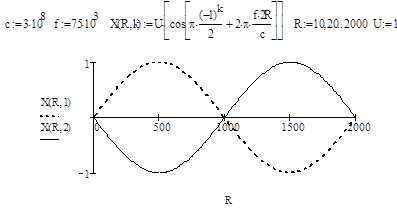
Рис.9.16.
Дистанционная характеристика при различных
значениях ---k=1, _k=2
Для фиксируемого расстояния на выходе ФД как
и отмечено раннее имеет место последовательность импульсов в виде меандра c амплитудой, в зависимости от
дистанции до цели в соответствии с рис.9.17. Частота меандра или частота
переброса определяется условиями обработки результирующего сигнала.

Рис.9.17. Форма
результирующего сигнала на выходе ФД
для
заданной фиксированной дальности R
Рассмотрим
рядом стоящую пару импульсов для k=1,2
и определим разность амплитуд между ними
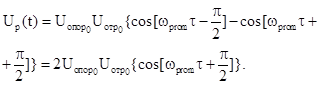
Т.е.
амплитуды в паре имеют разную полярность, но одинаковую амплитуду. Разница этих
амплитуд
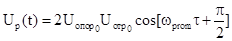 .
.
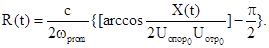 .
.
В процессе перехода на относительно низкую промежуточную частоту
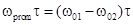 соблюдается
принцип гетеродинирования, когда фазы
соблюдается
принцип гетеродинирования, когда фазы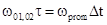 , где
, где 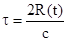 - фазовая задержка отраженного
сигнала по ВЧ сигналу, Dt – задержка на промежуточной
частоте. Выражение
- фазовая задержка отраженного
сигнала по ВЧ сигналу, Dt – задержка на промежуточной
частоте. Выражение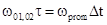 можно
преобразовать
можно
преобразовать 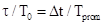 , где T0, Tprom-периоды ВЧ сигнала и
промежуточной частоты. Отсюда фазовая задержка сигнала на промежуточной частоте
равна
, где T0, Tprom-периоды ВЧ сигнала и
промежуточной частоты. Отсюда фазовая задержка сигнала на промежуточной частоте
равна 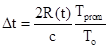 . Т.е. происходит масштабирование (увеличение
значения) отсчитываемого времени, приходящегося на задержку ВЧ сигнала
. Т.е. происходит масштабирование (увеличение
значения) отсчитываемого времени, приходящегося на задержку ВЧ сигнала 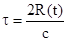 .
.
Если кодовую информацию об амплитуде двух
рядом стоящих результирующих сигналов представить в виде алгоритма
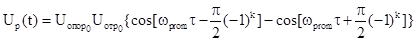 ,
,
где
k
принимает значение 1,2 с определенной частотой переброса фаз, то абсолютное
значение отношения рядом стоящих амплитуд в зависимости от дальности до объекта
имеет вид в соответствующий рис.9.18. Таким образом характер изменения отношения абсалютных значений
амплитуд результирующих сигналов по дистанции
представляет v-образную
функцию селекции по дальности. Указанный
алгоритм работы и вид функции
селекции по дальности, представленный на рис. 9.18можно получить на фазовом
детекторе-модуляторе, когда прием сигнала осуществляется ФЭУ, а опорный сигнал
с изменяющейся фазой подается на его управляющую
сетку.
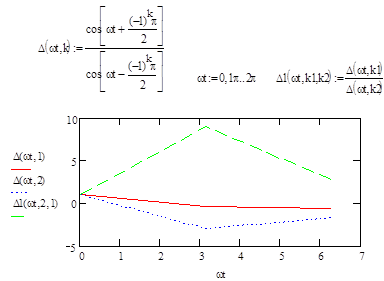
Рис.9.18.
Функция селекции по дальности, сформированная по отношению рядом стоящих
амплитуд в случая переброса фаз по алгоритму
В
качестве фазового индикатора возьмем цифровой, фазовый детектор, в котором пара
сигнала на его выходе без учета переброса фазовой задержки описывается
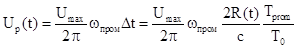 .
.
Выходная характеристика ФД в общем виде (без
учета переброса фаз) отображает линейную периодическую функцию в виде прямоугольного
треугольника, периодичность которой равна 2p. Сигнал на выходе ФД
зависит от фазовой задержки Dt и крутизны 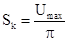 . Здесь -
. Здесь - 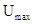 максимальное
значение сигнала дискриминационной характеристики цифрового фазового детектора,
максимальное
значение сигнала дискриминационной характеристики цифрового фазового детектора,
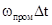 фазовая
задержка отраженного сигнала по отношению к опорному колебанию на промежуточной
частоте, ±p- значение перебрасываемой фазы. Значение фазовой
задержки находится путем нормировки выходного сигнала ФД- Ui к крутизне-
фазовая
задержка отраженного сигнала по отношению к опорному колебанию на промежуточной
частоте, ±p- значение перебрасываемой фазы. Значение фазовой
задержки находится путем нормировки выходного сигнала ФД- Ui к крутизне- 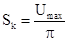 фазовой характеристики,
т.е.
фазовой характеристики,
т.е.
jpad=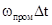 =
=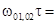
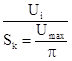 .
.
Например: Пусть
дальность измерения R(t)max
= 2000м; промежуточная частота, соответствующая
циклу однозначного измерения wprom = 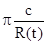 = 466 кГц;
интервал измеряемой задержки, приходящийся на дистанцию R(t)max=2000м равен
= 466 кГц;
интервал измеряемой задержки, приходящийся на дистанцию R(t)max=2000м равен 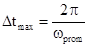 =1110-6с
»11мкс;
временной интервал измерения задержки R(t)min
= 2м, приходящейся на погрешность измерения дистанции
-
=1110-6с
»11мкс;
временной интервал измерения задержки R(t)min
= 2м, приходящейся на погрешность измерения дистанции
-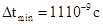 .
.
Если
измерять нормированную разницу амплитуд (Umax=5B), получаемую в процессе
переброса фаз опорного колебания на p, то можно из выражения
для квадратурной составляющей сигнала на выходе ФД
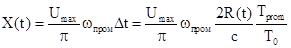
перейти
к уравнению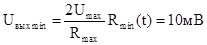 . Эта величина соответствует нижнему порогу
квантования большинства типов АЦП. Здесь Т0 выбираем из условия
. Эта величина соответствует нижнему порогу
квантования большинства типов АЦП. Здесь Т0 выбираем из условия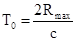 . Таким образом, такая модель построения системы
отсчета текущей дальности по точности не уступает прямому цифровому методу
измерения фазы.
. Таким образом, такая модель построения системы
отсчета текущей дальности по точности не уступает прямому цифровому методу
измерения фазы.
9.4.3.
Измерение профиля рельефа при двухчастотном
излучении
Во многих задачах объемного распознавания
возникает проблема измерения параметров рельефа, когда с относительно высокой
точностью и с высоким угловым разрешением требуется регистрировать координаты
рельефа (например, при определении на
ЖД линии мешающих предметов и в случае наличия определенного изгиба линии ). Возможны несколько методов обработки
информации:
· Для неподвижных объектов
осуществляют растровое сканирование
лазерной системой подсвета, с диаметром пучка равным разрешающей способности
системы в плоскости сканирования.
· Для подвижных объектов и
при скоростных измерениях область исследуемого рельефа или его части облучается
широким световым пучком, а разрешение по плоскости подсвета достигается применением сканирующего
фотоприемника или специально организованной матрицы.
С точки зрения сохранения однозначного
отсчета высоты рельефа и обеспечения высокой точности его измерения рельефа здесь лучше походят
двухчастотные методы дальнометрии. При этом процесс измерений можно проводить
по разностной частоте двух коррелированных когерентных несущих, что ,как будет
показано далее, нетрудно реализовать на практике. Эту же процедуру можно
получить на основе фазового метода дальнометрии с применением коррелированной
амплитудной модуляции на двух некогерентных несущих. Если при этом
ставится ещё задача получения трехцветного
изображения, то область рельефа необходимо подсвечивать трех цветовым пучком
(синий, зеленный, красный) при наличии соответствующей амплитудной модуляции.
Естественно, возникает желание упростить процедуру или алгоритм обработки
информации. Такие решения можно реализовать для подвижных целей при обработки
соответствующих доплеровских составляющих, в которых две рядом стоящие
компоненты при смешивании дают значение высоты рельефа. Подобные решения представлены
в главе 5.
Рассмотрим общие принципы определения
рельефа, которые можно уяснить из анализа рис.9.19 Пусть объект облучается сканирующим
пучком с точками выборки а, е. Требуется найти приращение рельефа DН = ак = de от линии отсчета аd. Здесь для рассмотрения принято
оа=оb,
как радиусы окружности; R(t)1, R(t)2 - длины линий визирования, R(t)1 = R01 - принятое исходное
положение отсчета, be=DH2,
q
-
угол отклонения луча от исходного положения.
Рис.9.19
Расчетные соотношения
Порядок измерения рельефа состоит в
следующем. В процессе обзора по двум точкам дальностей находим приращение дистанции DН2= R(t)2 - R(t)1, по которому
определяем высоту рельефа в точке его регистрации -DН. Так как cd = ra= Ro1- R01cosq = R01(1
-
cosq),
то из треугoльника
bce
имеем DН2 cosq
-
R01(1
-
cosq)
= DН,
где R01
= R(t)1. Т.е. высота
рельефа однозначно связана с приращением наклонной дальности и в дальнейшем в
алгоритмах будем находить только приращение.
9.4.4. Измерение рельефа по фазе эталонного тарированного
гетеродина
В плечо гетеродина вводится тарированный
фазовращатель jг = var. Опорный сигнал в этом случае
может быть представлен
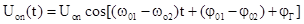 .
.
Если
учесть, что при приёме двухчастотного сигнала на выходе фотоприемника получаем
промежуточную частоту с указанными фазовыми соотношениям
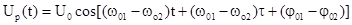 ,
,
то
результирующий сигнал на выхода фазовращателя равен
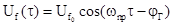 .
.
С
помощью перестраиваемого гетеродина добиваемся условия, когда cos jS
= 0, т.е. когда wnpt-jГ
= p/2, отсюда
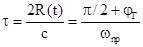 .
.
По
двум точкам измерений фиксируется приращение
рельефа.
9.4.5. Измерение рельефа при наличии
неоднозначности фазового отсчета
Постановка
задачи состоит в том, что излучаются два колебания с амплитудной
модуляцией с относительно небольшим разбросом частот модуляции. При приеме
каждая из них при выделении фазы путем сравнения с опорным каналом дает
неоднозначный отсчет регистрируемой дальности. Стоит задача устранения
неоднозначности измерений путем сравнительного анализа полученных конечных
отрезков фазовых измерений. В общем случае
дальность до объекта в условиях неоднозначного отсчет определяется R=n1l1+DR1; R=n2l2+DR2,
где n1,
n2-число
периодов неоднозначного отсчета; DR1;
DR2-остаточные
значения дальностей, получаемых по остаточным фазовым измерениям для каждой из
излучаемых частот. Если временные интервалы конечных фазовых измерений
находятся в пределах времени распространения излучения в пределах усредненной
длины волны, то можно принять, что n1=n2. В этом случае число
циклов неоднозначного отсчета равна
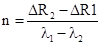 ,
,
а дальность до объекта по
конечным измерениям может быть определена R=n1l1+DR1 или R=n2l2+DR2.