6. Системы локации с шумовой
модуляцией
6.1 Структура отраженного
сигнала
Принцип работы такой системы базируется на
следующей последовательности операций [123,124]. Генератор белого шума в системе
имеет гауссово распределение амплитуд. Полоса шумового процесса ограничивается
коммутирующими цепями излучателя. Ограниченный белый шум модулирует несущую
частоту излучателя. Отраженный от цели сигнал, задержанный на время прохождения
изменяющегося во времени расстояния между целью и дальномерной системой (туда и
обратно), а также сигнал передатчика поступают на балансный смеситель (или
систему когерентного суммирования), в котором осуществляется их взаимно
корреляционная обработка. Максимум функции корреляции приходится или на фиксируемую
дистанцию или на нулевую дальность. Рассмотрим особенности структуры
сигналов и рациональные схемы построения
подобных систем. Спектр результирующего
сигнала рассмотрим по аналогии с ЧМ, но с некоторой модификацией. Если частота излученного
сигнала изменяется по закону
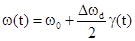 ,
, 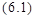
где 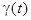 - модулирующая
функция частоты по закону шумового процесса, то изменение фазы определяется
соотношением:
- модулирующая
функция частоты по закону шумового процесса, то изменение фазы определяется
соотношением:
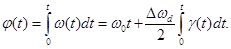
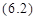
Излученный сигнал представим:
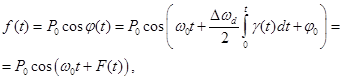 (6.3)
(6.3)
где 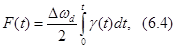 -
-
модулирующая функция изменения фазы по случайному
закону.
Фаза
отражённого сигнала, частота которого промодулирована по cлучайному
закону изменения амплитуды или периода появления выбросов модулирующего шума,
находится
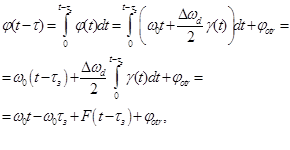
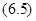
где 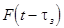 - модулирующая функция фазы отражённого сигнала.
- модулирующая функция фазы отражённого сигнала.
Т.к . 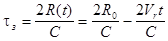 , (6.6)
, (6.6)
а 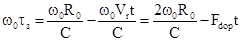 , где
, где 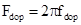 ,
,
то
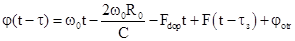 .
(6,7)
.
(6,7)
Отражённый сигнал представим в виде:
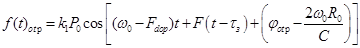 , (6,8)
, (6,8)
где 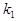 - коэффициент, учитывающий ослабление сигнала,
при отражении от лоцируемого объекта.
- коэффициент, учитывающий ослабление сигнала,
при отражении от лоцируемого объекта.
Для
фотоприемника достаточно найти амплитуду результирующего сигнала, как сумму
двух векторов
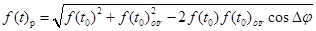 , (6,9)
, (6,9)
где:
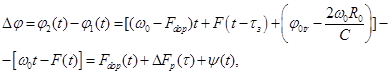 (6.10)
(6.10)
где
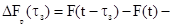 результирующая модулирующая функция;
результирующая модулирующая функция;
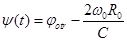 ,
(6.11)
,
(6.11)
результирующая модулирующая функция. Значение 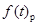 приведём к виду:
приведём к виду:
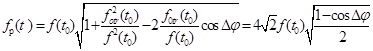 ,
(6,12)
,
(6,12)
на смесителе при
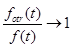 ,
, 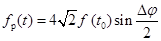
или
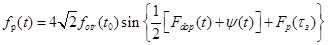 . (6,13)
. (6,13)
Полученное соотношение используется при интегральных
методах дальнометрии. Рассмотрим спектр результирующего сигнала. Для чего функцию
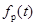 представим в следующем виде:
представим в следующем виде:
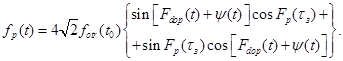 (6.14)
(6.14)
Найдем
выражение для результирующей модулирующей функции
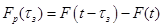 .
.
Модулирующая
функция частоты излучения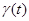 в функции
в функции 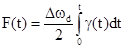 можно
представить в виде гармонического колебания со случайной амплитудой и со
случайной фазой
можно
представить в виде гармонического колебания со случайной амплитудой и со
случайной фазой
g(t)=A0noise(t)cosjnoise(t).
(6.15)
Здесь показано, что гармоническое колебание со случайной
амплитудой и случайной фазой образуют стационарный, но не эргодический процесс
(различные реализации обладают неодинаковой дисперсией). Однако для упрощения
расчетов остановимся на этой модели. Результирующая модулирующая функция
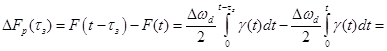
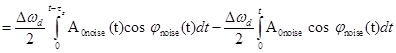 .
.
Здесь A0noise(t)-
рассматривается как форма сигнала единичных шумовых выбросов, нормированных к
максимальной амплитуде A0noise max(t0) и может быть представлена
в виде переменного коэффициента - k~, амплитуда которого
изменяется от 0 до1по случайному закону, например, нормальному. Будем считать,
что частота излучения изменяется в такт появления шумовых выбросов пропорционально
значению коэффициента k~,тогда
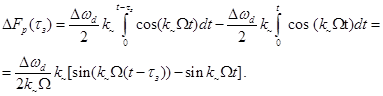 (6.16)
(6.16)
Если
в выбранном модулирующем сигнале одновременно (синхронно) изменяются по
случайному закону амплитуда и частота сигнала, то в амплитуде результирующей
модулирующей функции и как далее будет показана в амплитуде спектральных
составляющих результирующего спектра нет компонент, изменяющихся по случайному
закону. Учитывая, что
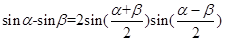 ,
,
имеем
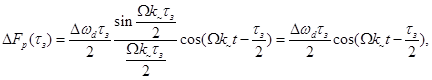
где при малом значении
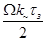 ®0, а
®0, а 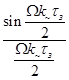 ®1,.
®1,.
Тогда
выражение (6.14) представим в следующем виде
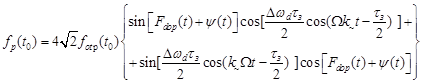 .
.
В теории бесселевых функций
доказываются следующие соотношения
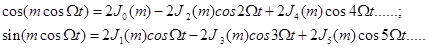
С помощью этих соотношений
получаем
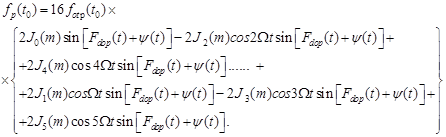
Учитывая, что
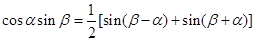 ,
,

При модуляции частоты излучения по сигналу с
изменяющейся амплитудой и фазой по случайному закону приводит к тому, что каждая
гармоническая составляющая спектра результирующего сигнала изменяет свою частоту также по случайному закону с сохранением
амплитуды гармонических компонент, определяемых
поведением соответствующей функции Бесселя (рис.5.5). Исключение составляет «нулевая гармоника», которая без
учета постоянной составляющей определяет поведение доплеровского сигнала. Из
расчетов и рисунка следует, что при гармоническом разложении результирующего
сигнала по функциям Бесселя имеет
место при малых задержках отраженного и
излученного сигналов, т.е. на интервале их взаимной корреляции (появляется) функция
Бесселя нулевого порядка, характеризуемая постоянной составляющей и не искаженным
(без гармоник) доплеровским сигналом. На остальных гармониках присутствует
широкополосный, шумоподобный сигнал с полосой равной девиации частоты.
6.2. Отличительные характеристики
результирующего сигнала при
шумовой модуляции
На выявленных признаках можно строить
помехоустойчивые дальномеры, когда максимум взаимокорреляционной функции формируется
на фиксируемой дистанции, которая регистрируется по переходу от шума к
гармонической составляющей и определяется в момент отсутствия нелинейных искажений в принятом
сигнале.
Рис.6.1. Датчик высоты с
шумовой модуляцией
Здесь 1 – шумовой генератор;2 – передатчик; 4 –
смеситель; 3, 5 – антенны; 6 – полосовой усилитель 7 – фильтр нижних частот; 8
– фильтр верхних частот; 9, 10 – детекторы-интеграторы; 11 – дифференциальный
усилитель.
Принцип
работы датчика высоты сводится к следующему. Полоса белого шума (генератор1)
модулирует несущую частоту передатчика 2.Модулированный сигнал излучается
антенной 3. Часть сигнала подается на смеситель 4 проходит через полосовой
усилитель 6, а затем поступает на фильтр нижних частот 7 и фильтр верхних частот
8. Частотная характеристика этого фильтра лежит в пределах от наивысшей
предполагаемой доплеровской частоты до
удвоенного значения этой частоты; частотная характеристика фильтра 7 включает
как самую низкую, так и самую высокую предполагаемую доплеровскую частоту.
Сигналы, прошедшие фильтры 7 и 8, поступа
ют соответственно
на детекторы-интеграторы 9 и 10.
При подаче
выходных сигналов от интеграторов 9, 10 на дифференциальный усилитель 11, в
котором выходной сигнал интегратора 10 вычитается из выходного сигнала
интегратора, получают функцию селекции по дальности, обозначенную кривой 12 (рис.6.2). На кривой 12 точка а обозначает приблизительный центр
когерентности сигнала, тогда как точки в и с соответствуют центрам сигнала, показанно
на рис.6.3 под скобой в и с.
Если
установить необходимое усиление детектора-интегратора, то выходной сигнал
дифференциального усилителя при небольших
дальностях будет иметь большое положительное значение (рис.6.4).
Если различие в величине усиления будет
существенным, то выходной сигнал усилителя при больших дальностях будет иметь относительно
небольшое отрицательное значение. Поэтому, если пороговая схема сконструирована
из расчета, что срабатывание детектора высоты будет происходить только от
сигнала дифференциального усилителя с положительным значением, может быть
достигнута абсолютная отсечка по дальности. При этом сигналы с отрицательным
значением при больших дальностях не будет влиять на перехват цели в пределах
зоны разрешения детектора дальности.
Здесь выходной сигнал смесителя усиливается
в полосовом усилителе (полоса усиления которого в двое превышает максимальное
значение доплеровской частоты); в результате чего когерентная и не когерентная
части сигналов усиливаются, а затем сравниваются. Если когерентная часть
сигнала превышает некогерентную на предварительно заданную величину, значит
цель в пределах зоны разрешения детектора дальности и необходим сигнал
срабатывания.
Представленная на рис.6.4 характеристика выходного
сигнала смесителя иллюстрирует изменение сигнала смесителя в зависимости от
дальности. При дальности до цели выходной сигнал представляет собой плавную
периодически изменяющуюся волну (участок
а ); при средней дальности до цели сигнал становится более
сложным (участок в) из-за “шума дальности”, наловившегося на эхо-сигнал.
По мере увеличения дальности эхо-сигнал превратится из плавного периодического
в некогерентный ВЧ сигнал, обусловленного “шумом дальности”.
6.3.
Корреляционная функция результирующего сигнала при шумовой
модуляции
С учетом проведенных
исследований следует, что в СД с шумовой
модуляцией по частоте излучения
зависимость напряжения на выходе смесителя от разности задержки 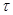 =tз отраженного от цели и гетеродинного сигнала можно описать
автокорреляционной функцией зондирующего сигнала. В нашем случае сигнал
представляет собой узкополосный процесс
=tз отраженного от цели и гетеродинного сигнала можно описать
автокорреляционной функцией зондирующего сигнала. В нашем случае сигнал
представляет собой узкополосный процесс
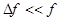 ,
, 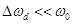 .
.
Автокорреляционную функцию узкополосного случайного ВЧ процесса
можно представить как
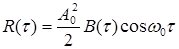 , ……. (6.17)
, ……. (6.17)
где 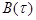 - огибающая автокорреляционной функции,
нормированная к единице. Определим её значение. Огибающая взаимно корреляционной
функции
- огибающая автокорреляционной функции,
нормированная к единице. Определим её значение. Огибающая взаимно корреляционной
функции 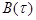 , частота которого модулирована нормальным случайным процессом, на выходе
смесителя с гауссовым фильтром равна
, частота которого модулирована нормальным случайным процессом, на выходе
смесителя с гауссовым фильтром равна
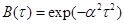 ,
,
где a- величина обратная постоянной инерционности избирательного
контура.
Энергетический спектр при этом определяется
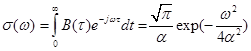 (6.18)
(6.18)
Эффективная ширина спектра F находится из соотношения..
Значение F = 2pf равно 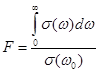 ,
,
где 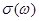 - спектральная плотность энергетического
спектра зондирующего сигнала,
- спектральная плотность энергетического
спектра зондирующего сигнала, 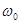 - центральная частота спектра
(несущая ).
- центральная частота спектра
(несущая ).
Значение F преобразуется к виду
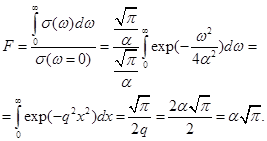
Подставив 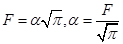 в
в 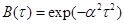 , получим
, получим
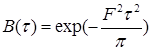 . (6.19)
. (6.19)
Рассмотрим
случай, когда максимум корреляционной функции
формируется на заданной дистанции
- R. Точность фиксации высоты в
этом случае может быть повышена за счет привязки точки отсчета к максимуму
корреляционной функции и сокращения времени корреляции.
Время задержки отраженного сигнала, соответственно
равно 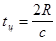 . Введем задержку гетеродинного сигнала
. Введем задержку гетеродинного сигнала 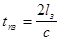 . Значение
. Значение 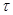 находим как
находим как 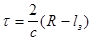 или
или
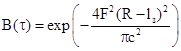 .(6.20)
.(6.20)
Измеряя В(t) по уровню 0,5 имеем 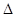 R=0,3
c/F. Например, для обеспечения
R=0,3
c/F. Например, для обеспечения 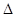 R=1м
необходима полоса модуляции
R=1м
необходима полоса модуляции 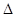 F=0,3.3.108=90
МГц.
F=0,3.3.108=90
МГц.