Содержание
Введение.. 3
Теоретическая
часть. 4
1.1 Средние величины в экономическом анализе.. 4
1.2 Условия применения средних величин в анализе.. 7
1.3 Виды средних величин. 9
1.3.1 Средняя арифметическая.. 11
1.3.2 Средняя гармоническая.. 14
1.3.3 Средняя геометрическая.. 17
1.3.4 Средняя квадратическая и средняя кубическая.. 17
1.3.5 Структурные средние.. 19
Расчетная
часть. 23
Аналитическая
часть. 29
Заключение.. 35
Список
литературы... 37
Введение
Данная курсовая работа
посвящена изучению метода средних величин. В средних величинах отображаются
важнейшие показатели, характеризующие общественные явления, такие как товарооборот,
товарные запасы, цены, заработная плата, рождаемость. Средними величинами
характеризуются качественные показатели коммерческой деятельности: издержки
обращения, прибыль, рентабельность и др. Правильное понимания сущности средней
через единичное и случайное позволяет выявить общее и необходимое, выявить
тенденцию закономерностей экономического
и социального развития. Метод средних величин находит свое применение
при статистических исследованиях в любой области.
В
теоретической части рассмотрим виды средних величин, а именно: средняя
арифметическая, средняя гармоническая, средняя геометрическая, средняя
квадратическая, средняя кубическая и структурные средние - в экономическом
анализе, а также условия их применения.
В
расчетной части представлены задачи на нахождение средних величин, на примере
этих задач будут показаны различные способы
нахождения средних величин, и использование их в экономическом анализе.
В
аналитической части будет проведено исследование в области дифференциации
заработной платы а так же анализ данных, рассчитанных с использованием метода
средних величин.
При
проведении статистического анализа данных в этой работе будут использованы
следующие программные средства: Microsoft
Word и Microsoft Excel.
Теоретическая часть
1.1 Средние величины в экономическом анализе
Статистика,
как известно, изучает массовые социально-экономические явления. Каждое из этих
явлений может иметь различное количественное выражение одного и того же
признака. Например, заработная плата одной и той же профессии рабочих или цены
на рынке на один и тот же товар и т.д. Средние
величины характеризуют качественные показатели коммерческой деятельности:
издержки обращения, прибыль, рентабельность и др.
Для
изучения какой-либо совокупности по варьирующим (количественно
изменяющимся) признакам статистика
использует средние величины.
Средняя величина – это
обобщающий показатель, характеризующий типичный уровень явления в конкретных
условиях места и времени, отражающий величину варьирующего признака в расчете
на единицу качественно однородной продукции.[1]
Количество показателей, вычисленных в виде средних величин, и используемых на
практике очень велико.
Важнейшее
свойство средней величины заключается в том, что она представляет значение
определенного признака во всей совокупности одним числом, несмотря на
количественные различия его у отдельных единиц совокупности, и выражает то
общее, что присуще всем единицам изучаемой совокупности. Таким образом, через
характеристику единицы совокупности она характеризует всю совокупность в целом.
Средние
величины связаны с законом больших чисел. Суть этой связи заключается в том,
что при осреднении случайные отклонения индивидуальных величин в силу действия
закона больших чисел взаимопогашаются и в средней выявляется основная тенденция развития, необходимость,
закономерность, однако, для этого среднюю необходимо вычислять на основе
обобщения массы фактов.
Средние
величины позволяют сравнивать показатели, относящиеся к совокупностям с
различной численностью единиц. Важнейшим условием научного использования
средних величин в статистическом анализе общественных явлений является
однородность совокупности, для которой исчисляется средняя. Одинаковая по форме
и технике вычисления средняя в одних
условиях (для неоднородной совокупности)
фиктивная, а в других (для однородной совокупности) соответствует
действительности.
Качественная
однородность совокупности определяется на основе всестороннего теоретического
анализа сущности явления. Так, например, при исчислении средней урожайности
требуется, чтобы исходные данные относились к одной и той же культуре (средняя
урожайность пшеницы) или группе культур (средняя урожайность зерновых). Нельзя
вычислять среднюю для разнородных культур.
Таким образом, основными свойствами
средней величин являются:
- Она обладает
устойчивостью, что позволяет выявлять закономерности развития явлений. Средняя облегчает сравнение двух
совокупностей, обладающих различной численностью.
- Она
помогает характеризовать развитие уровня явления во времени.
- Она
помогает выявить и охарактеризовать связь между явлениями.
Признак, по которому
производится осреднение, называется осредняемым признаком. Величина осредняемого признака у каждой
единицы совокупности называется ее индивидуальным значением.
Значение
признака, которое встречается у групп единиц или у отдельных единиц и не
повторяется, называется вариантом признака.
Средняя величина может принимать такие значения, которые не
присущи непосредственно ни одному из элементов изучаемой совокупности, кроме
того, на практике часто средняя величина для дискретного признака выражается
как для непрерывного. Например, среднее число родившихся на каждую тысячу
населения в регионе: в регионе имеются несколько населенных пунктов, в каждом
из которых складывается собственный уровень рождаемости. Чтобы рассчитать
среднюю рождаемость по региону необходимо численность всех родившихся младенцев
соотнести с численностью населения и умножить на 1000:
Результат расчета средней величины по данному показателю
может выражаться в дробных числах, несмотря на то, что показатель «число
родившихся» является целым числом.
Средняя
величина является равнодействующей всех факторов, оказывающих влияние на
изучаемое явление. То есть, при расчете средних величин взаимопогашаются
влияние случайных (пертурбационных, индивидуальных) факторов и, таким образом,
возможно определение закономерности, присущей исследуемому явлению. Значение
метода средних величин состоит в возможности перехода от единичного к общему,
от случайного к закономерному, существование средних величин является
категорией объективной действительности.
Итак,
к расчету средней предъявляются два
основных требования:
- Среднюю нужно рассчитывать так, чтобы она
погашала то, что мешает выявлению характерных черт и закономерностей в развитии
явления, а не затушевывала развитие.
- Средняя может быть вычислена только для
однородной совокупности. Средняя, вычисленная для неоднородной совокупности,
называется огульной.
Одинаковые по форме и
технике вычисления средние в одних случаях могут быть огульными, а в других –
общими в зависимости от того, с какой целью они интерпретируются.
Говоря
о методологии исчисления средних, не надо забывать, что средняя всегда дает
обобщенную характеристику лишь по одному признаку. Каждая же единица
совокупности имеет много признаков. Поэтому необходимо рассчитывать систему
средних, чтобы охарактеризовать явление со всех сторон.
Расчет средних величин
производится по правилам, которые разрабатываются математической статистикой.
Математические
приемы, используемые в различных разделах статистики, непосредственно связаны с
вычислением средних величин.
Средние
в общественных явлениях обладают относительным постоянством, т.е. в течение
какого-то определенного промежутка времени однотипные явления характеризуются
примерно одинаковыми средними.
1.2
Условия
применения средних величин в анализе
Как уже говорилось
выше, обязательным условием расчета средних величин для исследуемой
совокупности является ее качественная
однородность. Действительно, допустим, что отдельные элементы совокупности,
вследствие подверженности влиянию некоторого случайного фактора, имеют слишком
большие (или слишком малые) величины изучаемого признака, существенно
отличающиеся от остальных. Такие элементы повлияют на размер средней для данной
совокупности, поэтому средняя не будет выражать наиболее характерную для
совокупности величину признака.
Средняя
представляет собой обобщающую статистическую характеристику, в которой получает
количественное выражение типичный уровень признака, которым обладают члены
изучаемой совокупности. Но одной средней нельзя отобразить все характерные
черты статистического распределения. Возможны случаи совпадения средних
арифметических при разном характере распределения.
Показатели
вариации используются для характеристики и упорядочения статистических совокупностей.
Вариация – это различие в значениях какого-либо признака у разных единиц данной
совокупности в один и тот же период. Изучение вариации помогает понять сущность
изучаемого явления. К показателям вариации относятся размах вариации, среднее
линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент
вариации.
Если исследуемое явление не является однородным, то его
разбивают на группы, содержащие однородные элементы. Для такого явления
рассчитываются сначала средние по группам, которые называются групповые
средние, – они будут выражать наиболее типичную величину явления в каждой
группе. Затем рассчитывается для всех элементов общая средняя величина,
характеризующая явление в целом, – она рассчитывается как средняя из групповых
средних, взвешенных по числу элементов совокупности, включенных в каждую
группу.
На практике, однако, безусловное выполнение данного условия
повлекло бы за собой ограничение возможностей статистического анализа
общественных процессов. Поэтому, часто средние величины рассчитываются по
неоднородным явлениям. Например, при расчете величины средней заработной платы
по Тюменской области, когда совместно анализируется заработная плата труда в
автономных округах и в южных районах Тюменской области, а затем полученный
средний уровень заработной платы труда сопоставляется с соседними сибирскими
регионами.
Еще одним важным условием применения средних величин в
анализе является достаточное количество единиц в совокупности, по которой
рассчитывается среднее значение признака. Достаточность анализируемых единиц
обеспечивается корректным определением границ исследуемой совокупности, т.е.
закладывается еще на начальном этапе статистического исследования. Данное
условие становится решающим при применении выборочного наблюдения, когда
необходимо обеспечить репрезентативность выборки.
Определение максимального и минимального значения признака в
изучаемой совокупности также является условием применения средней величины в
анализе. В случае наличия больших отклонений между крайними значениями и
средней необходимо проверить принадлежность экстремумов к исследуемой
совокупности. Если сильная изменчивость признака вызвана случайными,
кратковременными факторами, то, возможно, крайние значения не характерны для
совокупности. Следовательно, их необходимо исключить из анализа, т.к. они
оказывают влияние на размер средней величины.
1.3
Виды средних
величин.
В
статистике выделяют несколько видов средних величин, структурированных по
разным основаниям:
1. По
наличию признака-веса:
а)
невзвешенная средняя величина;
б)
взвешенная средняя величина.
2. По форме
расчета:
а) средняя
арифметическая величина;
б) средняя
гармоническая величина;
в) средняя
геометрическая величина;
г) средняя
квадратическая, кубическая и т.д. величины.
3. По
охвату совокупности:
а)
групповая средняя величина;
б) общая
средняя величина.
Средние
величины различаются в зависимости от учета признаков, влияющих на осредняемую
величину:
Если
средняя величина рассчитывается для признака, без учета влияния на него
каких-либо других признаков, то такая средняя величина называется средней
невзвешенной или простой средней.
Если
имеются сведения о влиянии на осредняемый признак некоторого признака или
нескольких признаков, которые необходимо учесть при расчете для корректного
расчета средней величины, то рассчитывается средняя взвешенная.
По форме
расчета выделяют несколько видов средних величин, которые образованы из единой
степенной средней величины. Степенная средняя величина имеет форму:
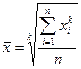 ,
,
где 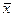 - среднее значение исследуемого явления;
- среднее значение исследуемого явления;
k –
показатель степени средней;
x – текущее значение (вариант) осредняемого признака;
i –i-тый
элемент совокупности;
n – число
наблюдений (число единиц совокупности).
При разных
показателях степени k получаем, соответственно, различные по форме средние
величины. (Табл. 1):
Таблица 1 - Наименования средних
величин по степеням средних.
|
Степень
средней
величины (k)
|
Название
средней
|
|
-1
|
гармоническая
|
|
0
|
геометрическая
|
|
1
|
арифметическая
|
|
2
|
квадратическая
|
|
3
|
кубическая
|
Выбор формы средней обусловлен исходным соотношением, суть
которого приводилась выше. Существует порядок расчета средней величины:
1.
Определение исходного соотношения для исследуемого показателя.
2.
Определение недостающих данных для расчета исходного соотношения.
3. Расчет
средней величины.
Рассмотрим
некоторые виды средних, которые наиболее часто используются в статистике. Для этого
введем следующие понятия и обозначения:
Признак,
по которому находится средняя, называемый осередняемым признаком, обозначим буквой "х"
Значения признака, которые встречаются у группы единиц или
отдельных единиц совокупности (не повторяясь) называются вариантами
признака и обозначаются через x
1, x
2, x
3 и т.д.
Средняя величина этих значений обозначается через " " .
1.3.1 Средняя
арифметическая
Средняя
арифметическая простая (невзвешенная) равна сумме отдельных значений признака,
деленной на число этих значений.
Отдельные
значения признака называют вариантами и обозначают через х (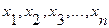 ); число единиц совокупности обозначают через n, среднее
значение признака - через
); число единиц совокупности обозначают через n, среднее
значение признака - через 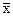 . Следовательно, средняя арифметическая простая равна:
. Следовательно, средняя арифметическая простая равна:
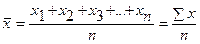
Например, имеются следующие данные о производстве
рабочими продукции (табл. 2)
Таблица 2 - Количество изделий, выпущенных за
смену
|
№ раб.
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
Выпущено изделий за смену
|
16
|
17
|
18
|
17
|
16
|
17
|
18
|
20
|
21
|
18
|
В
данном примере варьирующий признак - выпуск продукции за смену.
Численные
значения признака (16, 17 и т. д.)
называют вариантами. Определим среднюю выработку продукции рабочими данной
группы:
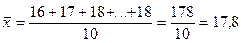
Простая
средняя арифметическая применяется в случаях,
когда имеются отдельные значения признака, т.е. данные не сгруппированы. Если данные
представлены в виде
рядов распределения или группировок,
то средняя исчисляется иначе.
Средняя
арифметическая взвешенная вычисляется по формуле 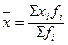 , где fi - частота
повторения i-ых
вариантов признака, называемая весом. Таким образом, средняя арифметическая
взвешенная равна сумме взвешенных вариантов признака, деленная на сумму весов.
, где fi - частота
повторения i-ых
вариантов признака, называемая весом. Таким образом, средняя арифметическая
взвешенная равна сумме взвешенных вариантов признака, деленная на сумму весов. 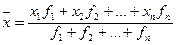 Она применяется в тех
случаях, когда каждая варианта признака встречается несколько (неравное) число
раз.
Она применяется в тех
случаях, когда каждая варианта признака встречается несколько (неравное) число
раз.
Статистический
материал в результате обработки может быть
представлен не только в виде дискретных рядов распределения, но и в виде интервальных вариационных рядов с
закрытыми или открытыми интервалами. В таких рядах условно величина интервала
первой группы принимается равной величине интервала последующей, а величина
интервала последней группы - величине интервала предыдущей. Дальнейший расчет
аналогичен изложенному выше.
При
расчете средней по интервальному вариационному ряду необходимо сначала найти
середину интервалов. Это и будут значения xi, а количество единиц совокупности в каждой группе fi (таблица 3).
Таблица 3 - Распределения
числа рабочих цеха по возрасту.
|
Возраст рабочего, лет
|
Число рабочих, чел (fi)
|
Середина возрастного
интервала, лет (xi)
|
|
20-30
30-40
40-50
50-60
60 и более
|
7
13
48
32
6
|
25
35
45
55
65
|
|
Итого
|
106
|
Х
|
Средний
возраст рабочих цеха будет равен 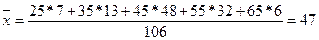 лет.
лет.
Для упрощения расчета
средней используют «способ моментов» (способ отсчета от условного нуля).
Способ
моментов предполагает следующие действия:
- Если возможно, то
уменьшаются веса.
-
Выбирается начало отсчета – условный нуль. Обычно выбирается с таким расчетом,
чтобы выбранное значение признака было как можно ближе к середине
распределения. Если распределение по своей форме близко к нормальному, но за
начало отсчета выбирают признак, обладающий наибольшим весом.
-
Находятся отклонения вариантов от условного нуля.
-
Если эти отклонения содержат общий множитель, то рассчитанные отклонения
делятся на этот множитель.
Находится среднее значение признака по следующей формуле
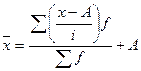 ,
,
где A - значение
одного из центральных вариантов с наибольшей частотой
i - величина
интервала.
Пример: А=
45; i=10
Таблица
4 - Распределение рабочих по возрасту.
|
Возраст рабочего, лет
|
Число рабочих, чел (fi)
|
Середина возрастного
интервала, лет (xi)
|
x1=
(x-A)/i
|
x1f
|
|
20-30
30-40
40-50
50-60
60 и более
|
7
13
48
32
6
|
25
35
45
55
65
|
-2
-1
0
1
2
|
-14
-13
0
32
12
|
|
Итого
|
106
|
Х
|
|
17
|
x1 – новые варианты признака
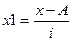 .
.
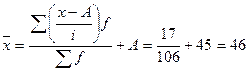 .
.
Как
видно из примера средняя величина, полученная в результате использования
способа моментов отличается от средней, рассчитанной по формуле взвешенной
средней. Неточность объясняется, по-видимому, предположением о равномерном
распределении единиц признака внутри группы, а так же большим интервалом.
В практике экономической статистики иногда
приходится исчислять среднюю по групповым средним или по средним отдельных
частей совокупности (частным средним). В таких случаях за варианты (х)
принимаются групповые или частные средние, на основании которых исчисляется
общая средняя как обычная средняя арифметическая взвешенная.
Средняя
арифметическая обладает рядом свойств:
1.
От уменьшения или увеличения частот каждого значения признака х в n раз величина средней арифметической не изменится.
Если
все частоты разделить или умножить на какое-либо число, то величина
средней не изменится.
2.
Общий множитель индивидуальных значений
признака может быть вынесен за знак средней:
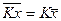
3.
Средняя суммы (разности)
двух или нескольких величин равна
сумме (разности) их средних:
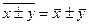
4.
Если х = с, где с - постоянная величина, то 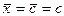 .
.
5.
Сумма отклонений значений признака Х от средней арифметической х равна нулю:
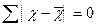
1.3.2 Средняя гармоническая
Наряду
со средней арифметической, в статистике применяется средняя гармоническая
величина, обратная средней
арифметической из обратных значений признака. Как и средняя арифметическая,
она может быть простой и взвешенной. Применяется она тогда, когда
необходимые веса (fi) в
исходных данных не заданы непосредственно, а входят сомножителем в одни из
имеющихся показателей.
Средняя
гармоническая простая рассчитывается по формуле
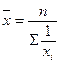 ,
,
т.е.
это обратная величина средней арифметической простой из обратных значений
признака.
Например,
бригада токарей была занята обточкой одинаковых деталей в течение 8-часового
рабочего дня. Первый токарь затратил на одну деталь 12 мин, второй - 15
мин., третий - 11, четвертый - 16 и
пятый - 14 мин. Определите среднее время, необходимое на изготовление одной
детали.
На
первый взгляд кажется,
что задача легко решается по формуле средней арифметической простой:
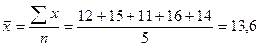
Полученная
средняя была бы правильной, если бы
каждый рабочий сделал только по
одной детали. Но в течение дня
отдельными рабочими было изготовлено различное число деталей. Для определения числа деталей, изготовленных
каждым рабочим, воспользуемся следующим соотношением:
все затраченное время
Среднее
время, затраченное =
--------------------------------------
на одну деталь число деталей
Число
деталей, изготовленных каждым рабочим, определяется отношением всего времени
работы к среднему времени, затраченному на одну деталь. Тогда среднее
время, необходимое для изготовления
одной детали, равно:
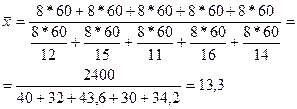
Это
же решение можно представить иначе:
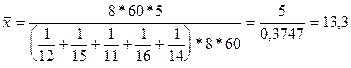
Таким
образом, формула для расчета средней
гармонической простой будет иметь вид:
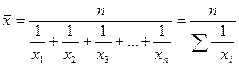
Средняя
гармоническая взвешенная:
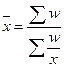 , где f=w/x
, где f=w/x
Например,
необходимо определить среднюю цену 1 кг картофеля по трем коммерческим
магазинам (таблица 5):
Таблица 5 - Цена и выручка от
реализации по трем коммерческим магазинам.
|
Номер магазина
|
Цена картофеля руб./кг, х
|
Выручка от реализации, млн
руб.,
w
|
Частота (количество
реализованных единиц), кг
f=w/x
|
|
1
2
3
|
800
1000
900
|
24
15
18
|
30000
15000
20000
|
|
Итого
|
-
|
57
|
65000
|
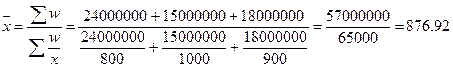
Исчисление
средней гармонической взвешенной освобождает от необходимости предварительного
расчета весов, поскольку эта операция
заложена в саму формулу.
1.3.3 Средняя геометрическая
Средняя
геометрическая применяется в тех случаях, когда индивидуальные значения
признака представляют собой, как правило, относительные величины динамики,
построенные в виде цепных величин, как отношение к предыдущему уровню
каждого уровня в ряду динамики, т.е. характеризует средний коэффициент роста.
Средняя
геометрическая исчисляется извлечением корня степени и из произведений
отдельных значений — вариантов признака х:
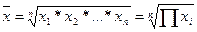
где
n — число вариантов;
П
— знак произведения.
Наиболее широкое применение
средняя геометрическая получила для определения средних темпов изменения в
рядах динамики, а также в рядах распределения.
1.3.4 Средняя квадратическая и средняя
кубическая
В ряде случаев в экономической практике возникает потребность
расчета среднего размера признака, выраженного в квадратных или кубических
единицах измерения. Тогда применяется средняя квадратическая (например, для
вычисления средней величины стороны и квадратных участков, средних диаметров
труб, стволов и т.п.) и средняя кубическая (например, при определении средней
длины стороны и кубов).
Средняя квадратическая простая является квадратным
корнем из частного от деления суммы квадратов отдельных значений признака на их
число:
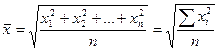 ,
,
где x1,x2,…xn- значения признака, n- их число.
Средняя квадратическая взвешенная:
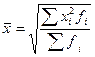 ,
,
где f-веса.
Средняя кубическая простая является кубическим корнем
из частного от деления суммы кубов отдельных значений признака на их число:
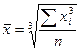 ,
,
где x1,x2,…xn- значения признака, n- их число.
Средняя кубическая взвешенная:
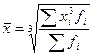 ,
,
где f-веса.
Средние квадратическая и кубическая имеют ограниченное
применение в практике статистики. Широко пользуется статистика средней
квадратической, но не из самих вариантов x, и из их отклонений от средней (х — 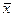 ) при расчете показателей вариации.
) при расчете показателей вариации.
Средняя
может быть вычислена не для всех, а для какой-либо части единиц совокупности.
Примером такой средней может быть средняя прогрессивная как одна из частных
средних, вычисляемая не для всех, а только для "лучших" (например,
для показателей выше или ниже сред- них индивидуальных).
1.3.5 Структурные
средние
Для
характеристики структуры вариационных рядов применяются так называемые
структурные средние. Наиболее часто используются в экономической практике мода
и медиана.
Мода – значение случайной величины встречающейся с наибольшей
вероятностью. В дискретном вариационном ряду это вариант имеющий наибольшую
частоту.
В
дискретных вариационных рядах мода определяется по наибольшей частоте.
Предположим товар А реализуют в городе 9 фирм по цене в рублях:
44;
43; 44; 45; 43; 46; 42; 46;43;
Так
как чаще всего встречается цена 43 рубля, то она и будет модальной.
В
интервальных вариационных рядах моду определяют приближенно по формуле
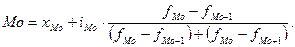 ,
,
где 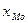 - начальное значение
интервала, содержащего моду;
- начальное значение
интервала, содержащего моду;
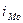 - величина модального
интервала;
- величина модального
интервала;
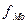 - частота модального
интервала;
- частота модального
интервала;
 - частота интервала,
предшествующего модальному;
- частота интервала,
предшествующего модальному;
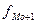 - частота интервала,
следующего за модальным.
- частота интервала,
следующего за модальным.
Место
нахождения модального интервала определяют по наибольшей частоте (таблица 6).
Таблица
6 - Распределение
предприятий по численности промышленно - производственного
персонала характеризуется следующими данными
|
Группы предприятий по
числу работающих, чел
|
Число предприятий
|
|
100 — 200
|
1
|
|
200 — 300
|
3
|
|
300 — 400
|
7
|
|
400 — 500
|
30
|
|
500 — 600
|
19
|
|
600 — 700
|
15
|
|
700 — 800
|
5
|
|
ИТОГО
|
80
|
В
этой задаче наибольшее число предприятий (30) имеет численность работающих от
400 до 500 человек. Следовательно, этот интервал является модальным интервалом
ряда распределения.
Введем
следующие обозначения:
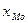 =400,
=400, 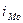 =100,
=100, 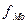 =30,
=30,  =7,
=7, 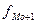 =19
=19
Подставим
эти значения в формулу моды и произведем вычисления:
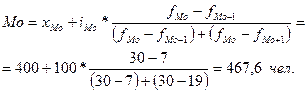
Мода
применяется для решения некоторых практических задач. Так, например, при
изучении товарооборота рынка берется модальная цена, для изучения спроса на
обувь, одежду используют модальные размеры обуви и одежды и др.
Медиана - это численное значение признака у той единицы
совокупности, которая находится в середине ранжированного ряда (построенного в
порядке возрастания, либо убывания значения изучаемого признака). Медиану
иногда называют серединной вариантой, т.к. она делит совокупность на две равные
части.
В
дискретных вариационных рядах с нечетным числом единиц совокупности - это
конкретное численное значение в середине ряда. Так в группе студентов из 27
человек медианным будет рост у 14-го,
если они выстроятся по росту. Если число единиц совокупности четное, то
медианой будет средняя арифметическая из значений признака у двух средних
членов ряда. Так, если в группе 26 человек, то медианным будет рост средний
13-го и 14-го студентов.
В
интервальных вариационных рядах медиана определяется по формуле:
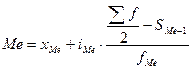 , где
, где
x0 - нижняя
гранича медианного интервала;
iMe - величина
медианного интервала;
Sme-1 - сумма
накопленных частот до медианного интервала;
fMe
- частота медианного интервала.
Пример:
Таблица
7 - Распределение предприятий по
численности промышленно производственного персонала характеризуется
следующими данными
|
Группы предприятий по
числу рабочих, чел.
|
Число предприятий
|
Сумма накопленных частот
|
|
100 — 200
|
1
|
1
|
|
200 — 300
|
3
|
4 (1+3)
|
|
300 — 400
|
7
|
11 (4+7)
|
|
400 — 500
|
30
|
41 (11+30)
|
|
500 — 600
|
19
|
—
|
|
600 — 700
|
15
|
—
|
|
700 — 800
|
5
|
—
|
|
ИТОГО
|
80
|
|
Определим
прежде всего медианный интервал. В
данной задаче сумма накопленных частот, превышающая половину всех значений
(41), соответствует интервалу 400 - 500.
Это и есть медианный интервал,
в котором находится медиана. Определим ее значение по приведенной выше
формуле.
Известно,
что:
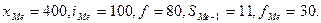
Следовательно,
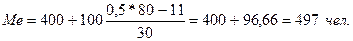
Cоотношение моды, медианы и средней
арифметической указывает на характер распределения признака в совокупности, позволяет
оценить его асимметрию. Если M0<Me< имеет место
правосторонняя асимметрия. Если же
имеет место
правосторонняя асимметрия. Если же  <Me<M0 - левосторонняя асимметрия ряда.
По приведенному примеру можно сделать заключение, что наиболее распространенная
численность рабочих является порядка 467,6 чел. В то же время более половины
предприятий имеют численность рабочих более 496,6 чел., при среднем уровне 510
чел.
<Me<M0 - левосторонняя асимметрия ряда.
По приведенному примеру можно сделать заключение, что наиболее распространенная
численность рабочих является порядка 467,6 чел. В то же время более половины
предприятий имеют численность рабочих более 496,6 чел., при среднем уровне 510
чел. 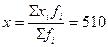 чел. Из соотношения
этих показателей следует сделать вывод о правосторонней асимметрии
распределения предприятий по численности промышленно - производственного
персонала.
чел. Из соотношения
этих показателей следует сделать вывод о правосторонней асимметрии
распределения предприятий по численности промышленно - производственного
персонала.
Мода
и медиана в отличие от степенных средних являются конкретными характеристиками,
их значение имеет какой-либо конкретный вариант в вариационном ряду.
Мода
и медиана, как правило, отличаются от значения средней, совпадая с ней только в
случае симметричного распределения частот вариационного ряда. Поэтому
соотношение моды, медианы и средней арифметической позволяет оценить ассиметрию
ряда распределения.
Мода
и медиана, как правило, являются дополнительными к средней характеристиками
совокупности и используются в математической статистике для анализа формы рядов
распределения.
Аналогично
медиане вычисляются значения признака, делящие совокупность на четыре равные
(по числу единиц) части — квартели, на пять равных частей — квинтели, на десять
частей — децели, на сто частей — перцентели.
Расчетная часть
Задание 9
1.
По первичным данным таблицы 8 определите среднегодовую
стоимость основных производственных фондов в расчете на одно предприятие.
2.
Постройте статистический ряд распределения предприятий
по среднегодовой стоимости основных производственных фондов, образовав 4 группы
предприятий с равными интервалами, охарактеризовав их числом предприятий и их удельным
весом.
По ряду
распределения рассчитайте среднегодовую стоимость основных производственных
фондов, взвешивая варианты признака: а) по числу предприятий, б) по удельному
весу предприятий.
Сравните
полученную среднюю с п. 1 и поясните их расхождение.
3.
Имеются данные о финансовых показателях предприятия
фирмы за отчетный период:
|
№ предприятия
|
Получено прибыли, тыс.руб.
|
Акционерный капитал, тыс.руб.
|
Рентабельность акционерного капитала, %
|
Удельный вес акционерного капитала в общем объеме, %
|
|
1
|
1512
|
5040
|
30
|
42
|
|
2
|
528
|
1320
|
40
|
11
|
|
3
|
1410
|
5640
|
25
|
47
|
Определите
средний процент рентабельности акционерного капитала фирмы, используя
показатели: а) гр.1 и гр.2; б) гр.2 и гр.3; в) гр.1 и гр.3; г) гр.3 и гр.4.
Таблица 8
– Среднегодовая стоимость ОПФ, млн.руб.
|
№ п/п
|
Среднегодовая стоимость
ОПФ
|
Выпуск продукции
|
|
А
|
1
|
2
|
|
1
|
27
|
21
|
|
2
|
46
|
27
|
|
3
|
33
|
41
|
|
4
|
35
|
30
|
|
5
|
41
|
47
|
|
6
|
42
|
42
|
|
7
|
53
|
34
|
|
8
|
55
|
57
|
|
9
|
60
|
46
|
|
10
|
46
|
48
|
|
11
|
39
|
45
|
|
12
|
45
|
43
|
|
13
|
57
|
48
|
|
14
|
56
|
60
|
|
15
|
36
|
35
|
|
16
|
47
|
40
|
|
17
|
20
|
24
|
|
18
|
29
|
36
|
|
19
|
26
|
19
|
|
20
|
49
|
39
|
|
21
|
38
|
35
|
|
22
|
37
|
34
|
|
23
|
56
|
61
|
|
24
|
49
|
50
|
|
25
|
37
|
38
|
|
26
|
33
|
30
|
|
27
|
55
|
52
|
|
28
|
44
|
46
|
|
29
|
41
|
38
|
|
30
|
28
|
35
|
Решение
1.Так как
имеются не группированные одиночные размеры признака (среднегодовая стоимость
ОПФ), то для определения среднего в
расчете на одно предприятие используем формулу средней арифметической простой:
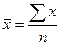 ,
,
где
х1, х2, … хn –
розничный товарооборот, n –
количество предприятий розничной торговли. Тогда:
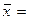
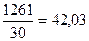 (млн.руб.),
(млн.руб.),
Ответ:
Среднегодовой размер ОПФ в расчете на одно предприятие равен 42,03 млн. руб..
Расчет производился по формуле средней арифметической простой.
2.
Построим статистический ряд распределения торговых предприятий по размеру среднегодовой
стоимости ОПФ, выделив 4 группы с равными интервалами.
Найдем
величину равного интервала по формуле:
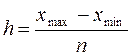 ,
,
где
xmax
и xmin
– максимальное и минимальное значение признака, n – число групп. Таким образом
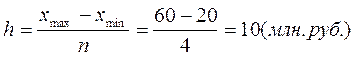 ,
,
где
xmax=60, xmin=20 – максимальное и минимальное
значение розничного товарооборота на предприятиях (млн. руб.), n=4 – количество групп.
Добавим
полученное значение величены интервала к
минимальному значению признака в группе и получим следующие группы предприятий
по значению розничного товарооборота
(табл.9)
Таблица 9 - Статистический
ряд распределения предприятий по размеру среднегодовой стоимости ОПФ
|
№ группы
|
Среднегодовая стоимость
ОПФ, млн. руб.
|
Число предприятий
|
Удельный вес предприятий
|
Центр интервала
|
|
х
|
f
|
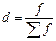
|
x’
|
|
1
|
20-30
|
5
|
0,17
|
25
|
|
2
|
30-40
|
8
|
0,27
|
35
|
|
3
|
40-50
|
10
|
0,33
|
45
|
|
4
|
50-60
|
7
|
0,23
|
55
|
|
Всего
|
30
|
1,0
|
|
По
данным ряда распределения рассчитаем среднегодовую стоимость ОПФ на одно предприятие, взвешивая значение
признака:
а) по числу предприятий (табл. 9.1)
Таблица 9.1 - Ряд распределения предприятий по размеру
среднегодовой стоимости ОПФ
|
№ группы
|
Среднегодовая стоимость
ОПФ, млн. руб.
|
Число предприятий
|
Центр интервала
|
x’f
|
|
Х
|
f
|
x’
|
x’f
|
|
1
|
20-30
|
5
|
25
|
125
|
|
2
|
30-40
|
8
|
35
|
280
|
|
3
|
40-50
|
10
|
45
|
450
|
|
4
|
50-60
|
7
|
55
|
385
|
|
Всего
|
30
|
|
1240
|
Воспользуемся
формулой средней арифметической взвешенной,
и выразим варианты дискретным числом, которое найдем как среднюю
арифметическую простую из верхнего и нижнего значения интервала (обозначен как
центр интервала х’).
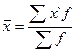 ; где
; где 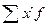 -сумма произведений среднегодовой стоимости ОПФ предприятий
на их количество,
-сумма произведений среднегодовой стоимости ОПФ предприятий
на их количество,  - общее число предприятий.
- общее число предприятий.
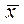 =
=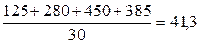 млн.руб.
млн.руб.
Ответ:
Средний размер среднегодовой стоимости ОПФ на одно предприятие, при взвешивании
значеняе варьирующего признака по числу предприятий составляет 41,3 млн. руб.
б)по
удельному весу предприятий (табл.9.2)
Таблица
9.2
|
№ группы
|
Среднегодовая стоимость
ОПФ, млн. руб.
|
Число предприятий
|
Удельный вес
|
Центр интервала
|
x’d
|
|
х
|
f
|
d
|
x’
|
x’d
|
|
1
|
20-30
|
5
|
0,17
|
25
|
3,5
|
|
2
|
30-40
|
8
|
0,27
|
35
|
9,45
|
|
3
|
40-50
|
10
|
0,33
|
45
|
14,85
|
|
4
|
50-60
|
7
|
0,23
|
55
|
12,65
|
|
Всего
|
30
|
1,0
|
|
40,45
|
Воспользуемся
формулой средней арифметической взвешенной, где
в качестве весов выступает удельный вес предприятия:
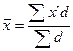 ; где
; где 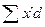 - сумма произведений размеров розничного товарооборота,
- сумма произведений размеров розничного товарооборота, 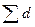 =1 – удельный вес.
=1 – удельный вес.
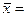 3,5+9,45+14,85+12,65 = 40,45 млн. руб.
3,5+9,45+14,85+12,65 = 40,45 млн. руб.
Погрешность=(Средняя
простая - Средняя взвешенная)/Средняя простая= (42,03-40,45)/42,03=0,038=3,8% -
допустимая погрешность.
Ответ:
Средний размер среднегодовой стоимости ОПФ на одно предприятие, при взвешивании значения варьирующего
признака по удельному весу предприятий
составляет 40,45 млн. руб.
Сравнивая
результаты, полученные в п.2 и п.1 обнаруживаем расхождение, которое можно
объяснить тем, что в п.1 проводится
расчет проводится по формуле средней арифметической простой в расчете на одно
предприятие, а в п.2 по формуле средней арифметической взвешенной по ряду
распределения предприятий по среднегодовой стоимости ОПФ с выделением четырех
групп. Для вычисления мы использовали средние значения в интервале. При таком
исчислении средней допускается погрешность до 5%, поскольку предполагается
равномерность распределения единиц признака внутри группы.
3.
Таблица 11 - Данные по
предприятиям
|
№ предприятия
|
Получено прибыли, тыс.руб.
|
Акционерный капитал, тыс.руб.
|
Рентабельность акционерного капитала, %
|
Удельный вес акционерного капитала в общем объеме, %
|
|
1
|
2
|
3
|
4
|
|
1
|
1512
|
5040
|
30
|
42
|
|
2
|
528
|
1320
|
40
|
11
|
|
3
|
1410
|
5640
|
25
|
47
|
Определим
средний процент рентабельности акционерного капитала фирмы, используя
показатели: а) гр.1 и гр.2; б) гр.2 и гр.3; в) гр.1 и гр.3; г) гр.3 и гр.4.
Средний процент
рентабельности исходя их группы 1 и 2 рассчитывается как:
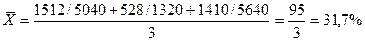
Средний процент
рентабельности исходя их группы 2 и 3 рассчитывается как:

Средний процент
рентабельности исходя их группы 1 и 3 рассчитывается как:
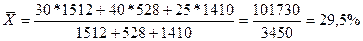
Средний процент
рентабельности исходя их группы 3 и 4 рассчитывается как:
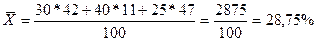
Аналитическая
часть
Аналитическая часть курсовой работы
посвящена исследованию анализа дифференциальной заработной платы с методом
средних величин. В ходе выполнения задания были использованы инструменты MS Excel.
На начало 2006 г. в крае насчитывалось 2,7 тыс. крупных и
средних предприятий. Согласно предоставленным данным, заработная плата в январе
в среднем составила 4,6 тыс. рублей, при этом на предприятиях работало 375 тыс. человек, что составило три
четверти занятого населения, половину трудоспособного населения.
Таблица12 - Распределение
работающих по уровню заработной платы
|
Численность
работающих, (человек)
|
Середина интервала
|
В % к общей
численности работающих
|
Кумулятивный
(накапливаемый процент)
|
|
Всего работающих:
|
374603
|
-
|
100,0
|
-
|
|
В том числе с
уровнем средней заработной платы на предприятии рублей:
до 1000
|
14758
|
500
|
3,9
|
3,9
|
|
1000-2000
|
90601
|
1500
|
24,2
|
28,1
|
|
2000-3000
|
79002
|
2500
|
21,1
|
49,2
|
|
3000-4000
|
41836
|
3500
|
11,2
|
60,4
|
|
4000-5000
|
30869
|
4500
|
8,2
|
68,6
|
|
5000-6000
|
25569
|
5500
|
6,8
|
75,4
|
|
6000-8000
|
40199
|
7000
|
10,7
|
86,1
|
|
8000-10000
|
23041
|
9000
|
6,2
|
92,3
|
|
10000-14000
|
15558
|
12000
|
4,2
|
96,5
|
|
Свыше 14000
|
13170
|
16000
|
3,5
|
100,0
|
Данные статистических наблюдений сообщают информацию о средней по предприятию заработной плате.
Дифференциацию оплаты труда по предприятиям можно проследить, если взвесить
среднюю заработную плату на численность работающих, то есть условно
распространить среднюю зарплату по предприятию на каждого, работающего на этом
предприятии.
Оценить общую картину распределения значений заработной платы
позволяет гистограмма (рис.1). Весь диапазон значений заработной платы, от
минимального до максимального, разделен на равные интервалы. Уровни столбцов
представляют списочную численность работников с определенным значением
заработной платы в данном интервале.
То есть, сравнительно небольшая численность работающих имеет довольно
высокую (по сравнению с основной массой) заработную плату.
Количество работающих по уровню
зарплаты распределилось следующим образом:
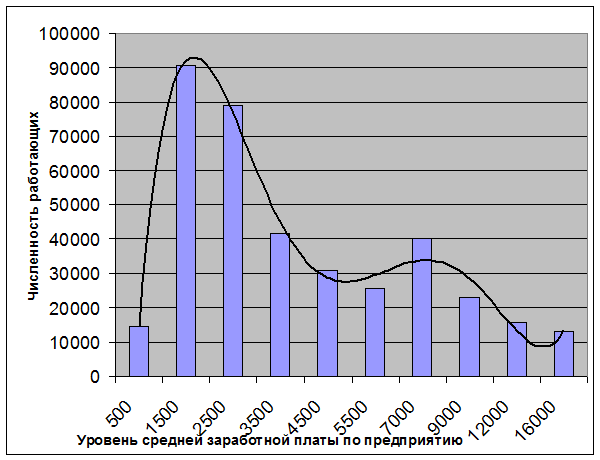
Рисунок 1 -
Распределение работающих по уровню заработной платы
Помимо этого в результате
расчетов были получены следующие данные: квартиль - составил в среднем по
предприятию – 1,9 тыс. руб., это граница в которой находится величина
заработной платы четверти самых низкооплачиваемых работающих. Медиана (в
среднем - 3,1 тыс. рублей) - значит половина
работающих получает зарплату, не превышающую этой суммы. Три четверти
работающих имеет зарплату, не больше 5,9 тыс. рублей в среднем по предприятиям.
В пределах 12,2 тыс. рублей получает
заработную плату большинство работающих. Экстремально высокие значения зарплаты
начисляются 5% работников.
Величина средней заработной платы на предприятиях в 2006 г. не превышала прожиточный минимум для
трудоспособного населения более чем на трети предприятий (в среднем по региону
он составил 1,9 тыс. рублей), на которых
была занята пятая часть работающего населения.
Таким образом, наблюдается
резкая дифференциация зарплаты в пределах городов и районов, а так же между ними. Имеются экстремально высокие
значения начисленной заработной платы, на порядок и более превышающие
минимальные размеры заработной платы. При этом минимальные уровни зарплаты не
представлены ни как выбросы, ни как экстремумы, то есть значения, явно
отличающиеся от основной их массы. Напротив, основная доля работающих имеет
довольно низкий уровень зарплаты. В среднем по региону пятая часть из них
получает заработную плату, не превышающую прожиточный минимум для
трудоспособного населения, а в ряде районов – это относится к половине и более
работающих. Заработная плата половины работающих не превышает 3,1 тыс. рублей.
Те, кто не относится ни к низко-, ни к высокооплачиваемым, получают в пределах
1,9-5,9 тыс. рублей. 66% работников получили заработную плату, составляющую 4,6
тыс. рублей – это ниже, чем средняя зарплата по региону.
Выявленные
пропорции позволяют предположить, что уровень средней зарплаты несколько завышен, если
оценивать основную массу работающих. Поэтому возникает необходимость применения
альтернативных показателей, характеризующих среднее значение заработной платы.
Одним
из них является медиана, величина которой приводилась выше и составляет 3,1
тыс. рублей.
Иногда для аналитических
целей используется 5%-ное усеченное среднее. Оно вычисляется путем
упорядочивания значений по возрастанию, отсечением (удалением) 5% значений от
начала и от конца, а затем - вычислением обычного среднего для оставшихся
значений. Как уже отмечалось, именно эта доля работающих на крупных и средних
предприятиях получает зарплату с экстремально высокими значениями. То есть
5%-ное усеченное среднее - более корректный показатель для данного исследования.
При расчете получаем, что по
региону он составил 4,1 тыс. рублей, что меньше средней зарплаты (4,6 тыс.), но
больше медианы.
И все
же, так как традиционно в аналитической работе используется среднее,
необходимость корректного вычисления этого показателя, с учетом того, что
оценка среднего очень чувствительна к экстремальным значениям, остается.
Вычисление
среднего, сравнение групповых средних допустимо только для переменных с так
называемым нормальным распределением. В существующей практике среднее вычисляется без проверки характера
распределения, хотя последнее может оказаться не похожим на нормальное, а это может привести к ошибочным выводам,
особенно когда распределение значительно отклоняется от нормального. Плотность
нормального распределения представляет симметричную кривую, в которой
численности растут до максимума, а потом с такой же постепенностью убывают.
Приведение данных к нормальному распределению заключается в преобразовании
исходных данных - логарифмировании, возведении в степень, извлечении корня и
т.п.
В
нашем случае кривая нормального распределения несимметрична, имеет длинный
правый отрезок, что видно на гистограмме (рис. 1). Для улучшения распределения
показателя «заработная плата» использовалось возведение в степень. После этого
было найдено среднее, 5%-ное усеченное среднее, медиана. Далее с ними были
произведены вычисления, обратные проведенным преобразованиям. В результате были
получены следующие значения (таблица 13):
Таблица13 - Показатели,
характеризующие средний уровень заработной платы
|
Заработная плата по региону, рублей
|
|
Среднее
|
5%-ное усеченное среднее
|
Медиана
|
|
До преобразования
|
4581
|
4044
|
3098
|
|
После преобразования
|
3349
|
3349
|
3097
|
Как видно из таблицы,
после преобразований значение медианы практически не изменилось, значения
среднего и 5%-ного усеченного среднего сравнялись и гораздо меньше стали
отличаться от медианы.
Таким образом, средняя
заработная плата по крупным и средним предприятиям составила 4,6 тыс. рублей,
однако для основной доли этих предприятий среднее намного ниже - 3,3 тыс.
рублей. Этот показатель больше соответствует действительности. К рассмотрению в
качестве средней заработной платы на крупных и средних предприятиях следует
принимать именно его.
Итак,
наблюдается существенная дифференциация уровней заработной платы, отражающая
процесс расслоения общества по величине доходов. Результаты аналитического
исследования показали, что применяемое в статистической практике среднее,
вычисляемое без проверки характера распределения данных, испытывает влияние
экстремальных значений, а значит, может искажать явления, происходящие в
обществе. Для получения более точных сведений об экономическом показателе
следует преобразовать данные и привести задачу к виду, близкому к нормальному закону. В противном случае
расчеты приведут к ошибочным показателям и неверным выводам.
Об
этой особенности следует помнить при вычислении социальных показателей,
характеризующих уровень жизни, где часто имеют место экстремальные значения показателей. В данном
конкретном случае хорошо заметно, что рассчитанная на основании исходных данных
средняя величина не характерна для основного числа исследуемых элементов.
Основные расчеты аналитической части удобно выполнить в среде MS Excel. Для этого исходные данные (средняя
заработная плата и численность работающих) вводятся в таблицу. После этого
создается рабочая таблица, которая
позволит произвести такие промежуточные вычисления как середина интервала, а
так же таблица распределения работающих
по уровню заработной платы.
Последовательно вводятся
необходимые для расчета и группировки
формулы. Основное удобство заключается в том, что, по сути, формула вводится
только один раз – все повторяющиеся действия выполняются компьютером в заданном диапазоне. Для построения
диаграммы достаточно выделить необходимые в построении данные и воспользоваться мастером диаграмм.
Заключение
Подводя
итог можно сказать, что область применения и использования средних величин в
статистике довольно широка.
Средние
величины — это обобщающие показатели, в которых находят выражения действие
общих условий, закономерность изучаемого явления. Статистические средние
рассчитываются на основе массовых данных правильно статистически
организованного массового наблюдения (сплошного или выборочного). Однако
статистическая средняя будет объективна и типична, если она рассчитывается по
массовым данным для качественно однородной совокупности (массовых явлений). Применение средних должно исходить из
диалектического понимания категорий общего и индивидуального, массового и единичного.
Средняя отражает то общее, что
складывается в каждом отдельном, единичном объекте, именно по - этому средняя
имеет большое значение для выявления закономерностей присущих массовым
общественным явлениям и незаметных в единичных явлениях.
Отклонение индивидуального от общего —
проявление процесса развития. В отдельных единичных случаях могут быть заложены
элементы нового, передового. В этом случае именно конкретных фактор, взятые на
фоне средних величин, характеризует процесс развития. Поэтому в средней и
отражается характерный, типичный, реальный уровень изучаемых явлений.
Характеристики этих уровней и их изменений во времени и в пространстве являются
одной из главных задач средних величин. Так, через средние проявляется,
например, изменение благосостояния населения находит свое отражение в средних
показателях заработной платы, доходов семьи в целом и по отдельным социальным
группам, уровня потребления продуктов, товаров и услуг.
Средний показатель — это значение
типичное (обычное, нормальное, сложившееся в целом), но таковым оно является
потому, что формируется в нормальных, естественных условиях существования
конкретного массового явления, рассматриваемого в целом. Средняя отображает
объективное свойство явления. В действительности часто существует только
отклоняющиеся явления, и средняя как явления может и не существовать, хотя
понятие типичности явления и заимствуется из действительности. Средняя величина является отражением
значения изучаемого признака и, следовательно, измеряется в той же размеренности
что и этот признак. Однако существуют различные способы приближенного
определения уровня распределения численности для сравнения сводных признаков,
непосредственно не сравнимых между собой, например средняя численность
населения по отношению к территории (средняя плотность населения). В
зависимости от того, какой именно фактор нужно элиминировать, будет находиться
и содержание средней.
Сочетание общих средних с групповыми
средними дает возможность ограничить качественно однородные совокупности.
Расчленяя массу объектов, составляющих то или иное сложное явления, на
внутренне однородные, но качественно различные группы, характеризуя каждую из
групп своей средней, можно вскрыть резервы процесс нарождающегося нового
качества. Например, распределения населения по доходу позволяет выявить
формирование новых социальных групп.
Список
литературы
- Бестужев-Лада И.В. Мир нашего завтра, М.: «Мысль», 2001. – 324с.
- Боярский А.Я., Громыко Г.Л. Общая теория статистики,
М.:Финансы и статистика, 2005. – 349с.
- Гусаров
В.М. Теория статистики. – М.:Инфра-М, 2003. – 432с.
- Российский
статистический ежегодник. – М.:2007.
- Статистический
словарь / Под. ред. Юркова Ю.А. - М.: Финстатинформ, 2006. – 709с.
[1] Гусаров В.М. Статистика:
Учеб. Пособие для вузов. – М.: ЮНИТИ-ДАНА, 2001. стр.60