Вариант № 17
Задание 1
Имеются следующие данные 25 заводов
одной из отраслей промышленности:
|
Номер завода
|
Среднегодовая стоимость
ОПФ, млн.руб.
|
Валовая продукция в
сопоставимых ценах, млн.руб.
|
|
1
|
5,9
|
7,6
|
|
2
|
5,3
|
7,0
|
|
3
|
3,9
|
4,4
|
|
4
|
4,2
|
5,9
|
|
5
|
5,7
|
4,9
|
|
6
|
4,6
|
5,9
|
|
7
|
4,3
|
4,7
|
|
8
|
6,2
|
8,5
|
|
9
|
6,5
|
7,4
|
|
10
|
2,1
|
2,2
|
|
11
|
6,6
|
7,8
|
|
12
|
4,2
|
4,2
|
|
13
|
8,0
|
10,6
|
|
14
|
5,1
|
5,8
|
|
15
|
4,9
|
5,3
|
|
16
|
4,3
|
4,9
|
|
17
|
5,8
|
6,0
|
|
18
|
7,2
|
10,4
|
|
19
|
6,6
|
6,9
|
|
20
|
3,0
|
3,6
|
|
21
|
6,8
|
7,3
|
|
22
|
3,5
|
3,6
|
|
23
|
3,2
|
3,4
|
|
24
|
3,6
|
3,6
|
|
25
|
4,2
|
4,6
|
С целью изучения зависимости между
среднегодовой стоимостью ОПФ и выпуском валовой продукции произведите
группировку заводов по среднегодовой стоимости ОПФ, образовав 4 группы заводов
с равными интервалами. По каждой группе и совокупности заводов подсчитайте:
1.
Число заводов.
2.
Среднегодовую стоимость ОПФ – всего и в среднем на
один завод.
3.
Стоимость валовой продукции – всего и в среднем на
один завод.
4.
Размер валовой продукции на один рубль ОПФ
(фондоотдачу).
Результаты представьте в
виде групповой таблицы. Сделайте выводы.
Решение
i = (maxОПФ – minОПФ)/k, где
i – величина интервала;
maxОПФ – максимальное значение среднегодовой стоимости основных
производственных фондов;
minОПФ – минимальное значение среднегодовой стоимости основных
производственных фондов;
k – количество интервалов.
i = (8,0 – 2,1)/4 = 1,475.
Рассчитаем границы интервалов:
1-й интервал: от 2,1 до 2,1 + 1,475,
т.е. от 2,1 до 3,575;
2-й интервал: от 3,575 до 3,575 +
1,475, т.е. от 3,575 до 5,05;
3-й интервал: от 5,05 до 5,05 + 1,475,
т.е. от 5,05 до 6,525;
4-й интервал: от 6,525 до 6,525 +
1,475, т.е. от 6,525 до 8.
1. 1-я группа заводов по среднегодовой
стоимости ОПФ состоит из 4-х заводов (№ 10, №20, №22, №23);
2-я группа заводов состоит из 9-ти
заводов (№3, №4, №6, №7, №12, №15, №16, №24, №25);
3-я группа заводов состоит из 7-ми
заводов (№1, №2, №5, №8, №9, №14, №17);
4-я группа заводов состоит из 5-ти
заводов (№11, №13, №18, №19, 21)
Общее число заводов во всех группах
равняется 25 (4+9+7+5 = 25).
2. Общая среднегодовая стоимость ОПФ
1-й группы заводов (ОССОПФ1) = сумма среднегодовых стоимостей ОПФ заводов в 1-й
группе = 2,1 + 3,0 + 3,5 + 3,2 = 11,8 млн. руб.
ОССОПФ2 = 3,9 + 4,2
+ 4,6 + 4,3 + 4,2 + 4,9 + 4,3 + 3,6 + 4,2 = 38,2 млн. руб.
ОССОПФ3 = 5,9 + 5,3
+ 5,7 + 6,2 + 6,5 + 5,1 + 5,8 = 40,5 млн. руб.
ОССОПФ4 = 6,6 + 8,0
+7,2 + 6,6 + 6,8 = 35,2 млн. руб.
Общая среднегодовая стоимость всех
заводов = сумма среднегодовых стоимостей ОПФ всей совокупности заводов = ОССОПФ1 + ОССОПФ2 +
ОССОПФ3 + ОССОПФ4 = 11,8 +
38,2 + 40,5 + 35,2 = 125,7 млн. руб.
Среднегодовая стоимость ОПФ в среднем
на один завод для 1-й группы заводов = сумма среднегодовых стоимостей ОПФ
заводов в 1-й группе / число заводов в 1-й группе = 11,8/ 4 = 2,95 млн. руб.
Среднегодовая стоимость ОПФ в среднем
на один завод для 2-й группы заводов = сумма среднегодовых стоимостей ОПФ
заводов во 2-й группе / число заводов во 2-й группе = 38,2/ 9 = 4,244 млн. руб.
Среднегодовая стоимость ОПФ в среднем
на один завод для 3-й группы заводов = сумма среднегодовых стоимостей ОПФ
заводов в 3-й группе / число заводов в 3-й группе = 40,5/ 7 = 5,786 млн. руб.
Среднегодовая стоимость ОПФ в среднем
на один завод для 4-й группы заводов = сумма среднегодовых стоимостей ОПФ
заводов в 4-й группе / число заводов в 4-й группе = 35,2/ 5 = 7,04 млн. руб.
Среднегодовая стоимость ОПФ в среднем
на один завод для всей совокупности заводов = сумма среднегодовых стоимостей
ОПФ всех заводов / общее число заводов = 125,7/25 = 5,028 млн. руб.
3. Общая стоимость валовой продукции
1-й группы заводов (ОСВП1) = сумма стоимостей валовой продукции заводов в 1-й группе = 2,2 + 3,6 +3,6 + 3,4 = 12,8
млн. руб.
ОСВП2 = сумма стоимостей валовой
продукции заводов во 2-й группе = 4,4 +
5,9 + 5,9 + 4,7 +4,2 + 5,3 + 4,9 + 3,6 + 4,6 = 43,5 млн. руб.
ОСВП3 = сумма стоимостей валовой
продукции заводов в 3-й группе = 7,6 +
7,0 + 4,9 + 8,5 + 7,4 + 5,8 + 6,0 = 47,2 млн. руб.
ОСВП4 = сумма стоимостей валовой
продукции заводов в 4-й группе = 7,8 +
10,6 + 10,4 + 6,9 + 7,3 = 43 млн. руб.
Общая стоимость валовой продукции всех
заводов = сумма валовых стоимостей продукции всех заводов = ОСВП1 + ОСВП2 + ОСВП3 + ОСВП4 = 12,8 +
43,5 + 47,2 + 43 = 146,5 млн. руб.
Стоимость валовой продукции в среднем
на один завод для 1-й группы заводов = сумма стоимостей валовой продукции
заводов в 1-й группе / число заводов в
1-й группе = 12,8/4 = 3,2 млн. руб.
Стоимость валовой продукции в среднем
на один завод для 2-й группы заводов = сумма стоимостей валовой продукции
заводов во 2-й группе / число заводов в
группе = 43,5 / 9 = 4, 833 млн. руб.
Стоимость валовой продукции в среднем
на один завод для 3-й группы заводов = сумма стоимостей валовой продукции
заводов в 3-й группе / число заводов в
группе = 47,2/7 = 6,743 млн. руб.
Стоимость валовой продукции в среднем
на один завод для 4-й группы заводов = сумма стоимостей валовой продукции
заводов в 4-й группе / число заводов в
группе = 43/5 = 8,6 млн. руб.
Стоимость валовой продукции в среднем
на один завод по всей совокупности заводов = сумма стоимостей валовой продукции
всех заводов/ общее число заводов = 146,5/25 = 5,86 млн. руб.
4. Фондоотдача (Ф1) = общая
стоимость валовой продукции 1-й группы заводов/среднегодовую стоимость ОПФ в
среднем на один завод для 1-й группы = 12,8/2,95 = 4,334 руб. – размер валовой
продукции на рубль ОПФ.
Ф2 = 43,5/4,244 = 10,25
руб. – размер валовой продукции на рубль
ОПФ.
Ф3 = 47,2/5,786 = 8,158
руб. – размер валовой продукции на рубль
ОПФ.
Ф4 = 43/7,04 = 6,108 руб. –
размер валовой продукции на рубль ОПФ.
Общая
фондоотдача = общая стоимость валовой продукции всех заводов/среднегодовую
стоимость ОПФ в среднем на один завод = 146,5/5,028 = 29,137 руб.
Полученные
результаты представим в виде групповой таблицы:
Показатель
|
1-я группа
|
2-я группа
|
3-я группа
|
4-я группа
|
Вся совокупность заводов
|
|
Число
заводов
|
4
|
9
|
7
|
5
|
25
|
|
Общая
среднегодовая стоимость ОПФ
|
11,8
|
38,2
|
40,5
|
35,2
|
125,7
|
|
Среднегодовая
стоимость ОПФ на один завод
|
2,95
|
4,244
|
5,786
|
7,04
|
5,028
|
|
Общая
стоимость валовой продукции
|
12,8
|
43,5
|
47,2
|
43
|
146,5
|
|
Стоимость
валовой продукции в среднем на один завод
|
3,2
|
4,833
|
6,743
|
8,6
|
5,86
|
|
Фондоотдача
|
4,334
|
10,25
|
8,158
|
6,108
|
29,137
|
Задание 2
Имеются следующие данные по двум заводам,
вырабатывающим
однородную продукцию:
|
Номер завода
|
1989 г.
|
1990 г.
|
|
Затраты времени на единицу
продукции, ч.
|
Изготовлено продукции, шт.
|
Затраты времени на единицу
продукции, ч.
|
Затраты времени на всю
продукцию, ч.
|
|
1
2
|
4,0
7,0
|
540
320
|
4,9
3,8
|
380
840
|
Вычислите средние затраты времени ни изготовление
единицы продукции
по двум заводам в 1989 г. и
в 1990 г. Укажите, какой вид средней надо применить для вычисления этих
показателей.
Дайте характеристику динамики средних затрат
времени на изготовление
единицы продукции по
каждому заводу и по двум заводам вместе.
Решение
Рассчитаем средние затраты времени за 1989 год:
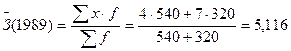ч. – средняя
арифметическая
взвешенная, где
x
– затраты времени на единицу продукции,
f
– изготовлено продукции.
Рассчитаем затраты времени за 1990 год:
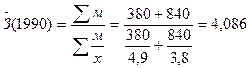ч. – средняя
гармоническая взвешенная, где м = хּf.
Характеристика
динамики средних затрат
|
Характеристика ряда динамики
|
По 1-му заводу
|
По 2-му заводу
|
По двум заводам вместе
|
|
Абсолютный прирост, Δ
|
0,9
|
-3,2
|
-1,03
|
|
Темп роста, Тр
|
122,5
|
54,29
|
79,87
|
|
Темп прироста, Тпр
|
22,5
|
-45,71
|
-20,13
|
Рассчитаем все показатели характеристики динамики
средних затрат для 1-
го завода:
Δ =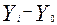 
= 4,9 – 4,0 =
0,9 ч. - затраты времени на единицу продукции
увеличились на 0,9 ч,
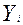- затраты времени на
единицу в 1990 г.
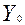- затраты времени на единицу в 1989 г.
Тр =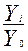 
ּ100% = 4,9/4,0ּ100% = 122,5 %
Тпр = Тр – 100 = 22,5 %
Затраты времени на единицу продукции увеличились на
0,9 ч
Рассчитаем все показатели характеристики динамики
средних затрат для 2-
го завода:
Δ = 3,8 – 7,0 = - 3,2 ч. затраты времени на
единицу продукции снизились на
3,2 ч.
Тр = 3,8/7,0 ּ100% = 54,29 %
Тпр = Тр – 100 = - 45,71 %.
Рассчитаем все показатели характеристики динамики
средних затрат по
двум заводам вместе:
Δ = 4,086 – 5,116 = -1,03 ч. -
затраты времени на единицу продукции снизились на 1,03 ч.
Тр =4,086/5,116 ּ100% = 79,87 %
Тпр = Тр – 100 = - 20,13 %
Задание 3
В результате 1%-ного бесповторного выборочного
обследования 100
работников предприятия
общественного питания треста столовых, отобранных в случайном порядке, получены
следующие данные о годовой выработке продукции:
|
Группы работников по
выработке продукции, тыс.руб.
|
Число работников, чел.
|
|
До 14
14-16
16-18
18-20
Свыше 20
|
5
20
35
25
15
|
|
Итого
|
100
|
На основе этих данных вычислите:
1. Среднюю выработку продукции на
одного человека.
2.
Средний квадрат отклонений (дисперсию) и среднее
квадратическое
отклонение.
3.
Коэффициент вариации.
4.
С вероятностью 0,954 предельную ошибку выборочной
средней и
возможные
границы, в которых ожидается среднегодовая выработка продукции работниками
треста столовых.
5. С вероятностью 0,954 предельную
ошибку выборочной доли и границы удельного веса работников треста столовых,
годовая выработка которых составляет от 14 до 20 тыс. руб.
Решение
1. Из таблицы видно, что величина
интервалов одинаковая и равняется единице, поэтому запишем в таблицу
центральные значения интервалов:
|
Группы работников по
выработке продукции, тыс.руб.
|
Центральное значение
интервала
|
Число работников, чел.
|
|
До 14
14-16
16-18
18-20
Свыше 20
|
13
15
17
19
21
|
5
20
35
25
15
|
|
Итого
|
85
|
100
|
1. 
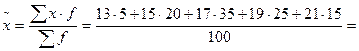17,5 тыс. руб.
2. Дисперсия равна:
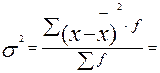
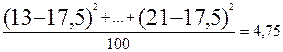тыс. руб.
Среднее квадратическое отклонение
равно:
= 
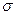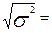2,179 тыс. руб.
3. Коэффициент вариации равен:
v = 
.
4. Объем
общей совокупности (N)
= 100ּ100 = 10000
чел.
n = 100 – объем выборочной
совокупности.
Средняя
ошибка выборочной средней равна:
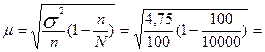0,217 тыс. руб.
Предельная
ошибка выборочной средней:
Δ = tּ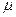
= 2 ּ 0,217 = 0,434 тыс.
руб., где
t – табличный коэффициент доверия при уровне вероятности 0,954.
Границы, в которых ожидается
среднегодовая выработка продукции:
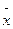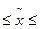
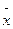- Δ 
+ Δ,
17,5 – 0,434 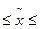17,5 + 0,434
17,066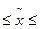17,934 – границы, в которых ожидается среднегодовая выработка
продукции.
5.
Средняя ошибка выборочной доли равна:
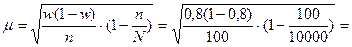0,04 тыс. руб. , где
w = (общая численность
работников с годовой выработкой от 14 до 20 тыс. руб.) / численность выборки =
(20 + 35 + 25)/100 = 0,8
Предельная
ошибка выборочной доли:
Δ = tּ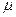 = 2 ּ 0,8
= 1,6 тыс. руб.
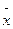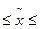
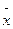- Δ + Δ,
17,5 – 1,6 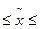17,5 + 1,6
15,9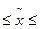19,1 – границы удельного веса работников с годовой выработкой
от 14 до 20 тыс. руб.
Задание 4
Производство телевизоров цветного
изображения в СССР характеризуется следующими данными:
Годы
|
Выпуск, млн. шт.
|
|
1980
1981
1982
1983
1984
1985
|
5,3
5,7
6,1
6,4
6,5
7,0
|
Для анализа динамики производства
телевизоров цветного изображения за 1980-1985 гг. вычислите:
1. Абсолютные приросты, темпы роста и
темпы прироста (по годам и к базисному 1980 г.), абсолютное содержание 1 %
прироста. Полученные показатели представьте в таблице.
2. Среднегодовое производство
телевизоров.
3. Среднегодовой темп роста и прироста
производства телевизоров.
Изобразите динамику производства
телевизоров на графике. Сделайте выводы.
Решение
1.
Характеристики ряда динамики представим в таблице:
|
Характеристика ряда
динамики
|
Базисный
|
Цепной
|
|
80
|
81
|
82
|
83
|
84
|
85
|
80
|
81
|
82
|
83
|
84
|
85
|
|
Абсолютный прирост, Δ
|
-
|
0,4
|
0,8
|
1,1
|
1,2
|
1,7
|
-
|
0,4
|
0,4
|
0,3
|
0,1
|
0,5
|
|
Темп роста, Тр
|
-
|
107,5
|
115,1
|
120,8
|
122,6
|
132,1
|
-
|
107,5
|
107
|
104,9
|
101,6
|
107,7
|
|
Темп прироста, Тпр
|
-
|
7,5
|
15,1
|
20,8
|
22,6
|
32,1
|
-
|
7,5
|
7
|
4,9
|
1,6
|
7,7
|
|
Абсолютное значение одного
% прироста, А
|
-
|
-
|
0,053
|
0,057
|
0,061
|
0,064
|
0,065
|
Рассчитаем базисные характеристики ряда
динамики:
Где 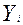- выпуск в i –м году
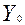- выпуск в 80-м году
Δ (81) = 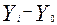= 5,7 – 5,3 = 0,4 млн. шт.
Δ (82) = 6,1 – 5,3 = 0,8 млн. шт.
Δ (83) = 6,4– 5,3 = 1,1 млн. шт.
Δ (84) = 6,5– 5,3 = 1,2 млн. шт.
Δ (85) = 7,0– 5,3 = 1,7 млн. шт.
Тр (81) = ּ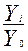100% = (5,7/5,3)ּ100% = 107,5 %
Тр (82) = (6,1/5,3)ּ100% = 115,1
%
Тр (83) = (6,4/5,3) ּ100% = 120,8
%
Тр (84) = (6,5/5,3) ּ100% = 122,6
%
Тр (85) = (7,0/5,3) ּ100% = 132,1
%
Тпр(81) = Тр – 100 = 107,5 – 100 = 7,5
%
Тпр(82) = Тр – 100 = 115,1 – 100 = 15,1
%
Тпр(83) = Тр – 100 = 120,8 – 100 = 20,8
%
Тпр(84) = Тр – 100 = 122,6 – 100 = 22,6
%
Тпр(85) = Тр – 100 = 132,1 – 100 = 32,1
%.
Рассчитаем цепные характеристики ряда
динамики:
Где 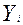- выпуск в i-м году
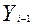- выпуск в i-1 году
Δ (81) =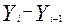 
= 5,7 – 5,3 = 0,4 млн. шт.
Δ (82) = 6,1 – 5,7 = 0,4 млн. шт.
Δ (83) = 6,4– 6,1 = 0,3 млн. шт.
Δ (84) = 6,5– 6,4 = 0,1 млн. шт.
Δ (85) = 7,0– 6,5 = 0,5 млн. шт.
Тр (81) = 
ּ100% = (5,7/5,3)ּ100% = 107,5 %
Тр (82) = (6,1/5,7)ּ100% = 107 %
Тр (83) = (6,4/6,1) ּ100% = 104,9
%
Тр (84) = (6,5/6,4) ּ100% = 101,6
%
Тр (85) = (7,0/6,5) ּ100% = 107,7
%
Тпр(81) = Тр – 100 = 107,5 – 100 = 7,5
%
Тпр(82) = Тр – 100 = 107 – 100 = 7 %
Тпр(83) = Тр – 100 = 104,9– 100 = 4,9 %
Тпр(84) = Тр – 100 = 101,6 – 100 = 1,6
%
Тпр(85) = Тр – 100 = 107,7– 100 = 7,7
%.
А (81) =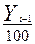 
= 5,3/100 = 0,053 млн.
шт.
А (82) = 5,7/100 = 0,057 млн. шт.
А (83) = 6,1/100 = 0,061 млн. шт.
А (84) = 6,4/100 = 0,064 млн. шт.
А (85) = 6,5/100 = 0,065 млн. шт.
2. Среднегодовое производство
телевизоров рассчитывается по формуле:
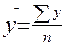= (5,3+5,7+6,1+6,4+6,5+7)/6 = 6,167 млн. шт., где
n – количество лет.
3. 
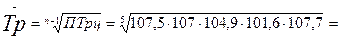105,7 %
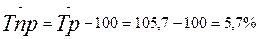
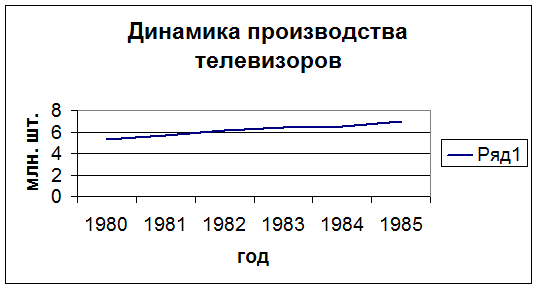
График
показывает постепенное увеличение выпуска телевизоров за рассматриваемый период
с 1980 по 1985 гг. Можно сказать, что и в последующие годы такая тенденция
сохраниться при фиксированных прочих факторах, влияющих на производство
телевизоров. В данном примере таким фактором является фактор времени. Резких
скачков и падений в производстве телевизоров за рассматриваемый период не
наблюдается.
Задание 5
Имеются
следующие данные о численности работников по участкам цеха:
|
Номер участка цеха
|
Число рабочих, чел.
|
|
на 1 января
|
на 1 февраля
|
на 1 марта
|
на 1 апреля
|
|
1
2
|
72
82
|
74
80
|
75
84
|
70
88
|
Вычислите среднесписочное число
работников за 1 квартал по каждому участку и по цеху в целом.
Поясните, почему методы расчета средних
уровней рядов динамики в заданиях 4 и 5 различны.
Решение
Рассчитаем среднесписочное число
работников за 1 квартал по 1-му участку, используя среднюю хронологическую
взвешенную:
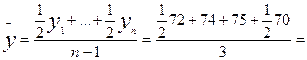73,333 чел.
Рассчитаем среднесписочное
число работников за 1 квартал по 2-му участку, используя среднюю
хронологическую взвешенную:
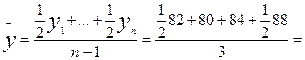83 чел.
Рассчитаем среднесписочное число
работников за 1 квартал по цеху в целом, используя среднюю хронологическую
взвешенную:
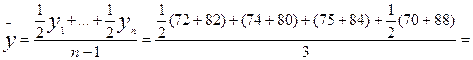156,333 чел.
В 4-м
задании исходные данные представляли собой полный интервальный ряд, уровни
интервального ряда динамики абсолютных величин характеризуют собой суммарный
итог какого-либо явления за определенный отрезок времени. Они зависят от
продолжительности этого периода времени, и поэтому их можно суммировать.
Поэтому для расчета средней в таких рядов используется средняя арифметическая
простая.
В 5-м задании уровни представляют собой
моментный полный ряд. Отдельные уровни такого ряда содержат элементы повторного
счета. Это делает бессмысленным суммирование уровней моментных рядов динамики,
поэтому для расчета средней используется средняя хронологическая простая.
Задание 6
Динамика себестоимости и объема
производства продукции характеризуется следующими данными:
|
Вид
продукции
|
Выработано
продукции, тыс. шт.
|
Себестоимость
единицы продукции, тыс. руб.
|
|
Базисный
период
|
Отчетный
период
|
Базисный
период
|
Отчетный
период
|
|
Завод
№ 1
АВ-35
ВП-40
Завод
№ 2
ВП-40
|
1250
2700
5000
|
1270
2500
5050
|
1,0
3,2
4,2
|
1,1
3,1
4,0
|
На основании имеющихся данных
вычислите:
1.
Для завода № 1 (по двум видам продукции вместе):
а) общий индекс затрат на производство
продукции.
б) общий индекс себестоимости
продукции.
в) общий индекс физического объема
производства продукции.
Определите в отчетном периоде изменение
суммы затрат на производство продукции и разложите по факторам (за счет
изменения себестоимости и объема выработанной продукции).
Покажите взаимосвязь между исчисленными
индексами.
2.
Для двух заводов вместе (по продукции ВП-40):
а) индекс себестоимости переменного
состава.
б) индекс стоимости постоянного
состава.
в) индекс влияния изменения структуры
производства продукции на динамику средней себестоимости.
Объясните разницу между величинами
индексов переменного и постоянного состава.
Решение
1.
Рассчитаем среднюю себестоимость единицы продукции в
базисном периоде:
а) Iз =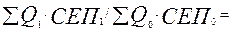 
(1270 ּ1,1+2500 ּ3,1)/(1250 ּ1+2700
ּ3,2) = 0,925.
б) IСЕП =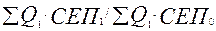 
=(1270 ּ1,1+2500 ּ3,1)/(1270 ּ1+2500
ּ3,2) = 0,987.
в) Iq =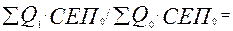 
(1270ּ1+2500 ּ3,2)/(1250 ּ
1+2700ּ3,2) = 0,937.
З = Q ּCЕП, З – затраты
Iз = Iq
ּ ICЕП = 0,937 ּ0,987 = 0,925 – снижение на
0,05, т.е 0,937 – 0,987.
Определим
долю влияния каждого фактора:
ΔЗ(Q) = (1270ּ1+2500 ּ3,2) -
(1250 ּ 1+2700ּ3,2) = - 620 тыс. руб.
ΔЗ(CЕП) = (1270 ּ1,1+2500 ּ3,1)
- (1270 ּ1+2500 ּ3,2) = - 123 тыс. руб.
Общее
изменение затрат:
ΔЗ = 91270
ּ1,1+2500 ּ3,1) - (1250 ּ1+2700 ּ3,2) = - 743 тыс. руб,
или (-123 + -620)
Таким
образом, в среднем по двум заводам сумма затрат в отчетном периоде снизилась по
сравнению с базисным на 743 тыс. руб., в том числе за счет изменения выработки
продукции она снизилась на 630 тыс. руб., а за счет изменения себестоимости
единицы продукции – на 123 тыс. руб. Изменение выработки продукции оказало
больше влияние на изменение суммы затрат, чем изменение себестоимости единицы
продукции.
2. а) Iпс =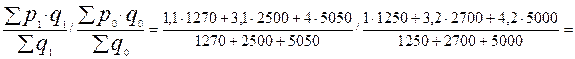 
0,964.
б) I псс =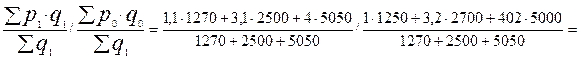 
0,950
в) Icтр = Iпс/ I псс = 0,964/0,95 = 1,015. За счет изменения структуры средняя
себестоимость продукции увеличилась на 1,5%.
Разница
индексов переменного и постоянного состава обуславливается тем, что количество
выработанной продукции в базисном и отчетном периоде неодинаково.
Задание 7
Имеются следующие данные о
товарообороте магазина потребительской кооперации:
|
Товарная
группа
|
Продано
товаров в фактических ценах, тыс. руб.
|
Индексы
цен в 1988 г. по сравнению с 1987 г.
|
|
1987
г.
|
1988
г.
|
|
Одежда
Трикотажные
изделия
Обувь
|
224,7
186,2
115,3
|
245,4
193,2
127,6
|
1,08
1,05
0,95
|
Вычислите:
1.
Общий индекс товарооборота в фактических ценах.
2.
Общий индекс физического объема продажи товаров.
3.
Общий индекс цен, используя взаимосвязь индексов.
Как повлияло изменение цен на величину
товарооборота в 1988 г.?
Решение
1.
Iqp =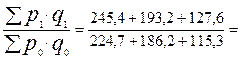 
1,034
2.
Iq =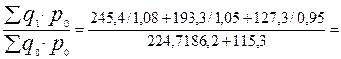 
1,038
3. Ip = Iqp / Iq = 1,034/1,038 = 0,997.
Товарооборот
1998 г. больше товарооборота 1987 г. на 3,4 % (или на
18,479 тыс. руб.: разность
числителя и знаменателя в индексе товарооборота)
Задание 8
Для изучения тесноты связи между
выпуском валовой продукции на один завод (результативный признак - У) и
оснащенностью заводов основными производственными фондами (факторный признак -
Х) по данным задания 1 вычислите коэффициент детерминации и эмпирическое
корреляционное отношение. Поясните их значение.
Решение
Эмпирическое
корреляционное отношение:
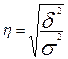, где
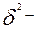межгрупповая дисперсия,
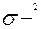общая дисперсия.
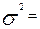
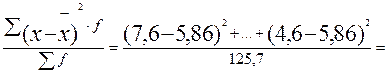4,518.
=
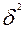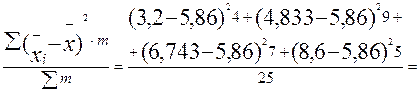3,232.
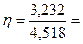0,715.
Эмпирическое корреляционное отношение характеризует тесноту связи между
взаимодействующими признаками. В данном примере, между выпуском валовой
продукции и оснащенностью производственными фондами имеется связь сильная,
равная 0,715.
Коэффициент детерминации равен:
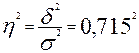= 0,511.
Коэффициент детерминации, равный 0,511,
означает, что 51,1% общей вариации выпуска валовой продукции объясняется
оснащенностью производственных фондов, и, соответственно, 48,9% вариации –
всеми прочими факторами, неучтенными в данной группировке.
Список
использованной литературы
1) Елисеева И.И., Юзбашев М.М. Общая
теория статистики: Учебник. – М.: Финансы и статистика, 1999. – 368 с.
2) Ефимова М.Р., Петрова Е.В., Румянцев
В.Н. Общая теория статистики: Учебник. – М.: ИНФРА-М, 2000. – 416 с.
3) Шмойлова Р.А. Теория статистики:
Учебник. – М.: Финансы и статистика, 2001. – 560 с.