Содержание
Введение. 2
1. Теоретическая
часть. 3
1.1 Метод
выборочных наблюдений. 3
1.1.1
Выборочное исследование. 3
1.1.2.
Ошибка выборочной средней. 7
1.1.3
Ошибка выборочной доли. 14
2. Практическая
часть. 19
3.Аналитическая
часть. 33
3.1 Постановка задачи. 33
3.1.2.Методика решения задачи. 34
3.1.3.Технология выполнения компьютерных расчетов. 35
3.1.4. Анализ статистических расчетов. 37
Заключение. 38
Литература. 40
Приложение 1. 42
Введение
Процесс образования выборки называется отбором, который осуществляется в
порядке беспристрастного, случайного отбора единиц из генеральной совокупности.
Основным условием проведения выборочного наблюдения является предупреждение
возникновения систематических (тенденциозных) ошибок, возникающих вследствие
нарушения принципа равных возможностей попадания в выборку каждой единицы
совокупности. Предупреждение систематических ошибок достигается в результате
применения научно обоснованных способов формирования выборочной совокупности.
Существуют различные способы отбора: индивидуальный, групповой (серийный),
комбинированный, повторный (возвратный),
бесповторный (безвозвратный),одноступенчатый, многоступенчатый,
собственно–случайный, механический, типический, двухфазный и многофазный отбор.
Цель данной работы раскрыть понятие и сущность выборочного
метода статистического исследования.
Задача: на основе
изученного теоретического материала рассчитать практически группировку, связь
между признаками, определить ошибку выборки и ошибку выборки доли, показать на
конкретном примере аналитические расчеты с употреблением прикладной программы Excel.
1. Теоретическая
часть
1.1 Метод выборочных наблюдений
1.1.1 Выборочное
исследование
При индивидуальном отборе в
выборку отбираются отдельные единицы совокупности. Отбор повторяется столько
раз, сколько необходимо отобрать единиц.
Групповой (серийный) отбор заключается
в отборе серий (например, отбор изделий для проверки их целыми партиями). Если
обследованию подвергаются все единицы отобранных серий, отбор называется серийным, а если обследуется только
часть единиц каждой серии, отбираемых в индивидуальным порядке из серии, то – комбинированным.
Если в процессе отбора отобранная единица не исключается из совокупности,
т.е. возвращается в совокупность, и может быть повторно отобранной, то такой
отбор называется повторным или возвратным, в противном случае – бесповторным или безвозвратным. Серийный отбор, как правило, безвозвратный.
При повторном отборе вероятность попадания в выборочную совокупность
всех единиц генеральной совокупности остается одинаковой. При бесповторном -
для оставшихся единиц совокупности вероятность попадания в выборку
увеличивается.
При одноступенчатом
отбираются единицы совокупности (или серии) непосредственно для наблюдения. При
многоступенчатом отбираются сначала
крупные серии единиц (первая ступень отбора), наблюдению они не подвергаются.
Затем из них отбираются серии, меньшие по численности единиц (вторая ступень),
наблюдению не подвергаются, и так до тех пор, пока не будут отобраны те единицы
совокупности (серии), которые будут подвергнуты наблюдению.
Собственно–случайный отбор
состоит в отборе единиц (серий) из всей генеральной совокупности в целом
посредством жеребьевки или на основании таблиц случайных чисел.
Жеребьевка состоит в том, что на каждую единицу отбора составляется карточка,
которой присуждается порядковый номер. После тщательного перемешивания по
очереди извлекаются карточки, пока не будет отобрано требуемое число единиц.
Случайными числами называются ряды чисел, являющихся реализациями
последовательности взаимно независимых и одинаково распределенных случайных
величин. Эти последовательности чисел получаются либо с помощью физических
генераторов (подбрасывание кубиков с нанесенными на их сторонами цифрами;
вытягиванием из урны карточек с написанными на них цифрами, преобразование
случайных сигналов и др. физико–технические процессы), либо с помощью
программных генераторов (аналитическим методом с помощью программ для ЭВМ).
Числа, являющиеся результатами соответствующей вычислительной процедуры,
называются псевдослучайными числами. Последовательность псевдослучайных чисел
носит детерминированный характер, но в определенных границах она удовлетворяет
свойствам равномерного распределения и свойству случайности.
Случайные числа могут быть выбраны по
таблице случайных чисел (приложение 1), которая содержит 2000 случайных чисел,
объединенных для удобства пользования таблицей в 500 блоков по 4 значения)
Например,
5489, 5583, 3156, 0835, 1988, 3912.
Применение комбинаций этих цифр зависит
от размера совокупности: если в генеральной совокупности 1000 единиц, то
порядковый номер каждой единицы должен состоять из двух цифр от 000 до 999. В
этом случае первые 8 номеров единиц выборочной совокупности следующие:
548, 955, 833, 156, 083, 519, 883,
912.
При произвольном объеме генеральной
совокупности, отличающегося от 100, 1000, 10000 могут использоваться
псевдослучайные числа, сформированные на ЭВМ, или из таблицы случайных чисел
формируется последовательность случайных величин, распределенных в интервале от
0 до 1. Например, в приведенном выше примере
0,5489; 0,5583; 0,3156; 0,0835;
0,1988; 0,3912 и т.д.
Если генеральная совокупность состоит
из 2000 единиц, то в выборочную совокупность должны войти единицы с номерами:
2000 × 0,5489 = 1097,8 или 1099;
2000 × 0,5583 = 1116,6 или 1117;
2000 × 0,3156 = 631,2 или
631;
2000 × 0,0835 = 167,0 или
167;
2000 × 0,1988 = 397,6 или
398;
2000 × 0,3912 = 782,4 или
782.
Процесс формирования случайных чисел и
определения номера отбираемой единицы продолжается до тех пор, пока не будет
получен заданный объем выборочной совокупности.
Можно предложить другой способ
случайного отбора единиц в выборку. Допустим, что выборка состоит из 75 единиц, а генеральная
совокупность - из 780. Из таблицы случайных чисел выбираются, например,
следующие
5489, 5583, 3156, 0835, 1988, 3912.
В выборку могут войти только единицы,
порядковые номера которых равны трехзначным числам меньше 780. Поэтому,
используя только три последние цифры каждого числа, отбирается необходимые 75
номеров: 489, 583, 156 и т.д. Можно использовать и первые три цифры каждого
числа, тогда отобранные номера: 548, 558, 315, 83, 198, 391. Можно разбить
случайные четырехзначные случайные числа на ряд, состоящий из трехзначных чисел:
548, 955, 833, 156, 083, 519, 883,
912
и отобрать из них номера, которые
меньше 780, а именно: 548, 156, 83, 519.
Механический отбор
заключается в том, что составляется список единиц генеральной совокупности и в
зависимости от числа отбираемых единиц (серий) устанавливается шаг отбора, т.е.
через какой интервал следует брать для наблюдения единицы (серии). Например, в
простейшем случае, при 10%–м отборе,
отбирается каждая десятая единица по этому списку, т.е. если первой взята
единица за № 1, то следующими отбираются 11–я, 21–я и т.д. В такой
последовательности производится отбор, если единицы совокупности расположены в
списке без учета их “рангов”, т.е. значимости по изучаемым признакам. Начало
отбора в этом случае не имеет значения, его можно начать в приведенном примере
от любой единицы из первого десятка. При расположении единиц совокупности в
ранжированном порядке за начало отбора должна быть принята середина интервала
(шага отбора) во избежание систематической ошибки выборки.
При достаточно большой совокупности этот способ отбора близок к
собственно случайному, при условии, что применяемый список не составлен таким
образом, чтобы какие-то единицы совокупности имели больше шансов попасть в
выборку.
При типическом отборе
генеральная совокупность разбивается на типические группы единиц по какому–либо
признаку (формируются однородные совокупности), а затем из каждой из них
производится механический или собственно–случайный отбор. Отбор единиц из типов
производится тремя методами: пропорционально численности единиц типических
групп, непропорционально численности единиц типических групп и пропорционально
колеблемости признака в группах.
В целях экономии средств данные по
некоторым интересующим исследователя признакам можно анализировать на основании
изучения всех единиц выборочной совокупности, а по другим признакам - на
основании части единиц выборочной совокупности, которые представляют подвыборку
из единиц первоначальной выборки. Этот метод называется двухфазным отбором. При наличии нескольких подвыборок - метод многофазного отбора.
Многофазный отбор по своей структуре
отличается от многоступенчатого отбора, так при многофазном отборе используются
на каждой фазе одни и те же отобранные единицы, при многоступенчатом отборе на
разных ступенях применяются единицы отбора разных порядков. Многофазным отбором
чаще всего пользуются в тех случаях, когда различно число единиц, необходимых
для определения отдельных показателей с заданной точностью. Это связано как с
различиями в степени колеблемости признаков, так и с разной точностью,
требуемой для расчетов. Ошибки при многофазной выборке рассчитываются на каждой
фазе отдельно.
1.1.2. Ошибка выборочной
средней
Ошибка выборочной средней представляет собой расхождение (разность)
между выборочной средней 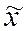 и генеральной
средней
и генеральной
средней 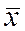 , возникающее вследствие несплошного выборочного характера
наблюдения. Величина ошибки выборочной средней определяется как предел
отклонения
, возникающее вследствие несплошного выборочного характера
наблюдения. Величина ошибки выборочной средней определяется как предел
отклонения 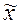 от
от 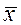 , гарантируемый с заданной вероятностью:
, гарантируемый с заданной вероятностью:
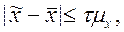
где
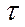 – гарантийный коэффициент, зависящий от
вероятности
– гарантийный коэффициент, зависящий от
вероятности 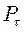 , с которой гарантируется невыход
разности
, с которой гарантируется невыход
разности 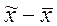 за пределы
за пределы 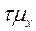 ;
; 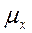 – средняя ошибка
выборочной средней.
– средняя ошибка
выборочной средней.
Значения гарантийного коэффициента 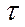 и соответствующие им
вероятности
и соответствующие им
вероятности 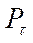 приведены в табл.4.1. Обычно вероятность
принимается равной 0,9545 или 0,9973, а
приведены в табл.4.1. Обычно вероятность
принимается равной 0,9545 или 0,9973, а
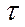 при этом равно
соответственно 2 и 3.
при этом равно
соответственно 2 и 3.
Таблица 1.1
Значения гарантийного
коэффициента 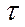
|
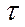
|
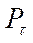
|
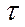
|
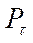
|
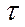
|
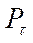
|
|
1,00
1,10
1,20
1,30
1,40
1,50
1,60
|
0,6827
0,7287
0,7699
0,8064
0,8385
0,8664
0,8904
|
1,70
1,80
1,90
2,00
2,10
2,20
2,30
|
0,9109
0,9281
0,9426
0,9545
0,9643
0,9722
0,9786
|
2,40
2,50
2,60
2,70
2,80
2,90
3,00
|
0,9836
0,9876
0,9907
0,9931
0,9949
0,9963
0,9973
|
Источник: Н.В.Смирнов,
И.В.Дунин-Барковский. Курс теории вероятностей и математической статистики для
технических приложений. - М.: Наука, 1965. 512 с.
Стр.173
Средняя ошибка определяется как среднее квадратическое отклонение
средней величины в генеральной совокупности (средней генеральной)

В математической статистике
доказывается, что величина средней квадратической стандартной ошибки простой
случайной повторной выборки может быть определена по формуле
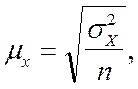
где
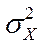 - дисперсия признака в генеральной совокупности.
- дисперсия признака в генеральной совокупности.
Дисперсия суммы независимых величин равна сумме дисперсий слагаемых
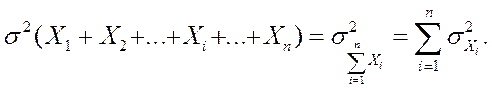
Если все величины Xi имеют одинаковую дисперсию, то
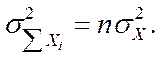
Тогда дисперсия средней
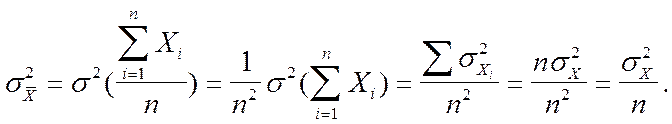 Тогда средняя
ошибка при определении средней
Тогда средняя
ошибка при определении средней
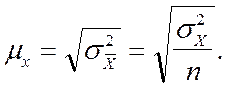
Между дисперсиями в генеральной и
выборочной совокупностях существует следующее соотношение:
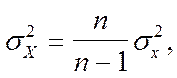
где
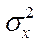 – дисперсия признака в выборке.
– дисперсия признака в выборке.
Если n достаточно велико, то 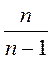 близко к единице и
дисперсию в генеральной совокупности можно заменить на дисперсию в выборке.
близко к единице и
дисперсию в генеральной совокупности можно заменить на дисперсию в выборке.
Тогда средняя ошибка средней в генеральной совокупности может быть как
среднее квадратическое отклонение средней величины в выборочной совокупности
(средней выборочной)
Средняя ошибка выборочной средней
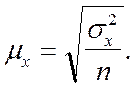
Значения средней ошибки выборки определяются по формуле
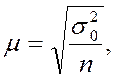
где
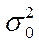 – дисперсия в
генеральной совокупности.
– дисперсия в
генеральной совокупности.
Между дисперсиями в генеральной и
выборочной совокупностях существует следующее соотношение:
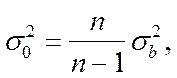
где
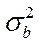 – дисперсия в выборке.
– дисперсия в выборке.
Если n достаточно велико, то 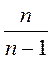 близко к единице и
дисперсию в генеральной совокупности можно заменить на дисперсию в выборке.
близко к единице и
дисперсию в генеральной совокупности можно заменить на дисперсию в выборке.
При повторном отборе средняя ошибка определяется следующим образом:
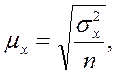
где
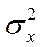 – средняя величина
дисперсии количественного признака
– средняя величина
дисперсии количественного признака 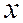 , которая рассчитывается по формуле средней арифметической
невзвешенной
, которая рассчитывается по формуле средней арифметической
невзвешенной
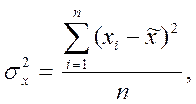
или средней арифметической взвешенной
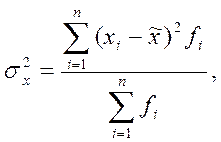
где fi
– статистический вес.
Формулы расчета средней ошибки
выборочной средней для различных, наиболее часто используемых способов отбора
выборочной совокупности приведены в табл.2.1
Таблица 2.1
Формулы расчета средних ошибок
выборочной доли
и выборочной средней
Метод отбора выборки
|
Средняя ошибка
|
|
выборочной доли
|
выборочной средней
|
Механический или собственно–случайный
повторный отбор
|
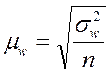
|
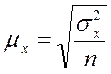
|
Механический или собственно–случайный
бесповторный отбор
|
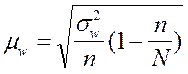
|
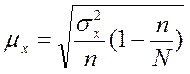
|
|
Серийный отбор при повторном
отборе равновеликих серий
|
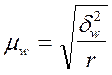
|
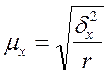
|
Серийный отбор при бесповторном
отборе равновеликих серий
|
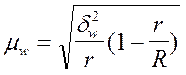
|
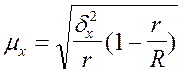
|
Типический отбор при повторном
случайном отборе внутри групп, пропорциональном объему групп
|
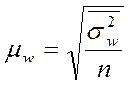
|
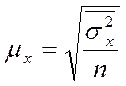
|
|
Типический отбор при бесповторном
случайном отборе внутри групп, пропорциональном объему групп
|
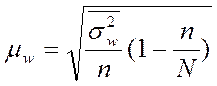
|
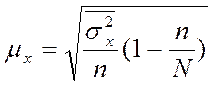
|
где N – численность генеральной совокупности;
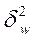 – межсерийная
дисперсия выборочной доли;
– межсерийная
дисперсия выборочной доли;
r – число отобранных серий;
R – число серий в
генеральной совокупности;
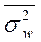 – средняя из
групповых дисперсий выборочной доли;
– средняя из
групповых дисперсий выборочной доли;
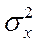 – дисперсия
признака x в выборке;
– дисперсия
признака x в выборке;
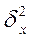 – межсерийная
дисперсия выборочных средних;
– межсерийная
дисперсия выборочных средних;
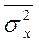 – средняя из
групповых дисперсий выборочной средней.
– средняя из
групповых дисперсий выборочной средней.
При
бесповторном оборе с каждой отобранной единицей или серией вероятность отбора
оставшихся единиц или серий повышается, при этом средняя ошибка выборочной
средней уменьшается по сравнению с повторным отбором и имеет следующий вид:
для механического или собственно
случайного бесповторного отбора
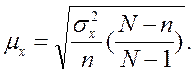
При достаточно большом объеме
совокупности N можно воспользоваться формулой
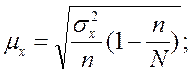
для серийного бесповторного отбора
равновеликих серий
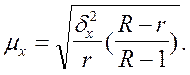
При достаточно большом числе серий в генеральной совокупности R можно воспользоваться
формулой
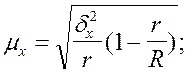
для типического отбора с бесповторным
случайном отборе внутри групп, пропорциональном объему групп
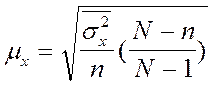
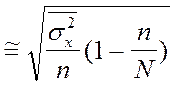 .
.
Межсерийная дисперсия выборочных средних
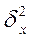 и средняя из выборочных
дисперсий типических групп
и средняя из выборочных
дисперсий типических групп 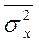 вычисляются следующим
образом:
вычисляются следующим
образом:
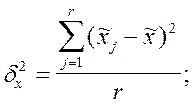
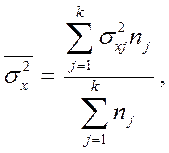
где
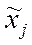 – среднее значение
показателя в j – й серии;
– среднее значение
показателя в j – й серии;
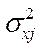 – дисперсия
признака x в j – й типической группе;
– дисперсия
признака x в j – й типической группе;
nj – число единиц в j
–й типической группе.
1.1.3 Ошибка выборочной
доли
Выборочная доля представляет
собой отношение числа единиц, обладающих данным признаком или данным его
значением ( m ) к общему числу единиц выборочной совокупности ( n )
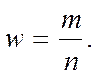
(Эту статистическую характеристику не
следует путать с долей выборки, являющейся отношением числа единиц выборочной
совокупности к числу единиц генеральной совокупности).
Ошибка выборочной доли
представляет собой расхождение (разность) между долей в выборочной
совокупности ( w ) и долей в генеральной совокупности ( p ),
возникающее вследствие несплошного характера наблюдения. Величина ошибки
выборочной доли определяется как предел отклонения w от p , гарантируемый с заданной вероятностью:
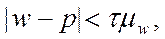
где
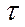 – гарантийный коэффициент, зависящий от вероятности
– гарантийный коэффициент, зависящий от вероятности 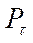 , с которой гарантируется невыход
разности w –p за пределы
, с которой гарантируется невыход
разности w –p за пределы 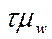 ;
; 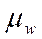 – средняя ошибка выборочной
доли.
– средняя ошибка выборочной
доли.
Средняя ошибка выборочной доли
определяется по формуле
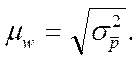
Или, как было доказано выше,
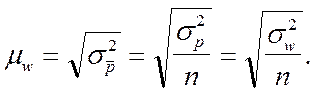
где 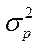 – дисперсия доли в генеральной совокупности
(дисперсия генеральной доли);
– дисперсия доли в генеральной совокупности
(дисперсия генеральной доли);
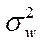 – дисперсия доли в
выборке (дисперсия выборочной доли).
– дисперсия доли в
выборке (дисперсия выборочной доли).
Приведенная формула средней ошибки
выборочной доли применяется при повторном отборе.
Для определения дисперсии альтернативного признака допустим, что общее
число единиц совокупности равно n
. Число единиц, обладающих данным признаком - f
, тогда число единиц, не
обладающих данным признаком, равно n-f . Ряд
распределения качественного (альтернативного) признака
|
Значение переменной
|
Частота повторений
|
|
1
0
|
f
n-f
|
|
Итого
|
n
|
Средняя арифметическая такого ряда
равна:
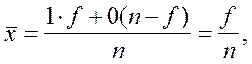
то есть равна относительной частоте
(частости) появления данного признака, которую можно обозначить через p
, тогда 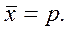
Таким образом, доля единиц, обладающих
данным признаком равна p ; соответственно доля единиц, не
обладающих данным признаком, равна q ; p+q =1. Тогда дисперсия альтернативного признака
определяется по формуле
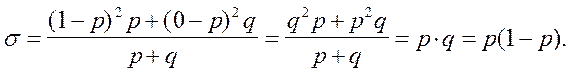
Для показателя доли альтернативного признака в выборке (выборочной доли)
дисперсия определяется по формуле
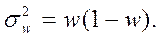
При бесповторном отборе численность
генеральной совокупности сокращается, поэтому дисперсия умножается на
коэффициент 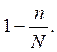 Формулы расчета
средних ошибок выборочной доли для различных способов отбора единиц из
генеральной совокупности приведены в табл. 1,2;1,3 и 4
Формулы расчета
средних ошибок выборочной доли для различных способов отбора единиц из
генеральной совокупности приведены в табл. 1,2;1,3 и 4
Дисперсии в формулах расчета средних ошибок выборочной доли в табл.4.2.
рассчитываются следующим образом:
– межсерийная дисперсия выборочной доли
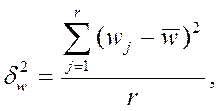
где
wj – выборочная доля в j –й серии;
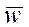 – средняя величина доли во всех сериях;
– средняя величина доли во всех сериях;
– средняя из групповых дисперсий
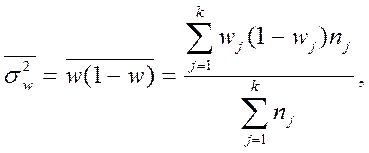
где wj
– выборочная доля в j –й
типической группе;
nj –
число единиц в j –й
типической группе;
k
– число типических групп.
Для случая, когда доля (частость) даже
приблизительно неизвестна, можно произвести "грубый" расчет средней
ошибки выборки для доли, используя в расчете максимальную величину дисперсии
доли, равную 0,25. Тогда для повторного отбора
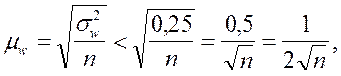
бесповторного отбора
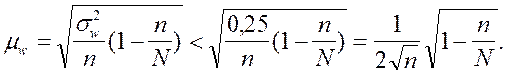
Предельное значение ошибки выборочной доли определяется по следующей
формуле:
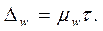
Величина средней ошибки выборочной
доли 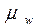 зависит от доли изучаемого признака в генеральной
совокупности, числа наблюдений и способа отбора единиц из генеральной
совокупности для наблюдения, а величина предельной ошибки
зависит от доли изучаемого признака в генеральной
совокупности, числа наблюдений и способа отбора единиц из генеральной
совокупности для наблюдения, а величина предельной ошибки 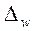 зависит еще и от
величины вероятности
зависит еще и от
величины вероятности 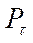 , с
которой гарантируются результаты выборочного наблюдения.
, с
которой гарантируются результаты выборочного наблюдения.
Распространение выборочных данных на генеральную совокупность производится
с учетом доверительных интервалов. Доля альтернативного признака в генеральной
совокупности равна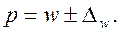
2. Практическая часть
1.
Определить
рентабельность продукции и сделать группировку по признаку. Число групп пять.
Таблица 1.
|
№ п/п
|
Выручка от
продажи продукции
|
Затраты на
производство и
реализацию
продукции, Х
|
Рентабельность
продукции, У
|
|
1
|
36,45
|
30,255
|
20,4760
|
|
2
|
23,4
|
20,124
|
16,2791
|
|
3
|
46,54
|
38,163
|
21,9506
|
|
4
|
59,752
|
47,204
|
26,5825
|
|
5
|
41,415
|
33,546
|
23,4573
|
|
6
|
26,86
|
22,831
|
17,6471
|
|
7
|
79,2
|
60,984
|
29,8701
|
|
8
|
54,72
|
43,776
|
25,0000
|
|
9
|
40,424
|
33,148
|
21,9500
|
|
10
|
30,21
|
25,376
|
19,0495
|
|
11
|
42,418
|
34,359
|
23,4553
|
|
12
|
64,575
|
51,014
|
26,5829
|
|
13
|
51,612
|
41,806
|
23,4560
|
|
14
|
35,42
|
29,753
|
19,0468
|
|
15
|
14,4
|
12,528
|
14,9425
|
|
16
|
36,936
|
31,026
|
19,0485
|
|
17
|
53,392
|
42,714
|
24,9988
|
|
18
|
41
|
33,62
|
21,9512
|
|
19
|
55,68
|
43,987
|
26,5829
|
|
20
|
18,2
|
15,652
|
16,2791
|
|
21
|
31,8
|
26,394
|
20,4819
|
|
22
|
39,204
|
32,539
|
20,4831
|
|
23
|
57,128
|
45,702
|
25,0011
|
|
24
|
28,44
|
23,89
|
19,0456
|
|
25
|
43,344
|
35,542
|
21,9515
|
|
26
|
70,72
|
54,454
|
29,8711
|
|
27
|
41,832
|
34,302
|
21,9521
|
|
28
|
69,345
|
54,089
|
28,2054
|
|
29
|
35,903
|
30,159
|
19,0457
|
|
30
|
50,22
|
40,678
|
23,4574
|
|
Σ
|
|
1069,615
|
668,101067
|
|
В
среднем
|
|
35,6538
|
22,27
|
Интервал между группами 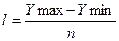
Где l-интервал между группами,
Y min-минимальное значение,
Y max-максимальное значение
n-число групп
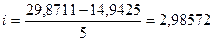
|
число
предприятий
|
число
предприятий f
|
Середина
интервала Х
|
xf
|
|
от
14,9425-17,92822
|
4
|
16,43
|
65,72
|
|
от
17,92822-20,91394
|
6
|
19,41
|
116,46
|
|
от
20,91394-23,89966
|
8
|
22,4
|
179,2
|
|
от
23,89966-26,88538
|
6
|
25,38
|
152,28
|
|
от
26,88538-29,8711
|
6
|
28,37
|
170,22
|
|
Итого
|
30
|
|
683,88
|
|
Х сред
|
|
|
22,94
|
Мода М0 – значение
случайной величины, встречающейся с наибольшей вероятностью в вариационном
ряду.
В интервальных рядах
распределения с равным интервалом мода вычисляется по формуле:
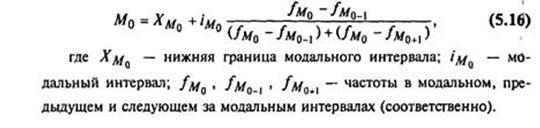
в нашем случае, это:
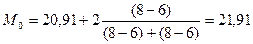
Итак, модальным значением
рентабельности предприятий является рентабельность равная 21, 91 %
Медиана Ме- это вариант,
который находиться в середине вариационного ряда. Вычисляется по формуле:

Прежде всего найдем
медианный интервал, таким интервалом, очевидно будет рентабельность продукции
(23,91 -23,89), поскольку его кумулятивная частота равна 18 (8=6+4), что
превышает половину суммы всех частот (30:2=15). Нижняя граница интервала 20,91,
его частота 8; частота, накопленная до него равна 6.
Подставив данные в
формулу, найдем значение медиан, %.
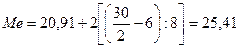
Полученный результат
говорит о том, что из 30 предприятий региона
24 имеют рентабельность продукции менее 25,4%, а 6 более 25,4%
Средняя арифметическая.
После того, как найдены середины интервалов, вычисления делают также, как и в
дискретном ряду, - варианты умножают на частоты и сумму произведений делят на
сумму частот, %.
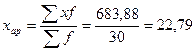
Итак, средний процент
рентабельности продукции 22,79 %.
Коэффициент вариации представляет
собой выраженное в процентах отношение
среднего квадратического отклонения к средней арифметической:
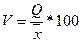
Коэффициент вариации
используют не только для сравнительной оценки вариации единиц совокупности, но
и как характеристику однородности совокупности. Совокупность считается
количественно однородной, если коэффициент вариации не превышает 33%.
Покажем это на нашем
примере. Для этого составим таблицу с необходимыми вычислениями
|
число предприятий
|
число предприятий f
|
Середина
интервала Х
|
xf
|
(х-х)
|
(х-х)2
|
(х-х)2f
|
|
от
14,9425-17,92822
|
4
|
16,43
|
65,72
|
- 6,37
|
40,57
|
162,28
|
|
от
17,92822-20,91394
|
6
|
19,41
|
116,46
|
- 3, 37
|
11,35
|
68,1
|
|
от
20,91394-23,89966
|
8
|
22,4
|
179,2
|
- 0,4
|
0,16
|
1,28
|
|
от
23,89966-26,88538
|
6
|
25,38
|
152,28
|
2,58
|
6,65
|
39,9
|
|
от 26,88538-29,8711
|
6
|
28,37
|
170,22
|
5,57
|
31,02
|
33,42
|
|
Итого
|
30
|
|
683,88
|
|
|
304,98
|
|
Х сред
|
|
|
22,94
|
|
|
|
Найдем среднюю
рентабельности
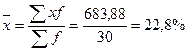
рассчитаем дисперсию
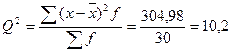
Найдем среднее
квадратическое отклонение
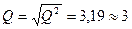
Определим коэффициент
вариации, %
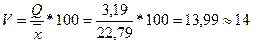
Таким образом
рентабельность довольна однородна, т.к. не превышает 33%
2.
Определить
связь между признаками
Для определения связи
между признаками используем коэффициент корреляции, применяемого для
определения взаимосвязи между двумя количественными переменными. Этот
коэффициент определяется по формуле:
r = 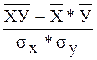
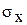 =
= 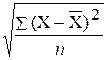
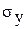 =
= 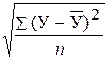
Для расчета этих
показателей составим сначала таблицу следующего вида, где осуществим
предварительные расчеты необходимых величин:
Таблица 3.
|
№ п/п
|
Выручка
от продажи продукции
|
Затраты на
производство и
реализацию
продукции, Х
|
Рентабельность
продукции, У
|
У²
|
X²
|
У
· X
|
|
1
|
36,45
|
30,255
|
20,4760
|
419,26
|
915,37
|
619,5
|
|
2
|
23,4
|
20,124
|
16,2791
|
265,01
|
404,98
|
327,6
|
|
3
|
46,54
|
38,163
|
21,9506
|
481,83
|
1456,4
|
837,7
|
|
4
|
59,752
|
47,204
|
26,5825
|
706,63
|
2228,2
|
1254,8
|
|
5
|
41,415
|
33,546
|
23,4573
|
550,25
|
1125,3
|
786,9
|
|
6
|
26,86
|
22,831
|
17,6471
|
311,42
|
521,25
|
402,9
|
|
7
|
79,2
|
60,984
|
29,8701
|
892,22
|
3719
|
1821,6
|
|
8
|
54,72
|
43,776
|
25,0000
|
625
|
1916,3
|
1094,4
|
|
9
|
40,424
|
33,148
|
21,9500
|
481,8
|
1098,8
|
727,6
|
|
10
|
30,21
|
25,376
|
19,0495
|
362,88
|
643,94
|
483,4
|
|
11
|
42,418
|
34,359
|
23,4553
|
550,15
|
1180,5
|
805,9
|
|
12
|
64,575
|
51,014
|
26,5829
|
706,65
|
2602,4
|
1356,1
|
|
13
|
51,612
|
41,806
|
23,4560
|
550,18
|
1747,7
|
980,6
|
|
14
|
35,42
|
29,753
|
19,0468
|
362,78
|
885,24
|
566,7
|
|
15
|
14,4
|
12,528
|
14,9425
|
223,28
|
156,95
|
187,2
|
|
16
|
36,936
|
31,026
|
19,0485
|
362,85
|
962,61
|
591
|
|
17
|
53,392
|
42,714
|
24,9988
|
624,94
|
1824,5
|
1067,8
|
|
18
|
41
|
33,62
|
21,9512
|
481,86
|
1130,3
|
738
|
|
19
|
55,68
|
43,987
|
26,5829
|
706,65
|
1934,9
|
1169,3
|
|
20
|
18,2
|
15,652
|
16,2791
|
265,01
|
244,99
|
254,8
|
|
21
|
31,8
|
26,394
|
20,4819
|
419,51
|
696,64
|
540,6
|
|
22
|
39,204
|
32,539
|
20,4831
|
419,56
|
1058,8
|
666,5
|
|
23
|
57,128
|
45,702
|
25,0011
|
625,05
|
2088,7
|
1142,6
|
|
24
|
28,44
|
23,89
|
19,0456
|
362,74
|
570,73
|
455
|
|
25
|
43,344
|
35,542
|
21,9515
|
481,87
|
1263,2
|
780,2
|
|
26
|
70,72
|
54,454
|
29,8711
|
892,28
|
2965,2
|
1626,6
|
|
27
|
41,832
|
34,302
|
21,9521
|
481,89
|
1176,6
|
753
|
|
28
|
69,345
|
54,089
|
28,2054
|
795,54
|
2925,6
|
1525,6
|
|
29
|
35,903
|
30,159
|
19,0457
|
362,74
|
909,57
|
574,4
|
|
30
|
50,22
|
40,678
|
23,4574
|
550,25
|
1654,7
|
954,2
|
|
Σ
|
|
1069,615
|
668,101067
|
15322
|
42010
|
25092,5
|
|
В
среднем
|
|
35,6538
|
22,27
|
|
|
836,42
|
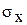 =
= 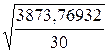 =11,36335
=11,36335
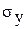 =
= 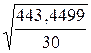 = 3,8447
= 3,8447
r = 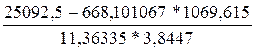 = 0,9706
= 0,9706
По таблице 4 определяем, что взаимосвязь между
рассматриваемыми признаками является
сильной.
Таблица 4 - Сила связи в зависимости от величины
коэффициента корреляции
|
Коэффициент
корреляции
|
Сила
связи
|
|
От +
0,81 до ± 1,00
|
Сильная
|
|
От +
0,61 до ± 0,80
|
Умеренная
|
|
От ±
0,41 до ± 0,60
|
Слабая
|
|
От ±
0,21 до ± 0,40
|
Очень
слабая
|
|
От +
0,00 до ± 0,20
|
Отсутствует
|
Оценка степени тесноты связи с помощью
коэффициента корреляции проводится, как правило, на основе
более или менее ограниченной информации об изучаемых явлениях.
В этой связи возникает вопрос, насколько правомерно заключение о наличии
корреляционной связи в той генеральной совокупности, из которой была произведена
выборка. Для ответа на него необходимо оценить существенность линейного
коэффициента корреляции, дающую возможность распространить выводы по результатам
выборки на генеральную совокупность.
Для малого объема выборочной совокупности используется критерий
Стьюдента:
t расч
= 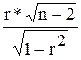 ,
,
где п — объем выборки.
Произведем оценку существенности
коэффициента корреляции между относительным объемом продаж и относительным
уровнем затрат на рекламу. Поскольку объем выборки в нашем случае
незначительный, то для расчета используем критерий Стьюдента:
tрасч
= 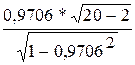 = 17,108
= 17,108
Полученную величину tрасч
сравнивают с табличным
значением t-критерия Стьюдента
(число степеней свободы равно n —
2). Если расчетная величина превосходит табличное значение, то связь
между признаками подтверждается.
Из таблицы распределения
Стьюдента находим tα = 2,878
(для чиcла степеней
свободы n– 2=18 и уровня значимости 0,01).
Величина tрасч превышает табличное значение tα,
следовательно коэффициент корреляции существенно отличен от нуля и зависимость
является достоверной.
Обычно корреляционный анализ всегда
дополняется регрессионным, а именно построением уравнения
зависимости между двумя переменными.
Зависимость может быть либо линейной,
либо нелинейной. В обоих случаях знание количественной
характеристики независимой переменной автоматически предопределяет знание
величины зависимой переменной. Определим линейную зависимость с
помощью следующего уравнения:
Y
= а + b · X,
где Y – оцениваемая
(или прогнозируемая) зависимая переменная;
а –
свободный член уравнения;
b – коэффициент регрессии, измеряющий среднее
отношение отклонения результативного признака от его средней
величины к отклонению факторного признака от его средней
величины;
Х – независимая переменная (или
факторный признак), используемая для определения зависимой
переменной.
Коэффициенты а и b рассчитываются на основе наблюдения величин X и Y с помощью
метода наименьших квадратов.
При этом строится следующая система
уравнений:
По данным таблицы 38 составим систему
уравнений:
 668,101067= 30*а
+ 1069,615*b;
668,101067= 30*а
+ 1069,615*b;
25092,5 = 1069,615*а + 42010*b.
Отсюда
а=10,5625; b = 0,328367; Y=
10,5625 + 0,328367*Х
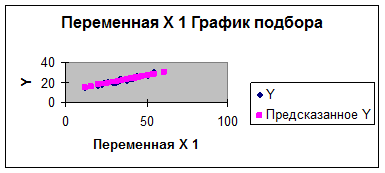
Уравнение регрессии позволяет
определить, как изменится результативный показатель при
изменении факторного, т.е. при увеличении относительного уровня затрат на 1% рентабельность увеличится
на 0,328 %.
Задание 3.
По результатам задания 1 с вероятностью 0,997 определите:
Ошибку выборки среднего уровня рентабельности организации, в которых будет
находиться средний уровень рентабельности в генеральной совокупности;
2) Для расчета границ
изменения средней характеристики генеральной совокупности по материалам выборки
воспользуемся формулами:
Х=Х+-∆ (1)
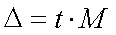 (2)
(2)
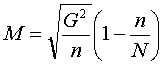 (3)
(3)
Х – средняя генеральной
совокупности;
Х – средняя выборочной
совокупности;
Таблица 5
|
число
предприятий
|
число
предприятий f
|
Середина
интервала Х
|
xf
|
|
от
14,9425-17,92822
|
4
|
16,43
|
65,72
|
|
от
17,92822-20,91394
|
6
|
19,41
|
116,46
|
|
от
20,91394-23,89966
|
8
|
22,4
|
179,2
|
|
от
23,89966-26,88538
|
6
|
25,38
|
152,28
|
|
от
26,88538-29,8711
|
6
|
28,37
|
170,22
|
|
Итого
|
30
|
|
683,88
|
|
Х сред
|
|
|
22,94
|
 Средняя выборочной совокупности равна
х
Средняя выборочной совокупности равна
х
t -
коэффициент доверия = 0,997 (по условию);т.е =3
М – средняя ошибки выборки
G2 –
дисперсия исследуемого показателя = 10,2
n – объем выборочной совокупности;=30
N – объем генеральной совокупности;=1500
n/N – доля выборочной совокупности в
объеме генеральной (или % отбора,
выраженный в коэффициенте)=0,02, которое дано по условию
Решение:
 Средняя выборочной совокупности равна
х=
Средняя выборочной совокупности равна
х=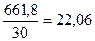
М рассчитываем по формуле 3.
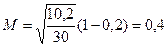
Рассчитаем предельную ошибку и определим границы изменения
средней по ф. (2)
-  предельная ошибка выборки;
предельная ошибка выборки;
Рассчитываем по формуле 2,
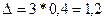
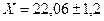
22,06-1,2<Х<22,06+1,2
20,86<Х<23,26
Т.о с вероятностью 0,997
можно утверждать, что рентабельность предприятия в генеральной совокупности
будет находиться в пределах от 20, 86 до 23,26 включая в себя среднюю по
выборочной совокупности.
2. Ошибку выборки доли организаций с уровнем рентабельности
23,9% и более и границы, в которых будет находиться генеральная доля
Ошибка выборки доли определяется по формуле
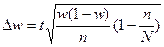
 , где t=2,
, где t=2, 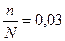 ;
;
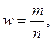 где m- число предприятий, в
нашем случае число предприятий с уровнем рентабельности 23,9 % и более, т.е. 12
предприятий.
где m- число предприятий, в
нашем случае число предприятий с уровнем рентабельности 23,9 % и более, т.е. 12
предприятий.
Ошибка выборки доли по нашему примеру:
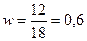
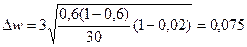
границы 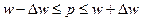 , или в нашем случае 0,6-0,075 ≤ р ≤ 0,6+0,075,
т.е. 0,5≤ р≤ 0,6;
, или в нашем случае 0,6-0,075 ≤ р ≤ 0,6+0,075,
т.е. 0,5≤ р≤ 0,6;
Задание 4.
Выпуск продукции и удельный расход стали по региону в текущем
периоде характеризуется следующими данными:
|
Вид продукции
|
Фактический выпуск
продукции
|
Расходы стали на единицу
продукции
по норме фактически
|
|
А
|
320
|
36
|
38
|
|
Б
|
250
|
15
|
12
|
|
В
|
400
|
10
|
9
|
Определите:
1. Индивидуальные индексы выполнения норм расхода стали.
2. Общий индекс выполнения норм расхода стали на весь выпуск
продукции.
3. Абсолютную экономию (перерасход) стали.
Решение:
Индекс – это показатель сравнения двух состояний одного и
того же явления (простого или сложного,
состоящего из соизмеримых или несоизмеримых элементов); включает 2 вида:
Отчетные, оцениваемые данные
("1")
Базисные, используемые в
качестве базы сравнения ("0")
1) Найдем индивидуальные индекс по
формуле:
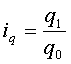 (где:
q – расходы,
q1, q2 - по норме и фактически)
(где:
q – расходы,
q1, q2 - по норме и фактически)
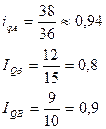 38>36 больше 1
38>36 больше 1
12<15 больше 1
9<10 больше 1
2) Найдем общие индексы по формулам:
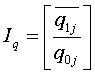 =
=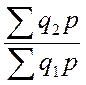
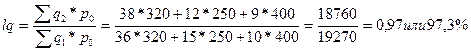
Общий индекс выполнения норм расхода равен 97,3 %.
3) Абсолютная экономия стали
|
Вид продукции
|
Факт выпуск продукции, ро
|
Расход стали на ед.
продукции
|
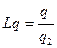
|
|
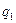
|
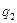
|
|
А
|
320
|
36
|
38
|
1,05
|
|
Б
|
250
|
15
|
12
|
0,8
|
|
В
|
400
|
10
|
9
|
0,9
|
Абсолютная экономия составляет:
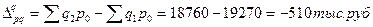
3.Аналитическая часть
3.1 Постановка задачи
Разность между показателями выборочной и генеральной совокупности
называется ошибкой выборки. Ошибки
выборки подразделяются на ошибки регистрации и ошибки репрезентативности.
Ошибки регистрации возникают
из-за неправильных или неточных сведений. Источниками таких ошибок могут быть
непонимание существа вопроса, невнимательность регистратора, пропуск или
повторный счет некоторых единиц совокупности, описки при заполнении формуляров
и т.д.
Среди ошибок регистрации выделяются систематические,
обусловленные причинами, действующими в
каком-то одном направлении и искажающими результаты работы (например,
округление цифр, тяготение к полным пятеркам, десяткам и т.д.), и случайные, проявляющиеся в различных направлениях, уравновешивающие друг
друга и лишь изредка дающие заметный суммарный итог.
Расхождение между значениями изучаемого
признака выборочной и генеральных совокупностей является ошибкой репрезентативности (представи-тельности). Она
может быть случайной и систематической. Случайная возникает в силу того, что
выборочное статистическое наблюдение является несплошным наблюдением, и выборка
недостаточно точно воспроизводит (репрезентирует) генеральную совокупность.
Систематические ошибка
репрезентативности возникают из-за неправильного, тенденциозного отбора единиц,
при котором нарушается основной принцип научно организованной выборки - принцип
случайности.
При определении величины репрезентативной ошибки предполагается, что
ошибка регистрации равна нулю. Определение ошибки производится по формулам ошибки выборочной доли и ошибки выборочной средней. Систематическая
ошибка репрезентативности возникает вследствие нарушения правил отбора единиц
генеральной совокупности, в частности принципа беспристрастного,
непреднамеренного отбора. Систематическая ошибка может привести к полной
непригодности результатов наблюдений.
По данным таблицы, нужно определить
насколько отличаются выборочные и генеральные показатели по данным об
успеваемости студентов (две 10%-е выборки):
|
Оценка
|
Число
студентов, чел
|
|
Генеральная
совокупность
|
Первая
выборка
|
Вторая
выборка
|
|
2
3
4
5
|
100
300
520
80
|
9
27
54
10
|
12
29
52
7
|
|
Итого
|
1000
|
100
|
100
|
3.1.2.Методика
решения задачи
Средний балл для генеральной совокупности
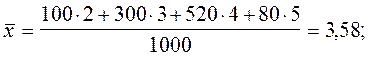
по первой выборке
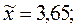
по второй выборке
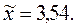
Доля студентов, получивших оценки
"4" и "5":
по генеральной совокупности
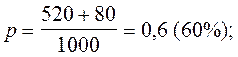
по первой выборке
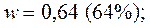
по второй выборке
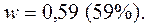
3.1.3.Технология выполнения компьютерных расчетов
Некоторые
расчеты выполнены с применением пакета программ обработки электронных таблиц
Табл. 2.
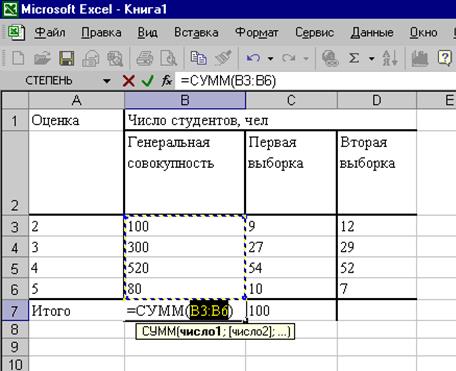
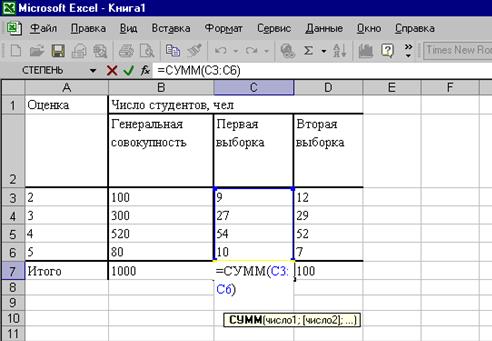
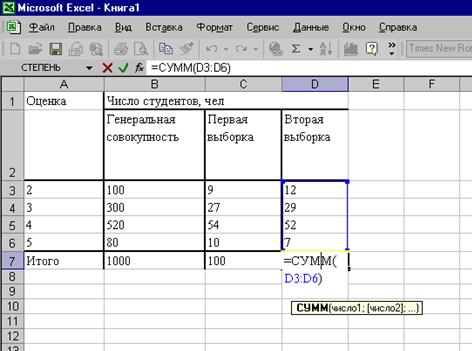
Результаты
расчетов, приведенных в табл.2
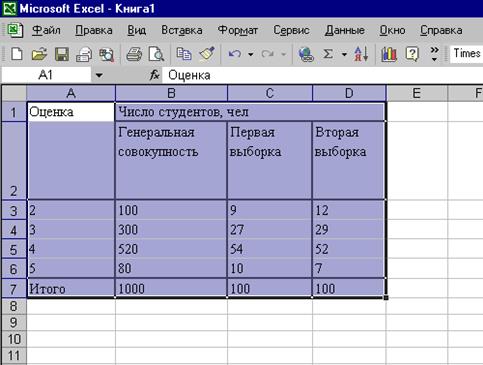
3.1.4. Анализ статистических расчетов.
Результаты
позволяют сделать следующие выводы:
Разность между
показателями выборочной и генеральной совокупности является случайной ошибкой
репрезентативности (ошибкой выборки).
Ошибки репрезентативности:
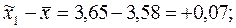
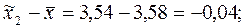
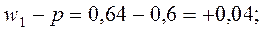
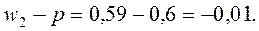
Как видно из расчетов, выборочная
средняя и выборочная доля являются случайными величинами, которые могут
принимать различные значения в зависимости от того, какие единицы совокупности
попали в выборку.
Заключение
Мы
выяснили, что выборочное наблюдение – это такое несплошное наблюдение, при
котором отбор подлежащих обследованию единиц осуществляется в случайном
порядке, отобранная часть изучается, а результаты распространяются на всю
исходную совокупность. Наблюдение организуется таким образом, что эта часть
отобранных единиц в уменьшенном масштабе репрезинтирует (представляет) всю
совокупность.
Совокупность
из которой производится отбор, называется генеральной, а все ее обобщающие
показатели – генеральными.
Совокупность
отобранных единиц именуют выборочной совокупностью, и все ее обобщающие
показатели – выборочными.
В
нашей практической части мы сделали группировку по признаку уровень
рентабельности продукции, выбрали пять групп с равными интервалами, определили
связь между признаками и рассчитали ошибку выборки среднего уровня, в
частности: рентабельность предприятия в генеральной совокупности будет
находиться в пределах от 20, 86 до 23,26 включая в себя среднюю по выборочной
совокупности.
И рассчитали ошибку выборки доли организаций с уровнем рентабельности
продукции 23,9% и более, и границы, в которых будет находиться генеральная
доля, в частности, генеральная доля находиться по нашему примеру с вероятностью
0, 997 в пределах 0,6-0,075 ≤ р ≤
0,6+0,075, т.е. 0,5≤ р≤ 0,6;
В аналитической части мы привели пример расчета ошибки
выборки по данным таблицы 2 ошибку выборочной доли и ошибку выборочной средней
и выяснили, что выборочная
средняя и выборочная доля являются случайными величинами, которые могут
принимать различные значения в зависимости от того, какие единицы совокупности
попали в выборку.
Выборочный метод широко используется в статистической практике для получения
экономической информации.
Большую актуальность приобретает выборочный метод в
современных условиях перехода к рынку. Вместе с тем, возрастающие требования к
менеджменту усиливают потребность в обеспечении надежной информацией,
дальнейшего повышения ее оперативности. Все это обуславливает более широкое
применение выборочного метода в экономике.
Потребность в использовании выборочного метода, выработке
вероятных суждений в современной отечественной статистике непрерывно
расширяется.
Литература
1.
Богородская Н.А. Статистика. Методы анализа статистической
информации: Текст лекций. СПб.: СПГААП. - 1997. - 80 с.
2.
Ефимова М.Р., Петрова Е.В.,
Румянцев В.Н. Общая теория статистики:
Учебник. М.: ИНФРА-М, 1998. - 416
с.
3.
Статистика: Курс лекций /Харченко Л.П., Долженкова В.Г., Ионин В.Г.
и др.; Под ред. В.Г.Ионина. -
Новосибирск: Изд-во НГАЭиУ, 1996. - 310 с.
4.
Общая теория статистики: Статистическая методология в изучении
коммерческой деятельности. Учебник /А.И.Харламов, О.Э.Башина,
В.Т.Бабурин и др.; Под ред.А.А.Спирина, О.Э.Башиной. М.: Финансы
статистика, 1994. - 296 с.
5.
Гусаров В.М. Теория статистики. - М.: Аудит, 1998. - 247 с.
6.
Елисеева И.И., М.М.Юзбашев. Общая теория статистики. - М.: Финансы и статистика, 1998. - 367 с.
7.
Теория статистики. Учебник/Под ред.Р.А.Шмойловой. - М.: Финансы и статистика, 1998. - 576 с.
8.
Ряузов Н.Н. Общая теория статистики: Учебник для студентов
экономич. спец. вузов. -4-е изд., перераб. и дополн. М.: Финансы и
статистика, 1984. - 343 с.
9.
Общая теория статистики / Под ред.Гольберга А.М., Козлова В.С. - М.:
Финансы и статистика, 1986. - 367 с.
10. Общая теория статистики / Под
ред.Боярского А.Я., Громыко Г.Л.. М.:
Изд-во МГУ, 1985. - 326 с.
11. Практикум по теории статистики:
Учебное пособие./ Под ред.
Р.А.Шмойловой. - М.: Финансы и статистика, 1998. 416 с.
12. Сборник задач по общей теории
статистики: Учебное пособие для
студентов вузов, обучающихся по специальности “Статистика” /
Овсиенко В.Е., Голованова Н.В., Королев Ю.Г. и др., -2-е изд., перераб.
и дополн. М.: Финансы и статистика,
1986. - 191 с.
13. Практикум по общей теории
статистики /Под ред. Ряузова Н.Н. - 2-е изд., перераб.и дополн. М.: Финансы и статистика,
1981. - 278 с.
Приложение 1
Таблица случайных чисел
|
5489
|
5583
|
3156
|
0835
|
1988
|
3912
|
0938
|
7460
|
0869
|
4420
|
|
3522
|
0935
|
7877
|
5665
|
7020
|
9555
|
7375
|
7124
|
7878
|
5544
|
|
7555
|
7579
|
2550
|
2487
|
9477
|
0864
|
2349
|
1012
|
8250
|
2633
|
|
5759
|
3554
|
5080
|
9074
|
7001
|
6249
|
3224
|
6368
|
9102
|
2672
|
|
6303
|
6895
|
3371
|
3196
|
7231
|
2918
|
7380
|
0438
|
7547
|
2644
|
|
7351
|
5634
|
5323
|
2623
|
7803
|
8374
|
2191
|
0464
|
0696
|
9529
|
|
7068
|
7803
|
8832
|
5119
|
6350
|
0120
|
5026
|
3684
|
5657
|
0304
|
|
3613
|
1428
|
1796
|
8447
|
0503
|
5654
|
3254
|
7336
|
9536
|
19441
|
|
5143
|
4534
|
2105
|
0368
|
7890
|
2473
|
4240
|
8652
|
9435
|
. 1422
|
|
9815
|
5144
|
7649
|
8638
|
6137
|
8070
|
5345
|
4865
|
2456
|
5708
|
|
5780
|
1277
|
6816
|
1013
|
2867
|
9938
|
3930
|
3203
|
5696
|
1769
|
|
1187"
|
0951
|
5991
|
5245
|
5700
|
5564
|
7352
|
0891
|
6249
|
6568;
|
|
4184
|
2179
|
4554
|
9083
|
2254
|
2435
|
2965
|
5154
|
1209
|
7069
|
|
2916
|
2972
|
9885
|
0275
|
0144
|
8034
|
8122
|
3213
|
7666
|
0230
|
|
5524
|
1341
|
9860
|
6565
|
6981
|
9842
|
0171
|
2284
|
2707
|
3008
|
|
0146
|
5291
|
2354
|
5694
|
0377
|
5336
|
6460
|
9585
|
3415
|
2358
|
|
4920
|
2826
|
5238
|
5402
|
7937
|
1993
|
4332
|
2327
|
6875
|
5230
|
|
7978
|
1947
|
, 6380
|
3425
|
7267
|
7285
|
1130
|
7722
|
0164
|
8573
|
|
7453
|
0653
|
3645
|
7497
|
5969
|
8682
|
4191
|
2976
|
0361
|
9334
|
|
1473
|
6938
|
4899
|
5348
|
1641
|
3652
|
0852
|
5296
|
4538
|
4456
|
|
8162
|
8797
|
8000
|
4707
|
1880
|
9660
|
8446
|
1883
|
9768
|
0881
|
|
5645
|
4219
|
0807
|
3301
|
4279
|
4168
|
4305
|
9937
|
3120
|
5547
|
|
2042
|
1192
|
1175
|
8851
|
6432
|
4635
|
5757
|
6656
|
1660
|
5389
|
|
5470
|
7702
|
6958
|
9080
|
5925
|
8519
|
0127
|
9233
|
2452
|
7341
|
|
4045
|
1730
|
6005
|
1704
|
0345
|
3275
|
4738
|
4862
|
2556
|
8333
|
|
5880
|
1257
|
6163
|
4439
|
7276
|
6353
|
6912
|
0731
|
9033
|
5294
|
|
9083
|
4260
|
5277
|
4998
|
4298
|
5204
|
3965,
|
4028
|
8936
|
5148
|
|
1762
|
8713
|
1189
|
1090
|
8989
|
7273
|
3213
|
1935
|
9321
|
4820
|
|
2023
|
2589
|
1740
|
0424
|
8924
|
0005
|
1969
|
1636
|
7237
|
1227
|
|
7965
|
3855
|
4765
|
0703
|
1678
|
0841
|
7543
|
0308
|
9732
|
1289
|
|
7690
|
0480
|
8098
|
9629
|
4819
|
7219
|
7241
|
5128
|
3853
|
1921
|
|
9292
|
0426
|
9573
|
4903
|
5916
|
6576
|
8368
|
3270
|
6641
|
0033
|
|
0867
|
1656
|
7016
|
4220
|
2533
|
6345
|
8227
|
1904
|
5138
|
2537
|
|
0505
|
2127
|
8255
|
5276
|
2233
|
3956
|
4118
|
8199
|
6380
|
6340
|
|
6295
|
9795
|
1112
|
5761
|
2575
|
6837
|
3336
|
9322
|
7403
|
8345
|
|
6323
|
2615
|
3410
|
3365'
|
1117
|
2417
|
3176
|
2434
|
5240
|
5455
|
|
8672
|
8536
|
2966
|
5773
|
5412
|
8114
|
0930
|
4697
|
6919
|
4569
|
|
1422
|
5507
|
7596
|
0670
|
3013
|
1351
|
3886
|
3268
|
9469
|
2584
|
|
2653
|
1472
|
5113
|
5735
|
1469
|
9545
|
9331
|
5303
|
9914
|
6394
|
|
0438
|
4376
|
3328
|
8649
|
8327
|
0110
|
4549
|
7955
|
5275
|
2890
|
|
2851
|
2157
|
0047
|
7085
|
1129
|
0460
|
6821
|
8323
|
2572
|
8962
|
|
7962
|
2753
|
3077
|
8718
|
7418
|
8004
|
1425
|
3706
|
8822
|
1494
|
|
3837
|
4098
|
0220
|
1217
|
4732
|
0150
|
1637
|
1097
|
1040
|
7372
|
|
8542
|
4126
|
9274
|
2251
|
0607
|
4301
|
8730
|
7690
|
6235
|
3477
|
|
0139
|
0765
|
8039
|
9484
|
2577
|
7859
|
1976
|
0623
|
1418
|
6685
|
|
6687
|
1943
|
4307
|
0579
|
8171
|
8224
|
8641
|
7034
|
3595
|
3875
|
|
6242
|
5582
|
5872
|
3197
|
4919
|
2792
|
5991
|
4058
|
9769
|
1918
|
|
6859
|
9606
|
0522
|
4993
|
0345
|
8958
|
1289
|
8825
|
6941
|
7685
|
|
6590
|
1932
|
6043
|
3623
|
1973
|
4112
|
1795
|
8465
|
2110
|
8045
|
|
3482
|
0478
|
0221
|
6738
|
7323
|
5643
|
4767
|
0106
|
2272
|
9862
|