1.Основные проблемы высокоинформативной локации

1.1. Моделирование методов высокоинформативной локации

   Одной из наиболее важных задач высокоинформативной локации (в частности, радиолокации) является формирование локационного изображения (ЛИ) объектов, под которым понимают пространственное распределение физических характеристик этих объектов, получаемое в результате анализа рассеянного ими электромагнитного поля. Информация о локационном изображении содержится в локационном сигнале неявно. Современный этап развития радиолокации характеризуется стремлением получить максимум информации из данных локационного зондирования, которые полностью определяются частотными, амплитудно-фазовыми, поляризацион-ными и угловыми характеристиками отражённого сигнала.

   В процессе локации важно определить как номенклатуру, так и количественные параметры функциональных элементов изучаемых объектов, их взаимное расположение в пространстве. Поскольку структура объектов трёхмерна, то общая идея высокоинформативной локации сводится к последовательному анализу сечений. Процедура поиска и идентификации функциональных элементов объекта локации основывается на выявлении различий в характеристиках объекта и сопровождающего его фона. Анализ этих различий позволяет провести обнаружение объекта. Установление различий может осуществляться путём регистрации изменений амплитуды, фазы, частоты, поляризации и направления распространения радиоизлучения, отражаемого от объекта.

   Комплексная напряжённость электрического поля плоской волны Е с частотой w = kc и фазой j при её распространении вдоль оси z описывается выражением

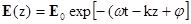                                                     (1.1)

   После взаимодействия с объектом электрическое поле оказывается в общем случае измененным по направлению распространения, ампли­туде, фазе, частоте и поляризации:

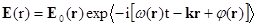                                     (1.2)

   Изменение амплитуды волны связано с поглощением и рассеянием, дефазирующие свойства объекта определяются различием показателей преломления вещества объекта и окружающей среды. Вследствие движения объекта может происходить изменение частоты волны по сравнению с первоначальной. Изменение поляризации волны обусловлено зависимостью коэффициента отражения от угла падения для волн с различной пространственной ориентацией относительно плоскости падения.

   Если удаётся измерить интенсивность, поляризацию, частоту и фазу волн, рассеянных объектами, как функцию углов рассеяния, то этой информации в принципе достаточно для получения количественного описания геометрических параметров объекта. Как показал Адамар, вычислительная схема подобных задач весьма чувствительна к небольшим ошибкам регистрируемых данных. Сужение общности постановки задачи, использование дополнительной информации о структуре объектов позволяет регуляризовать обратную задачу - избавиться от неоднозначности в её решении.

   Отражённый сигнал в дальней зоне является суперпозицией отражений от отдельных точек объекта и зависит от конфигурации, мате­риала объекта и его ориентации относительно радиолокационной станции (РЛС). При фиксированном ракурсе объекта принимаемый сигнал можно рассматривать как его интегральное представление (проекцию). Следовательно, формирование ЛИ сводится к его восста­новлению по проекциям - томографии.

   Задача восстановления двумерной функции по её интегралам вдоль прямых линий впервые была поставлена Радоном [17] и соответствую­щее преобразование носит его имя. В последующем приложения томографического подхода развивались успешно во многих областях науки и техники. Первые применения томографического подхода связаны именно с обработкой высокоинформативных сигналов. В рамках томографического подхода развиваются многочисленные методы формиро­вания высококачественного изображения объектов с помощью РЛС, использующих как монохроматические, так и сверхширокополосные (СШП) сигналы. Вместе с этим аппарат томографического подхода является достаточно новым, и для его эффективного использования необходимо решать немало проблем физического и математического характера.

   В случае использования узкополосных сигналов для описания ЛИ используется комплексная функция

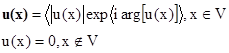                                           (1.3)

г

де 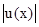 - амплитудный коэффициент отражения в точке объекта, координаты которой задаются вектором x; 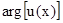 - фазовый сдвиг сигнала при отражении от точки x, V - область пространства, занимаемая объектом; 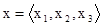 - вектор координат в трехмерном евклидовом пространстве.

   Физический смысл функции u(x) состоит в том, что её значение по­лучается сканированием всей поверхности объекта бесконечно узким (игольчатым) лучом с помощью приёмно-передающей аппаратуры. При этом используется монохроматический (узкополосный) сигнал, а получаемые значения функции (1.3) характеризуют свойства объекта на несущей частоте w₀ при измерениях в дальней зоне. Часто условия наблюдения объекта позволяют получать лишь его двумерные изображения. В этом случае вектор x включает две компоненты и получаемое изображение представляет собой проекцию функ­ции (1.3), например, на плоскость (x₁ ,x₂):

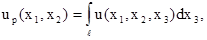                                                 (1.4)

где l - размер объекта вдоль оси x₃.

   Если для формирования ЛИ используется СШП сигнал, то описанием изображения служит функция вида:

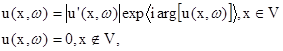                            (1.5)

где 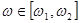 - частота в интервале от нижней w₁, до верхней w₂, границ спектра сигнала.

   Очевидно, функция (1.3) представляет собой частный случай (1.5) при . Функция (1.5) представляет собой частотную характеристику каждой точки объекта. Пользуясь связью частотных и импульсных характеристик, можно ввести для описания ЛИ, получаемого с помощью СШП сигналов, ещё одну функцию - Фурье преобразование (образ) . Однако широкого применения эти модели не получили ввиду сложности их интерпретации. Действительно, понятие оптического изображения отождествляется с пространственной картиной, т.е. функцией только пространственных координат, а функция (1.5) и её Фурье-образ представляют собой наборы таких картин. Содержащийся в них объём информации зачастую превышает необходимый объём.

   К основным понятиям томографического подхода относятся проекции изображения, связь между проекцией и изображением, устанавливаемая преобразованием Радона и способы отыскания изображения по известным (в общем случае неточным и/или неполным) проекциям. Кратко рассмотрим эти понятия. Пусть функция 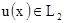 определена в евклидовом пространстве 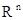. Введём в  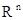подпространства  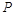и 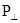 с размерностями k и n - k, соответственно. 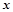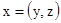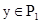Тогда вектор  представляется двумя компонентами , где , а 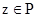. Обобщённой проекцией (преобразованием в k-мерных плоскостях) функция  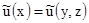называется интеграл вида

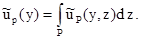                                                         (1.6)

   В общем случае имеет место неравенство 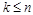. В частности, при  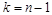размерность подпространства 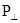 равна единице и вектор 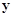 характеризует набор различным образом ориентированных линий. В  этом случае вместо термина "проекция" обычно употребляется термин "преобразование Радона" функции 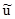. Оно ставит в соответствие n - мерной функции  набор её интегралов по гиперплоскостям. Указанное интегральное преобразование (1.6) ставит в соответствие n - мерной функции  набор её интегралов по гиперплоскостям 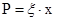, каждая из которых имеет размерность n - 1, ориентирована ортом  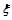и удалена от начала координат 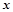 на расстояние P. При  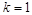подпространство P вырождается в семейство линий и функция  интегрируется вдоль этих линий.

   В общем виде задача восстановления изображения по проекциям состоит в нахождении функции  по известной функции . Задачи восстановления объектов по информации об их проекциях, функций по их интегральным преобразованиям рассматриваются во многих разделах математики. Очень часто возникает потребность решения подобного рода обратных задач по неполным наборам данных. Как показал Зюсс [18], если проекции двух выпуклых компактов (объектов) в 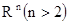 на любую гиперплоскость совмещаются параллельным переносом, то и сами эти компакты совмещаются в 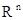 параллельным переносом. В работах [12,19,20] были получены обобщения этого утверждения на случаи, когда компакты не выпукла или когда их проекции совмещаются не параллельными переносами, а движениями, причём информация о таких проекциях известна не для любого направления проектирования.

   Геометрические характеристики рассеивателя радиоизлучения фигурируют в коэффициентах асимптотических разложений решений задачи радиолокации, т.е. амплитуд электромагнитного поля, рассеянного облучаемым объектом. В частности, в приближении геометрической оптики асимптотическое разложения амплитуды рассеяния содержит в качестве главного члена разложения слагаемое с гауссовой кривизной границы выпуклого рассеивателя. Геометрическая информация такого рода позволяет в ряде практически важных случаев определить форму рассеивающего объекта, т.е. решить обратную задачу рассеивания.

   Задача вычисления функции по её преобразованию Радона некорректна, что, в частности, проявляется в неединственности решения, вызванной ограничением области определения функции 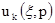 - преобразования Радона функции  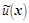- по переменным и (или) p. Другой причиной некорpектности является неустойчивость операции численного дифференцирования при наличии ошибок измерения 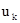. Указанные обстоятельства имеют важное значение для радиолокации, поскольку сигналы, используемые для получения ЛИ, сопровождаются помехами, а отдельные детали объекта, как правило, наблюдаются не при всех ракурсах.

   Основными особенностями радиолокационного применения томографии являются следующие. Во-первых, модели ЛИ отличаются от моделей, используемых в традиционном для томографии рентгеновском диапазоне. Последние описывают поглощение поля при просвечивании объекта, а содержанием ЛИ, как правило, являются характеристики рассеяния и (или) геометрическая форма объекта. Во‑вторых, для радиолокации характерно ограничение сектора, числа ракурсов наблюдения объекта и ширины спектра зондирующего сигнала, а также воздействие на процесс формирования ЛИ различных помех. Поэтому особое значение имеет разработка и использование томографических методов формирования ЛИ, учитывающих эти факторы. Необходимы также эффективные способы высокоточного сопровождения объекта по дальности при формировании его ЛИ. Создание таких методов должно основываться на достижениях как квантовой электроники, так и квантовой статистики. Значительный объём вычислений и большие массивы данных предъявляют жёсткие требования к устройствам обработки сигналов и приводят к необходимости разработки эффективных вычислительных алгоритмов. В настоящее время для нахождения проекций ЛИ по измеренным сигналам используется обычно приближение геометрической оптики, которое по существу является приближением первого порядка. Оно не учитывает квантовых эффектов и, строго говоря, применимо к ограниченному классу объектов. Это приводит к определённым потерям качества ЛИ.

   В целом использование томографических методов в радиолокации даёт ценные результаты для практики и открывает много направлений для перспективных исследований.

1.2. Топологический анализ решений обратных задач рассеяния в радиолокации

   Объём возможных измерений в реальных ситуациях весьма ограничен, и возникает проблема оптимального использования имеющейся информации, повышения качества информации. Возможность повысить качество имеющейся измерительной информации связана с использованием априорной информации об объекте измерений, которая обычно формулируется в виде математической модели измерений.

   Как с физической, так и с математической точек зрения вопросы рассеяния весьма сложны, вследствие чего при их изучении используются обычно асимптотические методы. Параметрами асимптотических разложений являются, как правило, частоты полей и расстояния от рассеивателя до пунктов измерения. В асимптотическом разложении измеряемой величины в качестве коэффициентов возникают при этом геометрические характеристики рассеивателя (например, площадь ортогональной проекции на плоскость, гауссова кривизна границы и т.п.). Геометрическая информация такого рода позволяет в некоторых случаях определять характеристики рассеивающего объекта. Использование геометрических и топологических методов решения таких задач приводит к новым, а иногда и к исчерпывающим результатам.

   При решении волновых уравнений обратной задачи рассеяния для коэффициентов асимптотического разложения амплитуды поля в дальней зоне строится рекуррентная система, такая, что задача решения её уравнений проще задачи решения исходных уравнений. Асимптотически решения исходных уравнений имеют в качестве главного члена решения приближённых уравнений. Упрощения алгоритма решения приближённых уравнений и, следовательно, обратной задачи рассеяния связаны с решением вопроса о таком построении рекуррентной системы, чтобы она обладала наперед заданной симметрией, т.е. допускала некоторую группу преобразований. Решения обратной задачи рассеяния могут быть найдены на основе исследований связи между группой преобразований, допускаемых приближёнными уравнениями, и группой, допускаемой системой исходных волновых уравнений, а также влияния процесса моделирования рассеяния волнового поля на эту связь.

   Поскольку геометрические и топологические методы эффективны именно для асимптотик, то первостепенно важным является изучение проблем единственности и устойчивости решения обратных задач рассеяния радиоизлучения. Способы исследования обратных задач восстановления рассеивателя радиоизлучения основываются на выделении главной геометрической интегральной информации, связанной с интенсивностью рассеянного волнового поля.

    Топологический анализ проблемы высокоинформативной локации в реальной ситуации может свестись к исследованию единственности решения обратных геометрических задач, связанных с просвечиванием или рассеянием на малые углы. Задачу определения финитной функции Ф(x), x Î Rⁿ   по известным интегралам

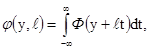                                                     (1.7)

где y принадлежит проходящей через начало координат плоскости, ортогональной единичному вектору l , часто называют обратной задачей томографии. В данной формулировке она адекватна также обратной задаче рассеяния на малые углы. Если I₀  и I -интенсивности светового пучка до его падения на исследуемый объект (поверхность), и, следовательно, после взаимодействия с объектом, то имеем:

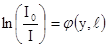                             .                                (1.8)

   Поэтому функцию 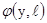 можно интерпретировать как фотоснимок или фотопроекцию в направлении l. В общем случае решение такой задачи требует бесконечного числа измерений, т.е. функция 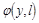 должна быть известна для бесконечного числа направлений l. В практической деятельности представляют интерес ситуации, в которых обратную задачу просвечивания (томографии) надо решать приближенно, но по конечному числу измерений. В некоторых случаях конечного числа измерений бывает достаточно доя точного решения такой задачи. Например, если  Ф(x)‑характеристическая функция выпуклого компакта B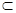Rⁿ, то ее удается однозначно восстановить почти по любой четверке измерений вдоль направлений, лежащих в одной плоскости.

   Если P - множество направлений из двумерной плоскости в Rⁿ такое,  что оно линейно неэквивалентно подмножеству направлений диагоналей правильного многоугольника, то рентгеновские снимки (или штейнеровские симметризации) вдоль направлений из P позволяют различать выпуклые тела из Rⁿ . Существенность условия на направления  P иллюстрируются следующим примером: если K - правильный m- угольник, а L получен из K поворотом вокруг центра  на угол p / m, то фотоснимки  K и L вдоль направлений сторон выпуклой оболочки conv(KÈL), как легко видеть, совпадают. Если BÌ Rⁿ - многогранник, то число направлений, достаточных для восстановления B по фотоснимкам может быть уменьшено. Почти любая пара фотоснимков просвечивания позволяет однозначно восстановить однородный многогранник B Ì R³.

   Пары направлений m, l, позволяющих восстановить многогранник B, устроены так: требуется, чтобы проекции непересекающихся ребер B на плоскости, ортогональные m, l, могли пересекаться только своими внутренними частями, а разные вершины B должны проектироваться на прямую, по которой пересекаются ортогональные m и l-  плоскости в разные точки. В виду того, что функция просвечивания 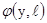 в этом случае кусочно-линейна и разрывы ее линейности происходят на проекции ребер B, мы можем реконструировать одномерный остов B по этим линиям разрывов. Для выпуклого B таких комбинаторных соображений уже достаточно для его восстановления даже в n - мерном случае. Чтобы натянуть на одномерный остов двумерные грани невыпуклого B Ì R³ необходимо рассматривать количественно поведение функций просвечивания, а не только качественно.

   Почти любая пара снимков просвечивания однозначно определяет форму и положение выпуклого гладкого однородного тела вращения вR³. Здесь почти любая пара снимков позволяет определить ось вращения тела. Исключение составляют случаи, когда прямые пересечения плоскостей снимков перпендикулярны осям их симметрий. Зная же ось вращения и один снимок, форму тела можно восстановить однозначно. Пусть теперь в Rⁿ   имеется набор из N точек. Ортогональную проекцию этого набора на прямую с учетом кратности будем называть “одномерной томограммой”. Физическим основанием данного определения является тот факт, что при слиянии изображений нескольких точек на экране яркость их изображений обычно складывается, что позволяет различать, в какую точку прямой какое количество точек из искомого набора проектируется.

   N  точек в пространстве Rⁿ , n ³ 2  однозначно определяются своими одномерными томограммами на N (n- 1)+1 попарно непараллельную прямую 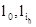; 1£ i_к  £ N,  1£ к £ n, у которых проекции искомых точек на прямую l₀ различны, направляющие векторы прямых l_1,к ,..l_1,n-1 , l₀ образуют базис в Rⁿ, а остальные (N - 1)×(n - 1) прямые расположены так, что при всех K прямые l_1,к ,.. l_N,к параллельны двумерной плоскости, натянутой на направляющие векторы прямых l₀ , l_1,к  .

   Доказательство проводится индукцией по n. При n = 2 теорема доказывается индукцией по N. Проекции N точек плоскости на N доказывается индукцией по N. Проекции N точек плоскости на N прямых позволяют построить выпуклый многоугольник, у которого некоторые из искомых точек являются вершинами. Проекция на (N+1) -ю прямую позволяет идентифицировать по крайней мере одну из искомых точек. Условие несовпадения проекций точек на прямую l₀, по-видимому, можно опустить; однако при невыполнении этого условия чисто комбинаторные проблемы затрудняют построение алгоритма искомых точек.

   Основные результаты настоящего раздела относятся к классической проблеме, которая в разных формулировках рассматривалась многими авторами: если у двух выпуклых тел ортогональные проекции на любую плоскость одинаковы, то что можно сказать об этих телах. Всюду в дальнейшем, если не оговорено противное, будет предполагаться, что n > 2  и что все проекции ортогональны.

   В работе [19] показано, что если у двух аналитических замкнутых выпуклых поверхностей в R³ проекции на любую плоскость имеют совпадающие длины границ и площади, то такие поверхности равны. С.Кампи [21] указал на необходимость условия аналитичности в теореме Аниконова - им были построены пары выпуклых бесконечно гладких равносоставленных, но неравных тел вращения, имеющих постоянную ширину и таких, что параметры их проекций также,  как и площади, совпадают.

   Пусть 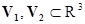- объекты, у которых проекции на любую плоскость совмещаются сохраняющим ориентацию движением (собственно конгруэнтны) и 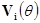 - проекция объекта  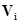на плоскость с единичной нормалью 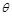, а 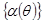- множество таких углов 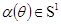, что проекция  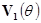совмещается с  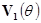поворотом на 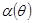. Знак угла определяется направлением нормали  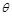и поэтому 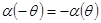. Если фигуры  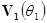не имеют симметрий относительно вращений, то для такого 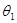 угол 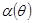 определяется однозначно и является непрерывной функцией в некоторой окрестности 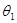. В противном случае функция  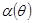многозначна и может, вообще говоря, иметь разрывы в окрестности .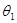

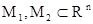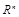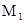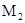   Если  - связные компактные аналитические гиперповерхности без края и их проекции на любую двумерную плоскость в  собственно конгруэнтны и выпуклые оболочки этих проекций не имеют симметрий относительно вращений, то  и  совмещаются в 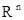либо параллельными переносами, либо центральной симметрией. Если 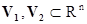 - компактные выпуклые объекты и их проекции на любую двумерную плоскость собственно подобны и не имеют симметрий относительно вращений (коэффициенты подобия не предполагаются, вообще говоря, постоянными, не зависящими от плоскости), то 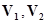 совмещаются в  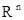гомотетией или параллельным переносом.

   Компактный объект 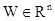 называется k - обозримым, если через каждую  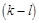- мерную плоскость, не пересекающуюся с 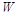, можно провести k - мерную плоскость, также с  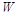не пересекающуюся; 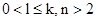. Если  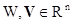являются (n - 2) - обозримыми множествами и их проекции на любую двумерную плоскость собственно конгруэнтны, а выпуклые оболочки этих проекций не имеют симметрий относительно вращений, то 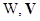 совмещаются в  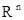либо параллельным переносом, либо центральной симметрией. Пусть 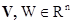- односвязные (n - 2) - обозримые множества и их проекции на любую двумерную плоскость собственно конгруэнтны и не имеют симметрий относительно вращений, тогда 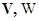 совмещаются в  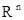либо параллельным переносом, либо центральной симметрией.

   Для описания реальных локально негладких процессов в последние годы эффективно используется теория фракталей, т.е. множеств дробной размерности [24]. Фрактальные модели применяются в ситуации априорной неопределённости, когда измерительных данных недостаточно для определения статистических характеристик регистрируемых процессов. В условиях ограниченного объёма радиолокационных измерений использование фрактально-геометрической аппроксимации может повысить точность и достоверность локационной информации, представив её в более удобном для анализа виде, включая топологический анализ обратных задач рассеяния.

1.3. Определение условий единственности и устойчивости обратных задач в радиолокации

   Рассмотрим условия единственности и устойчивости обратной задачи, состоящей в определении формы отражателя по характеристикам рассеянного излучения. Результаты исследований единственности и устойчивости процедур восстановления объекта по его проекциям, изложенные в работах [12,18-20,168-172], с применением геометрического приближения для поля могут быть использованы для решения вопросов единственности и устойчивости обратных задач в радиолокации. К требуемой единственности или к сужению класса решений обратной задачи приводит также использование некоторых априорных сведений об объекте, включая сведения общего характера о свойствах его поверхности и т.п.

   Для отражателя с произвольной гладкой выпуклой поверхностью геометрическая теория восстановления его формы была построена Келлером [25]. Обозначим через s(q,j) дифференциальное сечение рассеяния в направлении q, j, которое вызывается плоской волной, падающей на отражатель вдоль оси x. В точке A(q,j) на отражающей поверхности, из которой волна отражается вдоль направления q, j, нормаль к отражателю в соответствии с законом отражения должна быть направлена по (q/2j)  и угол падения равен q / 2. Гауссова кривизна поверхности в точке отражения G(q /2,j) и коэффициент отражения   R(q /2)  связаны соотношением:

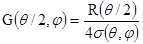                                                          (1.9)

   Если коэффициент отражения определен с помощью априорных сведений о материале поверхности, а дифференциальное сечение рассеяния s  измерено, то гауссова кривизна определяется на полусфере 0 £ q £ p/2  единичной сферы. Значениями гауссовой кривизны, найденными для каждой нормали к поверхности, определяется в свою очередь форма отражателя радиоволн. Доказательство единственности определения выпуклой замкнутой поверхности, когда для каждой нормали к поверхности задана ее гауссова кривизна, впервые получено Минковским [11]. Путем облучения поверхности из противоположного направления можно получить значения гауссовой кривизны и на полусфере p/2 £ q £ p, откуда следует единственность решения обратной задачи. Более простым примером является рассеяние плоской волны на поверхности вращения. Если волна падает вдоль оси вращения отражателя, то 4G = dq/dy  и из (1.9) следует:

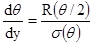                                                                    (1.10)

Используя соотношение

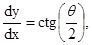                                                                    (1.11)

получаем поверхность, определяемую системой параметрических уравнений:

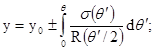                                                      (1.12)

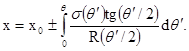
   Простые формулы для конкретных геометрических поверхностей и разнообразных типов облучения объектов электромагнитными волнами приведены в работе [25]. Для выпуклых объектов, имеющих центр симметрии, как хорошо известно, знание всего одной числовой функции, зависящей от направления p в пространстве, позволяет однозначно и устойчиво определять как форму исследуемого объекта, так и его положение в пространстве. Примером такого рода функций является площадь S(p) проекции объекта на плоскость, ортогональную направлению p, или периметр такой проекции L(p).

   Для тел, не обладающих симметриями, такой числовой информацией (в виде S(p) или L(p) - функций двух переменных) недостаточно для восстановления формы выпуклого объекта. Поэтому в качестве исходных данных для решения таких реконструкционных задач берутся формы всех проекций этого объекта. Такие данные несложным образом появляются в приближении геометрической оптики и представляют собой численные функции трёх переменных. Их областью определения является группа SO(3).

   Установлено, что в условиях отсутствия симметрий относительно поворотов у всех таких проекций любые два тела в пространстве, имеющие одинаковые проекции, имеют сами одинаковую форму, поскольку совмещаются либо параллельным переносом, либо центральной симметрией. Следовательно, наличие числовой информации о проекциях обеспечивает единственность решения задачи восстановления формы объекта. Если же формы проекций объектов одинаковы с точностью до изменения масштаба, то исходные объекты тоже имеют одинаковую форму в пространстве, с точностью до изменения масштаба, так как могут быть совмещены гомотетией или параллельным переносом. Аналогичные утверждения об условиях единственности решения задач восстановления формы справедливы и для обозримых тел. Компактный объект определяется как обозримый, если через каждую точку, не лежащую в нём, можно провести прямую, не пересекающую это тело. Указанное выше условие отсутствия симметрий у проекции обозримых объектов существенно, что показывают соответствующие контрпримеры [20].

   Для высокоинформативной локации важное значение имеет определение условий устойчивости решений задач реконструкции объектов по формам их проекций. Если два выпуклых объекта при проектировании на любую плоскость дают фигуры, совмещаемые некоторым движением этой плоскости с относительной точностью до достаточно малого 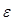, то исходные выпуклые объекты с точностью до величины порядка 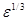 имеют одинаковую форму, поскольку с примерно такой точностью могут быть совмещены в пространстве либо параллельным переносом, либо центральной симметрией. Оценок устойчивости решения таких задач для обозримых объектов не существует. Однако в классе тел, более узком, чем обозримые компакты, но более широком, чем выпуклые, существование таких оценок можно установить.

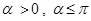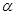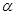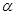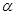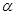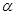   Пусть угол . Назовём компактный объект W втранстве - вогнутым, если через каждую точку, не лежащую в W, можно провести двугранный угол величины , внутренность которого с W  не пересекается. Для острых углов  оценки устойчивости, как и для обозримых тел, нет, однако для тупых углов  формы  - вогнутых объектов устойчивым образом восстанавливаются по формам проекций этих объектов. Рассмотрим - вогнутые компакты, содержащиеся в шаре 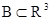. Из общей теории условно-корректных задач [8] вытекает, что для достаточно малого 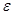 > 0 найдётся такое 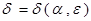, что если у двух 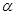-вогнутых компактов, лежащих в В, проекции на любую гиперплоскость 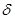- близки, то сами эти компакты 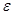 - близки в пространстве .

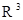   Для решения обратной задачи дифракции пользуются приближением Кирхгофа, которое состоит в том, что поле на препятствии считается равным нулю, а вне препятствия - таким же, как и в отсутствие препятствия вообще. Метод восстановления формы рассеивателя, использующий приближение Кирхгофа для описания рассеянного поля в дальней зоне, был предложен Льюэсом [26] и применён Проссером [27] при рассмотрении рассеяния плоской волны мягкой границей. Рекуррентная формула для решения обратной задачи дифракции по значениям векторного поля в дальней зоне получена Уилкоксом [28]. Формулировка условий единственности и устойчивости решений задач локации выпуклых и невыпуклых объектов (например, 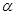 - вогнутых объектов) отвечает теоремам определения выпуклых и невыпуклых многообразий по их проекциям и выпуклым частям оболочек [12,19,20].

   Вопросы единственности и устойчивости решений задач высокоинформативной нефелометрии были рассмотрены нами ранее в приближении геометрической оптики. Обратимся теперь к моделям рассеяния, основанным на приближении Борна первого порядка [26]. Оно известно также, как приближение Кирхгофа для интегральных уравнений, описывающих рассеяние идеальными проводниками.

   Скалярное поле 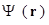, удовлетворяющее уравнению

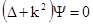                                                                       (1.13)

в области, которая не содержит рассеивающий объект, является суперпозицией приходящих волн 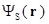 и рассеянного поля 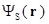. Рассеяние вызывается распределением потенциала или конeчной средой, описываемой показателем преломления. Возникает проблема определения поля между рассеивателем и поверхностью P, лежащей вне рассеивателя, по значению поля на P. Аналогичной электромагнитной задачей является восстановление векторного поля A, удовлетворяющего уравнению

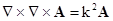                                                                 (1.14)

вне рассеивателя по его значениям на поверхности  P .

   Рассмотрим рассеяние плоской монохроматической бегущей  электромагнитной волны

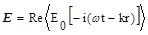                                                     (1.15)

на идеально проводящем объекте объёма 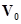, ограниченном замкнутой поверхностью 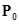. Из условия

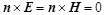                                                               (1.16)

для векторов электрического и магнитного полей (E и H соответственно, n - нормаль к поверхности 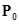) на поверхности идеального проводника следует, что для достаточно гладких функций a и 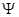 справедливо уравнение

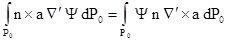                  .             (1.17)

Отсюда следует соотношение

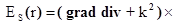                                             (1.18)

                  

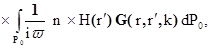
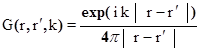                 .                     (1.19)

Для больших r из (10) имеем выражение

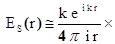                                                            (1.20)

где s - единичный вектор в направлении точки наблюдения r .

   Приближению Борна первого порядка будет соответствовать соотношение, полученное из (1.20) пр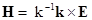и  и 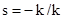, причём в качестве H взято значение приходящего поля:

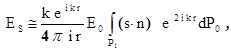                                (1.21)

где поверхностный интеграл берётся по рассеивающей части поверхности 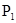. Рассеяние волновой функции  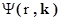от границы  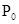описывается уравнением Гельмгольца (1.13) и граничными условиями:

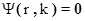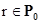                      ,      .                            (1.22)

   Решение системы уравнений (1.13) и (1.22), отвечающее начальной плоской волне и рассеянному полю, даётся решением интегрального уравнения

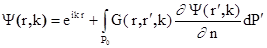                      (1.23)

которое может быть представлено через ряды Неймана. Если этот ряд сходится, то решение уравнения (1.23) имеет вид

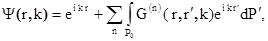                      (1.24)

где функции 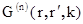 связаны рекуррентными соотношениями:

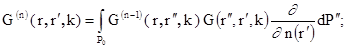  (1.25)

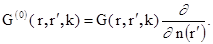                                    (1.26)

При больших значениях r поведение функции 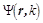 описывается уравнением

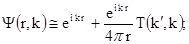                                          (1.27)

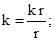                                                                           (1.28)

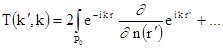                                 (1.29)

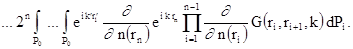
Применив преобразования Фурье, можно преобразовать уравнение для амплитуды рассеяния 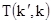 в уравнение с интегральными степенными рядами [29], формальное решение которого может основываться на использовании данных обратного рассеяния по всем энергиям и со всех сторон.

   Рассмотрим возможности определения рассеивающего потенциала или показателя преломления по рассеянному полю, образованному суперпозицией монохроматических плоских волн. Если совокупность монохроматических плоских волн

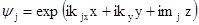                ,                      (1.30)

где

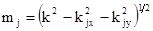                                                    (1.31)

и числа 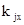 являются бесконечной ограниченной системой вещественных чисел таких, что выражение (1.31) вещественно, рассеивается потенциалом U с конечным носителем массы m, то рассеянная волна 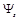 в приближении Борна первого порядка имеет вид:

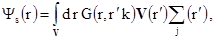                                      (1.32)

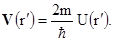                                                                  (1.33)

Используя разложение Вейля [13]

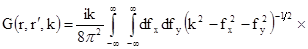            (1.34)

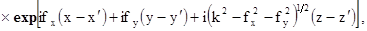
где

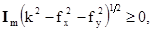                                                      (1.35)

и взяв преобразование Фурье от функции (1.32) по x и y, приходим к уравнению:

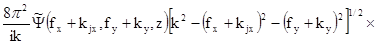
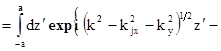                            (1.36)

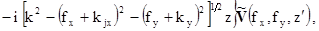
где 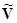 - Фурье-трансформанта функции  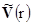по x и y; a обозначает носитель потенциала 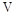 вдоль оси z. Система функци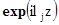й  при

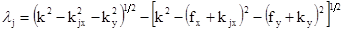 (1.37)

полна, если 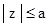. Однако в этом случае не существует функции, ортогональной ко всем функциям 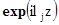 и отличной от нуля. Поэтому, если существует другой потенциал 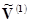, приводящий к той же самой левой части уравнения (1.36) при всех значениях j, то разность 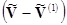 должна обращаться в нуль, что и доказывает требуемую единственность 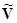, т.е.единственность решения обратной задачи рассеяния.

   Посредством ортонормирования системы функци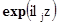й  при 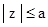 и вычисления различных коэффициентов Фурье определяется величина 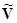. Потенциал однозначно определяется рассеянными полями вне объёма рассеивателя , созданными волнами (1.30), поскольку, если рассеяние на двух различных потенциалах приводит к одним и тем же рассеянным полям, то разность этих потенциалов, приводящая к нулевому рассеянному полю, должна быть равна нулю.

   Потенциал с конечным носителем также однозначно определяется рассеянными полями, образованными системой плоских волн с разными энергиями. Последний результат получается из рассмотрения

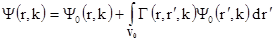                     (1.38)

интегрального уравнения рассеяния

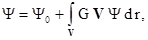                                                     (1.39)

где

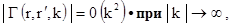                                  (1.40)

                    

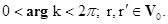
   Функция Грина 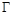 допускает разложение по собственным модам задачи рассеяния. Этот результат остаётся справедливым, если вместо потенциала рассеивающий объект характеризуется показателем преломления. Не существует доступного метода измерений в дальней зоне, позволяющего дать информацию, отличную от той, которую несут компоненты однородной плоской волны заданного поля. Отсюда следует заключение о возможности сверхразрешения по данным рассеяния в дальней зоне.

   При любом способе восстановления формы рассеивателя априорная информация о его общих геометрических свойствах позволяет однозначно решать обратную задачу рассеяния. При этом единственность и устойчивость решения обратной задачи рассеяния будет определяться приближением, используемым для описания волнового поля. Далее для решения проблем высокоинформативной радиолокации будут использоваться в существенной мере представления и методы современной нелинейной и когерентной оптики, радиооптические аналогиии. Интерес к радиооптическим аналогиям в последнее время усилился в связи с интенсивным развитием областей, стоящих на стыке радиофизики и оптики. Радиофизические и оптические явления в определенных идеализациях описываются сходными моделями и одинаковыми уравнениями.