ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ
ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА СТАТИСТИКИ
О Т Ч Е Т
о результатах выполнения
компьютерной лабораторной работы №1
«Автоматизированный априорный анализ
статистической совокупности в среде MS Excel»
Вариант №_10_
Выполнил: ст. III курса гр. дневная
3ФК1
Проверил:
Резяпова А.А.
Уфа, 2006г.
1. Постановка
задачи
При
проведении статистического наблюдения за деятельностью предприятий корпорации
получены выборочные данные по 32-м предприятиям, выпускающим однородную
продукцию (выборка 10%-ная,
механическая), о среднегодовой стоимости основных производственных фондов
и о выпуске продукции за год.
В
проводимом статистическом исследовании обследованные предприятия выступают как
единицы выборочной совокупности, а показатели Среднегодовая стоимость основных производственных фондов и Выпуск продукции – как изучаемые
признаки единиц.
Для
проведения автоматизированного статистического анализа совокупности выборочные
данные представлены в формате электронных таблиц процессора Excel в диапазоне
ячеек B4:C35 (Таблица 1)
Таблица 1
Исходные данные
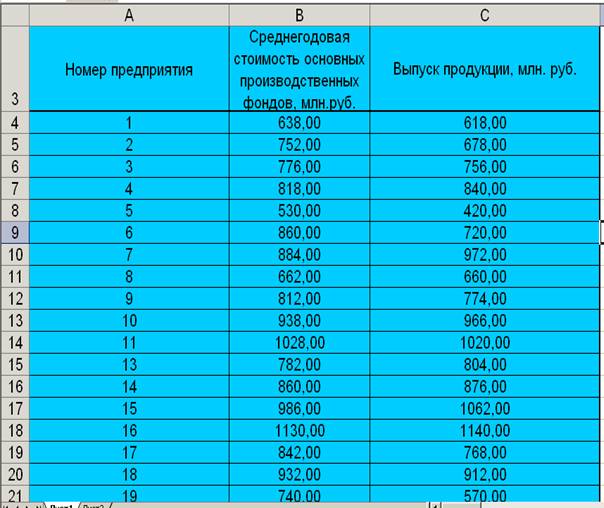
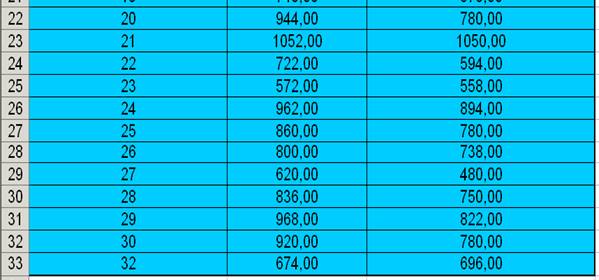
В
процессе исследования совокупности необходимо решить ряд статистических задач
для выборочной и генеральной
совокупностей.
Статистический анализ выборочной
совокупности
1. Выявить наличие среди
исходных данных резко выделяющихся значений признаков («выбросов» данных) с
целью исключения из выборки аномальных единиц наблюдения.
2. Рассчитать обобщающие
статистические показатели совокупности по изучаемым признакам: среднюю
арифметическую (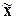 ), моду (Мо), медиану
(Ме), размах вариации (R), дисперсию(
), моду (Мо), медиану
(Ме), размах вариации (R), дисперсию(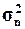 ),
средние отклонения – линейное (
),
средние отклонения – линейное (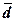 )
и квадратическое (σn), коэффициент вариации (Vσ), структурный коэффициент
асимметрии К.Пирсона (Asп).
)
и квадратическое (σn), коэффициент вариации (Vσ), структурный коэффициент
асимметрии К.Пирсона (Asп).
3. На основе рассчитанных
показателей в предположении, что распределения единиц по обоим признакам близки
к нормальному, оценить:
а) степень
колеблемости значений признаков в совокупности;
б) степень
однородности совокупности по изучаемым
признакам;
в)
устойчивость индивидуальных значений признаков;
г) количество попаданий
индивидуальных значений признаков в
диапазоны (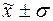 ), (
), (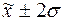 ), (
), (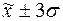 ).
).
4. Дать сравнительную
характеристику распределений единиц совокупности по двум изучаемым признакам на
основе анализа:
а) вариации
признаков;
б)
количественной однородности единиц;
в) надежности
(типичности) средних значений признаков;
г) симметричности
распределений в центральной части ряда.
5. Построить интервальный
вариационный ряд и гистограмму распределения единиц совокупности по признаку Среднегодовая стоимость основных
производственных фондов и установить характер (тип) этого распределения.
Рассчитать моду Мо полученного
интервального ряда и сравнить ее с показателем Мо несгруппированного ряда данных.
Статистический
анализ генеральной совокупности
1.
Рассчитать генеральную дисперсию 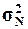 , генеральное среднее квадратическое
отклонение
, генеральное среднее квадратическое
отклонение 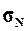 и ожидаемый размах
вариации признаков RN. Сопоставить значения этих показателей для
генеральной и выборочной дисперсий.
и ожидаемый размах
вариации признаков RN. Сопоставить значения этих показателей для
генеральной и выборочной дисперсий.
2.
Для изучаемых признаков рассчитать:
а) среднюю
ошибку выборки;
б)
предельные ошибки выборки для уровней надежности
P=0,683,
P=0,954, P=0,997 и границы, в которых будут
находиться средние значения признака
генеральной
совокупности
при заданных уровнях надежности.
3.
Рассчитать коэффициенты асимметрии As
и эксцесса Ek. На основе полученных
оценок сделать вывод о степени близости
распределения единиц генеральной совокупности к нормальному распределению.
Экономическое содержание задач статистического исследования
1.
Типичны ли образующие выборку предприятия по значениям
изучаемых экономических показателей?
· Построить точечный
график-диаграмму рассеяния значений показателей.
· Выделить область диаграммы,
отражающую группирование предприятий с близкими по значению показателями.
· Выявить предприятия с резко
выделяющимися характеристиками и исключить их из проводимого статистического
исследования вследствие нетипичности (аномальности) этих предприятий для
изучаемой совокупности.
Аномальные
значения показателей являются предметом отдельного исследования.
2.
Каковы наиболее характерные для предприятий значения
показателей среднегодовой стоимости основных фондов и выпуска продукции?
· Рассчитать среднюю
арифметическую значений каждого из показателей, а также среднее квадратическое
отклонение.
· Установить, какие предприятия входят в
диапазон (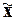
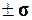 ), включающий предприятия с наиболее характерными значениями
показателей.
), включающий предприятия с наиболее характерными значениями
показателей.
3.
Насколько сильны различия в экономических
характеристиках предприятий выборочной совокупности? Можно ли утверждать, что
выборка сформирована из предприятий с достаточно близкими значениями по каждому
из показателей?
· Рассчитать коэффициенты
вариации, используя вычисленные в п. 2 значения 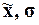 .
.
· Установить (по значению
коэффициента вариации), насколько предприятия однородны по изучаемым
экономическим характеристикам.
· Определить максимальное
расхождение в значениях показателей (размах вариации).
4.
Какова структура предприятий выборочной совокупности
по среднегодовой стоимости основных фондов? Каков удельный вес предприятий с
наибольшими, наименьшими и типичными значениями данного показатели? Какие именно
это предприятия?
· Произвести группировку
(построить ряд распределения) предприятий по стоимости основных фондов.
· Найти модальный интервал и
определить входящие в него предприятия (наиболее типичные).
· Установить, какие
предприятия входят в группы с наименьшей и наибольшей стоимостью основных
фондов.
· Определить удельный вес
предприятий модального интервала и интервалов с наибольшими и наименьшими
значениями показателя.
5.
Носит ли распределение предприятий по группам
закономерный характер и какие предприятия (с более высокой или более низкой
стоимостью основных фондов) преобладают в совокупности?
· Построить гистограмму ряда
распределения и визуально установить, имеется ли в распределении определенная
закономерность.
· В случае, если распределение
близко к нормальному, рассчитать показатель асимметрии, по знаку которого
определить, доминируют ли в совокупности предприятия с более высокой или с
более низкой стоимостью основных фондов.
6.
Каковы ожидаемые средние величины среднегодовой
стоимости основных фондов и выпуска продукции на предприятиях корпорации
в целом? Какое максимальное расхождение в значениях показателя можно
ожидать?
· Рассчитать предельную ошибку
средней для каждого из показателей.
· Определить границы, в
которых будут находиться средние значения показателей.
· Определить ожидаемый размах
вариации показателей.
2. Алгоритм выполнения всех заданий.
Распечатка рабочего файла с
результативными таблицами и графиками
Задание 1
Выявление и удаление из выборки аномальных
единиц наблюдения
Первичные данные выборочной совокупности могут
содержать аномальные значения изучаемых признаков. Задание 1 заключается в их
выявлении и исключении из дальнейшего рассмотрения с целью обеспечения
устойчивости данных статистического анализа.
Этап
1. Построение диаграммы рассеяния изучаемых признаков
1. Выделить мышью оба столбца
исходных данных в диапазоне B4:C35.
2. Вставка=>Диаграмма=>Точечная=>Готово.
В результате выполнения этих
действий на рабочем листе Excel появится диаграмма
рассеяния (Рис.1).
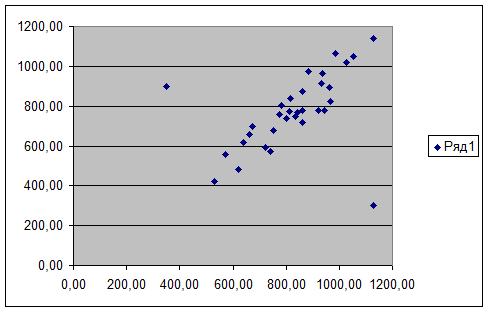
Рис.1. Аномальные значения
признаков на диаграмме рассеяния.
Этап 2. Визуальный анализ диаграммы рассеяния, выявление и фиксация
аномальных значений признаков, их удаление из первичных данных
1. Найти на графике точку,
соответствующую аномальному наблюдению. Если таких точек нет, то перейти к
действию 7, если есть - к действиям 2 - 6.
2. Подвести курсор к точке на
диаграмме рассеяния, соответствующей аномальному наблюдению. После
непродолжительного времени возле точки автоматически появится надпись,
содержащая значения признаков этого наблюдения в формате (X,Y).
3. В исходных данных визуально
(либо с помощью поисковых средств Excel) найти в табл.1 строку, соответствующую
выявленной аномальной единице наблюдения
(предприятию). Скопировать эту строку в табл.2.
4. Выделить мышью всю адресную
строку с данными, подлежащими удалению.
5. Правка=>Удалить.
6. Выполнять действия 1-5 до
полного удаления всех аномальных наблюдений.
7. Переместить диаграмму
рассеяния в область ячеек, начиная с ячейки F4.
|
|
Таблица 2
|
|
Аномальные единицы наблюдения
|
|
Номер
предприятия
|
Среднегодовая
стоимость основных производственных фондов, млн.руб.
|
Выпуск
продукции, млн. руб.
|
|
12
|
350,00
|
900,00
|
|
31
|
1130,00
|
300,00
|
Задание 2
Оценка
описательных статистических
параметров совокупности
Обобщающие
статистические показатели совокупности исчисляются на основе анализа
вариационных рядов распределения. Однако пакет Excel позволяет рассчитать
многие из этих показателей непосредственно по первичным данным наблюдения,
используя инструмент Описательная
статистика надстройки Пакет анализа,
а также статистические функции
инструмента Мастер функций.
Алгоритмы выполнения Задания
2
Выполнение задания включает три этапа:
1.Расчет описательных параметров
выборочной и генеральной совокупностей с использованием инструмента Описательная статистика.
2.Оценка предельных ошибок выборки для
различных уровней надежности в режиме Описательная
статистика.
3.Расчет описательных параметров
выборочной совокупности с использованием инструмента Мастер функций.
Этап 1. Расчет описательных параметров выборочной и
генеральной совокупностей с
использованием инструмента ОПИСАТЕЛЬНАЯ СТАТИСТИКА
1.Сервис=>Анализ данных=>Описательная
статистика=>OK;
2.Входной
интервал<=диапазон ячеек таблицы 3, Столбец 1 и Столбец 2;
3.Группирование =>по столбцам;
4.Итоговая статистика - Активизировать;
5.Уровень надежности - Активизировать;
6.Уровень надежности <= 95,4;
7.Выходной
интервал <= адрес ячейки
заголовка первого столбца
табл.3;
8.OK;
9.При появлении окна с сообщением "Выходной интервал накладывается на имеющиеся
данные" =>ОК.
В
результате указанных действий Excel
осуществляет вывод таблицы описательных статистик в заданный диапазон рабочего
файла.
|
|
|
Таблица
3
|
|
Описательные статистики
|
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
|
Столбец1
|
|
Столбец2
|
|
|
|
|
|
|
|
Среднее
|
830
|
Среднее
|
782,6
|
|
Стандартная
ошибка
|
26,49606347
|
Стандартная
ошибка
|
31,60752857
|
|
Медиана
|
839
|
Медиана
|
777
|
|
Мода
|
860
|
Мода
|
780
|
|
Стандартное
отклонение
|
145,1249165
|
Стандартное
отклонение
|
173,1215638
|
|
Дисперсия
выборки
|
21061,24138
|
Дисперсия
выборки
|
29971,07586
|
|
Эксцесс
|
-0,344943844
|
Эксцесс
|
-0,205332365
|
|
Асимметричность
|
-0,152503649
|
Асимметричность
|
0,042954448
|
|
Интервал
|
600
|
Интервал
|
720
|
|
Минимум
|
530
|
Минимум
|
420
|
|
Максимум
|
1130
|
Максимум
|
1140
|
|
Сумма
|
24900
|
Сумма
|
23478
|
|
Счет
|
30
|
Счет
|
30
|
|
Уровень
надежности(95,4%)
|
55,23931021
|
Уровень
надежности(95,4%)
|
65,89575382
|
|
|
|
|
Этап 2. Оценка предельных ошибок выборки для различных
уровней надежности в режиме Описательная статистика.
Алгоритм 2.1. Расчет
предельной ошибки выборки при P=0,683
1. Сервис =>Анализ данных =>Описательная статистика
=>OK;
2. Входной
интервал<= диапазон ячеек таблицы
4а, Столбец 1 и Столбец 2;
3. Итоговая
статистика – Снять флажок;
4. Уровень
надежности – Активизировать;
5. Уровень
надежности<= 68,3;
6. Выходной интервал <= адрес ячейки, заголовка
первого столбца табл.4а;
7. OK;
8. При
появлении окна с сообщением "Выходной
интервал накладывается
на имеющиеся данные" =>ОК.
Алгоритм 2.2. Расчет
предельной ошибки выборки при P=0,997
1. Сервис=>Анализ данных=>Описательная
статистика=>OK;
2. Входной
интервал<= диапазон ячеек таблицы
4б, Столбец 1 и Столбец 2;
3. Итоговая
статистика – Снять флажок;
4. Уровень
надежности – Активизировать;
5. Уровень
надежности <= 99,7;
6. Выходной
интервал <= адрес ячейки
заголовка первого столбца
табл.4б;
7. OK;
8. При появлении окна с сообщением "Выходной интервал накладывается на имеющиеся
данные" =>ОК.
В
результате работы алгоритмов 2.1 и 2.2 Excel выводит в соответствующие ячейки
табл.4 рабочего файла значения предельных ошибок выборки при P=0,683 и P=0,997.
|
|
|
Таблица
4а
|
|
Предельные ошибки выборки
|
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
|
Столбец1
|
|
Столбец2
|
|
|
|
|
|
|
Уровень
надежности(68,3%)
|
26,97843667
|
Уровень
надежности(68,3%)
|
32,18295837
|
|
|
|
|
|
|
|
|
|
|
|
Таблица
4б
|
|
Предельные ошибки выборки
|
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
|
Столбец1
|
|
Столбец2
|
|
|
|
|
|
|
Уровень
надежности(99,7%)
|
85,83139699
|
Уровень
надежности(99,7%)
|
102,3894865
|
|
|
|
|
Этап 3. Расчет описательных параметров выборочной
совокупности
с
использованием инструмента Мастер
функций
Алгоритм 3.1. Расчет
выборочного стандартного отклонения σn для признака
Среднегодовая стоимость основных
производственных фондов
1. Установить курсор в ячейку В83;
2. Вставка =>Функция;
3. Статистические
=>СТАНДОТКЛОНП=>ОК;
4. Число 1<=
диапазон ячеек табл.1, содержащих
значения первого признака.
Алгоритм 3.2. Расчет
выборочного стандартного отклонения σn для признака
Выпуск продукции
1. Установить курсор в ячейку D83;
2. Вставка =>Функция;
3. Статистические
=>СТАНДОТКЛОНП=>ОК;
4. Число 1<=
диапазон ячеек табл.1, содержащих
значения второго признака.
Алгоритм 3.3. Расчет
выборочной дисперсии σ2n для признака
Среднегодовая
стоимость основных производственных фондов
1. Установить курсор в ячейку В84;
2. Вставка =>Функция;
3. Статистические
=>ДИСПР=>ОК;
4. Число1<= диапазон ячеек табл.1, содержащий значения первого
признака.
Алгоритм 3.4. Расчет
выборочной дисперсии σ2n по признаку
Выпуск продукции
1. Установить курсор в ячейку D84;
2. Вставка =>Функция;
3. Статистические
=> ДИСПР=>ОК;
4. Число1<= диапазон ячеек табл.1, содержащих значения второго
признака.
Алгоритм 3.5. Расчет
выборочного среднего линейного отклонения 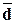 по
по
признаку Среднегодовая стоимость основных
производственных фондов
1. Установить курсор в ячейку В85;
2. Вставка =>Функция;
3. Статистические
=>СРОТКЛ=>ОК;
4. Число1<= диапазон ячеек табл.1, содержащих значения первого
признака.
Алгоритм 3.6. Расчет
выборочного среднего линейного отклонения 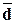 по
по
признаку Выпуск продукции
1. Установить курсор в ячейку D85;
2. Вставка =>Функция;
3. Статистические
=> СРОТКЛ =>ОК;
4. Число1<= диапазон ячеек табл.1, содержащих значения второго
признака.
Алгоритм 3.7. Расчет
коэффициента вариации 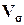 по признаку
по признаку
Среднегодовая стоимость основных
производственных фондов
1. Установить курсор в ячейку В86;
2. В активизированную ячейку ввести формулу =B83/B48*100.
Алгоритм 3.8. Расчет
коэффициента вариации 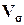 по признаку
по признаку
Выпуск продукции
1. Установить курсор в ячейку D86;
2. В активизированную ячейку ввести формулу =D83/D48*100.
Алгоритм 3.9. Расчет
выборочного коэффициента асимметрии Пирсона Asп по
признаку
Среднегодовая стоимость основных
производственных фондов
1. Установить курсор в ячейку В87;
2. В активизированную ячейку ввести формулу =(B48-B51)/B83.
Алгоритм 3.10. Расчет
выборочного коэффициента асимметрии Пирсона Asп по
признаку Выпуск продукции
1. Установить курсор в ячейку D87;
2. В активизированную ячейку ввести формулу =(D48-D51)/D83
В результате работы алгоритмов 3.1 - 3.10 Excel осуществляет вывод значений выборочных параметров σn, σ2n, 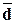 ,
, 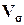 и Аsn в соответствующие ячейки рабочего листа Табл.5.
и Аsn в соответствующие ячейки рабочего листа Табл.5.
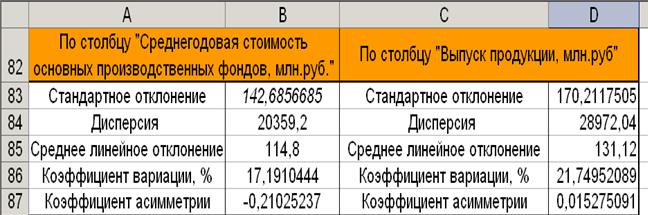
Таблица
5
Выборочные показатели
вариации и асимметрии
Задание 3
Построение и
графическое изображение интервального вариационного ряда распределения единиц
совокупности по признаку Среднегодовая стоимость основных производственных
фондов
Для того, чтобы выявить структуру
совокупности и тип закономерности распределения ее единиц по варьирующему
признаку, строят и анализируют интервальный
вариационный ряд распределения
и его гистограмму.
Выполнение Задания 3 заключается в решении
двух статистических задач:
1. Построение интервального
ряда распределения единиц выборочной совокупности по признаку Среднегодовая
стоимость основных производственных фондов.
2. Построение гистограммы и кумуляты сформированного
интервального ряда.
Алгоритмы выполнения Задания 3
Выполнение задания осуществляется в три
этапа:
1.
Построение
промежуточной таблицы.
2.
Генерация
выходной таблицы и графиков.
3.
Приведение
выходной таблицы и диаграммы к виду, принятому в статистике.
Этап 1. Построение
промежуточной таблицы.
Алгоритм 1.1. Расчет нижних
границ интервалов
1.
Сервис =>Анализ данных =>Гистограмма =>ОК;
2.
Входной интервал<= диапазон ячеек В4:В33;
!!! Внимание. Здесь возможен
ошибочный захват мышью
столбца второго признака. Необходимо
проконтролировать правильность задания входных данных!
3.
Интервал карманов оставить незаполненным;
4.
Выходной интервал <= адрес заголовка первого столбца первичной промежуточной
табл.6 ( А90 ).
5. OK;
Алгоритм 1.2. Переход от нижних границ к верхним
1. Выделить курсором верхнюю левую ячейку табл.6 и нажать
клавишу [Delete];
2. Ввести в ячейку с именем "Еще" значение хmax первого признака из табл.3-Описательные статистики.
|
Таблица 6
|
|
Таблица 6
|
|
Карман
|
Частота
|
Карман
|
Частота
|
|
530
|
1
|
|
1
|
|
650
|
3
|
650
|
3
|
|
770
|
5
|
770
|
5
|
|
890
|
11
|
890
|
11
|
|
1010
|
7
|
1010
|
7
|
|
Еще
|
3
|
1130
|
3
|
|
|
|
|
|
Рис. 2. Схема перехода от нижних границ интервалов к
верхним
Этап 2. Генерация выходной
таблицы и графиков
Алгоритм 2.1. Построение
выходной таблицы, столбиковой диаграммы и
кумуляты.
1.
Сервис=>Анализ
данных=>Гистограмма=>ОК;
2.
Входной интервал<= диапазон ячеек В4:В33;
!!!Внимание! Здесь возможен ошибочный
захват мышью столбца второго
признака. Необходимо проконтролировать правильность задания входных данных!
3.
Интервал карманов <= диапазон карманов итоговой промежуточной табл.6 с
верхними границами ( А92:А96);
4.
Выходной интервал <= адрес заголовка первого столбца выходной табл.7
( А101 );
5.
Интегральный процент - Активизировать;
6.
Вывод графика -
Активизировать;
7.
ОК;
8.
При появлении
сообщения о наложении данных - ОК.
|
|
Таблица 7
|
|
Интервальный ряд распределения предприятий
по стоимости основных производственных
фондов
|
|
Карман
|
Частота
|
Интегральный %
|
|
650
|
4
|
13,33%
|
|
770
|
5
|
30,00%
|
|
890
|
11
|
66,67%
|
|
1010
|
7
|
90,00%
|
|
1130
|
3
|
100,00%
|
|
Еще
|
0
|
100,00%
|
Этап 3. Приведение выходной таблицы и диаграммы к виду, принятому в
статистике.
Алгоритм 3.1. Преобразование
выходной таблицы в результативную.
1. Заменить названия столбцов выходной табл.7;
2. Строки первого столбца привести к виду «нижняя
граница интервала - верхняя граница интервала», учитывая
совпадение верхних границ предыдущего интервала с нижней границей последующего
интервала;
3. Строку с именем «Еще» выделить мышью и очистить,
нажав клавишу [Delete];
4. Добавить и заполнить строку с именем «Итого».
|
|
Таблица 7
|
|
|
|
|
Интервальный ряд распределения предприятий
по стоимости основных производственных
фондов
|
|
Группы предприятий по среднегодовой
стоимости основных фондов
|
Число предприятий в группе
|
Накопленная частость группы, %
|
|
530-650
|
4
|
13,33%
|
|
650-770
|
5
|
30,00%
|
|
770-890
|
11
|
66,67%
|
|
890-1010
|
7
|
90,00%
|
|
1010-1130
|
3
|
100,00%
|
|
итого
|
30
|
|
Алгоритм 3.2. Преобразование
столбиковой диаграммы в гистограмму.
1. Осуществив «захват мышью», переместить график,
расположив его вслед за табл.7;
2. Исключить зазоры, выполнив следующие действия:
2.1. Нажать правую кнопку мыши на одном
из столбиков диаграммы.;
2.2. Формат
рядов данных=>Параметры;
2.3. Ширина
зазора<= 0;
2.4. ОК;
3. Используя "захват мышью" за угол поля
графика, установить соотношение ширины и высоты
фигуры гистограммы в пропорции 1 : 0,62.
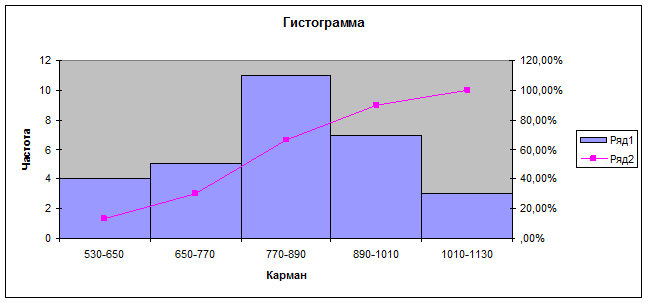
Рис. 3. Гистограмма и кумулята
3. Выводы о статистических свойствах
изучаемой совокупности
Статистический анализ выборочной
совокупности
Задача 1. Количество аномальных единиц 2шт, Таблица 2.
Задача 2.
Таблица 8
Описательные статистики выборочной
совокупности
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
|
Столбец1
|
|
Столбец2
|
|
|
|
|
|
|
|
Среднее
|
830
|
Среднее
|
782,6
|
|
Стандартная
ошибка
|
26,49606347
|
Стандартная
ошибка
|
31,60752857
|
|
Медиана
|
839
|
Медиана
|
777
|
|
Мода
|
860
|
Мода
|
780
|
|
Стандартное
отклонение
|
145,1249165
|
Стандартное
отклонение
|
173,1215638
|
|
Дисперсия
выборки
|
21061,24138
|
Дисперсия
выборки
|
29971,07586
|
|
Эксцесс
|
-0,344943844
|
Эксцесс
|
-0,205332365
|
|
Асимметричность
|
-0,152503649
|
Асимметричность
|
0,042954448
|
|
Интервал
|
600
|
Интервал
|
720
|
|
Минимум
|
530
|
Минимум
|
420
|
|
Максимум
|
1130
|
Максимум
|
1140
|
|
Сумма
|
24900
|
Сумма
|
23478
|
|
Счет
|
30
|
Счет
|
30
|
|
Уровень
надежности(95,4%)
|
55,23931021
|
Уровень
надежности(95,4%)
|
65,89575382
|
|
Стандартное
отклонение
|
142,6856685
|
Стандартное
отклонение
|
170,2117505
|
|
Дисперсия
|
20359,2
|
Дисперсия
|
28972,04
|
|
Среднее
линейное отклонение
|
114,8
|
Среднее
линейное отклонение
|
131,12
|
|
Коэффициент
вариации, %
|
17,1910444
|
Коэффициент
вариации, %
|
21,74952089
|
|
Коэффициент
асимметрии
|
-0,21025237
|
Коэффициент
асимметрии
|
0,015275091
|
Задача 3.
а) степень колеблемости значений признаков в
совокупности:
-для первого признака,
коэффициент вариации равен 17,1910444, т.к
0%<17.19≤40%,
то колеблемость
незначительна;
- для второго признака,
коэффициент вариации равен 21,74952089, т.к
0%<21.75≤40%,
то колеблемость
незначительна.
б)степень однородности
совокупности по изучаемым признакам:
Для нормальных и близких к
нормальному распределений показатель Vσ служит
индикатором однородности совокупности: принято считать, что при выполнимости
неравенства
Vσ ≤
33%, 17,19 ≤ 33% и 21,75 ≤
33%
совокупность является
количественно однородной по данным признакам.
в)
устойчивость индивидуальных значений признаков:
Сопоставление средних отклонений –
квадратического s и линейного 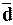 позволяет сделать
вывод об устойчивости индивидуальных значений признака, т.е. об
отсутствии среди них «аномальных» вариантов значений.
позволяет сделать
вывод об устойчивости индивидуальных значений признака, т.е. об
отсутствии среди них «аномальных» вариантов значений.
В условиях симметричного и нормального, а
также близких к ним распределений между показателями s и 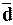 имеют место равенства
имеют место равенства
s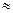 1,25
1,25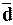 ,
, 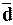
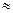 0,8s,
0,8s,
поэтому отношение показателей
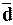 и s может
служить индикатором устойчивости данных: если
и s может
служить индикатором устойчивости данных: если
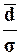 >0,8,
>0,8,
то значения признака
неустойчивы, в них имеются «аномальные» выбросы.
σ ≈ 1,25*114,8 ≈
142,68; 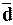 ≈ 0,8*142,68
≈ 114,8 ;
≈ 0,8*142,68
≈ 114,8 ;
т.к. неравенство 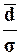 >0,8 не выполняется, то первый признак устойчив.
>0,8 не выполняется, то первый признак устойчив.
σ ≈ 1,25*131,12 ≈
163,9; 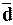 ≈ 0,8*170,2
≈ 136,1;
≈ 0,8*170,2
≈ 136,1;
т.к. неравенство 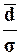 >0,8 не выполняется, то второй признак устойчив.
>0,8 не выполняется, то второй признак устойчив.
г) количество попаданий
индивидуальных значений признаков в диапазоны
(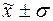 ), (
), (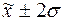 ), (
), (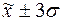 ):
):
По
значениям показателей 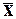 и s можно определить границы диапазонов рассеяния значений
признака относительно средней
и s можно определить границы диапазонов рассеяния значений
признака относительно средней 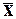 , т.е. установить, какая доля значений признака попадает в
тот или иной диапазон отклонений от
, т.е. установить, какая доля значений признака попадает в
тот или иной диапазон отклонений от 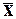 .
.
В
нормально
распределенных и близких к ним рядах вероятностные оценки диапазонов
рассеяния значений признака таковы:
68,3% войдет в диапазон (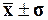 );
);
95,4% попадет в диапазон (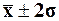 );
);
99,7%
появится в диапазон (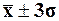 )
)
Это
соотношение известно как правило
«трех сигм».
Таблица 9
Распределение значений признака по диапазонам
рассеяния признака относительно 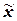
|
Границы диапазонов
|
Количество значений xi, находящихся в диапазоне
|
|
Первый признак
|
Второй признак
|
Первый признак
|
Второй признак
|
|
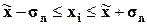
|
687 ≤ х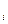 ≤ 973 ≤ 973
|
612
≤ х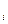 ≤ 953 ≤ 953
|
20
|
20
|
|
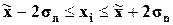
|
545 ≤ х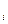 ≤ 1115 ≤ 1115
|
442
≤ х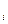 ≤ 1123 ≤ 1123
|
28
|
28
|
|
|
402 ≤ х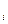 ≤ 1258 ≤ 1258
|
272
≤ х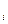 ≤ 1293 ≤ 1293
|
30
|
30
|
Процентное соотношение рассеяния значений признака по трем
диапазонам составляет:
66,6% войдет в диапазон (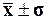 );
);
93,3% попадет в диапазон (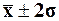 );
);
100%
появится в диапазон (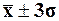 )
)
что соответствует правилу «трех сигм».
Задача 4.
а) по
вариации признаков:
Показатели вариации признака описывают степень рассеяния
вариантов значений признака относительно своего центра 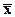 (или Ме). Различают показатели размера и
интенсивности вариации.
(или Ме). Различают показатели размера и
интенсивности вариации.
В статистической практике для оценки
вариации наиболее широко применяются показатели размера вариации s2, s и показатель интенсивности вариации Vs.
Показатели s2, s, основанные на учете отклонений (xi-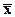 ) индивидуальных значений признака xi от
средней арифметической
) индивидуальных значений признака xi от
средней арифметической 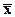 , являются обобщающими
характеристиками различия в значениях признака.
, являются обобщающими
характеристиками различия в значениях признака.
Дисперсия s2 оценивает средний квадрат отклонений (xi
-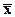 ). Величина s очень чутко реагирует на вариацию признака (за счет возведения
отклонений в квадрат) и органически вписывается в аппарат математической
статистики (дисперсионный, корреляционный анализ и др.). На расчете дисперсии
основаны многие статистические показатели.
). Величина s очень чутко реагирует на вариацию признака (за счет возведения
отклонений в квадрат) и органически вписывается в аппарат математической
статистики (дисперсионный, корреляционный анализ и др.). На расчете дисперсии
основаны многие статистические показатели.
Среднее
квадратическое отклонение s показывает, на сколько в среднем отклоняются индивидуальные значения признака xi от их средней величины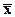 .
.
В данном случае по первому
признаку среднее квадратическое отклонение равно 142,69, а по второму равно
170,21.
Размерность отклонения s совпадает с размерностью самого признака, поэтому
этот показатель экономически хорошо интерпретируется. Отклонения, выраженные в s, принято считать стандартными.
Интенсивность вариации обычно измеряют коэффициентом вариации Vs , который выражается в процентах и вычисляется по
формуле
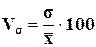
Величина Vs оценивает интенсивность колебаний вариантов
относительно их средней величины. Принята следующая оценочная шкала колеблемости признака:
0%<Vs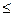 40% - колеблемость незначительная;
40% - колеблемость незначительная;
40%< Vs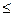 60% - колеблемость средняя (умеренная);
60% - колеблемость средняя (умеренная);
Vs>60% - колеблемость значительная.
В
нашем случае:
-для
первого признака, коэффициент вариации равен 17,1910444, т.к
0%<17.19≤40%,
то колеблемость
незначительна;
- для второго признака,
коэффициент вариации равен 21,74952089, т.к
0%<21.75≤40%,
то колеблемость незначительна.
б) по количественной однородности
единиц:
Количественная однородность совокупности –
это близость числовых значений признаков, определяющих качественное содержание
совокупности.
Однородность статистической совокупности
означает, что все ее единицы обладают сходством по некоторому кругу признаков,
обусловливающих качественную определенность совокупности, а количественные
значения этих признаков оказываются близкими друг к другу.
в)
по надежности (типичности) средних значений признаков:
Для оценка надежности (типичности) средней
величины 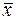 можно воспользоваться
значением показателя вариации, Vs. Если его значение невелико
(в нашем случае оно меньше 40%), то индивидуальные значения признака xi мало отличаются друг от друга, единицы наблюдения количественно однородны
и, следовательно, средняя арифметическая величина
можно воспользоваться
значением показателя вариации, Vs. Если его значение невелико
(в нашем случае оно меньше 40%), то индивидуальные значения признака xi мало отличаются друг от друга, единицы наблюдения количественно однородны
и, следовательно, средняя арифметическая величина 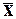 является надежной характеристикой
данной совокупности.
является надежной характеристикой
данной совокупности.
г)
по симметричности распределений в центральной части ряда:
Показатели асимметрии оценивают смещение ряда распределения влево или
вправо по отношению к оси симметрии нормального распределения.
В симметричном распределении максимальная
ордината прямой располагается точно в середине кривой , а соответствующие ей
характеристики центра распределения совпадают:
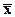 =Mo=Me
=Mo=Me
В случае асимметричного распределения
вершина кривой находится не в середине, а сдвинута либо влево, либо вправо.
Если вершина сдвинута влево, то правая
часть кривой оказывается длиннее левой, т.е. имеет место правосторонняя
асимметрия, характеризующаяся неравенством
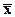 >Me>Mo,
>Me>Mo,
что означает преимущественное
появление в распределении более высоких значений признака.
Этому неравенству соответствует второй
признак (Табл. 8).
Если же вершина кривой сдвинута вправо и левая
часть оказывается длиннее правой, то асимметрия левосторонняя
, для которой справедливо неравенство
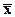 <Me<Mo,
<Me<Mo,
означающее, что в распределении
чаще встречаются более низкие значения признака.
Этому неравенству соответствует первый
признак (Табл. 8)
Для оценки асимметричности распределения
в этом центральном диапазоне служит коэффициент К.Пирсона.
При правосторонней асимметрии Asп>0, при левосторонней Asп<0. Если Asп=0, вариационный ряд
симметричен.
В нашем случае первый признак меньше нуля,
значит левосторонняя асимметрия, а второй признак больше нуля, значит
правосторонняя асимметрия (Табл.8).
Задача 5.
Интервальный вариационный ряд представляет признак в виде
упорядоченного набора интервалов значений признака с указанием для каждого интервала
его частоты, фиксирующей число попаданий значений признака в данный интервал.
Интервальный ряд распределения предприятий
по Стоимости основных производственных
фондов представлен в Таблице 7.
Гистограмма распределения единиц
совокупности по признаку Среднегодовая
стоимость основных производственных фондов рис.3.
Мы определили (Задача 4, п. г) ), что вершина кривой сдвинута вправо и левая часть
оказывается длиннее правой, то асимметрия левосторонняя ,
для которой справедливо неравенство
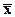 <Me<Mo,
<Me<Mo,
означающее, что в распределении
чаще встречаются более низкие значения признака.
Показатель эксцесса
характеризует крутизну кривой распределения - ее заостренность
или пологость
по сравнению с нормальной кривой. Т.к. коэффициент эксцесса Ek меньше
нуля, то наша кривая с плосковершинным распределением.
Гистограмма имеет одновершинную
форму, есть основания предполагать, что выборка является однородной
по данному признаку. Как мы определили (в Задаче 3, п. б) ) совокупность является количественно однородной по
данному признаку.
Т.к. асимметрия небольшая, то относится к
нормальному типу.
Для полученного интервального ряда значение моды Мо
рассчитывается по формуле:
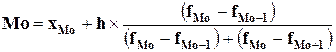 ,
,
где: хМо – нижняя граница модального интервала;
h – величина модального интервала;
fMo – частота модального интервала;
fMo-1 – частота интервала, предшествующего модальному;
fMo+1 – частота интервала, следующего за модальным.
Мо = 530 + 600 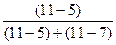 = 890
= 890
Это означает, что наиболее часто
встречаемая величина признаков данной совокупности равна 890.
Анализ генеральной совокупности
Задача 1.
Таблица 10
Описательные статистики генеральной
совокупности
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
|
Стандартное
отклонение
|
145,1249165
|
Стандартное
отклонение
|
173,1215638
|
|
Дисперсия
выборки
|
21061,24138
|
Дисперсия
выборки
|
29971,07586
|
|
Эксцесс
|
-0,344943844
|
Эксцесс
|
-0,205332365
|
|
Асимметричность
|
-0,152503649
|
Асимметричность
|
0,042954448
|
В
математической статистике доказано, что при малом числе наблюдений (особенно
при n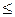 40-50) для
вычисления генеральной дисперсии σ2N по выборочной дисперсии σ2n следует
использовать формулу
40-50) для
вычисления генеральной дисперсии σ2N по выборочной дисперсии σ2n следует
использовать формулу
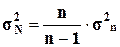
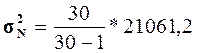 = 21693,36
= 21693,36 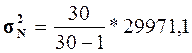 = 30870,2
= 30870,2
Степень расхождения между 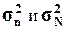 незначительна.
незначительна.
Для
нормального распределения справедливо равенство
R=6s
R = 6 * 142.68 = 856.08
R = 6 * 170.2 = 1021.2
Задание 2.
а) рассчитать среднюю ошибку выборки;
Средние ошибки выборки рассчитаны и
приведены в табл.3 (параметр Стандартная
ошибка).
Для первого признака она равна 26,496, для
второго 31,608.
б) рассчитать предельные ошибки выборки для
уровней надежности P=0,683, P=0,954, P=0,997 и границы, в которых будут
находиться средние значения признака генеральной совокупности при заданных
уровнях надежности.
Таблица 11
Предельные ошибки
выборки и ожидаемые границы
для генеральных средних
|
Доверительная
вероятность
Р
|
Коэффициент
доверия
t
|
Предельные ошибки
выборки
|
Ожидаемые границы
для
средних 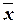
|
|
для первого
признака
|
для второго
признака
|
для первого
признака
|
для второго
признака
|
|
0,683
|
1
|
26,97843667
|
32,18295837
|
803,504≤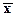 ≤ 856,496 ≤ 856,496
|
750,99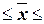 814,2 814,2
|
|
0,954
|
2
|
55,23931021
|
65,89575382
|
777,0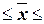 882,992 882,992
|
719,384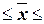 845,82 845,82
|
|
0,997
|
3
|
85,83139699
|
102,3894865
|
750,512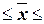 909,49 909,49
|
687,78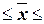 877,42 877,42
|
В математической статистике доказано, что
предельная ошибка выборки 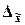 кратна средней
ошибке
кратна средней
ошибке 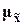 с
коэффициентом кратности t, зависящим
от значения доверительной вероятности P:
с
коэффициентом кратности t, зависящим
от значения доверительной вероятности P:
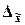 =
=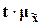
Величина коэффициента t (называемого также
коэффициентом
доверия) является нормированным отклонением.
Предельная ошибка выборки 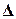 позволяет
определить предельные значения показателей генеральной совокупности и их доверительные
интервалы. Для генеральной средней предельные значения и доверительные
интервалы определяются выражениями:
позволяет
определить предельные значения показателей генеральной совокупности и их доверительные
интервалы. Для генеральной средней предельные значения и доверительные
интервалы определяются выражениями:
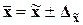 ,
,
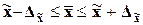
Рассмотрим для примера первый признак с доверительной вероятностью
0,683:
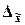 = 1 * 26,496 =
26,496.
= 1 * 26,496 =
26,496.
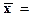 830±26,496
830±26,496
803,504≤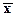 ≤856,496
≤856,496
Задача 3.
Значения коэффициентов асимметрии As и эксцесса Ek имеются в табл.10.
Распределение единиц выборочной
совокупности близко к нормальному, выборка является репрезентативной (значение
показателей σN2 и σn2 расходятся
незначительно) и при этом коэффициенты AsN, EkN указывают на небольшую или умеренную величину
асимметрии и эксцесса соответственно, то есть основание полагать, что
распределение единиц генеральной совокупности по изучаемому признаку будет
близко к нормальному