Содержание
ЗАДАЧА № 1. 3
ЗАДАЧА № 2. 6
ЗАДАЧА № 3: 12
Список литературы.. 16
ЗАДАЧА
№ 1
УСЛОВИЕ
ЗАДАЧИ:
Фирма
осуществляет производство и продажу товара через сеть фирменных магазинов.
Данные о цене товара и объеме проданных
товаров в среднем за сутки в одном из географических сегментов рынка приведены
в таблице 1.
Таблица
1
Данные
о цене и объеме проданных товаров в среднем за сутки
|
Цена товара, тыс. руб. (х)
|
3,00
|
3,05
|
3,10
|
3,15
|
3,20
|
3,25
|
3,30
|
3,35
|
3,40
|
3,45
|
3,50
|
|
Объем продажи товара,шт
(у)
|
48
|
46
|
41
|
39
|
36
|
31
|
27
|
26
|
24
|
26
|
22
|
НАЙТИ:
1) проанализировать
существующую зависимость между объемом продажи товара и уровнем его цены;
2) определить коэффициент
эластичности между ценой товара и объемом его продажи;
3) определить тесноту связи
между ценой и объемом продажи товара.
РЕШЕНИЕ:
1) На основании данных таблицы
1 графически изобразим объем продажи товара на рисунке 1.
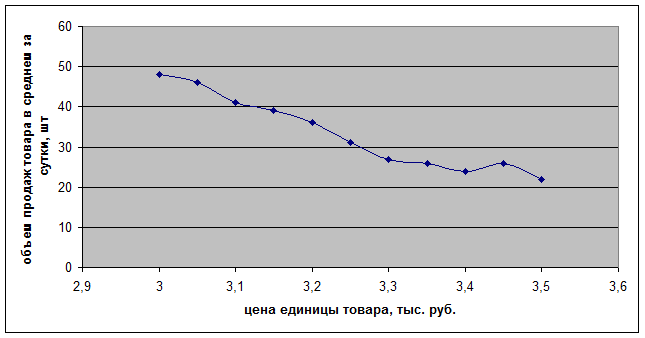
Рис. 1. Графическая
взаимосвязь между ценой товара и объемом его продажи
Рисунок 1 показывает, что для зависимости между ценой
продажи товара и объемами продажи может быть использовано уравнение прямой
линии:
у(х) = а0 +
а1 х, (1)
Для расчета значений а0 и а1 составим
вспомогательную таблицу 2.
Таблица 2
Вспомогательная таблица для
расчета значений а0 и а1
|
№ п/п
|
Цена единицы товара, тыс. руб. (х)
|
Общий объем продажи за сутки, ед.
(у)
|
ху
|
х2
|
у2
|
у(х)
|
|
1
|
3,0
|
48
|
144
|
9
|
2304
|
47,5
|
|
2
|
3,05
|
46
|
140
|
9,3
|
2116
|
44,1
|
|
3
|
3,1
|
41
|
127
|
9,6
|
1681
|
40,7
|
|
4
|
3,15
|
39
|
123
|
9,9
|
1521
|
37,3
|
|
5
|
3,2
|
36
|
115
|
10,2
|
1296
|
33,9
|
|
6
|
3,25
|
31
|
101
|
1,5
|
961
|
30,5
|
|
7
|
3,3
|
27
|
89,1
|
10,8
|
729
|
27,1
|
|
8
|
3,35
|
26
|
87,1
|
11,2
|
676
|
23,7
|
|
9
|
3,4
|
24
|
81,6
|
11,5
|
576
|
20,3
|
|
10
|
3,45
|
26
|
89,7
|
11,9
|
676
|
16,9
|
|
11
|
3,5
|
22
|
77
|
12.2
|
484
|
13,5
|
|
итого
|
35,75
|
366
|
1175
|
116,4
|
13020
|
|
|
среднее
|
3,25
|
30,5
|
|
-
|
2304
|
|
Значение коэффициента а1 определяется по формуле
(2):
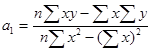 , (2)
, (2)
Используя данные таблицы 2, определяем:
а1 = (11* 1175 –
35,75 * 366) : ( 11* 116,4 – 35,75*35,75)
= (12925 – 13084,5) : (1280,4- 1278,06) = -159,5 : 2,34 = -68
Итого: а1 = - 68
Это число показывает теоретическую величину падения объема
продаж при увеличении цены на единицу стоимости.
Тогда коэффициент а0 можно для средних значений
можно определить по формуле (3):
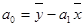 , (3)
, (3)
Используя данные таблицы 2, рассчитываем:
а0 = 30,5 - (-68)
* 3,25 = 251,5 ед.
Это число показывает теоретически возможный объем продаж при
минимальной цене.
Тогда теоретическое уравнение зависимости объема продаж от
цены примет вид:
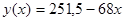
Расчет значений у(х) приведен в таблице 2 в графе 7
То есть теоретическая зависимость между объемом продаж и
ценой товара примет вид:
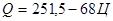
2) Коэффициент эластичности
рассчитывается по формуле (4):
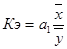 , (4)
, (4)
Таким образом, коэффициент
эластичности равен:
Кэ = - 68 * 3,25 : 30,5 = -7,25
Это число показывает процент изменения объема продаж при
изменении цены на 1 %.
3) Теснота связи между
показателями цены и объема продаж рассчитывается по формуле (5):
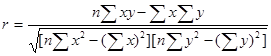 , (5)
, (5)
В нашем примере r = ( 11* 1175-35,75*366) : (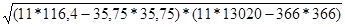 = - 159,5 : 149, 1 = -
1,07
= - 159,5 : 149, 1 = -
1,07
Так как значение r близко к – 1, следовательно, связь между ценой и объемом
продажи сильная.
ВЫВОДЫ:
1) спрос эластичен. Коэффициент
эластичности больше 1 и равен 7,25
2) При таком спросе политика
постоянного увеличения цены нецелесообразна. Необходимо определить оптимальную
цену с учетом изменения спроса на товар фирмы.
ЗАДАЧА
№ 2
УСЛОВИЕ ЗАДАЧИ:
Для оперативного регулирования цены с учетом установленной
эластичности спроса проанализировать затраты на производство и обращение товара на основании следующих
данных, представленных в таблице 3 и 5.
НАЙТИ:
1) разделить суммарные издержки
при использовании таблицы 3 производства, используя метод «максимальной и
минимальной точки»;
2) разделить суммарные издержки
обращения товара с помощью метода наименьших квадратов;
3) составить методическую
модель валовых издержек производства и обращения товара.
РЕШЕНИЕ:
1) Метод максимальной и
минимальной точки.
Пусть фирма осуществляет
производство товара. Исходные данные об объеме производства и суммарных
затратах в среднем за сутки приведены в таблице 3
Таблица 3
Данные об объеме
производства и суммарных затрат на производство в среднем за сутки
|
Месяц
|
Объем производства в среднем за сутки, штук
|
Расходы производства в среднем за сутки, тыс. руб.
|
TC (Q)
|
Отклонение
|
|
1
|
205
|
2480
|
2434,6
|
45,4
|
|
2
|
175
|
2385
|
2385,4
|
-0,4
|
|
3
|
210
|
2430
|
2442,8
|
-12,8
|
|
4
|
205
|
2400
|
2434,6
|
-34,6
|
|
5
|
180
|
2360
|
2393,6
|
-33,6
|
|
6
|
185
|
2370
|
2401,8
|
-31,8
|
|
7
|
230
|
2500
|
2475,6
|
24,4
|
|
8
|
250
|
2550
|
2508,4
|
41,6
|
|
9
|
260
|
2535
|
2524,8
|
10,2
|
|
10
|
305
|
2600
|
2598,6
|
1,4
|
|
11
|
315
|
2615
|
2615
|
0
|
|
12
|
210
|
2460
|
2442,8
|
17,2
|
Из всей совокупности данных выбираем два периода с
наименьшим и наибольшим объемом производства. Из таблицы 3 видно, что
наибольший объем производства в ноябре
составил 315 шт. Наименьший объем производства в январе – 175 шт.
Для расчета постоянных и переменных издержек составляем
вспомогательную таблицу 4.
Таблица 4
Вспомогательная таблица для
расчета постоянных и переменных затрат
|
Показатель
|
Объем производства
|
Разность между максимальными и минимальными
величинами
|
|
максимальный
|
минимальный
|
|
Уровень производства в среднем за сутки, штук (Q)
% (Q%)
|
315
100 %
|
175
55,56 %
|
140
44,44
|
|
Расходы производства в среднем за сутки, тыс. руб.
(ТС)
|
2615
|
2385
|
230
|
Определим ставку переменных издержек (средние переменные
расходы в себестоимости единицы продукции) по следующей формуле (6):
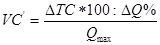 , (6)
, (6)
где VC’ – ставка переменных издержек;
∆ ТС – разность между максимальными и минимальными
величинами, равная 230 тыс. руб.
∆ Q% - разность между
максимальными и минимальными величинами, равная 44,44 %
Qмах – максимальный объем производства в среднем за сутки,
равный 315 шт.
По формуле (6) рассчитаем ставку переменных издержек:
VC’ = 230 * 100 : 44,44 : 315 = 1,64 (тыс. руб. \
шт.)
Общая сумма постоянных издержек (FC’) определяется по формуле (7):
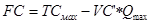 (7)
(7)
где ТСмах – суммарные (валовые) издержки, максимальному уровню производства,
равные 2615 тыс. руб.
Определим общую сумму постоянных издержек по формуле (7):
FC
= 2615 – 1.64 * 315 = 2098,4 ( тыс. руб.)
Таким образом, валовые издержки производства (ТС) могут быть
рассчитаны по формуле (8):
ТС =
FC + VC’ * Q, (8)
где Q – объем производства товара, штук.
ТС = 2098,4 + 1,64 * Q
Значение функции
представлено в 4 столбце таблицы 3.
2) Метод наименьших квадратов
Этот метод
позволяет более точно определить состав общих затрат и содержание в них
постоянной и переменной составляющих.
Фирма реализует товар на рынке. Исходные
данные по объему реализации в среднем за сутки (шт.) и валовых затрат обращения
в среднем за сутки (тыс. руб.) приведены в таблице 5
Таблица
5
Исходные
данные по объему реализации и затрат обращения в среднем за сутки
|
Месяц
|
Объем реализации в среднем за сутки, штук
|
Затраты обращения в среднем за сутки, тыс. руб.
|
TC (Q)
|
Отклонение
|
|
1
|
160
|
1155
|
1136,3
|
18,68
|
|
2
|
150
|
1135
|
1125,4
|
9,65
|
|
3
|
170
|
1145
|
1147,3
|
-2,29
|
|
4
|
240
|
1190
|
1224,1
|
-34,08
|
|
5
|
170
|
1140
|
1147,3
|
-7,29
|
|
6
|
210
|
1200
|
1191,2
|
8,83
|
|
7
|
270
|
1300
|
1257
|
43,01
|
|
8
|
260
|
1225
|
1246
|
-21,02
|
|
9
|
280
|
1300
|
1268
|
32,04
|
|
10
|
225
|
1195
|
1207,6
|
-12,63
|
|
11
|
260
|
1230
|
1246
|
-16,02
|
|
12
|
250
|
1220
|
1235,1
|
-15,05
|
Согласно данному
методу рассчитывают коэффициенты а и в в уравнении прямой
у = а + в * х, (9)
где у – общие (валовые) издержки;
а – уровень постоянных издержек;
в – ставка переменных издержек обращения в
расчете на единицу товара;
х – объем реализации, единиц.
Ставка переменных издержек в
определяется по формуле (10):
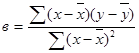 , (10)
, (10)
Для расчета величины в составляем вспомогательную таблицу 6
Таблица 6
Вспомогательная таблица для
расчета величины в
|
Месяц
|
Объем реализации (х)
|
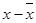
|
Суммарные издержки (у)
|
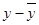
|
(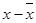 )2 )2
|
(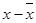 ) )
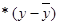
|
|
1
|
160
|
-60
|
1155
|
-48
|
3650
|
2895
|
|
2
|
150
|
-70
|
1135
|
-68
|
4959
|
4782
|
|
3
|
170
|
-50
|
1145
|
-58
|
2542
|
2920
|
|
4
|
240
|
20
|
1190
|
-13
|
384
|
-253
|
|
5
|
170
|
-50
|
1140
|
-63
|
2542
|
3172
|
|
6
|
210
|
-10
|
1200
|
-3
|
109
|
30
|
|
7
|
270
|
50
|
1300
|
97
|
2459
|
4814
|
|
8
|
260
|
40
|
1225
|
22
|
1567
|
874
|
|
9
|
280
|
60
|
1300
|
97
|
3550
|
5785
|
|
10
|
225
|
5
|
1195
|
-8
|
21
|
-36
|
|
11
|
260
|
40
|
1230
|
27
|
1567
|
1072
|
|
12
|
250
|
30
|
1220
|
17
|
875
|
505
|
|
итого
|
2645
|
0
|
14435
|
0
|
24223
|
26560
|
|
среднее
|
220
|
|
1203
|
|
|
|
Тогда, используя формулу (10) и данные таблицы 6, определяем
ставку переменных издержек:
в = 26560 : 24223 = 1,097
То есть, VC’
= 1,097 Тогда переменные издержки на
среднесуточный объем продаж (VC) составят:
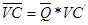 , (11)
, (11)
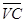 = 220 * 1,097 =
242.2 (тыс. руб.)
= 220 * 1,097 =
242.2 (тыс. руб.)
Постоянные издержки (FC) составляют:
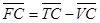 , (12)
, (12)
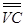 = 1203 – 242,2 =
960,8 (тыс. руб.)
= 1203 – 242,2 =
960,8 (тыс. руб.)
Таким образом, валовые издержки обращения могут быть
рассчитаны по формуле:
ТС (Q) = 960,8 + 1,097 Q (13)
где Q- объем реализации товара, штук
В столбце 4 таблицы 5 отражено значение ТС и отклонение.
Используя результаты предыдущей задачи определяем, что
постоянные издержки на производство и реализацию равны:
2098,4 + 960,8 = 3059,2 (тыс. руб.)
А удельные переменные издержки составили:
1,64 + 1,097 = 2,737 тыс. руб.\шт.
Таким образом, валовые издержки производства и обращения
могут быть рассчитаны по формуле (14):
ТС
= 3059,2 + 2,737 * Q (14)
ЗАДАЧА
№ 3:
Используя результаты,
полученные в задачах № 1 и № 2 определить:
1) оптимальный уровень цены с
учетом достижения максимальной прибыли (валовой маржи), предварительно
разработав экономико- математическую модель задачи;
2) объем производства и
продажи, обеспечивающий прибыль, равную 50 тыс. рублей в день при
складывающихся рыночных условиях;
3) оптимальный уровень цены,
обеспечивающий уровень прибыли, равный 50 тыс. рублей в день при уровне
производства и реализации равном 3000 и более штук.
РЕШЕНИЕ:
Используя результаты предыдущих задач:
1) полученную зависимость
объема реализации от цены:
Q = 251,5
- 68 Ц
где Q – среднесуточная продажа;
Ц – цена единицы товара, тыс. руб.
2) постоянные издержки на производство и обращение – 3059,2 тыс.
руб.
3) удельные переменные издержки
– 2,737 тыс. руб. \шт.
определим оптимальный
уровень цены с учетом достижения максимального
значения прибыли (валовой маржи):
1) Разработаем
экономико-математическую модель задачи (прибыли):
П = Д – ТС = QЦ -VCQ – FC = Мв – FC
→ мах, (15)
где Мв – валовая маржа (разность между доходами и суммарными переменными
издержками)
Подставляем в формулу (15) соответствующие значения и
получаем:
П = Ц (251,5 – 68 Ц) – 2,737 (251,5 – 68 Ц) –
3059,2 = 251,5 Ц – 68 Ц 2 – 688,36 +186,12 Ц – 3059,2 = - 68 Ц 2 + 437,62 Ц
- 688,36 – 3059,2 (16)
Для расчета оптимальной цены возьмем производную формулы
(16) и приравняем к нулю:
d
П / d Ц = -136 Ц + 437,62 = 0
Тогда оптимальная цена равна:
Цопт = 3,22 (тыс. руб.)
Для проверки результата
проведем дополнительные расчеты в таблице 7. Для упрощения расчетов в формуле
(16) не учитываем значение FC = 3059,2 ,которое не влияет
на конечный результат.
Таблица 7
Проверка результата расчета
оптимальной цены
|
Цена
|
437,62 Ц
|
Ц2
|
136 Ц2
|
437,62 Ц –
136 Ц2
|
Валовая маржа, тыс. руб.
|
|
3,0
|
1312,9
|
9,0
|
612,0
|
700,9
|
12,5
|
|
3,05
|
1334,7
|
9,3
|
632,6
|
702,2
|
13,8
|
|
3,1
|
1356,6
|
9,6
|
653,5
|
703,1
|
14,8
|
|
3,15
|
1378,5
|
9,9
|
674,7
|
703,8
|
15,4
|
|
3,2
|
1400,4
|
10,2
|
696,3
|
704,1
|
15,7
|
|
3,25
|
1422,3
|
10,6
|
718,3
|
704,0
|
15,7
|
|
3,3
|
1444,1
|
10,9
|
740,5
|
703,6
|
15,3
|
|
3,35
|
1466,0
|
11,2
|
763,1
|
702,9
|
14,5
|
|
3,4
|
1487,9
|
11,6
|
786,1
|
701,8
|
13,5
|
|
3,45
|
1509,8
|
11,9
|
809,4
|
700,4
|
12,1
|
|
3,5
|
1531,7
|
12,3
|
833,0
|
698,7
|
10,3
|
Таким образом, из полученных расчетов видно, что оптимальная
цена с учетом округления равна 3,22 тыс. руб., при которой валовая маржа
достигает максимума.
Значение эластичности спроса позволяет перейти к методу
ценообразования на основе обеспечения прибыли.
Ставя цель получения определенной прибыли можно определить
следующее:
-
объем производства и продаж, обеспечивающий при сложившейся на рынке цене
заданный объем прибыли;
-
уровень цены продажи, обеспечивающий при определенном объеме производства
и продажи заданный уровень прибыли.
1) Предположим, что необходимо
определить количество товара, который нужно продать, чтобы получить целевую
прибыль равную 100 тыс. рублей в день.
Используя
формулу (15) определим:
П = Q Ц – FC
– VC’ * Q = 50
Тогда, Q
= (50+3059,2) : (Ц – VC’) = 3109,2 : (Ц - 2,737)
Расчеты объемов производства приведены в таблице 8.
Таблица 8
Расчеты для определения
минимального объема продаж
|
Цена единицы товара, тыс. руб.
|
Ц –2,737
|
Среднесуточная продажа товара
|
|
3,0
|
0,263
|
11822
|
|
3,1
|
0,363
|
8565
|
|
3,2
|
0,463
|
6715
|
|
3.3
|
0,563
|
5523
|
|
3,4
|
0,663
|
4690
|
|
3,5
|
0,763
|
4075
|
Таким образом, для получения прибыли в день 50 тыс. рублей
при продаже по цене 3,2 тыс.
руб. необходимо продать 6715 шт.
2) Предположим необходимо
определить уровень средней цены, чтобы получить целевую прибыль 50 тыс. рублей
в день при уровне производства и
реализации равном 3000 и более штук..
Используя
формулу (15) определяем:
Q Ц – FC – VC’ * Q = 50
Ц =
(50 + 3059,2 + 2,737Q): Q = (3109, 2+2,737 Q) : Q
Расчеты среднего уровня цены
приведены в таблице 9.
Таблица 9
Расчеты для определения
среднего уровня цены
|
Среднесуточная продажа (Q)
|
VC 'Q
|
Уровень цены (Ц)
|
VC' * Q +П + FC
|
|
3000
|
8211,0
|
3,8
|
11320,2
|
|
3500
|
9579,5
|
3,6
|
12688,7
|
|
4000
|
10948,0
|
3,5
|
14057,2
|
|
4500
|
12316,5
|
3,4
|
15425,7
|
|
5000
|
13685,0
|
3,4
|
16794,2
|
|
5500
|
15053,5
|
3,3
|
18162,7
|
Как видно из таблицы 9, с
увеличением среднесуточной продажи цена
падает.
Список
литературы
1) Базелер у., Сабов З.,
Хайнрих Й., Кох В. Основы экономической теории: принципы, проблемы, политика.
Германский опыт и российский путь. – Спб.: Питер, 2000. – 800 с.: ил.
2) Маркетинг: Учебник, практикум
и учебно- методический комплекс по маркетингу. – М.: Юрист, 2000. – 568 с.
3) Маркетинг: Энциклопедия /
Под ред. М. Бейкера. – СПб.: Питер, 2002. – 1200с.
4) Основы предпринимательской
деятельности: Финансовый менеджмент : учеб. пособ. / Под ред. В.М. Власовой. –
М.: Финансы и статистика, 2002 .- 128 с.: ил.
5) Предпринимательство: Учебник
/ Под ред. М.Г. Лапусты. – М.: Инфра – М, 2002. – 448 с.