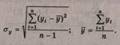
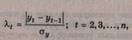2. Выявление и устранение аномальных наблюдений во временных рядах. Под аномальным уровнем понимается отдельное значение уровня временного ряда, которое не отвечает потенциальным возможностям исследуемой экономической системы и которое, оставаясь в качестве уровня ряда, оказывает существенное влияние на значения основных характеристик временного ряда, в том числе на соответствующую трендовую модель. Причинами аномальных наблюдений могут быть ошибки технического порядка, или ошибки первого рода: ошибки при агрегировании и дезагрегировании показателей, при передаче информации и другие технические причины. Ошибки первого рода подлежат выявлению и устранению. Кроме того, аномальные уровни во временных рядах могут возникать из-за воздействия факторов, имеющих объективный характер, но проявляющихся эпизодически, очень редко – ошибки второго рода; они устранению не подлежат. Для выявления аномальных уровней временных рядов используются методы, рассчитанные для статистических Совокупностей - Метод Ирвина, например, предполагает использование следующей формулы:





Где среднеквадратичное отклонение 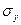рассчитывается в свою очередь с использованием формул:






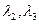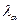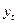Расчетные значения  и т. д. сравниваются с табличными значениями критерия Ирвина ‚и если оказываются больше табличных, то соответствующее значение  уровня ряда считается аномальным. После Выявления аномальных уровней ряда обязательно определение причин их возникновения. Если точно установлено, что они вызваны ошибками первого рода, то они устраняются либо заменой аномальных уровней простой средней арифметической двух соседних уровней ряда, либо заменой аномальных уровней соответствующими значениями по кривой, аппроксимирующей данный временной ряд.  

28.        Предварительный анализ временных рядов. Проверка наличия тренда. для определения наличия тренда в исходном временном ряду применяется несколько методов; рассмотрим два из них. Метод проверки разностей средних уровней. Реализация этого метода состоит из четырех этапов. На первом этапе исходный временной ряд разбивается на две примерно равные по числу уровней части: в первой части n1 первых уровней исходного ряда, во второй n2 остальных уровней (n1+ n2=n).

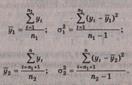На втором этапе для каждой из этих частей вычисляются средние значения и дисперсии










Третий этап заключается в проверке равенства (однородности) дисперсий обеих частей ряда с помощью F- критерия Фишера, которая основана на сравнении расчетного значения этого критерия:






с табличным (критическим) значением критерия Фишера 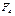с заданным уровнем значимости (уровнем ошибки) α. На четвертом этапе проверяется гипотеза об отсутствии тренда с использованием t-критерия Стьюдента. Для этого определяется расчетное значение критерия Стьюдента по формуле:

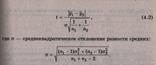Метод Фостера—Стъюарта. Этот метод обладает большими возможностями и дает более надежные результаты по сравнению с предыдущим. Кроме тренда самого ряда, он позволяет установить наличие тренда временного ряда: если тренда дисперсии нет, то рос уровней ряда постоянен; если дисперсия увеличивается, то ряд «раскачивается» и т. д. Реализация метода также содержит четыре этапа. На первом этапе производится сравнение каждого исходного временного ряда, начиная со второго уровня, со всеми предыдущими, при этом определяются две числовые последовательности

На втором этапе вычисляются величины s и d:








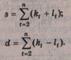
Третий этап заключается в проверке гипотез: можно ли считать случайными 1) отклонение величины s от величины μ  математического ожидания величины s для ряда, в котором уровни расположены случайным образом, 2) отклонение величины d от нуля. Эта проверка проводится с использованием расчетных значений (t-критерия Стьюдента для средней и для дисперсии:

 







где μ  — математическое ожидание величины s, определенной для ряда, в котором уровни расположены случайным образом; σ1 — среднеквадратическое отклонение для величины s; σ2 — среднеквадратическое отклонение для величины d для удобства имеются табулированные значения величин μ, σ1, σ2.

На четвертом этапе расчетные значения сравниваются ts и td с табличным значением t - критерия Стьюдента с заданным уровнем значимости tα. Если расчетное значение меньше табличного, то гипотеза об отсутствии соответствующего тренда принимается; в противном случае тренд есть.

29.        Предварительный анализ временных рядов. Сглаживание временных рядов.

С целью более четко выявить тенденцию развития исследуемого, в том числе для дальнейшего применения методов прогнозирования на основе трендовых моделей, производят сглаживание (выравнивание) временных рядов. Методы сглаживания временных рядов делятся на две группы: 1) аналитическое выравнивание с использованием кривой, проведенной между конкретными уровнями ряда так, чтобы она отображала тенденцию, присущую ряду, и одновременно освобождала его от незначительных колебаний; 2) механическое выравнивание отдельных уровней временного ряда с использованием фактических значений соседних уровней. Суть методов механического сглаживания заключается в следующем. Берется несколько

первых уровней временного ряда, образующих интервал сглаживания. Для них подбирается полином, степень которого должна быть меньше числа уровней, входящих в интервал сглаживания; с помощью полинома определяются новые, выравненные значения уровней в середине интервала сглаживания. Далее интервал сглаживания сдвигается на одна уровень ряда вправо, вычисляется следующее сглаженное значение и т. д. Самым простым методом механического сглаживания является метод простой скользящей средней. Сначала для временного ряда


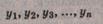
  определяется интервал сглаживания m (m < n). Если необходимо сгладить мелкие беспорядочные колебания, то интервал сглаживания берут по возможности большим; интервал сглаживания уменьшают, если нужно сохранить более мелкие колебания. При прочих равных условиях интервал сглаживания рекомендуется брать нечетным.

Метод взвешенной скользящей средней отличается от следующего метода сглаживания тем, что уровни, входящие в интервал сглаживания, суммируются с разными весами. Это связано с тем, что аппроксимация ряда в пределах интервала сглаживания осуществляется с использованием полинома не первой степени, как в предыдущем случае, а степени, начиная со второй.

К этой же группе методов выравнивания временных рядов примыкает метод экспоненциального сглаживания - Его особенность заключается в том, что в процедуре нахождения уровня используются значения только предшествующих уровней ряда, взятые с определенным весом, причем все наблюдения уменьшается по мере удаления его от времени, для которого определяется сглаженное значение уровня ряда.













































31.        Прогнозирование экономических показателей с помощью модели Брауна.

−         Модель Брауна может отображать развитие не только в виде линейной тенденции, но также в виде случайного процесса, не имеющего тенденции, а также в виде изменяющейся параболической тенденции. Соответственно различают модели Брауна:  

−         Нулевого порядка, которая описывает процессы, не имеющие тенденции развития.

−         Первого порядка (Y(t+k)=A0+A1*k). Коэффициент А0 – значение, близкое к последнему уровню, и представляет как бы закономерную составляющую этого уровня.

Второго порядка, отражающей развитие в виде параболической тенденции с изменяющимися «скоростью» и «ускорением». Порядок модели обычно определяют либо априорно на основе визуального анализа графика процесса (есть ли тренд и близок ли он к линейной функция), знаний законов развития характера изменения исследуемого явления, либо методом проб, сравнивая статистические характеристики моделей различного порядка на участке ретроспективного прогнозирования. Рассмотрим этапы построения линейной адаптивной модели Брауна. Этап 1. По первым пяти точкам временного ряда оцениваются начальные значения Ао и А1 параметров модели с помощью метода наименьших квадратов для линейной аппроксимации:

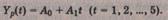Этап 2. С использованием параметров Ао и А1 по модели Брауна находим прогноз на один шаг (К = 1):



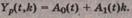
Этап 3. Расчетное значение Yp(t,k) экономического показателя сравнивают с фактическим Y(t) и вычисляется величина их расхождения (ошибки).

Этап 4. В соответствии с этой величиной корректируются параметры модели.

Этап 5. По модели со скорректированными параметрами А0 и А1 находят прогноз на следующий момент времени. Этап 6. Интервальный прогноз строится как для линейной модели кривой роста.

В моделях Брауна и Хольта параметры сглаживания характеризуют степень адаптации модели к изменению ряда наблюдений Они определяют скорость реакции модели на изменения, происходящие в развитии: Чем они больше, тем быстрее реагирует модель на изменения. Обычно для устойчивых рядов их величина большая, а для неустойчивых — маленькая. В различных методах прогнозирования используется различный подход к их определению. Их можно взять фиксированными, а наилучшее значение определить методом подбора, чтобы ошибка прогноза на один шаг вперед была наименьшей. При использовании компьютера это не представляет труда.



















































39. Экспоненциальные и S-образные кривые роста.

Использования экспоненциальных кривых роста предполагает, что дальнейшее развитие зависит от достигнутого уровня, например, прирост зависит от значения функции. В экономике чаще всего применяются две разновидности экспоненциальных (показательных) кривых: простая экспонента и модифицированная экспонента. Простая экспонента представляется в виде функции 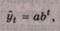где a и b — положительные числа, при этом если b больше единицы, то функция возрастает с ростом времени t, если b меньше единицы — функция убывает. Модифицированная экспонента имеет вид

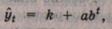
где постоянные величины: а меньше нуля, b положительна и меньше единицы, а константа k носит название асимптоты этой функции, т.е. значения функции неограниченно приближаются (снизу) к величине k . В экономике достаточно распространены процессы, которые сначала растут медленно, затем ускоряются, а затем снова замедляют свой рост, стремясь к какому-либо пределу. В качестве примера можно привести процесс ввода некоторого объекта в промышленную эксплуатацию, процесс изменения спроса на товары, обладающие способностью достигать некоторого уровня насыщения, и др. Для моделирования таких процессов используются так называемые S-образные кривые роста, среди которых выделяют кривую Гомперца и логистическую кривую. Кривая Гомперца имеет аналитическое выражение

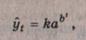
где а, b — положительные параметры, причем b  меньше единицы; параметр k -асимптота функции. В кривой Гомперца выделяются четыре участка: на первом — прирост функции незначителен, на втором — прирост увеличивается, на третьем участке прирост примерно постоянен, на четвертом — происходит замедление темпов прироста и функция неограниченно приближается к значению k. В результате конфигурация кривой напоминает латинскую букву S. На основании кривой Гомперца описывается, например динамика показателей уровня жизни; модификации этой кривой используются в демографии для моделирования показателей смертности и т.д. Логистическая кривая, или кривая Перла—Рида — возрастающая функция, наиболее часто выражаемая в виде

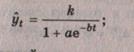
 Другие виды этой кривой:

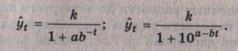
Конфигурация графика логистической кривой близка графику кривой Гомперца, но в отличие от последней логистическая кривая имеет точку симметрии, совпадающую с точкой перегиба.



































38.        Основные этапы реализации симплексного метода.

1.         Симплекс-метод с естественным базисом, алгоритм метода.  

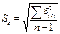Для его применения КЗЛП должна содержать единичную подматрицу M*N. В этом случае очевиден начальный опорный план (неотрицательное базисное решение системы ограничений КЗЛП). Проверка на оптимальность опорного плана происходит с помощью признака оптимальности. Переход к другому опорному плану проводится с помощью преобразований Жордана-Гаусса. Полученный новый опорный план проверяется снова на оптимальность и т.д. Процесс заканчивается за конечное число шагов, причем на последнем шаге либо выявляется неразрешимость задачи, либо получается оптимальный опорный план и соответствующее ему оптимальное значение ЦФ. Признак оптимальности состоит из двух теорем: 1.Если для всех векторов А1,А2,…,Аn системы ограничений выполняется условие ∆j = Zj – Cj ≥ 0, где Zj = ∑ Ci Aij, то полученный опорный план является оптимальным.   2.Если для некоторого вектора, не входящего в базис, выполняется условие ∆j = Zj – Cj < 0, то можно получить новый опорный план, для которого значение ЦФ будет больше исходного, при этом могут быть два случая  а)Если все компоненты вектора, подлежащего вводу в базис, не положительны , то ЗЛП не имеет решения.  б)Если имеется хотя бы одна положительная компонента у вектора, подлежащего вводу в базис, то можно получить новый опорный план.

На основании признака оптимальности в базис вводится вектор Ak , давший минимальную отрицательную величину симплекс-разности: ∆k = min (Zj – Cj), j = 1,‾n.

Чтобы выполнялось условие не отрицательности значений опорного плана, выводится из базиса вектор Ar, который  дает минимальное положительное оценочное отношение:  Q = min Bi / Aik = Br/Ark, Aik >0, i = 1,m. Строка Arназывается направляющей, столбец Ak и элемент Ark направляющими.

Элементы направляющей строки в новой симплекс-таблице вычисляются по формулам:  a’rj = arj / ark, j = 1,n. 

Элементы  i-той строки:  a’ij = (aij ark – arj aik) / ark, i = 1,m, j = 1,n, i ≠ r.

Значения нового опорного плана: b’r = br / ark для i=r; b’i = (bi ark – br aik) / ark для i≠r.   

Процесс решения продолжают либо до получения нового оптимального плана либо до установления неограниченности ЦФ. Если среди оценок оптимального плана нулевые только оценки, соответствующие базисным векторам, то это говорит об единственности оптимального плана. Если же нулевая оценка соответствует вектору, не входящему в базис, то это значит, что оптимальный план не единственный.

2.         Построение М-задачи .  

Симплекс-метод с искусственным базисом применяется в тех случаях, когда затруднительно найти первоначальный план опорный план КЗЛП. Этот метод заключается в применении правил симплекс-метода к М-задаче. Она получается из исходной добавлением к левой части векторного уравнения таких искусственных единичных векторов с соответствующими неотрицательными искусственными переменными, чтобы вновь полученная матрица содержала систему единичных, линейно-независимых векторов. В линейную форму исходной задачи добавляется в случае ее максимизации слагаемое, представляющее собой произведение числа (-М) на сумму искусственных переменных, где М –достаточно большое число. В полученной задаче первоначальный опорный план очевиден. При применении к этой задаче симплекс-метода оценки ∆j теперь будет зависеть от буквы М. Для сравнения оценок нужно помнить, что М- достаточно большое число. В процессе решения М-задачи следует вычеркивать в симплекс-таблице искусственные векторы по мере их выхода из базиса. Если все искусственные векторы вышли из базиса, то получаем исходную задачу. Если в оптимальном решении М-задачи хотя бы одна из искусственных переменных отлична от нуля, то система ограничений исходной задачи несовместна (задача неразрешима). В случае неразрешимости М-задачи будет неразрешима и исходная задача.



























25. Построение точечных и интервальных прогнозов при использовании моделей кривых роста.

Точечный прогноз — это прогноз, которым называется единственное значение прогнозируемого показателя. Это значение определяется подстановкой в уравнение выбранной кривой роста величины времени , соответствующей периоду упреждения: t=n+1; t=n+2 и т. д. Такой прогноз называется точечным, так как на графике его можно изобразить в виде точки. Очевидно, что точное совпадение фактических данных в будущем и прогностических точечных оценок маловероятно. Поэтому точечный прогноз должен сопровождаться двусторонними границами, та указанием интервала значений, в котором с достаточной долей уверенности можно ожидать появления прогнозируемой величины. Установление такого интервала называется интервальным прогнозом. Интервальный прогноз на базе трендовых моделей осуществляется путем расчета доверительного интервала — такого интервала, в котором с определенной вероятностью можно ожидать появления фактического значения прогнозируемого экономического показателя. Расчет доверительных интервалов при прогнозировании с использованием кривых роста опирается на выводы и формулы теории регрессий. Перенесение выводов теории регрессий на временные экономические ряды не совсем правомерно, так как динамические ряды, как выше уже отмечали, отличаются от статистических совокупностей. Поэтому к оцениванию доверительных интервалов для кривых роста следует подходить с известной долей осторожности. Методы, разработанные для статистических совокупностей, позволяют определить доверительный интервал, зависящий от стандартной ошибки оценки прогнозируемого показателя, от времени упреждения прогноза, от количества уровней во временном ряду и от уровня значимости (ошибки) прогноза. Стандартная (средняя квадратическая) ошибка оценки прогнозируемого показателя Sŷ определяется по формуле:





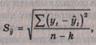
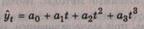
где у — фактическое значение уровня временного ряда для времени t; ŷ— расчетная оценка соответствующего показателя по модели (например, по уравнению кривой роста); n — количество уровней в исходном ряду; k— число параметров модели. 26.Правило построения двойственной задачи, математическая запись.

1. Если исходная задача сформулирована на max, то двойственная д.б. сформулирована на минимум, и наоборот.

2. Матрица А, составленная из коэффициентов неизвестных в системе ограничений двойственной задачи является транспонированной матрице А исходной задачи.

3. Число переменных в двойственной задаче равно числу функциональных переменных исходной задачи, а число ограничений этой задачи равно числу переменных в исходной задаче.

4. Коэффициенты неизвестных в целевой функции двойственной задачи являются свободными членами в системе ограничений исходной задачи. А правыми частями в ограничениях двойственной задачи – коэффициенты при неихвестных в целевой функции исходной задачи.

5. Если в исходной задаче, сформулированной на максимум, все функциональные ограничения будут иметь знак < или =, то в двойственной задаче все неизвестные неотрицательны. Если в исходной задаче, сформулированной на максимум, присутствуют уравнения или ограничений тип > или =, то соответствующие двойственные оценки будут отрицательными. 

Математическая запись:

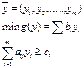
Теоремы двойственности и их использование для анализа оптимальных решений.

Теорема 1 (основная теорема двойственности)

1 часть: Если одна из двойственных задач разрешима, то разрешима и другая. Причем экстремальное значение ЦФ задач равны  max f(x)=f(x*)=min Ψ(y)= Ψ (y*).    2 часть: Если одна из двойственных задач неразрешима, то неразрешима и другая.

Теорема 2 (о дополняющей не жесткости): Если при подстановке компонент оптимального плана в систему ограничений исходной задачи i-тое ограничение обращается в неравенство, то i-тая компонента оптимального плана двойственной задачи равна 0. Если i-тая компонента оптимального плана двойственной задачи  положительна, то i-тое ограничение  исходной задачи удовлетворяется ее оптимальным решением как строгое неравенство.  Xi* (∑AijYi*- Ci) = 0       Yi* (∑AijXj*- Bi) = 0



24.        Построение моделей. Оценка параметров кривых роста с помощью метода наименьших квадратов (МНК).

Рассмотрим методы определения параметров отобранных кривых роста. Параметры полиномиальных кривых оцениваются, как правило, методом наименьших квадратов, суть которого заключается в том, чтобы сумма квадратов отклонений фактических уровней ряда от соответствующих выравненных по кривой роста значений была наименьшей. Этот метод приводит к системе так называемых нормальных уравнений для определения неизвестных параметров отобранных кривых.

Для полинома первой степени:




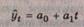
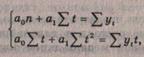система нормальных уравнений имеет вид:









где знак суммирования распространения на все моменты наблюдения исходного временного ряда.

Аналогичная система для полинома второй степени




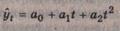
Имеет вид

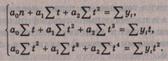
Для полинома третей степени





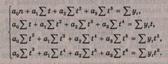Система нормальных уравнений записывается следующим образом:


Параметры экспоненциальных и S-образных кривых находятся более сложными методами. Для простой экспоненты




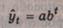
Предварительно логарифмируют выражение по некоторому основанию:





т.е. для логарифма функции получают линейное выражение, а затем для неизвестных параметров log a и log b составляют на основе метода наименьших квадратов систему нормальных уравнений, аналогичную системе для полинома первой степени. Решая эту систему, находят логарифмы параметров, а затем и сами параметры модели.





































23.        Построение моделей. Адаптивные модели прогнозирования.

Адаптивные модели прогнозирования — это модели дисконтирования данных, способные быстро приспосабливать свою структуру и параметры к изменению условий. Инструментом прогноза в адаптивных моделях, как и в кривых роста, является математическая модель с единственным фактором «время». При оценке параметров адаптивных моделей в отличие от рассматриваемых ранее моделей «кривых роста» а наблюдениям (уровням ряда) присваиваются различные веса в зависимости от того, насколько сильным признается их влияние на текущий уровень. Это позволяет учитывать изменения в тенденции, а также любые колебания, в которых прослеживается закономерность. Все адаптивные модели базируются на двух схемах: скользящего среднего (СС—модели) и авторегрессии (АР—модели). Согласно схеме скользящего среднего, оценкой текущего уровня является взвешенное среднее всех предшествующих уровней, причем веса при наблюдениях убывают по мере удаления от последнего уровня, т. е. информационная ценность наблюдений признается тем большей, чем ближе они к концу интервала наблюдений. Такие модели хорошо отражают изменения, происходящие в тенденции, но в чистом виде не позволяют отражать колебания.

Общая схема построения адаптивных моделей может быть представлена следующим образом. По нескольким первым уровням ряда оцениваются значения параметров модели. По имеющейся модели строится прогноз на один шаг вперед, причем его отклонение от фактических уровней ряда расценивается как ошибка прогнозирования, которая учитывается в соответствии с принятой схемой корректировки модели. Далее по модели со скорректированными параметрами рассчитывается прогнозная оценка на следующий момент времени и т.д. Таким образом, модель постоянно «впитывает» новую информацию и к концу периода обучения отражает тенденцию развития процесса, существующую в данный момент. В практике статистического прогнозирования наиболее часто используются две базовые СС-модели — Бранла и Хольта, первая из них является частным случаем второй. Эти модели представляют процесс развития как линейную тенденцию с постоянно изменяющимися параметрами.

22.Постановка и экономико-математическая модель открытой транспортной задачи.  

Имеется m пунктов производства однородного продукта с объемами производства  A1,A2,…,Am. Имеется n пунктов потребления этого продукта с объемами потребления b1,b2,…,bn. Известны оценки С= (Cij) M*N  транспортных затрат на перевозку единицы груза от i-того поставщика к j-тому потребителю (по коммуникации от i к j). Надо так прикрепить потребителей к поставщикам, чтобы минимизировать суммарные транспортные затраты на перевозку груза.  ЭММ ТЗ:  Обозначим через Xij, i=1,m  j=1,n объемы перевозок по коммуникации  i→j, т.е. в рассмотрение вводится матрица X=(Xij)m*n.


Min ∑ ∑ Cij Xij

∑ Xij = Ai,  i=1,m

∑ Xij = Bj,  j=1,n

 

Если не выполняются условия баланса между спросом и предложением  ∑Ai = ∑Bj, то ТЗ называется открытой, при этом могут быть 2 случая. 1 случай: ∑Ai > ∑Bj, тогда ограничения имеют вид ∑ Xij ≤  Ai,  i=1,m. 2 случай: ∑Ai < ∑Bj. Тогда ограничения имеют вид ∑ Xij ≤ Bj,  j=1,n

34.Структура временных рядов экономических показателей.  

Временной ряд экономических показателей можно разложить на 4 структуро-образующих элемента:

1. Тренд (Ut) – устойчивое систематическое изменение процесса в течение продолжительного времени.

2. Сезонная компонента (Vt) – колебания, носящие строго периодический или близкий к нему характер и завершающиеся в течении года.

3. Циклическая компонента (Ct) – период колебаний составляет несколько лет.

4. Случайная компонента (εt) – составная часть временного ряда, остающаяся после выделения из него регулярных компонент.

























14.Основные понятия теории игр, игры с природой.

Математической теорией конфликтных ситуаций является теория игр. В игре могут сталкиваться интересы двух или нескольких противников; существуют игры с бесконечным множеством игроков. Если во множественной игре игроки образуют коалиции, то игра называется коалиционной; если таких коалиций две, то игра сводится к парной.

На промышленных предприятиях теория игр может применяться для выбора оптимальных решений, например, при создании рациональных запасов сырья, материалов, полуфабрикатов, когда противоборствуют две тенденции: увеличения запасов, гарантирующих бесперебойную работу производства, и сокращения запасов в целях минимизации затрат на их хранение. В сельском хозяйстве теория игр может применяться при решении таких экономических задач, как выбор для посева одной из возможных культур, урожай которых зависит от погоды, если известны цена единицы той или иной культуры и средняя урожайность каждой культуры в зависимости от погоды (например, будет ли лето засушливым, нормальным или дождливым); в этом случае одним из игроков выступает сельскохозяйственное предприятие, стремящееся обеспечить наибольший доход, а другим — природа. Решение подобных задач требует полной определенности в формулировании их условий (правил игры); установления количества игроков, выявления возможных стратегий игроков, возможных выигрышей. Важным элементом в условии игровых задач является стратегия, т.е. совокупность правил, которые в зависимости от ситуации в игре определяют однозначный выбор действий данного игрока. Если в процессе игры игрок применяет попеременно несколько стратегий, то такая стратегия называется смешанной, а ее элементы — чистыми стратегиями. Количество стратегий у каждого игрока может быть конечным и бесконечным, в зависимости этого игры подразделяются на конечные и бесконечные. Важными являются понятия оптимальной стратегии, цены игры, среднего выигрыша. Эти понятия находят отражение в определении решения игры.

Одним из основных видов игр являются матричные игры, которыми называются парные игры с нулевой суммой (один игрок выигрывает столько, сколько проигрывает другой) при условии, что каждый игрок имеет конечное число стратегий.

Во многих игровых задачах в сфере экономики неопределенность вызвана не сознательным противодействием противника, а недостаточной осведомленностью об условиях, в которых действуют стороны.

Подобного рода игры называются играми с природой. В этих случаях строки матрицы игры соответствуют стратегии игрока, а столбцы — состояниям «природы». В ряде случаев при решении такой игры рассматривают матрицу рисков. При решении игр с природой используется также ряд критериев: критерий Сэвиджа, критерий Вальда, Критерий Гурвица и др. При максиминном критерии Вальда оптимальной считается та стратегия лица, принимающего решение (ЛПР), которая обеспечивает максимум минимального выигрыша; применяя этот критерий, ЛПР в большей степени ориентируется на наихудшие условия. Критерий минимаксного риска Сэвиджа предполагает, что оптимальной является та стратегия, при которой величина риска в наихудшем случае минимальна. При использовании критерия «пессимизм — оптимизм» Гурвица ЛПР выбирает некоторый так называемый «коэффициент пессимизма» q.

13.        Основные понятия о системах массового обслуживания, примеры их применения.

Методами теории массового обслуживания могут быть решены многие задачи исследования процессов, происходящих в экономике. Так, в организации торговли эти методы позволяют определить оптимальное количество торговых точек данного профиля, численность продавцов, частоту завоза товаров и другие параметры. Другим характерным примером систем массового обслуживания могут служить склады или базы снабженческо-сбытовых организаций, и задача теории массового обслуживания в данном случае сводится к тому, чтобы установить оптимальное соотношение между числом поступающих на базу требований на обслуживание и числом обслуживающих устройств, при котором суммарные расходы на обслуживание и убытки от простоя транспорта были бы минимальными. Теория массового обслуживания может найти применение и при расчете площади складских помещений, при этом складская площадь рассматривается как обслуживающее устройство, а прибытие транспортных средств под выгрузку — как требование. Модели теории массового обслуживания применяются также при решении ряда задач организации и нормирования труда, других социально-экономических проблем. Системы массового обслуживания могут быть классифицированы по ряду признаков. 1.В зависимости от условий ожидания начала обслуживания различают: • СМО с потерями (отказами), • СМО с ожиданием.

В СМО с отказами требования, поступающие в момент, когда все каналы обслуживания заняты, получают отказ и теряются. Классическим примером системы с отказами является телефонная станция. Если вызываемый абонент занят, то требование на соединение с ним получает отказ и теряется. В СМО с ожиданием требовакие, застав все обслуживающие каналы занятыми, становятся в очередь и ожидает, пока не освободится один из обслуживающих каналов. СМО, допускающие очередь, но с ограниченным числом требований в ней, называются системами с ограниченной длиной очереди. СМО, допускающие очередь, но с ограниченным сроком пребывания каждого требования в ней, называются системами с ограниченным временем ожидания. 2. По числу каналов обслуживания СМО делятся на • одноканальные; • многоканальные. 3. По месту нахождения источника требований СМО делятся на: • разомкнутые, когда источник требования находится вне системы; • замкнутые, когда источник находится в самой системе. Примером разомкнутой системы может служить ателье по ремонту телевизоров. Здесь неисправные телевизоры — это источник требований на их обслуживание, находятся вне самой системы, число требований можно считать неограниченным. ТС замкнутым СМО относится, например, станочный участок в котором станки являются источником неисправностей, а следовательно, источником требований на их обслуживание, например, бригадой наладчиков. Методы и модели, применяющиеся в теории массового обслуживания, можно условно разделять на аналитические и имитационные. Аналитические методы теории массового обслуживания позволяют получить характеристики системы как некоторые функции параметров ее функционирования. Благодаря этому появляется возможность проводить качественный анализ влияния отдельных факторов на эффективность работы СМО. Имитационные методы основаны на моделировании процессов массового обслуживания на ЭВМ и применяются, если невозможно применение аналитических моделей.

 Важная характеристика СМО — время обслуживания требований в системе. Время обслуживания одного требования является, как правило, случайной величиной и, следовательно, может быть описано законом распределения. Наибольшее распространение в теории и особенно в практических приложениях получил экспоненциальный закон распределения времени обслуживания.

СМО с ожиданием можно разбить на две большие группы: замкнутые и разомкнутые. К замкнутым относятся системы, в которых поступающий поток требований возникает в самой системе и ограничен. Например, мастер, задачей которого является наладка станков в цехе, должен периодически их обслуживать. Каждый налаженный станок становится потенциальным источником требований на наладку.

Если питающий источник обладает бесконечным числом требований, то системы называются разомкнутыми. Примерами подобных систем могут служить магазины, кассы вокзалов, портов и др.











11. Назначение и область применения сетевых моделей. Основные элементы сетевой модели.

Сетевой моделью называется экономико-математическая модель, отражающая комплекс работ (операций) и событий, связанных с реализацией некоторого проекта, в их логической и технологической последовательности и связи. Анализ сетевой модели, представленной в графической или табличной форме, позволяет, во-первых, более четко выявить взаимосвязи этапов реализации проекта и, во-вторых, определить наиболее оптимальный порядок выполнения этих этапов в целях, например, сокращения сроков выполнения всего комплекса работ. Таким образом, методы сетевого моделирования относятся к методам принятия оптимальных решений. Основные понятия СМ: событие, работа и путь. Работа характеризует материальное действие, требующее использования ресурсов, или логическое, требующее лишь взаимосвязи событий. При графическом представлении работа изображается стрелкой, которая соединяет два события. Она обозначается парой заключенных в скобки чисел (i,j), где i — номер события, из которого работа выходит, а j — номер события, в которое она входят. Работа не может начаться раньше, чем свершится событие, из которого она выходит.

Событиями называются результаты выполнения одной или нескольких работ. Они не имеют протяженности во времени. Событие свершается в тот момент, когда оканчивается последняя из работ, входящая в него. События обозначаются одним числом и при графическом представлении СМ изображаются кружком, внутри которого проставляется его порядковый номер (i = 1, 2, ..., N). В СМ имеется начальное событие (c номером 1), из которого работы только выходят, и конечное событие (с номером N), в которое работы только входят. Путь — это цепочка следующих друг за другом работ, соединяющих начальную и конечную вершины.

20.Оценка точности модели кривой роста, выбор наилучшей кривой роста.  

Для адекватных моделей имеет смысл ставить задачу оценки точности. Точность модели характеризуется величиной отклонения выхода модели от реального значения моделируемой переменной.

В качестве статистических показателей точности применяются: среднее квадратическое отклонение, средняя относительная ошибка аппроксимации, коэффициент сходимости, коэффициент детермизации. n-количество уровней ряда, k-число определяемых параметров модели, yt-оценка уровней ряда по модели, yср – среднее арифмитическое значение уровней ряда.

1.Временной ряд, тренд, трендовая модель. Получение трендовой модели средствами Excel.

Временной ряд – это набор чисел, привязанный к последовательным, обычно равноотстоящим моментам времени. Числа, составляющие временной ряд и получающиеся в результате наблюдения за ходом некоторого процесса, называются уровнями временного ряда, или элементами. Интервал между двумя последовательными моментами времени называют тактом (шагом, квантом). Длина временного ряда – количество входящих в него уровней n. Временной ряд обозначают y(t), или yt, где t=1,2,…,n. Структурные компоненты временного ряда: Детерминирующая составляющая (тренд, сезонный эффект, циклическая компонента) и случайная составляющая («белый шум», авторегрессия, скользящее среднее, смешанная).

Тренд, или тенденция f(t) представляет собой устойчивую закономерность, наблюдаемую в течении длительного периода времени. Обычно тренд описывается с помощью той или иной неслучайной функции Fтр(t) (аргументом которой является время), как правило монотонной. Эту функцию называют функцией тренда, или просто трендом.

Под трендом понимается изменение, определяющее общее направление развития, основную тенденцию временных рядов. Экономико-математическая динамическая модель, в которой развитие моделируемой экономической системы отражается через тренд ее основных показателей, называется трендовой моделью. Прогнозирование экономических процессов, представленных одномерными временными рядами, сводится к выполнению следующих основных этапов: 1. Предварительный анализ данных. 2. Построение моделей: формирование набора аппроксимирующих функций (кривых роста) и численное оценивание параметров моделей. 3. Проверка адекватности моделей и оценка их точности. 4. Выбор лучшей модели. 5. Рассчет точечного и интервального прогнозов.

















9.Каноническая форма записи ЗЛП. Способы приведения ЗЛП к каноническому виду.

Канонической формой записи задачи линейного программирования называют задачу вида (запись с использованием знака суммирования):

найти





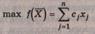
При ограничениях






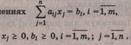
Векторная форма записи КЗЛП имеет вид:

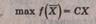Найти





При ограничениях

Где

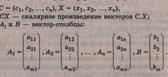
Матричная форма записи КЗЛП:



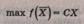
при условиях








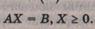
При этом запись Х>=0 понимают как вектор (или вектор-столбец в зависимости от контекста), у которого все компоненты (элементы) неотрицательны. Приведение ЗЛП к каноническому виду осуществляется введением в левую часть соответствующего ограничения вида k -й дополнительной переменной хn+k>=0 со знаком — в случае ограничения типа и знаком + в случае ограничения типа <=.

6.Задача о назначениях, постановка и ЭММ.

С ее помощью можно получить ответ на вопрос типа Как распределить рабочих по станкам, чтобы общая выработка была наибольшей? Как наилучшим образом распределить экипажи самолетов? Как назначить людей на разные должности? Исходные данные группируются в таблице, которая называется матрицей оценок, а результаты – в матрице назначений. ЕЕ постановка:  Имеется n –работников, которые могут выполнить n-работ, причем использование i-того работника на j-той работе приносит доход Cij. Требуется  поручить каждому из работников выполнение одной вполне определенной работы, чтобы максимизировать  суммарный доход. Задача в том, чтобы найти распределение X=(Xij) работников по работам, которое максимизирует ЦФ.

F(x)=∑∑Cij Xij → max

∑Xij=1, i=1,n   (1)

∑Xij=1, j=1,n  (2)

причем Xij= либо 0 либо 1  для всех i,j=1,n

Ограничение (1) отражает условие того, что за каждым работником может быть закреплена только одна работа, а ограничение (2) означает, что для выполнения каждой работы может быть выделен только один работник.   При решении таких задач используются алгоритмы и методы решения транспортных задач, в частности метод потенциалов.












8.           Имитационное моделирование, основные понятия и примеры применения.

Метод машинной имитации- метод экспериментального изучения социально-экономических систем с помощью ЭВМ. Машинная имитация применяется тогда, когда реальный экономический эксперимент по каким-либо причинам невозможен, и тогда имитация выступает в качестве замены реального эксперимента либо в качестве предварительного этапа, позволяющего принять более обоснованное решение о проведении такого эксперимента.

При машинной имитации формируется так называемая имитационная система, в которую входят имитационная модель, имитирующая исследуемый процесс, и набор алгоритмов и программ, предназначенных как для обеспечения диалога человека и ЭВМ (внутреннее математическое обеспечение), так и для решения задач типа ввода и вывода информации, формирования базы данных и т.д. (внешнее математическое обеспечение). Имитационная модель при этом сама является своего рода программой для ЭВМ. Практическое применение этой модели заключается в наблюдении за результатами весьма многовариантных расчетов по такой программе при различных задаваемых значениях вводимых экзогенных переменных. В процессе анализа этих результатов могут быть сделаны выводы о поведении системы без ее построения, если эта система только проектируется, без вмешательства в ее функционирование, если это действующая система, и без ее разрушения, если целью эксперимента является определение пределов воздействия на систему. Таким образом могут быть достигнуты цели экономико-математического моделирования в тех случаях, когда аналитическое решение невозможно. Процесс последовательной разработки имитационной модели начинается с создания простой модели, которая затем постепенно усложняется в соответствии с предъявляемыми решаемой проблемой требованиями. В каждом цикле имитационного моделирования можно выделять следующие этапы: - 1. Формулирование проблемы: описание исследуемой проблемы и определение целей исследования. 2. Разработка модели: логико—математическое описание моделируемой системы в соответствии с формулировкой проблемы. 3. Подготовка данных: идентификация, спецификация я сбор данных. 4. Трансляция модели: перевод модели со специальных имитационных языков, используемых на этапе 2, на язык, приемлемый для используемой ЭВМ. 5 Верификация: установление - правильности машинных программ.

6. Валидация: оценка требуемой точности и адекватности имитационной модели. 7. Планирование: определение условий проведения машинного эксперимента с имитационной моделью. 8. Экспериментирование: многократный прогон имитационной модели на ЭВМ для получения требуемой информации. 9. Анализ результатов: изучение результатов имитационного эксперимента для подготовки выводов и рекомендаций по решению проблемы. 10. Реализация и документирование: реализация рекомендаций, полученных на основе имитации, и составление документации по модели и ее использованию.

33.Процедура прогнозирования с использованием кривых роста, этапы и  наиболее часто используемые кривые роста.

Этапы: 1. Предварительный анализ данных. 2. Построение моделей: формирование набора аппроксимирующих функций (кривых роста) и численное оценивание параметров моделей. 3. Проверка адекватности моделей и оценка их точности. 4. Выбор лучшей модели. 5. Расчет точечного и интервального прогонозов.

Наиболее часто используемы кривые роста: полиномиальные 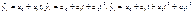, экспоненциальные 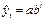, где a и b – положительные числа, S-образные

35.Требования, предъявляемые к исходной информации при моделировании экономических процессов на основе временных рядов.  

1. Сопоставимость достигается в результате одинкаовым подходом к наблюдениям на разных этапах формирования ряда динамики. Одни  и те же единицы измерения, одинаковый шаг наблюдений, один и тот же интервал времени, одна и та же методикаодни и те же элементы, относящиесяк неизменной совокупности.

2. Однородность данных – отсутствие сильных изломов тенденций, а также аномальных наблюдений.

3. Представительность данных хар-ся их полнотой. Число наблюдений должно быть достаточным для потсаленной задачи.

4. Устойчивость – преобладание закономерности над случайностью.










37.        ЭММ. Понятие, пример, общая классификация ЭММ.

В основе всех совр.фин.расчетов лежат те или иные мат.модели исследуемых эк.процессов, т.е. основным  методом является метод моделирования. Этот метод основан на принципе аналогии,  т.е. возможности изучения не самого исходного объекта, а некоторого искусственного созданного объекта – модели. Модель вообще это некоторый объект способный заменить исследуемый с целью получения нового знания. Модели подразделяются на физические и абстрактные. Физические это макеты, конструкции и т.д. Абстрактные это словесно-описательные и мат.модели. Словесно-описательные это эк.сценарии, программы, пояснительные записки. ЭММ это мат.образ, мат.описание принципиальных сторон исследуемого эк.процесса, проблемы, задачи. ЭММ средствами экономики и мат-ки отражает существо исследуемой эк.проблемы. ЭММетоды это методы разработки, исследования и принятия решений по ЭММ. ЭММ подразделяют на макро- и микроэкономические, прескриптивные и дескриптивные. К макро относят модели, реализующие народно-хозяйственные пропорции, межотраслевые и межрегиональные пропорции и эк.взаимоотношения. К микро  - модели на уровне взаимоотношений хозяйствующего субъекта, модели внутри фирменного планирования. Прескриптивные (нормативные) это модели отвечают на вопрос: Какой вариант управленческого поведения лучше? (оптимизационные модели). Дескриптивные это модели отвечают на вопрос: А что будет, если? (балансовые модели, производственные функции). Многим задачам в экономике отвечают оптимизационные (экстремальные) ЭММ.


3.   Графический метод решения задачи линейного программирования.

Если в задаче линейного программирования ограничения заданы в виде неравенств с двумя переменными, то задача может быть решена графически. Графический метод решения ЗЛП состоит из этапов: 1.Стоится многоугольная область допустимых решений ЗЛП. 2.Строится вектор-градиент целевой функции. Начало в т.О(0,0), а вершина в т.(df/dx1; df/dx2)=(C1;C2). 3.Строим линию уровня c1x1+c2x2=a, a=const. Линия уровня это прямая перпендикулярная вектору-градиенту. Передвигаемся в направлении этого вектора. В случае максимизации ЦФ до тех пор, пока не покинет ОДР. Предельная точка ОДР  при этом движении и является точкой max ЦФ. 4.Для нахождения координат указанной предельной точки, достаточно решить 2 уравнения прямых, получаемых из соответствующих ограничений и дающих в пересечении точку max. Значение ЦФ найденное в этой точке является max. При минимизации ЦФ линия уровня перемещается в  направлении противоположном вектору-градиенту.


16.Основные этапы применения математических методов в финансово-экономических расчетах (иллюстрация на конкретном примере).  

В процессе решения эк.задач с применением мат.методов можно выделить 4 осн.этапа: 1.Постановка эк.задачи, проблемы. Здесь осуществляется описание экономико-организационной задачи. 2.Мат.моделирование. Здесь разрабатывается ЭММ задачи. 3.Получение решения по модели. Здесь осуществляется реализация ЭММ. 4.Внедрение полученного решения. Разработка рекомендаций, предложений в доступном и наглядном виде для работника.      В процессе исследований и принятия решений с помощью ЭММ  приходится возвращаться заново на те или иные этапы.

12.задача линейного программирования, основные элементы и понятия.

Реализовать на практике принцип оптимальности это значит разработать и получить решение по модели: max(min) максимизировать или минимизировать функцию f(x) при ограничениях, где f(x1,x2,…,xn) – математическая запись критерия оптимальности -ЦФ.    Max(min) f(x)=f(x1,x2,…,xn),x  є D.

Обычно, приведенную модель записывают в виде:

Max(min) f(x1,x2,…,xn)

g1(x1,x2,…xn)   {≤ , = , ≥ } b1           (1)

g2(x1,x2,…xn)   {≤ , = , ≥ } b2          (2)

gn(x1,x2,…xn)   {≤ , = , ≥ } bn

xi  ≥ 0,  i=1,¯ n                                (3)


17.Особые случаи решения ЗЛП графическим методом.

#1 max (3x1+5x2) ограничения: x1+x2 ≥ 2    4x1+2x2 ≤  2 при x1,2 ≥ 0

Задача неразрешима, вследствии противоречивости ограничений

#2 max (3x1+2x2)   x1-x2  ≤ 1   2x1+x2 ≥ 1 при x1,2 ≥ 0

Задача неразрешима вследствие неограниченности ЦФ на ОДР.

#3 Случай не единственности решения max (8x1+10x2)   5x1+x2 ≤ 15   4x1+5x2  ≤ 40  при x2 ≥ 3    x1 ≥ 0

Линия уровня  8x1+10x2 =a параллельна  одной из линий по границе ОДР. Это значит, что задача имеет бесконечное множество оптимальных решений (его задают координаты точек отрезка ВС).






4.Двойственные оценки в ЗЛП, интервалы устойчивости двойственных оценок, определение средствами Excel.

С каждой задачей линейного программирования тесно связана другая линейная задача , называемая двойственной; первоначальная задача называется исходной или прямой.

Связь исходной и двойственной задачи заключается, в частности, в том, что решение одной из них может быть получено непосредственно из решения другой. Переменные двойственной задачи 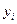  называются двойственными оценками.

Модель двойственной задачи имеет вид:

   g()=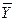       

     

     

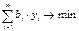
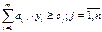
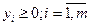
Теорема об оценках: значения переменных 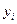  в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов  b  системы ограничений – неравенств прямой задачи на величину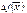

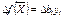
Экономико- математический анализ оптимальных решений базируется на свойсвах двойственных оценок  (для определения этих границ существует математические соотношения, которые реализованы в «Отчете по устойчивости» Excel. (теневые цены, интервалы устойчивости, допустимое увеличение, допустимое уменьшение)

Интервалы изменения объемов ресурсов ( компонент вектора В) в пределах которых двойственные оценки сохраняют свои значения принято называть интервалами устойчивости двойственных оценок.

Если двойственные оценки попадают в интервал устойчивости, то экономическое поведение не меняется Если выходят за пределы интервалов устойчивости ,то новое экономическое поведение получим в новом решении задачи.

1. те ограничения которые выполнялись как равенства , так и будут выполняться как равенства

2.структура плана останется неизменной

Совмещая  1 и 2  формируем новое поведение объемов ресурсов.

Двойственные оценки связаны с

оптимальным планом простой задачи .Всякое изменение исходных данных прямой задачи может оказать влияние как на ее оптимальный план (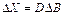) так и на систему оптимальных двойственных оценок. Поэтому чтобы проводить экономический анализ с использованием двойственных оценок,нужно знать их интервал устойчивости

10.Методы механического сглаживания временных рядов.  

Суть методов механического сглаживания заключается в следующем: берется несколько первых уровней временного ряда, образующих интервал сглаживания. Для них подбирается полином, степень которго должна быть меньше числа уровней, входящих в интервал сглаживания; с помощью полинома определяются новые, выравненные значения уровней в середине интервала сглаживания. Далее интервал сглаживания сдвигается на один уровень ряда вправо, вычисляется следующее сглаженно значение, и т.д.

Самым простым является метод простой скользящей средней.

Метод взвешенной скользящей средней

Метод экспоненциального сглаживания.

21.Постановка и экономико-математическая модель закрытой транспортной задачи.  

Имеется m пунктов производства однородного продукта с объемами производства  A1,A2,…,Am. Имеется n пунктов потребления этого продукта с объемами потребления b1,b2,…,bn. Известны оценки С= (Cij) M*N  транспортных затрат на перевозку единицы груза от i-того поставщика к j-тому потребителю (по коммуникации от i к j). Надо так прикрепить потребителей к поставщикам, чтобы минимизировать суммарные транспортные затраты на перевозку груза.  ЭММ ТЗ:  Обозначим через Xij, i=1,m  j=1,n объемы перевозок по коммуникации  i→j, т.е. в рассмотрение вводится матрица X=(Xij)m*n.


Min ∑ ∑ Cij Xij

∑ Xij = Ai,  i=1,m

∑ Xij = Bj,  j=1,n

 

Необходимым и достаточным условием разрешимости задачи является наличие баланса между спросом и предложением  ∑Ai = ∑Bj. Если имеется такое равенство, то ТЗ называется закрытой.

18.Оценка адекватности модели кривой роста. 

Трендовая модель считается адекватной, если правильно отражает систематические компоненты временного ряда. Это требование эквиваленто требованию, чтобы остаточная компонента 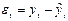 удовлетворяла свойствам случайной компоненты временного ряда.

1. Проверка случайности колебаний уровней остаточной последовательности можно проводить с помощью критерия пиков. Общее число поворотных точек для остаточной последовательности 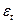 обозначим через p. В случайно выборке:

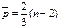- математическое ожидание числа точек поворота

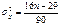 - дисперсия.

Критерием случайности с 5%-ным уровнем значимости является выполнение неравенства:

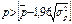
Если это неравенство не выполняется, трендовая модель считается неадекватной.

2. Проверка соответствия распределения случайной компоненты нормальному закону распределения.

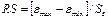Один из методов основан на RS-критерии. Этот критерий численно равен отношению размаха вариации случайной величины R к стандартному отклонению S.


Рассчетное значение RS-критерия сравнивается с табличными (критическими) нижней и верхней границами данного отношения, и если это отношение не попадает в интервал между критическими границами, то гипотеза о нормальности распределения отвергается. В противном случае принимается.

Для уровня значимости 0,05: n=10 (2,67;3,685). n=20 (3,18;4,49). n=30 (3,47;4,89).

3. Проверка равенства математического ожидания случайной компоненты нулю. Осуществляется на основе t-критерия Стьюдента. Расчетное значение задается формулой

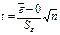, где 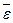 - ср. арифм. значение уровней ряда;  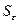- стандартное (среднеквадратическое) отклонение для этой последовательности. Если рассчетное значение t меньше табличного значения tα статистики Стьюдента с заданным уровнем значимости α и числом степеней свободы n-1, то гипотеза о равенстве нулю математического ожидания принимается. Если наоборот – отвергается модель считается неадекватной.

4. Проверка независимости значений уровней случайной компоненты.

Проверка отсутствия существенной автокорреляции в остаточной компоненте по критерию Дарбина-Уотсона. Рассчет ное значение этого критерия определяется по формуле

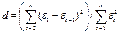
Вывод об адекватности трендовой модели делается, если все указанные выше 4 проверки свойств дают положительный результат.