Постановка задачи

При проведении статистического наблюдения за деятельностью предприятий корпорации получены выборочные данные по 32-м предприятиям, выпускающим однородную продукцию  (выборка 10%-ная, механическая), о среднегодовой стоимости основных производственных фондов и  о выпуске продукции за год.

В проводимом статистическом исследовании обследованные предприятия выступают как единицы выборочной совокупности, а показатели Среднегодовая стоимость основных производственных фондов и Выпуск продукции – как изучаемые признаки единиц.

Для проведения автоматизированного статистического анализа совокупности выборочные данные представлены в формате электронных таблиц процессора Excel в диапазоне ячеек B4:C35.

В процессе исследования совокупности необходимо решить ряд статистических задач для выборочной и генеральной совокупностей.

Статистический анализ выборочной совокупности

1.    Выявить наличие среди исходных данных резко выделяющихся значений признаков («выбросов» данных) с целью исключения из выборки аномальных единиц наблюдения.

2.    Рассчитать обобщающие статистические показатели совокупности по изучаемым признакам: среднюю арифметическую (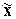), моду (Мо), медиану (Ме), размах вариации (R), дисперсию(σ²n), средние отклонения – линейное (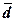) и квадратическое (σn), коэффициент вариации (Vσ), структурный коэффициент асимметрии  К.Пирсона (Asn).

3.    На основе рассчитанных показателей в предположении, что распределения единиц по обоим признакам близки к нормальному, оценить:

а) степень колеблемости значений признаков в совокупности;

б) степень однородности совокупности по изучаемым признакам;

в) устойчивость индивидуальных значений признаков;

г) количество попаданий индивидуальных значений признаков в диапазоны (), (), ().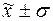

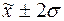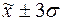4.    Дать сравнительную характеристику распределений единиц совокупности по двум изучаемым признакам на основе анализа:

а) вариации признаков;

б) количественной однородности единиц;

в) надежности (типичности) средних значений признаков;

г) симметричности распределений в центральной части ряда.

5.    Построить интервальный вариационный ряд и гистограмму распределения единиц совокупности по признаку Среднегодовая стоимость основных производственных фондов и установить характер (тип) этого распределения. Рассчитать моду Мо полученного интервального ряда и сравнить ее с показателем Мо несгруппированного ряда данных.

Статистический анализ  генеральной совокупности

1.               Рассчитать генеральную дисперсию 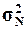, генеральное среднее квадратическое отклонение 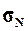 и ожидаемый размах вариации признаков R_N. Сопоставить значения этих показателей для генеральной и выборочной дисперсий.

2.               Для изучаемых признаков рассчитать:

а) среднюю ошибку выборки;

б) предельные ошибки выборки для уровней надежности P=0,683, P=0,954, P=0,997 и границы, в которых будут находиться средние значения признака генеральной совокупности при заданных уровнях надежности.

3.               Рассчитать коэффициенты асимметрии Asn и эксцесса Ek. На основе полученных оценок  сделать вывод о степени близости распределения единиц генеральной совокупности к нормальному распределению.

Априорный статистический анализ данных.

                                                                                                                                                       Таблица 1

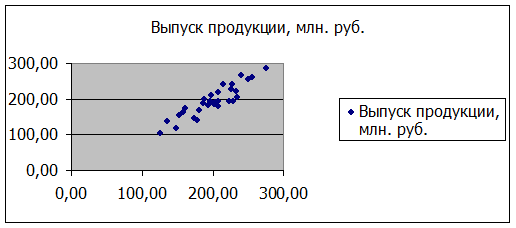
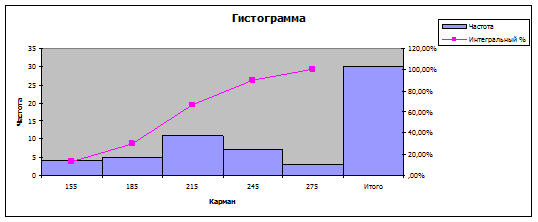
 Анализ выборочной совокупности.

1.    В результате проведенного исследования и данных таблицы 3 выявлено две аномальных  единицы наблюдения.

2.     С учетом данных таблиц 3 и 5 сформируем единую таблицу значений выборочных показателей табл. 8

«Описательные статистики выборочной совокупности.»

                                                                                                           Таблица 8                                   

3.а) Т.к. степень колеблемости признака определяется по значению коэффициента вариации Vσ , то исходя из оценочной шкалы Vσ > 60% мы можем сделать вывод, что колеблемость значений признаков в совокупности  значительная, т.к. и по первому, и по второму признакам мы имеем 538,51 >60%.

б) Т.К. 538,51  > 33%, то совокупность является количественно не однородной по данному признаку.

в) Сопоставление средних отклонений -  квадратического σ и линейного d позволяет сделать вывод об устойчивости индивидуальных значений признака, т.е. об отсутствии среди них «аномальных» вариантов значений.

Имеют место равенства :    σ = 1,25d    d = 0,8 σ.

σ =1,25*28,7=35,875;                  σ = 1,25*32,78=40,975;

d = 0,8*35,875=28,7;                    d = 0,8*40,975=32,78.

Отношение показателей может служить индикатором устойчивости данных :

d/σ =28,7/35,875=0,8 – для первого признака

     d/σ =32,78/40,975=0,8 - для второго признака.

     Т.к. соотношения равны 0,8, то значения признаков устойчивы, в них не   имеются « аномальные выбросы».    

г)Для нахождения количества попаданий индивидуальных значений признаков в диапазоны ( х±σ ),(х±2σ),(х±3σ) составим таблицу 9.

Распределение значений признака по диапазонам рассеяния признака относительно х.

                                                                                                                  Таблица 9

Из таблицы видно, что количество значений хi находящихся в данных диапазонах одинаково по обоим признакам и процентное соотношение равно: для (х±σn) – 71%, (х±2σn)  – 143%, (х±3σ) – 214 %.

4.а) Т.к. коэффициент вариации Vσ показывает интенсивность колеблемости признака, то на основе таблицы 5 сделаем вывод, что  Vσ  обоих признаков имеет одинаковое значение Vσ=538,516, следовательно Vσ>60%, следовательно колеблемость признака значительная.

б) Показатель Vσ служит индикатором совокупности, следовательно при выполнении условия Vσ<33% совокупность является количественно однородной , в нашем случае совокупность является не однородной .т.к. Vσ=538,513 >33%.

в) Так как оценка Vσ достаточно высока ,т.е. Vσ>40% (Vσ=538,513), то наблюдается значительное расхождение между значениями хi , т.е. средняя х ненадежная характеристика совокупности и ее практическое применение становится проблематичным.

г) Коэффициент К.Пирсона для признака «Среднегодовая стоимость основных произ-ных фондов» ASn  = -0,831,т.е. ASn <0, следовательно, здесь присутствует левосторонняя ассиметрия. Для  признака «Выпуск продукции»

ASn = -0,831 , т.е. ASn <0,следовательно ассиметрия – левосторонняя.

д) Значение моды М0  полученного интервального ряда данных находится дальше от значения средней арифметической , чем значение моды не сгруппированного ряда (207,5-200=7,5 ; 195-200=5).Это говорит о том , что кривая распределения полученного интервального ряда данных менее симметрична относительно оси симметрии , чем кривая распределения не сгруппированного ряда.

Анализ генеральной совокупности.

1.     На основе таблицы 3 сформируем отдельную таблицу для генеральных показателей σ²N,  σN, As, Eк .

                     « Описательная статистика генеральной совокупности »

                                                                                                                   Таблица 10.

Установим степень расхождения между σ²N  и  σ²n  по формуле :

σ²N  = n/n-1 * σ²n  

σ²N  =30/30-1*1272,45=1316,328             σ²N =30-30-1*1810,75=1873,792.

Рассчитаем прогнозные оценки вариации  RN  по следующей формуле:

                                                 RN =6σ.

RN =6*36,28=217,68

RN =6*43,28=259,68

Сравнивая прогнозные значения с Rn =150 , получим  150 < 217,68; 

180 <259,68 , т.е. RN > Rn.

По двум признакам прогнозная оценка размаха вариации в генеральной совокупности больше, чем в выборочной.

а) Средняя ошибка выборки  µx  рассчитана в таблице 3:

Для признака «Среднегодовая стоимость основных производственных фондов» µx = 6,624;

Для признака « Выпуск продукции» µx = 7,902.

б)Оценки предельных ошибок выборки имеются в таблицах 3,4а, 4б.На основе этих оценок и следующей формулы х-Δx≤ x ≤x+Δx сформируем следующую таблицу 11.

«Предельные ошибки выборки и ожидаемые границы для генеральных средних»

                                                                                                                                        Таблица 11

Для первого признака    200-6,745≤х≤200+6,745

                                             193,255≤х ≤ 206,745 и так далее.

Коэффициенты ассиметрии  Аs и процесса Ек имеются в таблице 10:

Аs = - 0,153                          Аs = 0,043

Ек = -0,345                           Ек =-0,205

Т.к    -0,153<0,25;       0,043<0,25,то ассиметрия распределения незначительная.

Т.к. -0,345<0 и -0,205<0, то это говорит о том, что вершина кривой распределения лежит ниже вершины нормальной кривой, в форма кривой более пологая по сравнению с нормальной. Это значит, что прямые формируются в центральной части и достаточно равномерно располагаются по всему диапазону от хмах до хмин..