Содержание
Задание
1. 3
Задание 2. 4
Задание 3. 5
Задание 4. 8
Задание 5. 10
Задание 6. 13
Список
использованной литературы.. 19
ВАРИАНТ 5
Задание
1
Имеется 11 билетов в театр, из которых 4 на места первого
ряда. По жребию разыгрываются три билета среди всех билетов. Найти вероятность
того, что среди выигравших билетов:
а) только один билет первого ряда;
b)
два билета первого ряда;
с) не менее двух билетов первого ряда;
d)
хотя бы один билет первого ряда;
е) все билеты либо первого, либо других рядов.
Решение:
N=11
всего билетов
n=4
из них на места первого ряда
m=3 наудачу
отобрано билетов
k-число
билетов на первый ряд среди трех выигравших
Используя формулу P(k)=Ckn*Cm-kN-n / CmN рассчитаем вероятности того, что среди выигравших билетов:
а) только один билет первого ряда:
P(k=1)=C14*C27 / C311 =
0,509
b)
два билета первого ряда
P(k=2)= C24*C17 / C311 = 0,255
с) не менее двух билетов первого ряда:
Р(k>=2)=Р(к=2)+Р(к=3)=
0,255+ C34*C07 / C311
=0,255+0,024=0,279
=0,3005
d)
хотя бы один билет первого ряда:
Р(k>=1)=1
- Р(к=0)=1 – C04*C37 / C311
=1-0,212=0,788
е) все билеты либо первого, либо других рядов:
Р(k=3
или k=0)= Р(к=0)+ Р(к=3)=0,212+0,024=0,236
Задание
2
Строительная бригада получает железобетонные
перекрытия от трех ДСК, причем ДСК-1 поставляет 31% всех перекрытий, ДСК-2 - 36%, а остальную продукцию
поставляет ДСК-3. Известно, что брак в продукции ДСК-1 составляет в среднем 8%,
ДСК-2 - 9%, а ДСК-3 - 10%. Для контроля качества из всех имеющихся перекрытий
наудачу берут два.
1. Определить вероятность того, что по крайней
мере одно из двух проверенных перекрытий будет иметь брак.
2. Оба проверенных перекрытия оказались без
брака. От каких ДСК вероятнее всего они поступили?
Решение:
А-отобранное изделие будет бракованным
В1-отобранное изделие получено от
ДСК-1
В2-отобранное изделие получено от
ДСК-2
В3-отобранное изделие получено от
ДСК-3
Р(В1)=0,31; Р(В2)=0,36;
Р(В3)=1-0,31-0,36=0,33;
Р1(А)=0,08; Р2(А)=0,09;
Р3(А)=0,1;
По формуле полной вероятности:
P(A)= Р(В1)* Р1(А)+ Р(В2)* Р2(А)+
Р(В3)* Р3(А)=
=0,31*0,08+0,36*0,09+0,33*0,1=0,0902
k-число бракованных перекрытий среди двух выбранных
1. Рассчитаем вероятность
того, что, по крайней мере, одно из двух проверенных перекрытий будет иметь
брак:
P(k≥1)=1 - P(k=0) = 1 - Ckn*pk*qn-k
=1 – C02 (0,0902)0*(1-0,0902)2 =
1 - 0,828 = 0,172
2. Событие С - отобранное изделие будет без
брака
Т.к. С противоположно А, то вероятность
события С равна:
Р(С) = 1 - P(A) = 1 - 0,0902 = 0,9098
Аналогично:
Р1(С)=1-0,08=0,92
Р2(С)=1-0,09=0,91
Р3(С)=1-0,1=0,9
Вероятность того, что перекрытие без брака
поступило от ДСК-1 по формуле Бейеса:
РС(В1) = Р(В1)
*Р1(С) / Р(С) = 0,31*0,92 / 0,9098 = 0,313
Вероятность того, что перекрытие без брака
поступило от ДСК-2:
РС(В2) = Р(В2)
*Р2(С) / Р(С) = 0,36*0,91 / 0,9098 = 0,360
Вероятность того, что перекрытие без брака
поступило от ДСК-3:
РС(В3) = Р(В3)
*Р3(С) / Р(С) = 0,33*0,9 / 0,9098 = 0,326
Итак, вероятнее всего, что перекрытия без
брака поступили от ДСК-2.
Задание
3
Некоторая страховая компания выплачивает
страховую сумму в среднем по 6% договоров.
1. Какова вероятность того, что среди 400 клиентов
данной страховой компании доля получивших страховую сумму будет:
a) равна 4%;
b) не менее 4%;
c) не более 11%;
d) не менее 3%,
но не более 9%?
2. Сколько нужно
застраховать клиентов, чтобы с вероятность 0,95 можно было утверждать, что доля
получивших страховую сумму среди них отклонится по абсолютной величине от
вероятности получения каждым клиентом страховой суммы не более, чем на 0,02?
Решение:
1.p=0,06 - вероятность получения страховки
q=1-0,06=0,94 – вероятность не получения страховки
1. n=400 – число выбранных
клиентов
k – число клиентов, получивших страховку среди выбранных
Используя формулу Бернулли Pn(k)=Ckn*pk*qn-k рассчитаем
вероятности того, что доля получивших страховую сумму будет:
a) равна 4%:
4% из 400 клиентов составляет:
k=0,04*400=16
Р(k=16)= C40016*0,0616*0,94384=0,0205
b) не менее 4%:
4%*400=16
Р(k≥16)=Р(16, 400)
Воспользуемся интегральной теоремой Лапласа:
P(k1, k2)=Ф(x2)-Ф(x1)
где Ф(x) - функция Лапласа[1]
x1=(k1-n*p)/√npq=(16-400*0,06)/√400*0,06*0,94=
-1,68
x2=(k2-n*p)/√npq=(400-400*0,06)/√400*0,06*0,94=
79
Ф(-1,68)= -0,4535
Ф(79)= 0,5
Значит:
P(16, 400)= -0,4535+0,5=0,
Тогда искомая вероятность равна:
Р(k≥16)=1-Р(0,16)=1-0,2776=0,0465
c) не более 11%:
11%*400=44
Р(k≤44)=Р(0,44)
Решение аналогично пункту b), но:
x2=(k2-n*p)/√npq=(44-400*0,06)/√400*0,06*0,94=
4,21
Ф(4,21)= 0,499968
Значит:
Р(k≤44)=P(0,44)= 0,499968+0,5=0,999968
d) не менее 3%,
но не более 9%:
0,03*400=12
0,09*400=36
P(12, 36)=Ф(x2)-Ф(x1)
x1=(k1-n*p)/√npq=(12-400*0,06)/√400*0,06*0,94=
-2,526
x2=(k2-n*p)/√npq=(36-400*0,06)/√400*0,06*0,94=
2,526
Ф(-2,526)= -0,4941
Ф(2,526)= 0,4941
Значит:
P(12,36)= 0,4941+0,4941=0,9882
2. Воспользуемся формулой:
Р(│m/n - p│≤ε)=2Ф(ε*√(n/pq))
ε=0,02
Р=0,95
Р(│m/n – 0,06│≤0,02)=2Ф(0,02*√(n/0,06*0,94))=0,95
Ф(0,02*√(n/0,06*0,94))=0,475
0,02*√(n/0,06*0,94)=1,96
√(n/0,06*0,94))=98
n/0,06*0,94=9604
n=541,67=542
Значит, нужно застраховать 542 клиента.
Задание 4
Для сигнализации об аварии в офисе некоторой фирмы города N
установлено три сигнализатора различных типов, которые работают независимо друг
от друга. Во время аварии сигнализаторы первого типа не срабатывают в среднем в
3%, второго - 4%,
третьего - 3% всех аварийных случаев. Рассматривается случайная величина (с.в.)
ξ - число сигнализаторов, сработавших во время аварии.
1. Составить ряд распределения с.в. ξ и представить его
графически.
2. Найти функцию распределения с.в. ξ и построить его
график.
3. Вычислить математическое ожидание (среднее значение) М
ξ, дисперсию D
ξ и среднее квадратическое (стандартное) отклонение σ (ξ).
4. Определите вероятности:
а) Р {ξ < М ξ };
b) Р
{ξ < М ξ +1};
c) Р
{|ξ - М ξ| < σ (ξ)}.
Решение:
1. q1=0,03; q2=0,04; q3=0,03;
p1=0,97;
p2=0,96; p3=0,97;
Р (ξ =0) = 0,03*0,04*0,03=0,00004
Р (ξ =1) = 0,97*0,04*0,03+0,03*0,96*0,03+0,03*0,04*0,97=0,00319
Р (ξ =2) = 0,97*0,96*0,03+0,03*0,96*0,97+0,97*0,04*0,97=0,09351
Р (ξ =3) = 0,97*0,96*0,97=0,90326
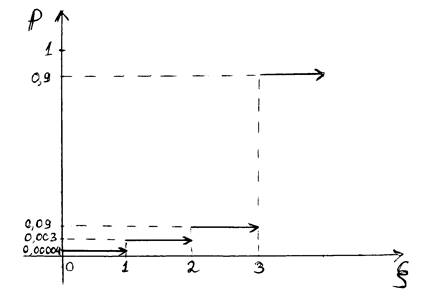
Ряд распределения с.в. ξ:
|
ξ
|
Р
|
|
0
|
0,00004
|
|
1
|
0,00319
|
|
2
|
0,09351
|
|
3
|
0,90326
|
|
|
1
|
и его графическое представление:
2. Функция распределения с.в. ξ:
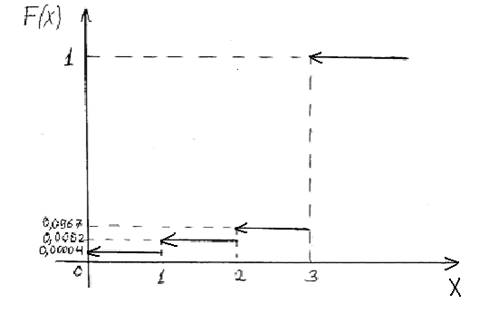
F(x)=P(X-x)
|
F(x)
|
x
|
|
0
|
x<=0
|
|
0,00004
|
0<x<=1
|
|
0,00323
|
1<x<=2
|
|
0,09674
|
2<x<=3
|
|
1
|
x>3
|
Его графическое представление:
3.
|
ξ
|
Р
|
ξ *Р
|
ξ2
|
ξ2* Р
|
|
0
|
0,00004
|
0
|
0
|
0
|
|
1
|
0,00319
|
0,00319
|
1
|
0,00319
|
|
2
|
0,09351
|
0,18702
|
4
|
0,37403
|
|
3
|
0,90326
|
2,70979
|
9
|
8,12938
|
|
Сумма:
|
1
|
2,9
|
-
|
8,5066
|
Математическое ожидание (среднее значение):
М ξ=∑ξ *Р=2,9
Дисперсия:
D
ξ= М (ξ2) – (М ξ)2=∑ ξ2* Р - (М ξ)2=8,5066-2,92=0,0966
Среднее квадратическое (стандартное отклонение):
σ(ξ)=√Dξ=√0,0966=0,3108
4. а) Р {ξ < М ξ }= Р
{ξ < 2,9}= Р (ξ =0)+ Р (ξ =1)+ Р (ξ =2)= 0,096736
b) Р
{ξ < М ξ +1}= Р {ξ < 3,9}= Р (ξ =0)+ Р (ξ =1)+ Р
(ξ =2)+Р (ξ =3)=1
c) Р
{|ξ - М ξ| < σ (ξ)}= Р {|ξ – 3,9| < 0,3108}= Р
(ξ =4)=0
Задание 5
Время ξ (в днях), через которое поставщик начинает поставлять
свою продукцию после подписания контракта, является случайным с плотностью
распределения
p(x)=
С(7-х)4 , если 0≤x≤7
0, в противном случае
1. Установить неизвестную постоянную
С и построить график функции p(x).
2. Найти функцию распределения с.в.
ξ и построить ее график.
3. Вычислить математическое ожидание
(среднее значение) М ξ, дисперсию D ξ и среднее квадратическое
(стандартное) отклонение σ (ξ).
4. Во сколько раз число поставок с
временем поставки меньше среднего превышает число поставок с временем поставки выше
среднего?
Решение:
1. Для определения коэффициента С
воспользуемся формулой:
-∞+∞∫f(x)dx=1
Так как f(x) на разных интервалах задана различными выражениями, то
интеграл -∞+∞∫f(x)dx
разбиваем на два интервала:
-∞+∞∫f(x)dx=-∞0∫0dx+07∫С(7-х)4
dx+7∞∫0dx =1
Отсюда 07∫ С(7-х)4
dx =1
-1/5*С*(7-х)5│07=1
75/5*С=1
Следовательно: С=5/75
В силу этого плотность
вероятности запишется:
0, если x<0
p(x)=
5/75*(7-х)4 , если 0≤x≤7
0, если x>7
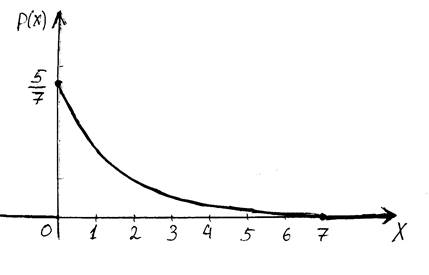
2. Чтобы найти функцию распределения
с.в. ξ используем формулу:
F(x)= -∞x∫f(x)dx
Если x<0, то f(x)=0, следовательно,
F(x)= -∞x∫0dx=0
Если 0≤x≤7, то
F(x)= -∞0∫0dx + 0x∫5/75*(7-х)4
dx= 0x∫5/75*(7-х)4
dx =
-(1-x/7)5│0x=(1-x/7)5
Если x>7, то:
F(x)= -∞0∫0dx + 07∫5/75*(7-х)4
dx+7х∫0dx=-(1-x/7)5│07=1
Итак:
0, если x<0
F(x)= (1-x/7)5, если 0≤x≤7
1, если x>7
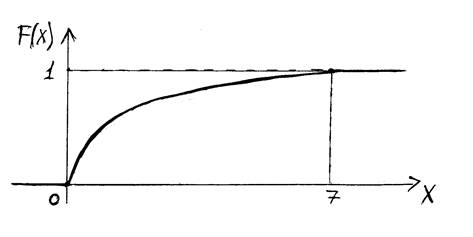
3. Воспользуемся формулами:
M(X)= -∞+∞∫x*f(x) dx и D(X)= -∞+∞∫x2*f(x) dx – [M(X)]2;
M(X)= -∞+∞∫x*f(x) dx=-∞0∫0*хdx+07∫5/75*(7-х)4
хdx+7+∞∫0*хdx =
=-х(1-х/7)5-(7-х)6/6*75│07=7/6
D(X)= -∞+∞∫x2*f(x) dx – 7/62=-∞0∫x2*0dx+07∫5/75*(7-х)4
х2 dx+7+∞∫0*х2
dx -7/62=
-х2(1-х/7)5-х(7-х)6/3*75
-(7-х)7/3*76│07-7/62=7/3-7/62=0,972
Cреднее квадратическое (стандартное) отклонение σ (ξ):
σ
(x)= √D(X)=0,986
4. Определим вероятность того, что
время поставки будет меньше среднего (M(x)=7/6):
p(ξ<7/6)=
07/6∫5/75*(7-х)4 dx=-(1-x/7)5│07/6=1-(5/6)5
И вероятность того, что время
поставки будет выше среднего:
p(ξ>7/6)=7/6∞∫5/75*(7-х)4
dx=-(1-x/7)5│7/6∞=(5/6)5
n=(1-5/65) / (5/6)5=(6/5)5-1=1,48832
Итак, число поставок с временем
поставки меньше среднего превышает число поставок с временем поставки выше
среднего приблизительно в 1,5 раз.
Задание
6
При штамповке шариков для подшипников происходят
случайные отклонения диаметров шариков от номинала. При обследовании 25 шариков
эти отклонения составили (в мм):
-0.567, -0.221, 0.027, -0.255, -0.141, 0.231, 0.093,
0.173, -0.494,-0.473, -0.472, -0.174, -0.562, -1.216, 0.546, 0.338, 0.061, -0.430,
-0.397, -0.376, 0.119, -0.172, 0.557,-0.590, 0.163
Необходимо:
1.
Определить исследуемый признак и его тип (дискретный или непрерывный).
2. В
зависимости от типа признака построить полигон или гистограмму относительных
частот.
3. На
основе визуального анализа полигона (гистограммы) сформулировать гипотезу о
законе распределения признака.
4.
Вычислить выборочные характеристики изучаемого признака: среднее, дисперсию,
среднее квадратическое (стандартное) отклонение.
5.
Используя критерий согласия «хи-квадрат» Пирсона, проверить соответствие
выборочных данных выдвинутому в п.3 закону распределения при уровне значимости
0,05.
6.
Для генеральной средней и дисперсии построить доверительные интервалы,
соответствующие доверительной вероятности 0,95.
7. С
надежностью 0,95 проверить гипотезу о равенстве:
а)
генеральной средней значению 0,749;
б)
генеральной дисперсии значению 0,183.
Решение:
1. Тип исследуемого признака непрерывный, т.к. все значения
встречаются ровно по одному разу и распределены в интервале от -1,216 до 0,557мм
2. Т.к. тип признака непрерывный, то весь интервал, в
котором заключены все наблюдаемые значения признака разобьем на ряд частичных
интервалов. Оптимальное количество интервалов равно 10. Найдем длину интервалов
h:
h= (xmax - xmin) / 10 =
(0,557 – (-1,216)) / 10 = 0,18
Округляя это вычисленное значение получим длины интервалов h=0,2 и найдем mi – количество значений, попавших в i-й интервал:
|
Номер интервала
i
|
Частичный
интервал
xi-1 - xi
|
Частоты
mi
|
Относительные
частоты
wi= mi /∑mi
|
Плотности относительных частот
wi/h
|
|
1
|
< -0,6
|
1
|
0,04
|
0,2
|
|
2
|
-0,6 - -0,4
|
7
|
0,28
|
1,4
|
|
3
|
-0,4 - 0,2
|
4
|
0,16
|
0,8
|
|
4
|
-0,2 - 0
|
3
|
0,12
|
0,6
|
|
5
|
0 - 0,2
|
6
|
0,24
|
1,2
|
|
6
|
0,2 - 0,4
|
2
|
0,08
|
0,4
|
|
7
|
0,4 - 0,6
|
2
|
0,08
|
0,4
|
|
8
|
>0,6
|
0
|
0
|
0
|
|
Сумма:
|
-
|
25
|
1
|
|
Построим гистограмму:
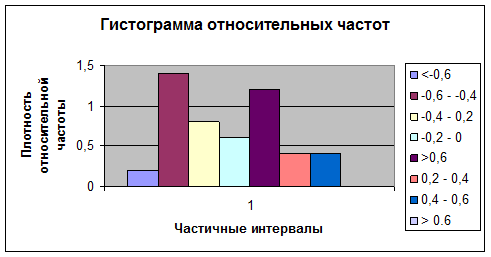
3. На основе
визуального анализа гистограммы можно сделать предположение о нормальном распределении признака, т.е.:
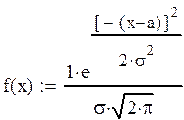
где а –
математическое ожидание, σ
– среднее квадратическое ожидание.
4. Серединные
значения интервалов рассчитаны как xi*= (xi+ xi-1)/2
|
Номер интервала
i
|
Середины
частичных интервалов
xi*
|
Частоты
mi
|
xi**mi
|
xi* 2
|
xi* 2* mi
|
|
1
|
-0,7
|
1
|
-0,7
|
0,49
|
0,49
|
|
2
|
-0,5
|
7
|
-3,5
|
0,25
|
1,75
|
|
3
|
-0,3
|
4
|
-1,2
|
0,09
|
0,36
|
|
4
|
-0,1
|
3
|
-0,3
|
0,01
|
0,03
|
|
5
|
0,1
|
6
|
0,6
|
0,01
|
0,06
|
|
6
|
0,3
|
2
|
0,6
|
0,09
|
0,18
|
|
7
|
0,5
|
2
|
1
|
0,25
|
0,5
|
|
8
|
0,7
|
0
|
0
|
0,49
|
0
|
|
|
|
25
|
-3,5
|
|
3,37
|
Вычислим выборочные характеристики изучаемого
признака: среднее значение (MX)
, дисперсию, среднее квадратическое (стандартное) отклонение:
xсрвыб = ∑ xi**mi /n=-3,5/25= -0,14
Dвыб= x*2cp
-xсрвыб 2=∑ xi*2* mi / n - xсрвыб 2=3,37/25-0,142=0,1152
σвыб=√0,1152=0,3394
5. Найдем
исправленную выборочную дисперсию s2:
s2=n/n-1 * Dвыб=25/24 * 0,1152=0,12
и исправленное
выборочное среднее квадратическое отклонение:
s=0,3464
Найдем
теоретические частоты mi′:
mi′=n*h/s *φ(ti*)=25*0,2/0,3464*φ(ti*)=14,4338*φ(ti*),
где ti*= (xi*- xсрвыб)/s
Составим расчетную таблицу
для нахождения теоретических частот:
|
i
|
xi*
|
ti*= (xi*- xсрвыб)/s
|
φ(ti*)[2]
|
mi′=n*h/s *φ(ti*)
|
|
1
|
-0,7
|
-1,62
|
0,11
|
1,55
|
|
2
|
-0,5
|
-1,04
|
0,23
|
3,35
|
|
3
|
-0,3
|
-0,46
|
0,36
|
5,18
|
|
4
|
-0,1
|
0,12
|
0,40
|
5,72
|
|
5
|
0,1
|
0,69
|
0,31
|
4,54
|
|
6
|
0,3
|
1,27
|
0,18
|
2,57
|
|
7
|
0,5
|
1,85
|
0,07
|
1,04
|
|
8
|
0,7
|
2,42
|
0,02
|
0,31
|
Затем составим расчетную таблицу для вычисления наблюдаемого
значения критерия χ2набл.:
|
i
|
mi
|
mi′
|
mi - mi′
|
(mi - mi′)2
|
(mi - mi′)2/ mi′
|
|
1
|
1
|
1,55
|
-0,55
|
0,30
|
0,20
|
|
2
|
7
|
3,35
|
3,65
|
13,30
|
3,97
|
|
3
|
4
|
5,18
|
-1,18
|
1,39
|
0,27
|
|
4
|
3
|
5,72
|
-2,72
|
7,38
|
1,29
|
|
5
|
6
|
4,54
|
1,46
|
2,14
|
0,47
|
|
6
|
2
|
2,57
|
-0,57
|
0,33
|
0,13
|
|
7
|
2
|
1,04
|
0,96
|
0,92
|
0,88
|
|
8
|
0
|
0,31
|
-0,31
|
0,09
|
0,31
|
|
∑
|
-
|
-
|
-
|
-
|
χ2набл =7,51
|
По таблице критических точек распределения χ2кр(α,s)[3] при заданном уровне
значимости α=0,05 и числе степеней свободы s=k-3=8-3=5 находим критическую точку правосторонней критической
области:
χ2кр=
χ2кр(0,05;5)=11,1
Так как χ2набл < χ2кр,
то по данным выборки нет оснований отвергать гипотезу о нормальном
распределении признака X
в генеральной совокупности.
6. Т.к.
генеральная совокупность распределена нормально, то для построения
доверительного интервала генеральной средней можно воспользоваться формулой:
xсрвыб - tγ(s/√n)< xсрген< xсрвыб + tγ(s/√n),
где
s - исправленное выборочное среднее квадратическое
отклонение, равное 0,3464 (см. п.5);
tγ находят по таблице[4] по заданным n и γ
γ=0,95 (по условию)
t(0.95, 25)=2,064
tγ*(s/√n)=
2,064*0,3464/√25=0,14
xсрвыб = -0,14 (см. п.4)
Тогда искомый интервал имеет
вид:
-0,14-0,14< xсрген<-0,14+0,14
-0,28< xсрген<0
Чтобы построить доверительный интервал генеральной дисперсии
сначала найдем доверительный интервал среднего квадратического отклонения по
формуле:
s(1-q) <σген< s(1+q) (при q<1),
0< σген< s(1+q)
(при q>1),
где q
находят по таблице[5]
по данным n и γ
q(0.95, 25)=0,32
Доверительный интервал среднего квадратического отклонения:
0,3464*(1-0,32) <σген<0,3464*(1+0,32)
0,2356<σген<0,4572
Тогда доверительный интервал генеральной дисперсии имеет
вид:
0,23562<Dген<0,45722
0,0555<Dген<0,2091
7. а) Т.к. доверительный интервал генеральной средней -0,28< xсрген<0 не
включает значение 0,749,
то с надежностью 0,95 можно отвергнуть гипотезу.
б) Т.к. доверительный интервал генеральной дисперсии 0,0555<Dген<0,2091 включает
значение 0,183, то с надежностью 0,95 можно утверждать о правильности гипотезы.
Список
использованной литературы
1.
Гмурман В.Е./ Теория вероятностей и математическая
статистика. М.: Высшая школа, 2002
2.
Гмурман В.Е./ Руководство к решению задач по теории
вероятностей и математической статистике. М.: Высшая школа, 2002
3.
Колемаев В.А., Староверов О.В., Турундаевский В.Б./
Теория вероятностей и математическая статистика. М.: Высшая школа, 1991
4.
Семенов А.Т. /Теория вероятностей и математическая
статистика: Учебно-методический комплекс. – Новосибирск: НГАЭиУ, 2003
5.
Семенов А.Т. /Теория вероятностей: Учебное пособие. –
Новосибирск: НГАЭиУ, 2003
[1]
Гмурман В.Е. Руководство к решению задач по теории вероятностей и
математической статистике. М.: Высшая школа, 2002. Прил. 2, С. 390.
[2]
Гмурман В.Е. Руководство к решению задач по теории вероятностей и
математической статистике. М.: Высшая школа, 2002. Прил. 1, С. 388.
[3]
Гмурман В.Е. Руководство к решению задач по теории вероятностей и
математической статистике. М.: Высшая школа, 2002. Прил. 5, С. 393.
[4]
Гмурман В.Е. Руководство к решению задач по теории вероятностей и
математической статистике. М.: Высшая школа, 2002. Прил. 3, С. 392.
[5]
Гмурман В.Е. Руководство к решению задач по теории вероятностей и
математической статистике. М.: Высшая школа, 2002. Прил. 4, С. 392.