Задание 1

         Высказано утверждение: «Размер заработной платы зависит от пола работника». Как можно  проверить это утверждение?

         Данное утверждение   можно связать с производительностью труда  мужчин и женщин.  Предположим, что   мужчина и женщина выполняют одну и ту же  физическую работу, которая оплачивается сдельно, то есть в зависимости от количества произведенной продукции. Мужчина   в силу своей выносливости  может выполнить  больший  объем работ, чем женщина. Соответственно  объем произведенной им продукции будет намного выше, чем у женщине. А соответственно,  размер заработной платы будет выше . чем у женщины.

Задание 2

На рисунках 1 и 2  приведены результаты анализа   распределения заработной платы на двух предприятиях. Что вы  можете сказать об этих распределениях? Какие  показатели можно использовать для   их описания? Какие показатели  вы можете оценить, опираясь только на приведенные  рисунки ( абсолютные  значения, знаки, в сравнении друг с другом…)?

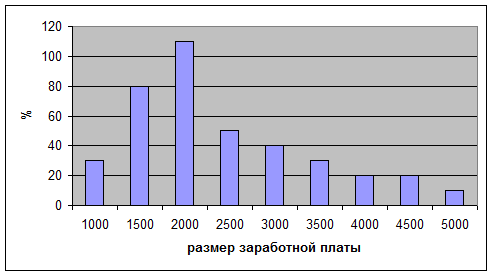
Рис. 1. Распределение зарплаты  по предприятию 1

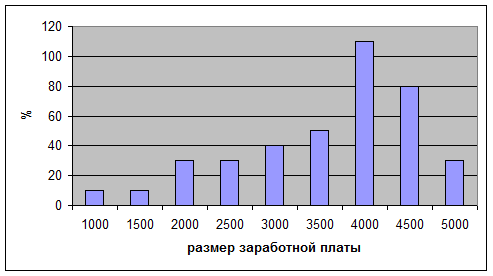
Рис. 2. Распределение зарплаты по предприятию 2

РЕШЕНИЕ

1) Как видно из рисунка 1, на 1 предприятии  максимальное значение показателя  частоты соответствует  размеру значения  заработной платы –2000 рублей, а минимальное – размеру зарплаты -  5000 руб. Рисунок 1 свидетельствует о том, что  минимальным значениям заработной платы ( в пределах от  1000 до 2500 руб. соответствуют наибольшие  частоты,  при зарплате  свыше 2500 руб. - частоты наименьшие.   В целом  можно сделать вывод, что в организации  наблюдается    невысокий уровень заработных плат в целом по всем работникам.

2) Как видно из рисунка 2,  на предприятии 2 максимальное значение  показателя частоты соответствуют наибольшим значениям заработной платы: при частоте  110 % заработная плата максимальна  и равна  4000 руб. Минимальные значения заработной платы имеют  низкие значения частоты  в пределах от 2 до 5. В целом на предприятии наблюдается тенденция  высоких заработных плат и хорошей оплачиваемости труда.

         Опираясь на данные рисунки , можно оценить следующие показатели:

1)     динамика заработной платы,

2)     частота

Задание 3

         Высказано утверждение: «Размер заработной платы зависит от стажа работы». Как облечь это утверждение в форму эконометрической модели? Как можно проверить это утверждение?

         Дело в том, что  в большинстве случав при расчете заработной платы используется  надбавка за выслугу лет, которая представляет собой коэффициент, увеличивающий размер заработной платы.  Чем выше стаж работы и выслуга лет, тем выше  коэффициент. Так , например, при стаже 1 год  коэффициент равен 1,1 , при стаже 2 года этот коэффициент растет до 1,2 и так далее. Таким образом, очевидно, что  при росте стажа работы увеличивается коэффициент и, соответственно, размер заработной платы.

Задание 4

         Имеются данные о времени доставки  продукции на различные расстояния. Был проведен анализ, результаты которого  приведены на рисунке 3. Подробно объясните, что проделал исследователь, что получилось в результате и как эти результаты  можно использовать?

Таблица 1

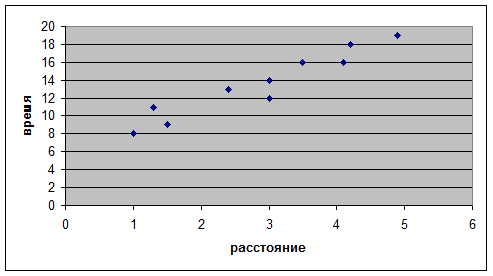
Рис. 3. Результаты анализа

РЕШЕНИЕ

         Последовательность действий исследователя:

1) предположение о наличии линейной зависимости между показателями  времени доставки (х) и   расстоянием доставки (у) типа у = кх +В

2) определение значения коэффициентов к и в методами корреляционно- регрессионного анализа

3)     определение уравнения зависимости  у = 2, 6597 х+5,9135

4)     расчет коэффициента корреляции равного 0,9183, показывающего тесноту связи между показателями

Необходимо расчета коэффициента корреляции заключается в рассмотрении тесноты связи меду показателями. Необходимость  определения  формулы зависимости между показателями заключается в возможности дальнейшего прогнозирования исследуемых значений.

Задание 5

Приведите данные, касающиеся вашей работы, для которых можно использовать метод, приведенный в задании 4. Опишите содержательную задачу, ожидаемый результат и как его можно использовать?

Условие задачи:

На основании приведенных данных построить линейное уравнение зависимости уровня издержек обращения от запасов товаров. Определить коэффициент корреляции.

Таблица 2

Решение:

1)    Принимаем величину запасов товаров за переменную х, а величину уровня издержек за переменную y. Тогда значения х_ср и y_ср определяем по формулам (1) и (2):

х_ср = (Σ x_i) / n,                      (1)

y_ср = (Σ y_i) / n,                      (2)

где    n = 5,

         i = 1…5

Тогда, х_ср = 400: 5 = 80

           y_{ср =}  132 : 5 = 26,4

2)    Дальнейшие результаты расчета представляем в виде таблицы 3

Таблица 3

Σ(x_i - х_ср)² = 186

Σ(y_i - y_ср)² = 8,54

Σ(x_i - х_ср)( y_i - y_ср) = 39,7

3)    Теснота связи между показателями уровня издержек и запасов товаров измеряется коэффициентом корреляции, который исчисляется по формуле (3):

V = δ²_xy / δ_x · δ_y,                                      (3)

где    V – коэффициент корреляции,

δ_x =  [Σ(x_i - х_ср)²/ n]^1\2,                           (4)

δ_y =  [Σ(y_i - y_ср)²/ n]^1\2,                           (5)

δ²_xy = 1/n ∑ (x_i - х_ср)( y_i - y_ср),              (6)

Подставляя имеющиеся значения  в формулы (4),(5),(6),получаем:

δ_x = (186/5)^1/2 = (37,2)^1/2 = 6,1

δ_y = (8,54/5)^1/2 = (1,708)^1/2 = 1,31

δ²_xy = 39,7/5 = 7,94

Тогда, значение коэффициента корреляции равно:

V = 7,94/ (6,1· 1,31) ≈ 0,994

4)    Считая формулу связи между уровнем издержек и запасом товаров линейной (y = a₀ + a₁x), определим зависимость уровня издержек от запасов товаров. Для этого решается система нормальных уравнений:

na₀ + a₁∑x_i = ∑y_i,                          (7)

a₀∑x_i + a₁∑x_i² = ∑ x_i y_i,                      (8)

Величины ∑x_i² и ∑ x_i y_i представлены в таблице 4.

Таблица 4

         Значение a₀ определяем из формулы (7):

5 a₀ + 400 a₁ = 132,

400 a₀ + 32186 a₁ = 10599,7

a₀ = (132 – 400  a₁)/ 5,

или a₀ = 26,4 – 80 a₁

         Подставляя найденное значение a₀  в формулу (8), находим значение a₁:

400 (26,4 – 80 a₁) + 32186 a₁ = 10599,7

10560 – 32000 a₁ + 32186 a₁ = 10599,7

186 a₁ = 39,7

a₁ = 0,21

Тогда, a₀ = 26,4 - 80 * 0,21 = 9,6.

         Итак, уравнение регрессии в окончательном виде имеет следующий вид:

y_ср = 9,6 + 0,21 · x_ср

5)    Проведем проверку, подставляя значение x_ср в полученное уравнение зависимости:

y_ср = 9,6 + 0,21 * 80 = 26,4.

Полученное значение y_ср соответствует выше рассчитанному значению.

Ответ: 1) коэффициент корреляции равен 0,994

             2) уравнение зависимости уровня издержек обращения от запасов товаров имеет вид: y_ср = 9,6 + 0,21 · x_ср

Задание 6

Имеются данные  о динамике выпуска продукции неким предприятием. На рисунке 4 приведены результаты анализа. Подробно объясните, что проделал исследователь, что получилось в результате и как эти результаты можно использовать?

Таблица 5

Исходные данные

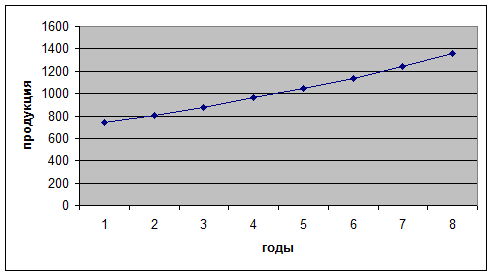
Рис. 4. Динамика продукции

У = 677,64е^0,0866х

R ² = 0,9999

РЕШЕНИЕ

Последовательность действий исследователя:

1) предположение о наличии нелинейной зависимости между показателями  года (х) и   продукцией (у)

2) определение уравнения зависимости У = 677,64е^0,0866х

3) расчет коэффициента корреляции равного 0,9999, показывающего тесноту связи между показателями

Необходимо расчета коэффициента корреляции заключается в рассмотрении тесноты связи меду показателями. Необходимость  определения  формулы зависимости между показателями заключается в возможности дальнейшего прогнозирования исследуемых значений.

Задание 7

Имеются данные  о динамике продаж некоторой продукции. На рисунке 5 приведены результаты анализа. Подробно объясните, что проделал исследователь, какие методы  можно применить, что получилось в результате и как эти результаты можно использовать?

Таблица  6

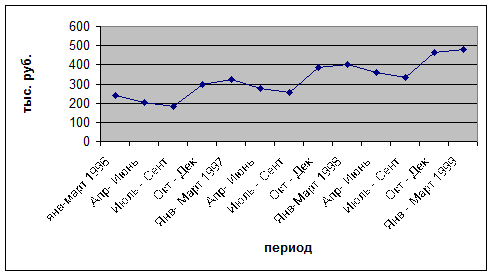
Рис. 5. Динамика реализации продукции

У = 20,978х+176,31

R 2 = 0,7666

РЕШЕНИЕ

         Последовательность действий исследователя:

1) предположение о наличии линейной зависимости между показателями  времени  (х) и   реализации (у) типа у = кх +В

2) определение значения коэффициентов к и в методами корреляционно- регрессионного анализа

3)    определение уравнения зависимости  У = 20,978х+176,31

4)    расчет коэффициента корреляции равного 0,7666, показывающего тесноту связи между показателями

Необходимо расчета коэффициента корреляции заключается в рассмотрении тесноты связи меду показателями. Необходимость  определения  формулы зависимости между показателями заключается в возможности дальнейшего прогнозирования исследуемых значений.

Задание 8

Приведите данные, касающиеся вашей работы, для которых можно  использовать метод, приведенный в задании 7. Опишите содержательную  задачу, ожидаемый результат, и как его можно использовать?

РЕШЕНИЕ

Исходные данные задачи представлены в таблице 4, где Х - готовая продукция на складе предприятия, У – выручка от реализации продукции.

РЕШЕНИЕ

1)    Найдем параметры уравнения регрессии методом наименьших квадратов.

Предполагается наличие линейной  связи между Х и У, то есть регрессионная модель описывается функцией:

У_i’ = а₀ + а₁ х,                        (9)

где    У_i’ – значение результативного признака;

         а₀  и а₁ – параметры уравнения регрессии, определяемые из системы уравнений:

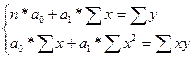,                          (10)

         Для нахождения параметров уравнения регрессии по методу наименьших квадратов, составим расчетную таблицу (таблица 7)

Таблица 7

Расчетная таблица для нахождения параметров уравнения регрессии

         Подставляем полученные значения из таблицы 7 в формулу (10):

         Из первого уравнения выражаем а₀, подставляем во второе уравнение и получаем соответствующее значение:

а₁ = 0,27 и а₀ = 1,33

         Тогда искомое уравнение регрессии имеет вид:

У_i’= 1,33 + 0,27Х.

2)    Для проверки адекватности определим среднее относительное линейное отклонение по формуле (11)

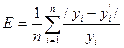,                          (11)

     Подставляя значения из таблицы 7 в формулу (11), получим:

Е = 0,10 или 10 %.

     Так как Е меньше 15 %, то связь между факторным и результативным признаками достаточно тесная.

     Полученное уравнение регрессии пригодно для прогнозных значений, так как значение Е меньше 15 %.

         Среднегодовое значение Х = 24,43 млн. руб., тогда при среднегодовой величине готовой продукции на сладе 24, 43 млн. рублей, предполагаемая выручка от реализации на следующий год, согласно уравнению регрессии, составит: 7,93 млн. рублей.