Содержание
Задача1. 3
Задача 2. 4
Задача 3. 4
Задача 4. 4
Задача 5. 6
Задача 6. 7
Задача 7. 9
Задача 8. 10
Список
литературы.. 11
Задача1
Фирма может выпускать два товара: x, y. Функция выпуска товара y имеет вид:
y=-x2-6x+160
Определите альтернативную стоимость выпуска товара x и постройте график
производственных возможностей выпуска товаров x, y.
Решение:
Для того, чтобы определить альтернативную стоимость выпуска
товара x, выразим x через
y:
-x2-6x+160-y=0
x2+6x-(160-y)=0
Итак альтернативная стоимость выпуска товара x выглядит следующим образом:
x=-3+(169-y)1/2
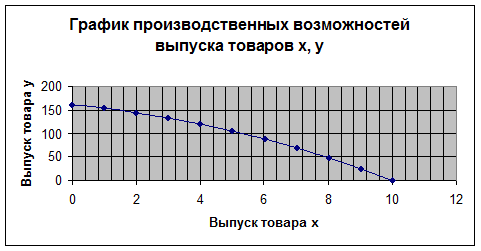
Из уравнений y=-x2-6x+160 и x=-3+(169-y)1/2 можно сделать вывод о
том, что при x=0 выпуск
товара y будет равен
160 ед., а при y=0
выпуск товара x будет
равен 10 ед.
Теперь построим график производственных возможностей выпуска
товаров x, y:
Задача 2
Функция полезности имеет вид: TU=(4Qx, Qy).
Доход покупателя (I)
равен 24 руб. Он покупает 2 ед. товара x и 3 ед. товара y.
Найти (Px, Py).
Решение:
Покупатель оптимизирует свой выбор при условии равенства
предельных полезностей этих благ:
Qx/ Px = Qy/ Py
Qx/ Px = 4Qx
/ Py
Py =4*Px
Доход покупателя должен позволить купить 2 ед. товара x и 3 ед. товара y, т.е.:
I ≥ 2*Px
+ 3*Py
24 ≥ 2*Px
+ 3*(4*Px)=14 Px
Px=1 руб.
Py =4 руб.
Значит (Px,
Py)=( 1 руб, 4 руб.)
Задача 3
Пусть Edp=-2.
Цена товара снизилась с 30 руб. до 20 руб. за ед. На сколько процентов
увеличился объем продаж.
Решение:
Edp=∆Q/Q0 : ∆P/P0
∆Q/Q0 =∆P/P0 * Edp=(20-30)/30 * (-2)=0,667
Т.е. объем продаж
увеличился на 66,7%
Задача 4
Функция общих затрат имеет вид:
TC=50+6Q+0,5Q2.
Определите:
а) значения FC,
VC, MC, ATC, AFC,
AVC;
б) при каком объеме производства (Q) АТС будет минимальным;
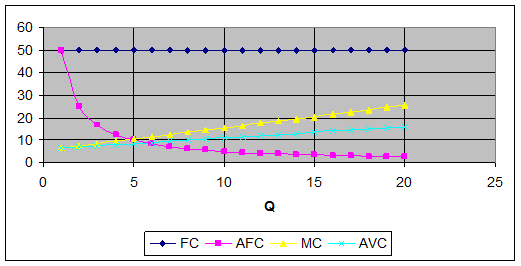
в) постройте графики FC, AFC, MC, AVC;
Решение:
а) Определим значения FC, VC, MC, ATC, AFC, AVC:
TC=50+6Q+0,5Q2
Общие издержки равны сумме постоянных и переменных издержек:
ТС=FC+VC
FC –
постоянные издержки, уровень которых не зависит от Q, значит FC=50, а переменные издержки VC=6Q+0,5Q2
MC –
это предельные издержки, равные дополнительным издержкам на каждую
дополнительную единицу продукции:
MC = VCn+1
- VCn
MC=6(Q+1)+0,5(Q+1)2-6Q-0,5Q2=6,5+Q
ATC,
AFC, AVC – это соответственно средние общие,
постоянные и переменные издержки:
ATC= TC/Q=50/Q+6+0,5Q
AFC=FC/Q=50/Q
AVC= VC/Q=6+0,5Q
б) Подставляя различные значения Q, построим таблицу значений найденных
показателей:
|
Q
|
FC
|
VC
|
MC
|
ATC
|
AFC
|
AVC
|
|
1
|
50
|
6,5
|
-
|
56,5
|
50
|
6,5
|
|
2
|
50
|
14
|
7,5
|
32
|
25
|
7
|
|
3
|
50
|
22,5
|
8,5
|
24,7
|
16,67
|
7,5
|
|
4
|
50
|
32
|
9,5
|
20,5
|
12,5
|
8
|
|
5
|
50
|
42,5
|
10,5
|
18,5
|
10
|
8,5
|
|
6
|
50
|
54
|
11,5
|
17,33
|
8,33
|
9
|
|
7
|
50
|
66,5
|
12,5
|
16,64
|
7,14
|
9,5
|
|
8
|
50
|
80
|
13,5
|
16,25
|
6,25
|
10
|
|
9
|
50
|
94,5
|
14,5
|
16,06
|
5,56
|
10,5
|
|
10
|
50
|
110
|
15,5
|
16,00
|
5,00
|
11
|
|
11
|
50
|
126,5
|
16,5
|
16,05
|
4,55
|
11,5
|
|
12
|
50
|
144
|
17,5
|
16,17
|
4,17
|
12
|
|
13
|
50
|
162,5
|
18,5
|
16,35
|
3,85
|
12,5
|
|
14
|
50
|
182
|
19,5
|
16,57
|
3,57
|
13
|
|
15
|
50
|
202,5
|
20,5
|
16,83
|
3,33
|
13,5
|
|
16
|
50
|
224
|
21,5
|
17,13
|
3,13
|
14
|
|
17
|
50
|
246,5
|
22,5
|
17,44
|
2,94
|
14,5
|
|
18
|
50
|
270
|
23,5
|
17,78
|
2,78
|
15
|
|
19
|
50
|
294,5
|
24,5
|
18,13
|
2,63
|
15,5
|
|
20
|
50
|
320
|
25,5
|
18,5
|
2,5
|
16
|
Как видно из таблицы средние общие издержки ATC будут минимальны при
объеме производства Q=10
ед.
в) Построим графики:
Задача 5
Общие издержки на выпуск товара фирмы заданы в виде:
TC=1000-80Q+2Q2.
Фирма продает товар на рынке чистой конкуренции по цене 120
руб. за ед. Определите максимальный размер прибыли, для фирмы в краткосрочном
периоде.
Решение:
Так как фирма продает товар на рынке чистой конкуренции, то
объем спроса на всем рынке не зависит от объема выпуска данной фирмы, т.е. весь
товар, который выпускает фирма, потребляется в полном объеме.
Функция прибыли имеет вид:
U = TR – TC
= 120Q – (1000-80Q+2Q2) = -1000+200Q-2Q2.
Построим график этой функции:
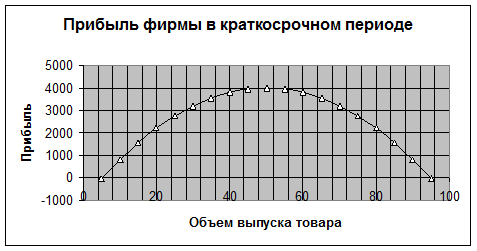
Функция прибыли максимизируется при объеме выпуска товаров Q=50 ед. и эта прибыль равна:
U(Q=50) = -1000 + 200 * 50 – 2
* 502 = 4000
Задача 6
Функция спроса для фирмы-монополиста имеет вид: Qd=50-2P, где: Qd – объем спроса, Р – цена
товара.
Постоянные издержки (FC) равны 120 тыс. руб., а средние переменные (AVC)=4 тыс. руб.
Определите максимальный размер прибыли.
Решение:
Составим таблицу зависимости цены, количества товаров,
валового дохода, валовых издержек и прибыли.
|
Цена, P
|
Количество товаров,
Qd = 50-2P
|
Валовой доход,
P*Qd
|
Средние издержки,
Qd*4
|
Валовые издержки,
Qd*4+120
|
Прибыль,
|
|
0
|
50
|
0
|
200
|
320
|
-320
|
|
1
|
48
|
48
|
192
|
312
|
-264
|
|
2
|
46
|
92
|
184
|
304
|
-212
|
|
3
|
44
|
132
|
176
|
296
|
-164
|
|
4
|
42
|
168
|
168
|
288
|
-120
|
|
5
|
40
|
200
|
160
|
280
|
-80
|
|
6
|
38
|
228
|
152
|
272
|
-44
|
|
7
|
36
|
252
|
144
|
264
|
-12
|
|
8
|
34
|
272
|
136
|
256
|
16
|
|
9
|
32
|
288
|
128
|
248
|
40
|
|
10
|
30
|
300
|
120
|
240
|
60
|
|
11
|
28
|
308
|
112
|
232
|
76
|
|
12
|
26
|
312
|
104
|
224
|
88
|
|
13
|
24
|
312
|
96
|
216
|
96
|
|
14
|
22
|
308
|
88
|
208
|
100
|
|
15
|
20
|
300
|
80
|
200
|
100
|
|
16
|
18
|
288
|
72
|
192
|
96
|
|
17
|
16
|
272
|
64
|
184
|
88
|
|
18
|
14
|
252
|
56
|
176
|
76
|
|
19
|
12
|
228
|
48
|
168
|
60
|
|
20
|
10
|
200
|
40
|
160
|
40
|
|
21
|
8
|
168
|
32
|
152
|
16
|
|
22
|
6
|
132
|
24
|
144
|
-12
|
|
23
|
4
|
92
|
16
|
136
|
-44
|
|
24
|
2
|
48
|
8
|
128
|
-80
|
|
25
|
0
|
0
|
0
|
120
|
-120
|
Прибыль равна валовой доход минус валовые издержки:
U = TR – TC
= P*Qd – (Qd*4+120)
подставив Qd=50-2P, получим функцию прибыли:
U =
-2P2 + 58P - 320
Затем на основе таблицы построим графики этих показателей:
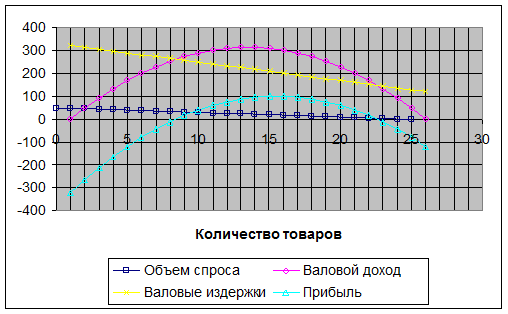
Функция прибыли U = -2P2
+ 58P - 320
максимизируется при цене 14 или 15 руб. В этом случае фирма сможет реализовать
20 или 22 единицы товара и получить максимальную прибыль в 100 тыс. руб.
Задача 7
Пусть функции спроса (Qd) и предложения (Qs) имеют вид: Qd=50-2P,
Qs=4P-10.
При росте доходов покупателей цена товара выросла на 25%, а
правительство ввело налог с продажи в размере 5 руб. за ед. Определите
графически новое состояние равновесия.
Решение:
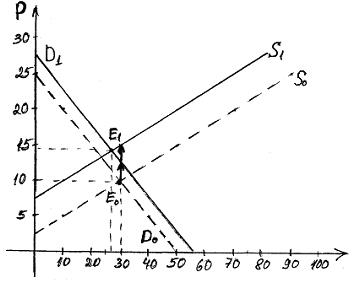
Исходное равновесное состояние предполагает, что на рынке
установилась цена 10 руб., а равновесный объем товаров 30 ед. В результате
роста доходов покупателей и роста цены товара на 25%, кривая спроса сдвинулась
вверх на 2,5 руб (10*25%). А в результате введения налога с продаж в размере 5
руб. за ед., кривая предложения сместилась вверх на 5 руб. Таким образом, на
рынке установилось новое равновесное состояние, показанное на рисунке.
Задача 8
Фирма платит арендную плату за оборудование 800 руб. в день
и заработную плату 200 руб. Предельный продукт, получаемый за счет оборудования
равен 2, а за счет заработной платы 0,5. Эффективно ли фирма использует
ресурсы? Определить цену товара для получения максимальной прибыли.
Решение:
Предельная производительность оборудования равна
2/800=0,0025 на 1 рубль, затраченный на арендную плату. А предельная
производительность труда равна 0,5/200=0,0025 на 1 рубль, затраченный на
заработную плату. Т.е. предельные производительности двух факторов производства
равны, т.е. фирма использует свои ресурсы эффективно.
Т.к. предприятие затрачивает всего в день 200+800=1000 руб.,
а предельный продукт, получаемый за счет этих факторов равен 2,5, то фирма
должна установить цену, превышающую 1000/2,5=400 руб. за единицу изделия.
Список литературы
1.
Баликов В.З. Общая экономическая теория. Учебное
пособие. – М.: «Издательство ПРИОР», Новосибирск: ООО «Издательство ЮКЭА», 1999
2.
Камаева
В.Д. Основы экономической теории. - М.: Изд. МГТУ, 1996.
3. Ивашковский С.Н.
Микроэкономика. – М.: Дело, 2002
4.
Куликов П.М. Основы экономической теории: Учебное
пособие – М.: Финансы и статистика, 2001
5.
Николаев И.П. Экономическая теория – М.: «КноРус», 1998
6.
Носова С.С. Экономическая теория. – М.: Изд-во. «Дашков
и Ко», 2003