ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА СТАТИСТИКИ
О Т Ч Е Т
о
результатах выполнения
компьютерной
лабораторной работы №1
«Автоматизированный
априорный анализ статистической совокупности
в среде MS Excel»
Вариант №_94
Выполнил: ст. III курса гр.вечер
Грачева Ю.А.
Проверил:
_Леонова
С.Н.
Орел, 2008 г.
1. Постановка задачи
При проведении
статистического наблюдения за деятельностью предприятий корпорации получены
выборочные данные по 32-м предприятиям, выпускающим однородную продукцию (выборка 10%-ная, механическая), о среднегодовой
стоимости основных производственных фондов и
о выпуске продукции за год.
В проводимом статистическом
исследовании обследованные предприятия выступают как единицы выборочной
совокупности, а показатели Среднегодовая
стоимость основных производственных фондов и Выпуск продукции – как изучаемые признаки единиц.
Для проведения
автоматизированного статистического анализа совокупности выборочные данные
представлены в формате электронных таблиц процессора Excel в диапазоне ячеек
B4:C35.
Исходные данные
представлены в табл.1.
|
|
Таблица 1
|
|
Исходные данные
|
|
|
Номер предприятия
|
Среднегодовая стоимость основных
производственных фондов, млн.руб.
|
Выпуск продукции, млн. руб.
|
|
1
|
5174,00
|
4944,00
|
|
2
|
6086,00
|
5424,00
|
|
3
|
6278,00
|
6048,00
|
|
4
|
6614,00
|
6720,00
|
|
5
|
4310,00
|
3360,00
|
|
6
|
6950,00
|
5760,00
|
|
7
|
7142,00
|
7776,00
|
|
8
|
5366,00
|
5280,00
|
|
9
|
6566,00
|
6192,00
|
|
10
|
7574,00
|
7728,00
|
|
11
|
2870,00
|
7200,00
|
|
12
|
8294,00
|
8160,00
|
|
13
|
6326,00
|
6432,00
|
|
14
|
6950,00
|
7008,00
|
|
15
|
7958,00
|
8496,00
|
|
16
|
9110,00
|
9120,00
|
|
17
|
6806,00
|
6144,00
|
|
18
|
7526,00
|
7296,00
|
|
19
|
5990,00
|
4560,00
|
|
20
|
7622,00
|
6240,00
|
|
21
|
8486,00
|
8400,00
|
|
22
|
5846,00
|
4752,00
|
|
23
|
4646,00
|
4464,00
|
|
24
|
7766,00
|
7152,00
|
|
25
|
6950,00
|
6240,00
|
|
26
|
6470,00
|
5904,00
|
|
27
|
5030,00
|
3840,00
|
|
28
|
6758,00
|
6000,00
|
|
29
|
7814,00
|
6576,00
|
|
30
|
9110,00
|
2400,00
|
|
31
|
7430,00
|
6240,00
|
|
32
|
5462,00
|
5568,00
|
В процессе исследования совокупности
необходимо решить ряд задач.
I. Статистический анализ выборочной совокупности
1. Выявить наличие среди
исходных данных резко выделяющихся значений признаков («выбросов» данных) с
целью исключения из выборки аномальных единиц наблюдения.
2. Рассчитать обобщающие
статистические показатели совокупности по изучаемым признакам: среднюю
арифметическую (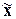 ), моду (Мо), медиану
(Ме), размах вариации (R), дисперсию(
), моду (Мо), медиану
(Ме), размах вариации (R), дисперсию(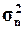 ), средние отклонения – линейное (
), средние отклонения – линейное (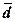 ) и квадратическое (σn),
коэффициент вариации (Vσ),
структурный коэффициент асимметрии
К.Пирсона (Asп).
) и квадратическое (σn),
коэффициент вариации (Vσ),
структурный коэффициент асимметрии
К.Пирсона (Asп).
3. На основе рассчитанных
показателей в предположении, что распределения единиц по обоим признакам близки
к нормальному, оценить:
а) степень колеблемости
значений признаков в совокупности;
б) степень однородности
совокупности по изучаемым признакам;
в) устойчивость
индивидуальных значений признаков;
г) количество попаданий индивидуальных
значений признаков в диапазоны (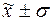 ), (
), (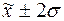 ), (
), (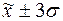 ).
).
4. Дать сравнительную
характеристику распределений единиц совокупности по двум изучаемым признакам на
основе анализа:
а) вариации признаков;
б) количественной
однородности единиц;
в) надежности (типичности)
средних значений признаков;
г) симметричности распределений в центральной части ряда.
5. Построить интервальный
вариационный ряд и гистограмму распределения единиц совокупности по признаку Среднегодовая стоимость основных
производственных фондов и установить характер (тип) этого распределения.
6. Сделать заключение о
возможности практического использования в качестве адекватной модели
взаимосвязи изучаемых признаков линейной модели, полученной с помощью
инструмента Регрессия.
II. Статистический анализ генеральной совокупности
1. Рассчитать генеральную
дисперсию 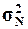 , генеральное среднее
квадратическое отклонение
, генеральное среднее
квадратическое отклонение 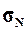 и ожидаемый размах вариации признаков RN. Сопоставить значения этих
показателей для генеральной и выборочной дисперсий.
и ожидаемый размах вариации признаков RN. Сопоставить значения этих
показателей для генеральной и выборочной дисперсий.
2. Для изучаемых признаков
рассчитать:
а) среднюю ошибку выборки;
б) предельные ошибки выборки
для уровней надежности P=0,683, P=0,954, P=0,997 и границы, в которых будут
находиться средние значения признака генеральной совокупности при заданных
уровнях надежности.
3. Рассчитать коэффициенты
асимметрии As и эксцесса Ek. На основе полученных оценок сделать вывод об особенностях формы
распределения единиц генеральной совокупности.
III.
Экономическая интерпретация результатов статистического исследования
предприятий
В этой части исследования необходимо ответить на ряд
вопросов.
1. Типичны ли образующие
выборку предприятия по значениям изучаемых экономических показателей?
2. Каковы наиболее характерные
для предприятий значения показателей среднегодовой стоимости основных фондов и
выпуска продукции?
3. Насколько сильны различия в
экономических характеристиках предприятий выборочной совокупности? Можно ли
утверждать, что выборка сформирована из предприятий с достаточно близкими
значениями по каждому из показателей?
4. Какова структура предприятий
выборочной совокупности по среднегодовой стоимости основных фондов? Каков
удельный вес предприятий с наибольшими, наименьшими и типичными значениями
данного показатели? Какие именно это предприятия?
5. Носит ли распределение
предприятий по группам закономерный характер и какие предприятия (с более
высокой или более низкой стоимостью основных фондов) преобладают в
совокупности?
6. Каковы ожидаемые средние
величины среднегодовой стоимости основных фондов и выпуска продукции на
предприятиях корпорации в целом? Какое максимальное расхождение в значениях
показателя можно ожидать?
2. Рабочий файл с результативными таблицами и графиками
См. Приложение 1
3. Выводы по результатам выполнения лабораторной работы
I. Статистический анализ выборочной совокупности
Задача 1. В результате визуального
анализа диаграммы рассеивания признаков единиц наблюдаемой совокупности выявлены
следующие аномальные единицы наблюдения:
|
|
Таблица 2
|
|
Аномальные единицы
наблюдения
|
|
Номер предприятия
|
Среднегодовая стоимость основных
производственных фондов, млн.руб.
|
Выпуск продукции, млн. руб.
|
|
11
|
2870,00
|
7200,00
|
|
30
|
9110,00
|
2400,00
|
Приведенные в таблице 2
аномальные единицы наблюдения удалены из изучаемой совокупности.
Корреляционное поле имеет
вид:
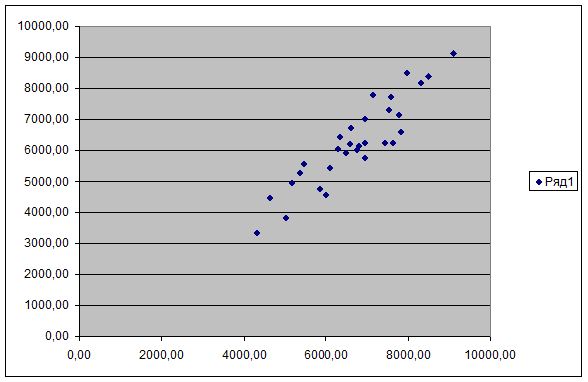
После исключения аномальных
наблюдений первичные данные имеют вид, представленный в таблице 1.
|
|
Таблица 1
|
|
Исходные данные
|
|
|
Номер предприятия
|
Среднегодовая стоимость основных
производственных фондов, млн.руб.
|
Выпуск продукции, млн. руб.
|
|
1
|
5174,00
|
4944,00
|
|
2
|
6086,00
|
5424,00
|
|
3
|
6278,00
|
6048,00
|
|
4
|
6614,00
|
6720,00
|
|
5
|
4310,00
|
3360,00
|
|
6
|
6950,00
|
5760,00
|
|
7
|
7142,00
|
7776,00
|
|
8
|
5366,00
|
5280,00
|
|
9
|
6566,00
|
6192,00
|
|
10
|
7574,00
|
7728,00
|
|
12
|
8294,00
|
8160,00
|
|
13
|
6326,00
|
6432,00
|
|
14
|
6950,00
|
7008,00
|
|
15
|
7958,00
|
8496,00
|
|
16
|
9110,00
|
9120,00
|
|
17
|
6806,00
|
6144,00
|
|
18
|
7526,00
|
7296,00
|
|
19
|
5990,00
|
4560,00
|
|
20
|
7622,00
|
6240,00
|
|
21
|
8486,00
|
8400,00
|
|
22
|
5846,00
|
4752,00
|
|
23
|
4646,00
|
4464,00
|
|
24
|
7766,00
|
7152,00
|
|
25
|
6950,00
|
6240,00
|
|
26
|
6470,00
|
5904,00
|
|
27
|
5030,00
|
3840,00
|
|
28
|
6758,00
|
6000,00
|
|
29
|
7814,00
|
6576,00
|
|
31
|
7430,00
|
6240,00
|
|
32
|
5462,00
|
5568,00
|
Задача 2. Расчеты параметров, определяемых инструментом Описательная статистика
приведены в таблице 3
|
|
|
Таблица 3
|
|
Описательные
статистики
|
|
По столбцу "Среднегодовая
стоимость основных производственных фондов, млн.руб."
|
По столбцу "Выпуск
продукции, млн.руб"
|
|
Столбец1
|
|
Столбец2
|
|
|
|
|
|
|
Среднее
|
6710
|
Среднее
|
6260,8
|
|
Стандартная
ошибка
|
211,97
|
Стандартная
ошибка
|
252,86
|
|
Медиана
|
6782
|
Медиана
|
6216
|
|
Мода
|
6950
|
Мода
|
6240
|
|
Стандартное
отклонение
|
1160,999332
|
Стандартное
отклонение
|
1384,972511
|
|
Дисперсия
выборки
|
1347919,448
|
Дисперсия
выборки
|
1918148,855
|
|
Эксцесс
|
-0,344943844
|
Эксцесс
|
-0,205332365
|
|
Асимметричность
|
-0,152503649
|
Асимметричность
|
0,042954448
|
|
Интервал
|
4800
|
Интервал
|
5760
|
|
Минимум
|
4310
|
Минимум
|
3360
|
|
Максимум
|
9110
|
Максимум
|
9120
|
|
Сумма
|
201300
|
Сумма
|
187824
|
|
Счет
|
30
|
Счет
|
30
|
|
Уровень
надежности(95,4%)
|
441,9142862
|
Уровень
надежности(95,4%)
|
527,1657973
|
|
|
|
Таблица 5
|
|
Выборочные показатели вариации и асимметрии
|
|
|
По столбцу "Среднегодовая
стоимость основных производственных фондов, млн.руб."
|
По столбцу "Выпуск продукции,
млн.руб"
|
|
Стандартное
отклонение
|
1141,485348
|
Стандартное
отклонение
|
1361,694004
|
|
Дисперсия
|
1302988,8
|
Дисперсия
|
1854210,56
|
|
Среднее
линейное отклонение
|
918,4
|
Среднее
линейное отклонение
|
1048,96
|
|
Коэффициент
вариации, %
|
17,01170415
|
Коэффициент
вариации, %
|
21,74952089
|
|
Коэффициент
асимметрии Asп
|
-0,21025237
|
Коэффициент
асимметрии Asп
|
0,015275091
|
Таблица 8
Описательные статистики
выборочной совокупности
|
Обобщающие статистические
показатели совокупности по изучаемым признакам
|
Признаки
|
|
Среднегодовая стоимость основных производственных фондов
|
Выпуск продукции
|
|
Средняя
арифметическая (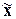 ) )
|
6710
|
6260,8
|
|
Мода
(Мо)
|
6950
|
6240
|
|
Медиана
(Ме)
|
6782
|
6216
|
|
Размах
вариации(R)
|
4800
|
5760
|
|
Дисперсия(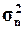 ) )
|
1302988,8
|
1854210,56
|
|
Среднее
линейное отклонение (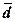 ) )
|
918,4
|
1048,96
|
|
Среднее
квадратическое отклонение (σn)
|
1141,49
|
1361,69
|
|
Коэффициент
вариации (Vσ)
|
17,01
|
21,75
|
|
Коэффициент
асимметрии К.Пирсона (Asп)
|
-0,21
|
0,015
|
Задача 3.
3а). Степень колеблемости признака определяется
по значению коэффициента вариации Vs в соответствии с оценочной
шкалой колеблемости признака.
Для признака Среднегодовая стоимость основных
производственных фондов показатель Vs =17,01
Для признака Выпуск продукции показатель Vs =21,75
Вывод: После удаления аномальных
значений коэффициент вариации Vs признака Среднегодовая стоимость основных
производственных фондов составляет
17,01 %, что свидетельствует о ее незначительной степени колеблемости признака.
Коэффициент вариации признака Выпуск
продукции составляет 21,75 %, что свидетельствует так же о его
незначительной колеблемости признака.
3б). Однородная совокупность.
Для признака Среднегодовая стоимость основных
производственных фондов показатель Vs =17,01
Для признака Выпуск продукции показатель Vs =21,75
Вывод: Однородность совокупности для нормального и близких к
нормальному распределений устанавливается по условию V≤33%.
Коэффициент вариации
признака Среднегодовая стоимость основных производственных фондов составляет Vs =17,01%, что свидетельствует об однородности
изучаемой совокупности.
Коэффициент вариации признака
Выпуск продукции составляет Vs =21,75 что свидетельствует об однородности изучаемой
совокупности. Чем однороднее изучаемая совокупность, тем надежнее полученная
средняя.
3в). Сопоставление средних
отклонений – квадратического s и линейного 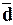 позволяет сделать
вывод об устойчивости индивидуальных значений признака, т.е. об
отсутствии среди них «аномальных» вариантов значений.
позволяет сделать
вывод об устойчивости индивидуальных значений признака, т.е. об
отсутствии среди них «аномальных» вариантов значений.
В условиях симметричного и
нормального, а также близких к ним распределений между показателями s и 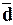 имеют место равенства s
имеют место равенства s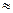 1,25
1,25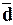 ,
, 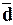
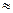 0,8s, поэтому отношение
показателей
0,8s, поэтому отношение
показателей 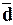 и s может
служить индикатором устойчивости данных.
и s может
служить индикатором устойчивости данных.
Если 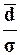 >0,8, то
значения признака неустойчивы, в них имеются «аномальные» выбросы.
Следовательно, несмотря на визуальное обнаружение и исключение нетипичных
единиц наблюдений при выполнении Задания 1, некоторые аномалии в первичных
данных продолжают сохраняться. В этом случае их следует выявить (например,
путем поиска значений, выходящих за границы (
>0,8, то
значения признака неустойчивы, в них имеются «аномальные» выбросы.
Следовательно, несмотря на визуальное обнаружение и исключение нетипичных
единиц наблюдений при выполнении Задания 1, некоторые аномалии в первичных
данных продолжают сохраняться. В этом случае их следует выявить (например,
путем поиска значений, выходящих за границы (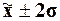 )) и рассматривать
в качестве возможных «кандидатов» на исключение из выборки.
)) и рассматривать
в качестве возможных «кандидатов» на исключение из выборки.
Для признака Среднегодовая стоимость основных
производственных фондов показатель 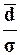 =
=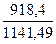 =0,79
=0,79
Для признака Выпуск продукции показатель 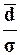 =
=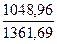 =0,77
=0,77
Вывод: Отношение показателей s и 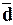 может служить
индикатором устойчивости данных:
может служить
индикатором устойчивости данных: 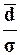 <0,8,
то можно сделать вывод об устойчивости индивидуальных значений признака, среди
них отсутствуют «аномальные» выбросы.
<0,8,
то можно сделать вывод об устойчивости индивидуальных значений признака, среди
них отсутствуют «аномальные» выбросы.
3г). Для оценки количества
попаданий индивидуальных значений признаков xi в тот или иной диапазон отклонения от средней 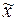 , а также для установления процентного соотношения рассеяния
значений xi по 3-м диапазонам
формируется табл.9 (с конкретными числовыми значениями границ диапазонов).
, а также для установления процентного соотношения рассеяния
значений xi по 3-м диапазонам
формируется табл.9 (с конкретными числовыми значениями границ диапазонов).
Таблица 9
Распределение
значений признака по диапазонам рассеяния признака относительно 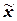
|
Границы диапазонов
|
Количество значений
xi,
находящихся в диапазоне
|
Процентное
соотношение рассеяния значений xi по диапазонам, %
|
|
Первый признак
|
Второй признак
|
Первый признак
|
Второй признак
|
Первый признак
|
Второй признак
|
|
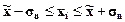
|
[
5549 ;7871]
|
[4876
; 7646]
|
20
|
21
|
211,97
|
252,86
|
|
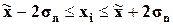
|
[
4388 ; 9032 ]
|
[3491
; 9031]
|
28
|
29
|
423,94
|
505,72
|
|
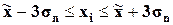
|
[
3227; 10193]
|
[2106
; 10416]
|
31
|
32
|
635,91
|
758,58
|
На основе данных табл.9 процентное соотношение
рассеяния значений признака по трем диапазонам сопоставляется с рассеянием по
правилу «трех сигм», справедливому для нормальных и близких к нему
распределений:
68,3% значений располагаются в диапазоне (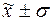 ),
),
95,4% значений располагаются в диапазоне (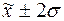 ),
),
99,7% значений располагаются в диапазоне (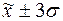 ).
).
Для признака среднегодовая
стоимость основных фондов:
68,3% значений располагаются в диапазоне от 5549 до
7871,
95,4% значений располагаются в диапазоне от4388 до
9032,
99,7% значений располагаются в диапазоне от 3227 до
10193.
Для признака выпуска
продукции:
68,3% значений располагаются в диапазоне от
4876 до 7646 ,
95,4% значений располагаются в диапазоне от 3491 до
9031,
99,7% значений располагаются в диапазоне от
2106 до10416.
Ожидаемые границы вариации выборки для признака
«Среднегодовая стоимость основных производственных фондов» соответствуют:
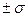 с вероятностью
Р=68,3%, т.е
с вероятностью
Р=68,3%, т.е 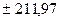
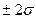 вероятностью Р=95,4%,
т.е
вероятностью Р=95,4%,
т.е 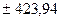
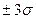 вероятностью Р=99,7%,
т.е
вероятностью Р=99,7%,
т.е 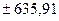
Ожидаемые границы вариации выборки для признака «Выпуск
продукции» соответствуют:
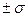 с вероятностью
Р=68,3%, т.е
с вероятностью
Р=68,3%, т.е 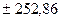
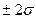 вероятностью Р=95,4%,
т.е
вероятностью Р=95,4%,
т.е 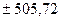
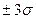 вероятностью Р=99,7%,
т.е
вероятностью Р=99,7%,
т.е 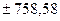
Вывод: процентное соотношение
рассеяния хi по 3-м диапазонам незначительно расходится с
правилом «3-х сигм», можно предположить, что изучаемое распределение признака
близко к нормальному.
Задача 4. Для ответа на вопросы 4а) – 4г) необходимо воспользоваться табл.8 и сравнить
величины показателей для двух признаков.
4а). Для сравнения колеблемости значений признаков, имеющих разные средние 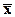 , используется коэффициент вариации Vs.
, используется коэффициент вариации Vs.
Вывод: Так как Vs для первого
признака меньше (17,01), чем Vs для второго признака (21,75), то колеблемость значений
первого признака меньше колеблемости значений второго признака.
4б). Сравнение
количественной однородности единиц.
Чем меньше значение
коэффициента вариации Vs, тем
более однородна совокупность.
Вывод: Так как значение Vs для обоих признаков невелико, т.е Vs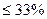 , следовательно, средняя арифметическая величина является
надежной характеристикой данной совокупности.
, следовательно, средняя арифметическая величина является
надежной характеристикой данной совокупности.
4в). Сравнение надежности (типичности) средних значений
признаков.
Чем более однородна
совокупность, тем надежнее среднее значение признака 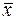
4г). Сравнение симметричности распределений в центральной части ряда.
В нормальных и близких к
нему распределениях основная масса единиц (63,8%) располагается в центральной
части ряда, в диапазоне (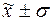 ). Для оценки асимметрии распределения в этом центральном
диапазоне служит коэффициент К.Пирсона – Asп.
). Для оценки асимметрии распределения в этом центральном
диапазоне служит коэффициент К.Пирсона – Asп.
При правосторонней асимметрии
Asп>0, при левосторонней – Asп<0. Если Asп=0,
вариационный ряд симметричен.
Вывод: в)-г) По таблице 8 видно, что Asп<0 (Asп
= -0,21) для признака «Среднегодовая стоимость
основных производственных фондов», и это означает, что асимметрия левосторонняя,
для которой справедливо неравенство 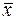 <Me<Mo, что в распределении чаще
встречаются более низкие значения признака, а для признака «Выпуск продукции» Asп>0, т.е. Asп=0,02, и это означает, что
асимметрия правосторонняя, для которой справедливо неравенство
<Me<Mo, что в распределении чаще
встречаются более низкие значения признака, а для признака «Выпуск продукции» Asп>0, т.е. Asп=0,02, и это означает, что
асимметрия правосторонняя, для которой справедливо неравенство 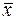 >Me >Mo,
означающее, что в распоряжении чаще встречаются более высокие значения
признака.
>Me >Mo,
означающее, что в распоряжении чаще встречаются более высокие значения
признака.
Задача 5. Интервальный вариационный ряд распределения единиц совокупности по
признаку Среднегодовая стоимость основных
производственных фондов представлен в табл.7.1, а гистограмма и кумулята –
на рис.2.
|
|
Таблица 7,1
|
|
Интервальный ряд
распределения предприятий
по стоимости основных производственных
фондов
|
|
группы предприятий по стоимости
основных фондов
|
число предприятий в группе
|
накопленная часть группы
|
|
4310-5270
|
4
|
13,33%
|
|
5270-6230
|
5
|
30,00%
|
|
6230-7190
|
11
|
66,67%
|
|
7190-8150
|
7
|
90,00%
|
|
8150-9110
|
3
|
100,00%
|
|
итого
|
30
|
|
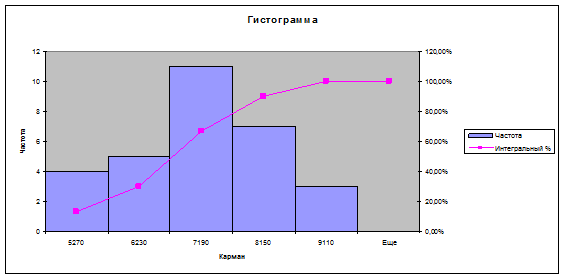
Рис.2
Возможность отнесения
распределения признака «Среднегодовая
стоимость основных производственных фондов» к семейству нормальных
распределений устанавливается путем анализа формы гистограммы распределения.
Анализируется количество вершин в гистограмме, ее асимметричность и
выраженность «хвостов», т.е. частоты появления в распределении значений,
выходящих за диапазон (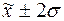 ).
).
1. При анализе формы
гистограммы прежде всего следует оценить распределение вариантов признака по
интервалам (группам). Если на гистограмме четко прослеживаются два-три «горба»
частот вариантов, это говорит о том, что значения признака концентрируются
сразу в нескольких интервалах, что не соответствует нормальному закону
распределения.
Заключение по п.1: гистограмма имеет одновершинную форму, есть основания
предполагать, что выборочная совокупность может иметь характер распределения,
близкий к нормальному.
2. Для дальнейшего
анализа формы распределения используются
описательные параметры выборки - показатели центра распределения (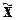 , Mo, Me), вариации (
, Mo, Me), вариации (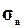 ),
асимметрии в центральной части
распределения (AsП). Совокупность этих показателей позволяет дать качественную оценку
близости эмпирических данных к нормальной форме распределения.
),
асимметрии в центральной части
распределения (AsП). Совокупность этих показателей позволяет дать качественную оценку
близости эмпирических данных к нормальной форме распределения.
Нормальное
распределение является симметричным, и для него выполняется соотношения:
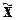 =Mo=Me, Asп=0,
Rn=6sn.
=Mo=Me, Asп=0,
Rn=6sn.
Нарушение этих соотношений свидетельствует о наличии
асимметрии распределения. Распределение с небольшой или умеренной асимметрией в
большинстве случаев относятся к нормальному типу.
Заключение по
п.2: Asп<0 (Asп
= -0,21) для признака «Среднегодовая стоимость
основных производственных фондов», и это означает, что асимметрия
левосторонняя, 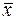 <Me<Mo, это говорит о том, что в
распределении чаще встречаются более низкие значения признака, а для признака
«Выпуск продукции» Asп>0,
т.е. Asп=0,02, и это
означает, что асимметрия правосторонняя,
<Me<Mo, это говорит о том, что в
распределении чаще встречаются более низкие значения признака, а для признака
«Выпуск продукции» Asп>0,
т.е. Asп=0,02, и это
означает, что асимметрия правосторонняя, 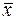 >Me >Mo и это
означает, что в распоряжении чаще встречаются более высокие значения признака.
>Me >Mo и это
означает, что в распоряжении чаще встречаются более высокие значения признака.
3. В нормальном и близким к
нему распределениях крайние варианты значения признака (близкие к хmin и хmax) встречаются много реже (5-7 % всех
случаев), чем серединные (лежащие в диапазоне (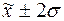 )).
Следовательно, по проценту выхода значений признака за пределы диапазона (
)).
Следовательно, по проценту выхода значений признака за пределы диапазона (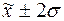 )
можно судить о соответствии длины «хвостов» распределения нормальному закону.
)
можно судить о соответствии длины «хвостов» распределения нормальному закону.
Заключение по
п.3: т.к. крайние варианты обоих признаков
встречаются не так часто (10%), чем серединные, значит длина «хвостов» не
совсем соответствует нормальному закону распределения
Вывод: Гистограмма является одновершинной, приблизительно
симметричной,“хвосты” распределения немного длинны, т.к. 10% вариантов лежат за
пределами интервала (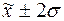 ),
следовательно, вполне можно судить о
соответствии распределения нормальному закону.
),
следовательно, вполне можно судить о
соответствии распределения нормальному закону.
II.
Статистический анализ генеральной
совокупности
Задача 1. Рассчитанные генеральные
показатели представлены в табл.10.
Таблица 10
Описательные статистики
генеральной совокупности
|
Обобщающие статистические
показатели совокупности по изучаемым признакам
|
Признаки
|
|
Среднегодовая стоимость основных производственных фондов
|
Выпуск продукции
|
|
Стандартное
отклонение 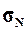
|
1160,99
|
1384,97
|
|
Дисперсия
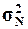
|
1347919,3
|
1918148,6
|
|
Асимметричность
As
|
-0,015
|
0,043
|
|
Эксцесс
Ek
|
-0,34
|
-0,21
|
|
Ожидаемый
размах вариации признаков RN
|
6848,94
|
8170,14
|
Величина дисперсии
генеральной совокупности 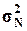 может быть оценена
непосредственно по выборочной дисперсии
может быть оценена
непосредственно по выборочной дисперсии 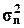 .
.
В математической статистике
доказано, что при малом числе наблюдений (особенно при n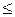 40-50) для
вычисления генеральной дисперсии
40-50) для
вычисления генеральной дисперсии 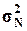 по выборочной
дисперсии
по выборочной
дисперсии 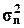 следует использовать
формулу
следует использовать
формулу
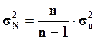 .
.
При достаточно больших n значение поправочного коэффициента 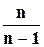 близко к единице (при
n=100 его значение равно 1,101, а
при n=500 - 1,002 и т.д.). Поэтому
при достаточно больших n можно
приближено считать, что обе дисперсии совпадают:
близко к единице (при
n=100 его значение равно 1,101, а
при n=500 - 1,002 и т.д.). Поэтому
при достаточно больших n можно
приближено считать, что обе дисперсии совпадают:
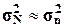 .
.
Рассчитаем отношение 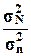 для двух признаков:
для двух признаков:
Для первого
признака 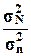 =
=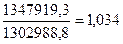 , для второго признака
, для второго признака 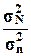 =
=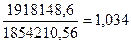
Вывод:
Степень расхождения между признаками оценивается величиной 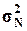 и
и 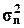 , которая равна 1,034, и эти расхождения незначительны, или
даже можно сказать точнее приблизительно равны (отличаются на несколько тысяч
сотых).
, которая равна 1,034, и эти расхождения незначительны, или
даже можно сказать точнее приблизительно равны (отличаются на несколько тысяч
сотых).
Для нормального
распределения справедливо равенство RN=6sN.
В условиях
близости распределения единиц генеральной совокупности к нормальному это
соотношение используется для прогнозной оценки размаха вариации признака в
генеральной совокупности.
Ожидаемый размах вариации
признаков RN:
- для первого
признака RN =6*1141,49=6848,94,
- для второго
признака RN
=6*1361,69=8170,14.
Величина расхождения
между показателями RN и Rn:
- для первого
признака |RN -Rn|=6848,94-4800=2048,94
- для второго
признака |RN -Rn| =8170,14-5760=2410,14
Задача 2. Применение выборочного метода наблюдения связано
с измерением степени достоверности статистических характеристик генеральной
совокупности, полученных по результатам выборочного наблюдения. Достоверность
генеральных параметров зависит от репрезентативности выборки, т.е. от
того, насколько полно и адекватно представлены в выборке статистические
свойства генеральной совокупности.
Как правило,
статистические характеристики выборочной и генеральной совокупностей не
совпадают, а отклоняются на некоторую величину ε, которую называют ошибкой выборки (ошибкой репрезентативности).
Ошибка выборки – это разность между значением показателя, который был получен
по выборке, и генеральным значением этого показателя. Например, разность
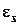 = |
= |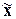 -
-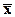 |
|
определяет ошибку
репрезентативности для средней величины признака.
Для среднего
значения признака средняя ошибка выборки 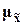 (ее называют
также стандартной ошибкой) выражает среднее квадратическое отклонение s выборочной
средней
(ее называют
также стандартной ошибкой) выражает среднее квадратическое отклонение s выборочной
средней 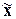 от математического
ожидания M[
от математического
ожидания M[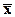 ] генеральной средней
] генеральной средней 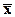 .
.
Для
изучаемых признаков средние ошибки выборки 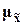 даны в табл.
3:
даны в табл.
3:
- для
признака Среднегодовая стоимость основных
производственных фондов
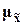 =211,96850774551,
=211,96850774551,
- для признака Выпуск продукции
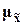 =252,86022853
=252,86022853
Предельная ошибка выборки 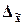 определяет границы, в пределах которых лежит генеральная средняя
определяет границы, в пределах которых лежит генеральная средняя 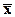 . Эти границы задают так называемый доверительный интервал
генеральной средней
. Эти границы задают так называемый доверительный интервал
генеральной средней 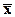 – случайную
область значений, которая с вероятностью P,
близкой к 1, гарантированно содержит значение
генеральной средней. Эту вероятность называют доверительной вероятностью или
уровнем
надежности.
– случайную
область значений, которая с вероятностью P,
близкой к 1, гарантированно содержит значение
генеральной средней. Эту вероятность называют доверительной вероятностью или
уровнем
надежности.
Для уровней надежности P=0,954; P=0,997; P=0,683 оценки
предельных ошибок выборки 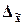 даны в табл. 3, табл. 4а и табл. 4б.
даны в табл. 3, табл. 4а и табл. 4б.
Для генеральной средней
предельные значения и доверительные интервалы определяются выражениями:
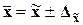 ,
,
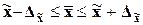
Предельные ошибки выборки и
ожидаемые границы для генеральных средних представлены в табл. 11.
Таблица
11
Предельные ошибки выборки и
ожидаемые границы для генеральных средних
|
Доверительная
вероятность
Р
|
Коэффициент
доверия
t
|
Предельные ошибки
выборки
|
Ожидаемые границы
для средних 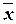
|
|
для первого
признака
|
для второго
признака
|
для первого
признака
|
для второго
признака
|
|
0,683
|
1
|
215,827561461
|
257,4637482
|
6494,17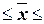 6925,83 6925,83
|
6003,34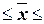 6518,26 6518,26
|
|
0,954
|
2
|
441,91428618
|
527,16579733
|
6268,09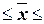 7151,91 7151,91
|
5733,63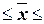 6787,97 6787,97
|
|
0,997
|
3
|
686,652918588
|
819,11797069
|
6023,35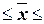 7396,65 7396,65
|
5441,68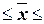 7079,92 7079,92
|
Задача 3 Значения коэффициентов
асимметрии As и эксцесса Ek даны в табл.10.
Показатель асимметрии As оценивает смещение ряда распределения влево или
вправо по отношению к оси симметрии нормального распределения.
Если
асимметрия правосторонняя (As>0)
то правая
часть эмпирической кривой оказывается длиннее левой, т.е. имеет место
неравенство 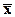 >Me>Mo, что
означает преимущественное появление в распределении более высоких значений
признака. (среднее значение
>Me>Mo, что
означает преимущественное появление в распределении более высоких значений
признака. (среднее значение 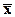 больше серединного
Me и модального Mo).
больше серединного
Me и модального Mo).
Если асимметрия
левосторонняя (As<0), то левая
часть эмпирической кривой оказывается длиннее правой и выполняется
неравенство 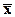 <Me<Mo, означающее,
что в распределении чаще встречаются более низкие значения признака (среднее
значение
<Me<Mo, означающее,
что в распределении чаще встречаются более низкие значения признака (среднее
значение 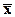 меньше серединного
Me и модального Mo).
меньше серединного
Me и модального Mo).
Чем больше величина |As|, тем более асимметрично распределение. Оценочная шкала
асимметрии:
|As|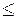 0,25 - асимметрия незначительная;
0,25 - асимметрия незначительная;
0,25<|As|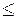 0.5 - асимметрия
заметная (умеренная);
0.5 - асимметрия
заметная (умеренная);
|As|>0,5 - асимметрия существенная.
Вывод: Для признака Среднегодовая стоимость основных
производственных фондов наблюдается незначительная левосторонняя асимметрия,
для признака Выпуск продукции
асимметрия умеренная.
Показатель эксцесса Ek характеризует крутизну
кривой распределения - ее заостренность или пологость по сравнению с нормальной
кривой.
Как правило, коэффициент
эксцесса вычисляется только для симметричных или близких к ним распределений.
Если Ek>0, то вершина кривой распределения располагается выше вершины нормальной кривой, а форма кривой
является более островершинной, чем нормальная. Это говорит о скоплении значений
признака в центральной зоне ряда распределения, т.е. о преимущественном появлении в
данных значений, близких к средней величине.
Если Ek<0, то вершина кривой распределения лежит ниже вершины нормальной
кривой, а форма кривой более пологая по сравнению с нормальной. Это означает,
что значения признака не концентрируются в центральной части ряда, а достаточно
равномерно рассеяны по всему диапазону от xmax до xmin.
Для нормального
распределения Ek=0. При
незначительном отклонении Ek от нуля
форма кривой эмпирического распределения незначительно отличается от формы
нормального распределения. Чем больше абсолютная величина |Ek|,
тем существеннее распределение отличается от нормального.
Вывод:Для
обоих признаков Ek<0, вершина кривой распределения лежит ниже
вершины нормальной кривой, а форма кривой более пологая по сравнению с
нормальной. Значения признака не концентрируются в центральной части ряда, а
достаточно равномерно рассеяны по всему диапазону от xmax до xmin.
III.
Экономическая интерпретация результатов статистического исследования
предприятий
Задача 1.
Вывод: изученные показатели фирмы позволяют построить
одновершинную кривую нормального распределения, это означает, что они типичны
между собой, однако, предприятия №11 и №30 исключены из проводимого исследования,
т.к. являются не типичными в изучаемой совокупности.
Задача 2.
Вывод: средние показатели предприятий: среднегодовая
стоимость основных производственных фондов равняется 6710 млн.руб.; выпуск продукции
составляет в среднем 6260,8 млн.руб. по средней годовой стоимости основных
производственных фондов в диапазон [5549; 7871] входят 20 предприятий, а в по
величине выпуска продукции в диапазон [4876; 7646] 21 предприятий.
Задача 3.
Вывод: различия предприятий выборочной совокупности в
экономических характеристиках не сильны, т.к. коэффициенты вариации по каждому
из двух признаков не превышают 33%, но совокупность первого признака является
более однородной т.к. коэффициент вариации
первого признака меньше второго на 4,63 и составляет 17,01. Расхождение
показателей по первому признаку составляет 4800 млн.руб. по второму 5760
млн.руб.
Задача 4.
Вывод: структура предприятий выборочной совокупности по
среднегодовой стоимости основных производственных фондов состоит из 5 групп.
Удельный вес предприятий с типичными значениями составил 66,67 %, что составило
11 предприятий, с наибольшими значениями 100%, что составило 3 предприятия и с
наименьшими значениями 13,33% - 4
предприятия, 30%-5 предприятий, 90%- 7 предприятий.
Задача 5.
Вывод: в общей совокупности преобладают предприятия с почти
самой высокой стоимостью основных производственных фондов.
Задача 6.
Вывод: ожидаемый размах
вариации по среднегодовой стоимости основных производственных фондов составит
384,18 млн.руб. , а для второго признака 451,92 соответственно
ВСЕРОССИЙСКИЙ
ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА
СТАТИСТИКИ
О
Т Ч Е Т
о результатах выполнения
компьютерной лабораторной работы №2
Автоматизированный корреляционно-регрессионный анализ взаимосвязи статистических
данных в среде MS Excel
Вариант №_94
Выполнил:
ст. III курса грГрачева
Ю.А.
ПроверилЛеонова
С.Н.
.
Орел,
2006 г.
1.
Постановка задачи
Корреляционно-регрессионный анализ взаимосвязи
признаков является составной частью проводимого статистического исследования и
частично использует результаты Лабораторной работы № 1.
В Лабораторной работе № 2 изучается взаимосвязь между
факторным признаком Среднегодовая стоимость
основных производственных фондов (признак Х)
и результативным признаком Выпуск
продукции (признак Y), значениями которых
являются исходные данные Лабораторной работы № 1 после исключения из них
аномальных значений.
См.Приложение 2
В процессе статистического исследования
необходимо решить ряд задач.
1. Установить наличие стохастической
связи между факторным признаком Х
и результативным признаком Y:
а) графическим методом;
б) методом сопоставления параллельных рядов.
2. Установить наличие корреляционной
связи между признаками Х и Y методом аналитической группировки.
3. Оценить тесноту связи признаков Х и
Y на основе:
а) эмпирического корреляционного отношения η;
б) линейного коэффициента корреляции r.
Сравнить значения η и r и сделать вывод о возможности линейной связи между признаками Х
и Y.
4. Построить однофакторную
линейную регрессионную модель связи признаков Х и Y, используя
инструмент Регрессия надстройки Пакет анализа, и рассчитать
доверительные интервалы коэффициентов уравнения линейной регрессии.
Построить теоретическую линию регрессии.
Дать экономическую интерпретацию коэффициента
регрессии.
Рассчитать
коэффициент эластичности и дать его экономическую интерпретацию.
5. Найти наиболее адекватное
нелинейное уравнение регрессии с помощью средств инструмента Мастер диаграмм. Построить для этого
уравнения теоретическую кривую регрессии.
II. Рабочий файл с результативными таблицами и
графиками.
|
|
Таблица 2.1
|
|
Исходные данные
|
|
Номер предприятия
|
Среднегодовая стоимость основных
производственных фондов, млн.руб.
|
Выпуск продукции, млн. руб.
|
|
5
|
4310,00
|
3360,00
|
|
23
|
4646,00
|
4464,00
|
|
27
|
5030,00
|
3840,00
|
|
1
|
5174,00
|
4944,00
|
|
8
|
5366,00
|
5280,00
|
|
32
|
5462,00
|
5568,00
|
|
22
|
5846,00
|
4752,00
|
|
19
|
5990,00
|
4560,00
|
|
2
|
6086,00
|
5424,00
|
|
3
|
6278,00
|
6048,00
|
|
13
|
6326,00
|
6432,00
|
|
26
|
6470,00
|
5904,00
|
|
9
|
6566,00
|
6192,00
|
|
4
|
6614,00
|
6720,00
|
|
28
|
6758,00
|
6000,00
|
|
17
|
6806,00
|
6144,00
|
|
6
|
6950,00
|
5760,00
|
|
14
|
6950,00
|
7008,00
|
|
25
|
6950,00
|
6240,00
|
|
7
|
7142,00
|
7776,00
|
|
31
|
7430,00
|
6240,00
|
|
18
|
7526,00
|
7296,00
|
|
10
|
7574,00
|
7728,00
|
|
20
|
7622,00
|
6240,00
|
|
24
|
7766,00
|
7152,00
|
|
29
|
7814,00
|
6576,00
|
|
15
|
7958,00
|
8496,00
|
|
12
|
8294,00
|
8160,00
|
|
21
|
8486,00
|
8400,00
|
|
16
|
9110,00
|
9120,00
|
III. Выводы по результатам выполнения лабораторной
работы.
Задача 1. Установление наличия стохастической связи между
факторным признаком Х и
результативным признаком Y:
а) графическим методом.
Вывод:
На основе анализа диаграммы рассеяния из Лабораторной работы №1, полученной после удаления
аномальных значений, можно сделать вывод, что имеет место стохастическая связь.
Предположительный вид связи: линейная прямая
б) методом сопоставления параллельных рядов.
Вывод: Табл.2.1, полученная путем
ранжирования предприятий по возрастанию значения факторного признака Х, показывает, что с увеличением
значений факторного признака увеличиваются значения результативного признака,
за исключением некоторых отклонений от общей тенденции, что позволяет сделать
вывод о наличии связи между признаками – прямая.
Задача 2. Установление наличия корреляционной связи
между признаками Х и Y методом аналитической группировки.
Вывод: Результаты выполнения аналитической
группировки предприятий по факторному признаку Среднегодовая стоимость основных производственных фондов даны в
табл. 2.2 Рабочего файла, которая показывает, что большое число предприятий
находится в промежутке от 6230 до 7190 млн.руб., где выпуск продукции
составляет 70224 млн. руб, и составляет 6384 млн руб. на одно предприятие в
среднем. Межу двумя представленными признаками существует прямая связь.
Задача 3.Оценка тесноты связи признаков Х и
Y:
а) на основе эмпирического корреляционного отношения.
Для анализа тесноты связи
между факторным и результативным признаками, рассчитывается показатель η - эмпирическое корреляционное
отношение, задаваемое формулой
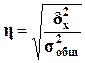 .
.
Для вычисления η необходимо знать общую дисперсию
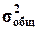 = 1854210,56 и
межгрупповую дисперсию
= 1854210,56 и
межгрупповую дисперсию 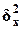 =1511155,2 результативного признака Y - Выпуск продукции.
=1511155,2 результативного признака Y - Выпуск продукции.
Результаты выполненных расчетов представляются табл.
2.4 Приложения 1
Вывод: Величина η= 0,81 является
близкой к единице, что свидетельствует о тесной связи между факторным и
результативным признаками.
б) на основе линейного коэффициента корреляции
признаков.
В предположении, что связь
между факторным и результативным признаками прямолинейная, для определения
тесноты связи на основе линейного коэффициента корреляции r был использован инструмент Корреляция надстройки Пакет анализа.
Результатом работы
инструмента Корреляции является
табл. 2.5 Приложения 1
Вывод: Значение коэффициента корреляции r =
0,91лежит в интервале 0,9-0,99, что в соответствии со шкалой Чэддока, говорит о
весьма тесной связи между факторным и результативным признаками.
Так
как значение коэффициента корреляции r положительное, то связь между признаками прямая.
Посредством
показателя η
измеряется теснота связи любой формы,
а с помощью коэффициента корреляции r – только прямолинейная, следовательно, значения η и r совпадают только при наличии прямолинейной связи. В
теории статистики установлено, что если 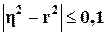 , то гипотезу о прямолинейной связи можно считать подтвержденной.
, то гипотезу о прямолинейной связи можно считать подтвержденной.
Вывод: т.к.
| 0,656-0,828| >= 0,1, значит, прямолинейная связь между факторным и
результативным признаком не подтверждается.
Задача 4. Построение однофакторной линейной регрессионной модели связи
изучаемых признаков с помощью инструмента Регрессия надстройки Пакет
анализа.
Построение регрессионной
модели заключается в определении аналитического выражения связи между факторным
признаком X и результативным признаком Y.
Инструмент Регрессия производит расчет параметров а0 и а1 уравнения однофакторной линейной регрессии 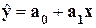 и проверку его адекватности исследуемым
фактическим данным.
и проверку его адекватности исследуемым
фактическим данным.
В результате работы
инструмента Регрессия были получены
результативные таблицы 2.6 – 2.9 Приложения 1.
Вывод: Однофакторная
линейная регрессионная модель связи факторного и результативного признаков
имеет вид прямой у= -1048,77+1,089х.
Доверительные интервалы коэффициентов уравнения регрессии
представлены в нижеследующей таблице:
|
Коэффициенты
|
Границы доверительных интервалов
|
|
с надежностью Р=0,68
|
с надежностью Р=0,95
|
|
Нижняя
|
Верхняя
|
Нижняя
|
Верхняя
|
|
а0
|
-1685,89
|
-411,65
|
-2329,72
|
232,18
|
|
а1
|
0,996
|
1,18
|
0,90
|
1,28
|
С увеличением надежности
границы доверительных интервалов расширяются
Экономическая интерпретация
коэффициента регрессии а1
выражается в формуле связи между вариацией факторного признака х и вариацией
результативного признака у.
Коэффициент
эластичности 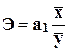 =1,089*(201300/187824)=1,167
=1,089*(201300/187824)=1,167
Экономическая интерпретация
коэффициента эластичности Э:
показывает на сколько процентов изменится в среднем
результативный признак при изменении факторного признака на 1%.
Задача 5. Нахождение наиболее адекватного уравнения регрессии
с помощью средств инструмента Мастер
диаграмм. Построение для этого уравнения теоретической линии регрессии.
Уравнения регрессии и их
графики построены для 4-х видов нелинейной зависимости между признаками и
представлены на диаграмме 2.1 Рабочего файла.
Уравнения регрессии и
соответствующие им коэффициенты детерминации R2 приведены в следующей таблице:
Регрессионные модели связи
|
Вид уравнения
|
Уравнение регрессии
|
Коэффициент
детерминации
R2
|
|
Полином
2-го порядка
|
y = 3E-18x2 + 1,0894x - 1048,8
|
1
|
|
Полином
3-го порядка
|
y = 3E-08x3 - 0,0006x2 + 5,0562x
- 8998,7
|
0,8381
|
|
Степенное
|
y = 0,1901x1,1797
|
0,8371
|
|
Экспоненциальное
|
y = 1792,9e0,0002x
|
0,8272
|
Выбор наиболее адекватного уравнения регрессии определяется
максимальным значением коэффициента детерминации R2: чем ближе значение R2
к единице,
тем более точно регрессионная модель соответствует фактическим данным
Вывод: Максимальное значение
коэффициента детерминации R2 =1
Вид искомого уравнения регрессии –полином 2-го порядка: y = 3E-18x2 + 1,0894x - 1048,8. Это уравнение регрессии и
его график приведены на отдельной диаграмме рассеяния таблицы 2.2 Приложения 1.
Вместе с тем,
так как значения коэффициентов детерминации кубического (R2) и линейного уравнения (η2), найденного с помощью
инструмента Регрессия надстройки Пакет анализа, расходятся очень
незначительно (на величину 0,172), а для показателей тесноты связи имеет место неравенство
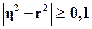 , то в качестве адекватного исходным данным уравнения
регрессии может быть принято линейное уравнение y
= 3E-18x2 + 1,0894x - 1048,8.
, то в качестве адекватного исходным данным уравнения
регрессии может быть принято линейное уравнение y
= 3E-18x2 + 1,0894x - 1048,8.