Всероссийский заочный финансово-экономический институт






КОНТРОЛЬНАЯ РАБОТА

по дисциплине «Финансовая математика»


Вариант №1



Исполнитель:

Специальность: Финансы и кредит

Группа:

№ зачетной книжки:

Преподаватель: Михайлов В.Н.






Москва

2007


Задание 1.

В каждом варианте приведены поквартальные данные о кредитах от коммерческого банка на жилищное строительство (в условных единицах) за 4 года (всего 16 кварталов, первая строка соответствует первому кварталу первого года).

Требуется:

1)      Построить адаптивную мультипликативную модель Хольта-Уинтерса с учетом сезонного фактора, приняв параметры сглаживания α1=0,3; α2=0,6; α3=0,3.

2)      Оценить точность построенной модели с использованием средней относительной ошибки аппроксимации.

3)      Оценить адекватность построенной модели на основе исследования:

·         случайности остаточной компоненты по критерию пиков;

·         независимости уровней ряда остатков по d-критерию (критические значения d1=1,10 и d2=1,37) и по первому коэффициенту автокорреляции при критическом значении r1=0,32;

·         нормальности распределения остаточной компоненты по R/S-критерию с критическими значениями от 3 до 4,21.

4)      Построить точечный прогноз на 4 шага вперед, т.е. на 1 год.

5)      Отразить на графике фактические, расчетные и прогнозные данные.



Решение:

Мультипликативная модель Хольта-Уинтерса с линейным ростом имеет следующий вид:

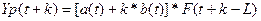
Коэффициенты модели рассчитываются по формулам:

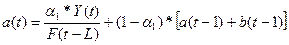
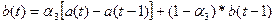
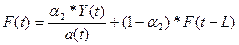
Для оценки начальных значений a(0) и b(0) построим линейную модель тренда временного ряда по первым восьми уровням Y(t).

Линейная модель имеет вид: y(t)=a+bt.

Коэффициенты a и b определяем методом наименьших квадратов по формулам:

 

 

 

 

t

Y(t)

t*Y(t)

y(t)

1

28

28

32,58333

2

36

72

33,45238

3

43

129

34,32143

4

28

112

35,19048

5

31

155

36,05952

6

40

240

36,92857

7

49

343

37,79762

8

30

240

38,66667

Σ

36

285

1319

63

ср.знач.

4,5

35,6

164,9

35,625






b(0)=

0,9

F(-3)=

0,859512

a(0)=

31,7

F(-2)=

1,079664



F(-1)=

1,27462

Yp(t)=31,7+0,9*t

F(0)=

0,785766

; ; ;

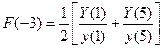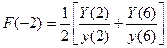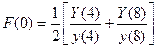
Далее вычисляем по формулам:

t

Y

a(t)

b(t)

F(t)

Yp(t)

0

 

31,7

0,9

0,785766

 

1

28

32,58132

0,868443

0,859438

28,00578

2

36

33,41794

0,858897

1,078225

36,11451

3

43

34,11445

0,810181

1,266126

43,68993

4

28

35,13745

0,874026

0,792429

27,44259

5

31

36,02906

0,879301

0,860025

30,94963

6

40

36,96525

0,896369

1,080548

39,79552

7

49

38,11336

0,97189

1,277833

47,93757

8

30

38,71716

0,861464

0,781882

30,97227

9

34

39,56516

0,857423

0,859615

34,03861

10

44

40,51182

0,884197

1,083881

43,67856

11

52

41,18538

0,821004

1,268684

52,89722

12

33

42,06623

0,838959

0,783439

32,84402

13

39

43,64437

1,060714

0,879998

36,88196

14

48

44,57915

1,022933

1,079594

48,45499

15

58

45,63646

1,033246

1,270022

57,85463

16

36

46,45417

0,968585

0,77835

36,56287

Для проверки точности модели вычисляем остатки:

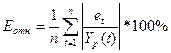
Квартал

Объем кредита

 

 

отн. погр-ть %

t

Y

Yp(t)

et

0

 

 

 

 

1

28

28,00578

-0,00578

0,02063387

2

36

36,11451

-0,11451

0,3180925

3

43

43,68993

-0,68993

1,60449915

4

28

27,44259

0,557413

1,99076144

5

31

30,94963

0,050374

0,16249833

6

40

39,79552

0,204478

0,51119446

7

49

47,93757

1,062429

2,16822255

8

30

30,97227

-0,97227

3,24091111

9

34

34,03861

-0,03861

0,11356266

10

44

43,67856

0,321445

0,73055605

11

52

52,89722

-0,89722

1,725418

12

33

32,84402

0,155981

0,47266899

13

39

36,88196

2,118044

5,43088329

14

48

48,45499

-0,45499

0,94790358

15

58

57,85463

0,145375

0,25064607

16

36

36,56287

-0,56287

1,56352389



Σ

21,2519759



ср.знач.

1,3282485

Еотн=1,33<15%, следовательно условие точности выполнено.

Для того, чтобы модель была адекватна исследуемому процессу, ряд остатков et должен обладать свойствами случайности, независимости последовательных уровней, нормальности распределения.

Проверку случайности уровней остаточной компоненты проводим на основе критерия поворотных точек. Для этого каждый уровень ряда et сравниваем с двумя соседними. Если он больше (либо меньше) обоих соседних уровней, то точка считается поворотной и для этой строки ставится 1, в противном случае ставится 0.

t

Y

Yp(t)

E(t)

точки поворота

E2(t)

(E(t)-E(t-1))2

E(t)*E(t-1)

0

 

 

 

 

 

 

 

1

28

28,00578

-0,00578

ххх

0,0000333793

 

 

2

36

36,11451

-0,11451

0

0,0131132959

0,01182348

0,000662

3

43

43,68993

-0,68993

1

0,4760097997

0,33110971

0,079007

4

28

27,44259

0,557413

1

0,3107094799

1,55587663

-0,38458

5

31

30,94963

0,050374

1

0,0025375885

0,25708826

0,028079

6

40

39,79552

0,204478

0

0,0418111646

0,02374783

0,0103

7

49

47,93757

1,062429

1

1,1287554806

0,73608037

0,217243

8

30

30,97227

-0,97227

1

0,9453154338

4,14001378

-1,03297

9

34

34,03861

-0,03861

0

0,0014908328

0,87172478

0,037541

10

44

43,67856

0,321445

1

0,1033266699

0,1296403

-0,01241

11

52

52,89722

-0,89722

1

0,8049989917

1,48513712

-0,28841

12

33

32,84402

0,155981

0

0,0243299999

1,1092263

-0,13995

13

39

36,88196

2,118044

1

4,4861124350

3,84969403

0,330374

14

48

48,45499

-0,45499

1

0,2070192827

6,62052558

-0,9637

15

58

57,85463

0,145375

1

0,0211338100

0,36044226

-0,06614

16

36

36,56287

-0,56287

ххх

0,3168210605

0,5016086

-0,08183



Σ

10

8,8835187049

21,983739

-2,26678

Общее число поворотных точек p=10. Рассчитаем значение q:

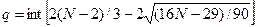
При N=16 – q=6. Так как p>q, условие случайности уровней ряда остатков выполнено.

Проверка независимости уровней ряда остатков проводим двумя методами:

1)      по d-критерию Дарбина-Уотсона;

2)      по первому коэффициенту автокорреляции r1.


1)

4-d=1,53

Т.к. 1,1<1,37<1,53<2, то уровни ряда остатков являются независимыми.

2) 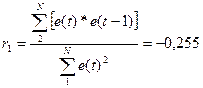, |r1|=0,255.

Так как |r1|<rтаб=0,32, то уровни ряда остатков независимы.

Нормальность распределения ряда остатков определяем по RS-критерию:

,

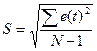
Emax=

2,118044484

Emin=

-0,972273333

S=

0,769567788


RS=

4,015653806

3<RS<4,21, значит уровни ряда остатков подчиняются нормальному распределению.

Таким образом, все условия адекватности и точности выполнены. Следовательно, можно говорить об удовлетворительном качестве модели и возможности проведения прогноза показателя Yp(t) на четыре квартала вперед.

t

Y

a(t)

b(t)

F(t)

Yp(t)

0

 

31,7

0,9

0,785766

 

1

28

32,58132

0,868443

0,859438

28,00578

2

36

33,41794

0,858897

1,078225

36,11451

3

43

34,11445

0,810181

1,266126

43,68993

4

28

35,13745

0,874026

0,792429

27,44259

5

31

36,02906

0,879301

0,860025

30,94963

6

40

36,96525

0,896369

1,080548

39,79552

7

49

38,11336

0,97189

1,277833

47,93757

8

30

38,71716

0,861464

0,781882

30,97227

9

34

39,56516

0,857423

0,859615

34,03861

10

44

40,51182

0,884197

1,083881

43,67856

11

52

41,18538

0,821004

1,268684

52,89722

12

33

42,06623

0,838959

0,783439

32,84402

13

39

43,64437

1,060714

0,879998

36,88196

14

48

44,57915

1,022933

1,079594

48,45499

15

58

45,63646

1,033246

1,270022

57,85463

16

36

46,45417

0,968585

0,77835

36,56287

17

 

 

 

 

41,73191

18

 

 

 

 

52,24301

19

 

 

 

 

62,68817

20

 

 

 

 

39,1732

При расчете Yp(17), Yp(18,) Yp(19), Yp(20) подставляем a(16) и b(16).

На графике покажем фактические, расчетные и прогнозные данные:



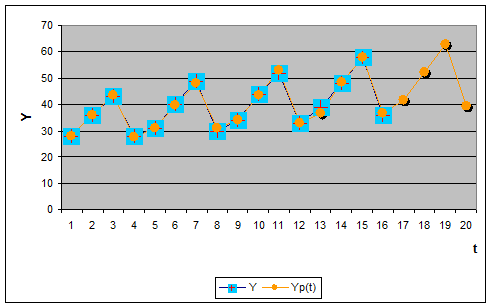
Задание 2.

Даны цены (открытия, максимальная, минимальная и закрытия) за 10 дней. Интервал сглаживания принять равным пяти дням. Рассчитать:

·         экспоненциальную скользящую среднюю;

·         момент;

·         скорость изменения цен;

·         индекс относительной силы;

·         %R, %K и %D.

Расчеты проводить для всех дней, для которых эти расчеты можно выполнить на основании имеющихся данных.



Решение.

Дни

Цены

 

 

 

макс.

мин.

закр.

ЕМА

MOM

ROC

1

998

970

982

 

 

 

2

970

922

922

 

 

 

3

950

884

902

 

 

 

4

880

823

846

 

 

 

5

920

842

856

901,6

 

 

6

889

840

881

894,7333333

-101

89,71486762

7

930

865

870

886,4888889

-52

94,36008677

8

890

847

852

874,9925926

-50

94,45676275

9

866

800

802

850,6617284

-44

94,79905437

10

815

680

699

800,1078189

-157

81,6588785







α=

0,333333





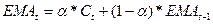, Ct – цена закрытия t-го дня

,

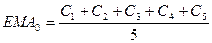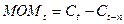, n=5

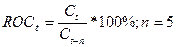
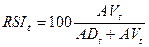
где AV и AD сумма приростов и убыли конечных цен за 5 дней.

Дни

цена закр.

повыш. цены за день

пониж. цены за день

AV

AD

AV+AD

RSI

1

982

 

 

 

 

 

 

2

922

0

60

 

 

 

 

3

902

0

20

 

 

 

 

4

846

0

56

 

 

 

 

5

856

10

0

 

 

 

 

6

881

25

0

35

136

171

20,46784

7

870

0

11

35

87

122

28,68852

8

852

0

18

35

85

120

29,16667

9

802

0

50

35

79

114

30,70175

10

699

0

103

25

182

207

12,07729

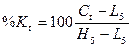
Ct - цена закрытия текущего дня t

L5, H5 – минимальная и максимальная цены за 5 предшествующих дней, включая текущий.

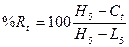
Дни

макс.

мин.

закр.

H5

L5

C-L5

H5-L5

H5-C

%K

%R

Σ(C-L5)

Σ(H5-L5)

%D

1

998

970

982

 

 

 

 

 

 

 

 

 

 

2

970

922

922

 

 

 

 

 

 

 

 

 

 

3

950

884

902

 

 

 

 

 

 

 

 

 

 

4

880

823

846

 

 

 

 

 

 

 

 

 

 

5

920

842

856

998

823

33

175

142

18,85714

81,14286

 

 

 

6

889

840

881

970

823

58

147

89

39,45578

60,54422

 

 

 

7

930

865

870

950

823

47

127

80

37,00787

62,99213

138

449

30,73497

8

890

847

852

930

823

29

107

78

27,1028

72,8972

134

381

35,1706

9

866

800

802

930

800

2

130

128

1,538462

98,46154

78

364

21,42857

10

815

680

699

930

680

19

250

231

7,6

92,4

50

487

10,26694

Задание 3.

Выполнить различные коммерческие расчеты, используя данные, приведенные в таблице.

S

Tн

Тк

Тдн

Тлет

i

m

500000

21.01.2002

11.03.2002

180

4

0,1

2

Например, S означает некую сумму средств в рублях, Тлеет – время в годах, i – ставку в процентах и т.д. По именам переменных из таблицы необходимо выбрать соответствующие численные значения параметров и выполнить расчеты.

3.1 Банк выдал ссуду, размером S рублей. Дата выдачи ссуды – Тн, возврата – Тк. День выдачи и день возврата считать за один день. Проценты рассчитываются по простой процентной ставке i% годовых. Найти:

3.1.1) точные проценты с точным числом дней ссуды;

;

К=

365

I=

6712,3288

t=

49


3.1.2) обыкновенные проценты с точным числом дней ссуды;

K=

360

I=

6805,5556

t=

49


3.1.3) обыкновенные проценты с приблизительным числом дней ссуды;

K=

360

I=

6944,4444

t=

50


3.2 Через Тдн дней после подписания договора должник уплатит S рублей. Кредит выдан под i% годовых (проценты обыкновенные). Какова первоначальная сумма и дисконт?

;

S=

500000

P=

476190,48

t=

180

D=

23809,524

K=

360


3.3 Через Тдн дней предприятие должно получить по векселю S рублей. Банк приобрел этот вексель с дисконтом. Банк учел вексель по учетной ставке i% годовых (год равен 360 дням). Определить полученную предприятием сумму и дисконт.

;

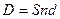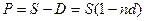
S=

500000

P=S-D=

475000

t=

180

D=

25000

K=

360

d=

0,1


3.4 В кредитном договоре на сумму S руб. и сроком на Тлет лет, зафиксирована ставка сложных процентов, равная i% годовых. Определить наращенную сумму.

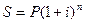
P=

500000

S=

732050

n=

4

i=

0,1


3.5 Ссуда, размером S руб. предоставлена на Тлет. Проценты сложные, ставка - i% годовых. Проценты начисляются m раз в году. Вычислить наращенную сумму.

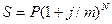
P=

500000

N=

8

n=

4

S=

738727,72

j=

0,1

m=

2


3.6 Вычислить эффективную ставку процента, если банк начисляет проценты m раз в году, исходя из номинальной ставки i% годовых.

j=

0,1

i=

0,1025

m=

2


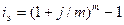
3.7 Определить, какой должна быть номинальная ставка при начислении процентов m раз в году, чтобы обеспечить эффективную ставку i% годовых.

i=

0,1

j=

0,0976177

m=

2


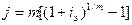
3.8 Через Тлеет предприятию будет выплачена сумма S руб. Определить ее современную стоимость при условии, что применяется сложная процентная ставка i% годовых.

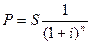
S=

500000

P=

341506,73

i=

0,1

n=

4


3.9 Через Тлет по векселю должна быть выплачена сумма S руб. Банк учел вексель по сложной процентной ставке i% годовых. Определить дисконт.

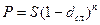
S=

500000

D=

171950

dсл=

0,1

n=

4


3.10 В течение Тлеет лет на расчетный счет в конце каждого года поступает по S  руб., на которые m  раз в году начисляются проценты по сложной годовой ставке i%. Определить сумму на расчетном счете к концу указанного срока.

n=

4

S=

2329050,9

R=

500000

j=

0,1

m=

2