Задание 1.

Построить модель заработной платы фирмы, в которой работают три человека: Гончаров В.П., Пятников С.В., Василевская З.Г. Данные для расчёта заработной платы за март месяц приведены в таблице:

Оклад, тыс. руб.	2,5	2,78	2,11
Премия, %	30	20	30
Кол. детей	2	0	2

Начисления с января месяца надо посчитать самим – это сумма начислений за январь и февраль месяцы.

При расчёте необходимо учесть, что Гончаров платит алименты на одного ребёнка. Рассчитывайте сумму алиментов и базу для расчёта подоходного налога, используя функцию ЕСЛИ. Построить график зависимости фамилии, подоходного налога и суммы к выдаче. Построить диаграмму зависимости фамилии, премии в рублях.

Решение:

Январь Февраль		Гончаров	Пятников	Василевская
Оклад	2,5	2,78	2,11
Алименты	0,45	0	0
Нал. база	2,05	2,78	2,11
Под. налог	0,27	0,36	0,27
Сумма к выдаче	1,78	2,42	1,84
В целом за два месяца	3,56	4,84	3,68

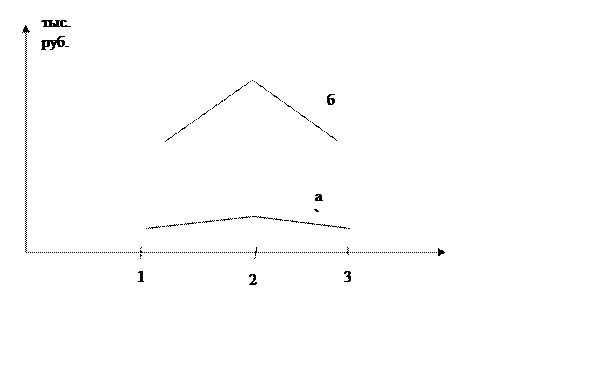
График зависимости фамилии, подоходного налога и суммы к выдаче:

27

а) график подоходных налогов;

б) сумма к выдаче.

1. Гончаров;

2. Пятников;

3. Василевская.

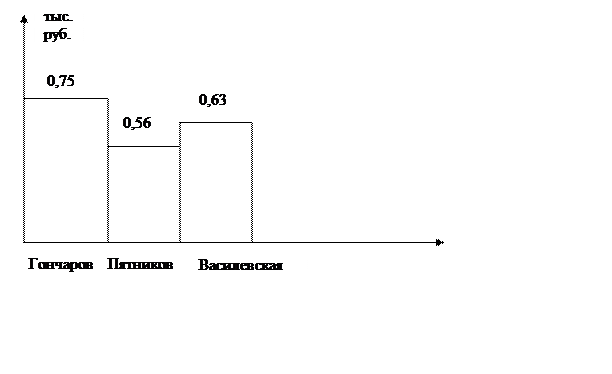
Диаграмма зависимости фамилии и премии.

Оклад Премия,%               руб	1	2	3
2,5	2,78	2,11
30	20	30
0,75	0,56	0,63

             

Задание 2.

Задача 1.

Для откорма крупного рогатого скота используется два вида кормов в₁ и в₂, в которые входят питательные вещества а₁, а₂, а₃, а₄. Содержание количеств единиц питательных веществ в одном килограмм каждого корма, стоимость одного килограмма корма и норма содержания питательных веществ в дневном рационе животного представлены в таблице. Составьте рацион при условии минимальной стоимости.

Питательные вещества	Вид корма	Норма содержания питательного вещества
В1	В2
а1	3	4	24
а2	1	2	18
а3	4	0	20
а4	0	1	6
Стоимость 1 кг корма, руб.	2	1

Решение:

Х₁ – количество корма в₁, кг;

Х₂ – количество корма в₂, кг.

 Ограничения по питательным веществам:

3х₁ + 4х₂ ≥ 24

х₁ + 2х₂ ≥ 18

4х₁ ≥ 20

х₂ ≥ 6

х₁, х₂ ≥ 0

Целевая функция:

Z = 2х₁ + х₂ → min

Построим область допустимых значений и отметим на графике grad Z:

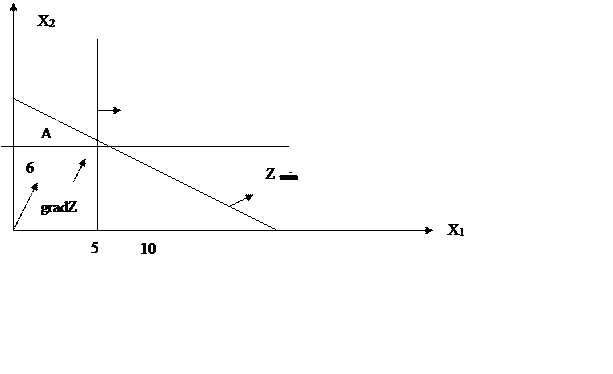Z _min соответствует (∙) А.

Найдём её координаты, решив систему уравнений:

х₁ + 2х₂ = 18 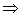                    х₁ = 5

х₁ = 5                                     х₂ = 6,5.

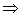 Рацион животных:

Корм в₁ : 5 кг

Корм в₂ : 6,5 кг

Затраты: Z = 2х₁ + х₂ = 10 + 6,5 = 16,5 руб.

Задача 2.

Трикотажная фабрика использует для производства свитеров и кофточек чистую шерсть, силон и нитрон, запасы которых составляют соответственно 800, 400 и 300 кг. Количество пряжи (кг), необходимое для изготовления 10 изделий, а также прибыль, получаемая от их реализации, приведены в таблице. Составьте план производства изделий, обеспечивающий получение максимальной прибыли.

Вид сырья в пряже	Затраты пряжи на 10 шт.
Свитер	Кофточка
Шерсть	4	2
Силон	2	1
Нитрон	1	1
Прибыль, руб.	6	5

Решение:

х₁ – объём производства свитеров (в 10 шт.);

х₂ – объём производства свитеров (в 10 шт.).

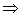 Ограничения по сырью:

4 х₁ + 2х₂ ≤ 800

2х₁ + х₂ ≤ 400

х₁ + х₂ ≤ 300

х₁, х₂ ≥ 0

Целевая функция:

Z = 6х₁ + 5х₂ → max

Построим область допустимых значений и отметим на графике grad z:

200                     300

Х2

Х1

Z_max соответствует точка А.

Найдём её координаты.

2х₁ + х₂ = 400 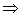                    х₁ = 0

х₁ = 0                                       х₂ = 400

 План производства:

Свитеры: 0 шт

Кофточки: 400 * 10 шт. = 4000 шт.

Прибыль:

Z_max = 6 х₁ + 5х₂ = 5 * 400 = 2000 руб.

Задание 3.

Задача 1.

Рассчитать, какая сумма окажется, если 10000 руб. положены на счёт в банке на 2 года под 8%. Проценты начисляются один раз в полгода.

Решение:

S (t) = S (0) * (1 + it)

i = 0,08     t = 2 * 2 = 4

S (0) = 10000

S (t) = 10000 * (1 + 0,08 * 4) = 13200 руб.

Ответ: 13200 руб.

Задача 2.

Рассчитать, в какой банк нам выгоднее вложить деньги, если мы хотим вкладывать по 15000 руб. в течении 2 лет. В один банк деньги можно вкладывать пренумерандо под 14% ., проценты начисляются ежеквартально. В другой банк деньги можно вкладывать постнумерандо под 14,5%, проценты начисляются ежеквартально.

Решение:

Для первого банка:

S₀ (m; n) = y *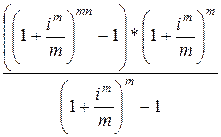

y = 15000

i = 0,14

n = 2

m = 4

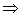 S₀ (4; 2) = 15000 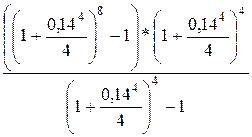 = 15000 *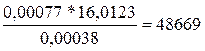

Для второго банка:

S₁ (m; n) = y *

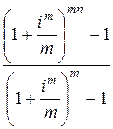
S₁ = 15000 *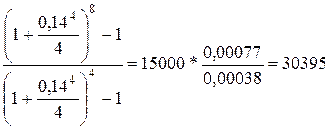

S₀ ≥ S₁ 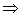  в первый банк выгоднее вкладывать деньги.

Задача 3.

Рассчитать, какая сумма окажется на вашем счёте через 3 года, если вы сначала сделали вклад в размере 2000 руб, а затем делали взносы постнумерандо по 1000 руб. Годовой процент – 14%, проценты в этом банке начисляются один раз в полгода.

Решение:

S₁ = y *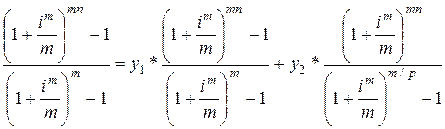

S₁ = 20000 *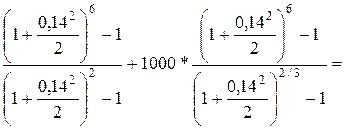

= 20000*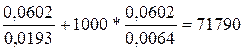 руб.