Всероссийский заочный финансово-экономический институт

Кафедра статистики

ОТЧЕТ

О результатах выполнения

компьютерной лабораторной работы № 2

«Автоматизированный априорный анализ

статистической совокупности в среде MS Excel»

Вариант № 95

Выполнила: студентка 3 курса, БУ, А и А

Проверил:

Омск - 2008 г.

1. Постановка задачи

Корреляционно-регрессионный анализ (КР-анализ) взаимосвязи признаков является составной частью проводимого статистического исследования двух экономических показателей статистической совокупности 32 предприятий и частично использует результаты Лабораторной работы №1.

В лабораторной работе №2 изучается взаимосвязь между факторным признаком среднегодовая стоимость основных фондов (признак Х) и результативным признаком Выпуск продукции (признак Y), значениями которых являются исходные данные Лабораторной работы №1 после исключения из них аномальных значений.

В процессе статистического исследования необходимо решить ряд задач.

1. Установить наличие статистический связи между факторным признаком Х и результативным признаком Y:

а) графическим методом;

б) методом сопоставления параллельных рядов.

2. Установить наличие корреляционной связи между признаками X и Y методом аналитической группировки.

3. Оценить тесноту связи признаков X и Y на основе:

а) эмпирического корреляционного отношения ;

б) линейного коэффициента корреляции r.

4. Построить однофакторную линейную регрессионную модель связи признаков X и Y. Используя инструмент Регрессия надстройки Пакет анализа.

5. Оценить адекватность и практическую пригодность построенной линейной регрессионной модели, указав:

а) доверительные интервалы коэффициентов а₀, а₁;

б) степень тесноты связи признаков X и Y.

в) погрешность регресионной модели;

6. дать экономическую интерпретацию:

а) коэффициента регрессии а₁;

б) коэффициента эластичности К_э;

7. Найти наиболее адекватное нелинейное уравнение регрессии с помощью средств инструмента Мастер диаграмм. Построить для этого уравнения теоретическую кривую регрессии.

Задание 1

Исходные данные
Номер предприятия	Среднегодовая стоимость основных производственных фондов, млн.руб.	Выпуск продукции, млн. руб.
5	4355,00	3395,00
23	4694,50	4510,50
27	5082,50	3880,00
1	5228,00	4995,50
8	5422,00	5335,00
32	5519,00	5626,00
22	5907,00	4801,50
19	6052,50	4607,50
2	6149,50	5480,50
3	6343,50	6111,00
13	6392,00	6499,00
26	6537,50	5965,50
9	6634,50	6256,50
4	6683,00	6790,00
28	6828,50	6062,50
17	6877,00	6208,00
6	7022,50	5820,00
14	7022,50	7081,00
25	7022,50	6305,00
7	7216,50	7857,00
31	7507,50	6305,00
18	7604,50	7372,00
10	7653,00	7808,50
20	7701,50	6305,00
24	7847,00	7226,50
29	7895,50	6644,50
15	8041,00	8584,50
12	8380,50	8245,00
21	8574,50	8487,50
16	9205,00	9215,00

				Таблица 2.2
Зависимость выпуска продукции от среднегодовой стоимости основных фондов
Номер группы	Группы предприятий по стоимости основеных фондов	Число предприятий	Выпуск продукции
Всего	В среднем на одно предприятие
1	4355-5325	4	16781,00	4195,25
2	5325-6295	5	25850,50	5170,10
3	6295-7265	11	70955,50	6450,50
4	7265-8235	7	50246,00	7178,00
5	8235-9205	3	34532,00	11510,67
Итого		30	198365,00	6612,166667


			Таблица 2.3
Показатели внутригрупповой вариации
Номер группы	Группы предприятий по стоимости основеных фондов	Число предприятий	Внутригрупповая дисперсия
1	4325-5325	4	369891,31
2	5325-6295	5	156753,94
3	6295-7265	11	319050,64
4	7265-8235	7	603520,14
5	8235-9205	3	169884,72
Итого		30	1619100,75


			Таблица 2.4
Показатели дисперсии и эмпирического корреляционного отношения
Общая дисперсия	Средняя из внутригрупповых дисперсия	Межгрупповая дисперсия	Эмпирическое корреляционное отношение
1893041,141	350239,5706	1542801,571	0,902765617

		Таблица 2.5
Линейный коэффициент корреляции признаков
	Стоимость основных фондов	Выпуск продукции
Стоимость основных фондов	1
Выпуск продукции	0,91318826	1

Выходные таблицы

ВЫВОД ИТОГОВ

Регрессионная статистика
Множественный R	0,91318826
R-квадрат	0,833912798
Нормированный R-квадрат	0,827981112
Стандартная ошибка	580,4030983
Наблюдения	30

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	1	47358937,1	47358937,06	140,5861384	1,97601E-12
Остаток	28	9432297,18	336867,7566
Итого	29	56791234,2

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 68,3%	Верхние 68,3%
Y-пересечение	-1059,81146	631,8627353	-1,677281158	0,104618054	-2354,125053	234,5021329	-1703,581261	-416,0416592
Переменная X 1	1,089355181	0,09187519	11,85690257	1,97601E-12	0,901157173	1,277553188	0,995748659	1,182961703

ВЫВОД ОСТАТКА
Наблюдение	Предсказанное Y	Остатки
1	3684,330353	-289,3303529
2	4054,166437	456,3335632
3	4476,836247	-596,836247
4	4635,337426	360,1625742
5	4846,672331	488,3276691
6	4952,339783	673,6602165
7	5375,009594	-573,5095937
8	5533,510773	-926,0107725
9	5639,178225	-158,6782251
10	5850,51313	260,4868698
11	5903,346856	595,6531435
12	6061,848035	-96,34803529
13	6167,515488	88,98451216
14	6220,349214	569,6507859
15	6378,850393	-316,3503929
16	6431,684119	-223,6841192
17	6590,185298	-770,185298
18	6590,185298	490,814702
19	6590,185298	-285,185298
20	6801,520203	1055,479797
21	7118,522561	-813,5225608
22	7224,190013	147,8099866
23	7277,02374	531,4762604
24	7329,857466	-1024,857466
25	7488,358645	-261,8586447
26	7541,192371	-896,692371
27	7699,69355	884,8064502
28	8069,529634	175,4703662
29	8280,864539	206,6354611
30	8967,70298	247,2970195

Выводы

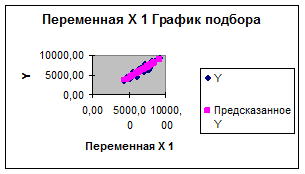
1. Между факторным признаком Х и результативным признаком Y присутствует статистическая связь. Связь между признаками имеет не случайный характер.

2. Наличие корреляционной связи между признаками X и Y методом аналитической группировки: эмпирическое корреляционное отношение равно = 0,902765617, линейный коэффициент корреляции 0,91318826

3. Теснота связи признаков X и Y: связь прямая, весьма высокая. На результативный признак также влияют и другие факторы.

4. Погрешность регрессионной модели: 631,8627353

5. Экономическая интерпретация коэффициента регрессии: с ростом стоимости основных фондов растет и выпуск продукции

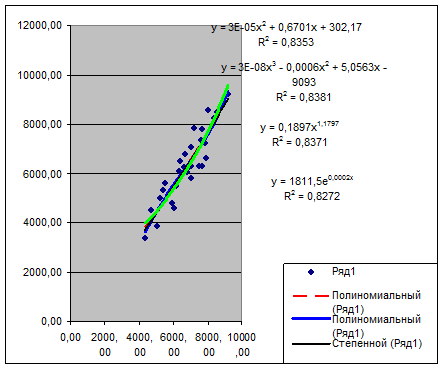
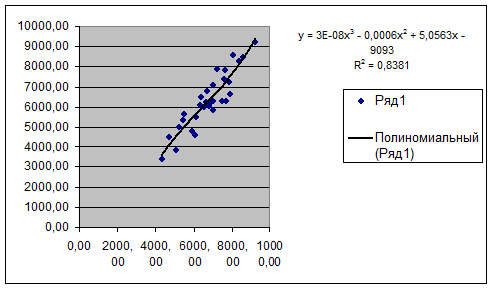
6. Наиболее адекватным нелинейным уравнением оказался полином третьей степени:

y = 3E-08x³ - 0,0006x² + 5,0563x - 9093

R² = 0,8381