1.
Достаточные признаки сходимости числового ряда
Числовой ряд а 1
+ а2 + … = 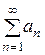 называется сходящимся,
если существует конечный предел
называется сходящимся,
если существует конечный предел 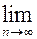
 Sn = S, где Sn = а1 + а2 + …
+ аn. В противном случае ряд называется расходящимся.
Sn = S, где Sn = а1 + а2 + …
+ аn. В противном случае ряд называется расходящимся.
Для определения
сходимости числовых рядов используется ряд признаков, позволяющих определить,
расходится данный ряд или сходится.
1.1. Признак сравнения
рядов.
Пусть имеем два ряда с
положительными членами:
а1 + а2
+ а3 + …
в1 + в2
+ в3 + …
Если для всех n Є [1, ∞) аn ≤ вn и ряд 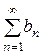 сходится, то сходится
ряд
сходится, то сходится
ряд 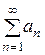 .
.
Этот признак сравнения
применяется только для рядов с положительными членами, этот признак перестаёт
быть верным, если среди членов ряда имеются отрицательные числа.
1.2. Признак Даламбера.
Если в ряде с
положительными членами а1 + а2 + а3 + …
отношение (n+1) – го члена к положительному при n → ∞ имеет конечный
предел l, т.е. 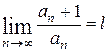 , то:
, то:
а) ряд сходится, если l ≤ 1;
б) ряд расходится, если l ≥ 1; если l = 1, то ответа на вопрос о сходимости
или расходимости ряда, признак не даёт.
Пример: Рассмотрим ряд
1 + 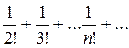
аn = 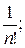 аn+1 =
аn+1 = 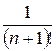

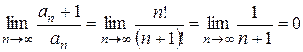
0 ≤ 1 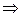 ряд
сходится.
ряд
сходится.
1.3. Признак Коши.
Если для ряда с
положительными членами а1 + а2 + а3 … величина
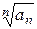 имеет конечный предел,
т.е.
имеет конечный предел,
т.е. 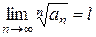 , то:
, то:
а) ряд сходится, если l ≤ 1;
б) ряд расходится, если l ≥ 1.
Случай l = 1 требует дополнительного
исследования, т.к. могут встретиться как сходящиеся, так и расходящиеся ряды.
Пример: Рассмотрим ряд
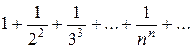
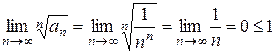
Ряд сходится.
1.4. Интегральный признак
Коши.
Пусть члены ряда а1
+ а2 + … + аn + … положительны и не возрастают, т.е. а1
≥ а2 ≥ а3 ≥ … ≥ аn ≥ … и пусть f(х) такая непрерывная и
невозрастающая функция, что f(1) = a1; f(2) = a2; … f(n) = an; … то:
а) если несобственный
интеграл 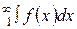 сходится, то ряд
сходится;
сходится, то ряд
сходится;
б) если 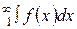 расходится, то ряд
расходится.
расходится, то ряд
расходится.
Пример: Рассмотрим ряд
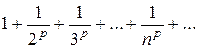
Тогда 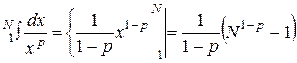
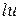 х
х 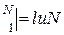 при р ≠ 1; при р = 1.
при р ≠ 1; при р = 1.
Устремляя N → ∞ получим:
При р ≥ 1 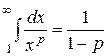 - ряд сходится;
- ряд сходится;
При р≤ 1 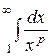 = ∞ - ряд
расходится;
= ∞ - ряд
расходится;
При р = 1 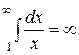 - ряд расходится.
- ряд расходится.
Кроме того, в ряде
случаев применяют признаки Рабе и Гаусса.
1.5. Признак Рабе: если
для ряда с положительными членами а1 + а2 + а3
+ … существует конечный предел: 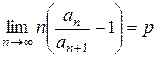 , то:
, то:
а) ряд сходится, если р
≥ 1;
б) ряд расходится, если р
≤ 1.
1.6. Признак Гаусса: если
все члены ряда а1 + а2 + а3 + … аn + …положительны и 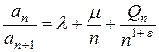 , где
, где 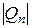 ≤ С; Е ≥ 0, то при
≤ С; Е ≥ 0, то при 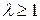 ряд сходится; при
ряд сходится; при 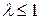 ряд сходится, если
ряд сходится, если 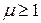 и расходится, если
и расходится, если 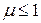 .
.
2. Нормальное распределение и его
характеристики.
Нормальный закон
распределения играет исключительную роль в теории вероятностей. Это наиболее
часто встречающийся закон распределения, главной особенностью которого то, что
он является предельным законом, к которому, при определённых условиях,
приближаются другие законы распределения.
Дифференциальная функция
нормального закона имеет вид:
f (x) = 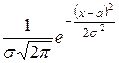
Числовые характеристики
нормального закона.
2.1. Математическое
ожидание характеризует центр распределения:
М (х) = 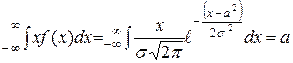
2.2. Дисперсия
характеризует форму распределения:
D (х) = 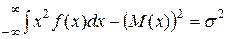 .
.
Свойства дифференциальной
функции нормального распределения.
а) область определения –
вся числовая ось;
б) ось ОХ –
горизонтальная асимптота;
в) х = а ± σ – точки
перегиба;
г) max функции в точке с координатами 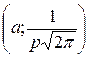 ;
;
д) график симметричен
относительно прямой х = а;
е) вероятность попадания
нормально распределённой случайной величины в заданный интервал определяется по
свойству интегральной функции: Р (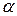 ≤ х ≤
β) = Ф*
≤ х ≤
β) = Ф* 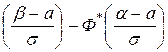 , где Ф* (х) =
, где Ф* (х) = 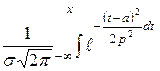 - интегральная функция нормального закона.
- интегральная функция нормального закона.
Свойства интегральной
функции нормального закона:
а) Ф* (-
∞) = 0;
б) Ф* (+
∞) = 1;
в) Ф* (х) = 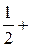 Ф (х);
Ф (х);
г) Ф* (- х) =
1 – Ф* (х).
Ф (х) – функция Лапласа.
Значения Ф*
(х) и Ф (х) приводятся в специальных таблицах.
3. Найти частное решение
дифференциального уравнения при данном начальном условии.
xy/ - 2y = x +1 y (0) =1
Решение:
Решаем данное уравнение
методом вариации переменной.
а) определяем общее
решение однородного уравнения:
xy/ - 2y = 0
xy/ = 2y
xdy = 2ydx
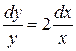
ln y = 2ln x + c;
ln C =C1
y = x2*C1
б) пусть u = u(x) – функция такая, что y = ux2 является решением исходного уравнения, тогда y/ = u/ x2 + 2ux.
Подставляем y и y/ в исходное уравнение:
X (u/ x2 + 2xu) – 2 ux2 = x+1
u/ x3 = x + 1
u/ = 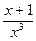
du = 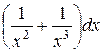
u = - 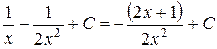
Тогда общее решение
уравнения:
Y = x2 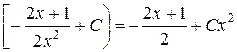
При х = 0 начальные
условия не выполняются, т.к. при х = 0, y = 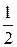 .
.

Проверим правильность
решения, подставим y и y/ в исходное уравнение:
y/ = - x + 2Cx
x (- 1 + 2 Cx) – 2 (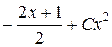 ) = - x + 2 Cx2 + 2x + 1 + Cx2 = x+1.
) = - x + 2 Cx2 + 2x + 1 + Cx2 = x+1.
Ответ: общее решение y = -  .
.
4. Дан ряд распределения
случайной величины х:
|
х
|
10
|
20
|
30
|
40
|
|
р
|
0,2
|
0,25
|
0,4
|
0,15
|
Найти: М (х), D (x), σ (х).
Решение:
Математическим ожиданием
дискретной случайной величины Х называют сумму произведений всех её возможных
значений на их вероятности.
М (х) = 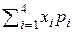 = 10 * 0,2 + 20 * 0,25 + 30 * 0,4 + 40 * 0,15 = 2 + 5 + 12 +
6 =25.
= 10 * 0,2 + 20 * 0,25 + 30 * 0,4 + 40 * 0,15 = 2 + 5 + 12 +
6 =25.
Дисперсией случайной
величины Х называют математическое ожидание квадратного отклонения случайной
величины от её математического ожидания.
D (x) = M (x – M (x))2
Дисперсию удобно
вычислять по формуле:
D (x) = M (x2) - [M (x)]2 = 100 * 0.2 + 400 * 0.25 + 900 * 0.4 + 1600 *0.15 – 252
= 20 + 100 + 360 + 240 – 625 = 95/
Среднее квадратическое
отклонение σ определяется по формуле:
σ = 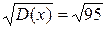 = 9,75.
= 9,75.
Ответ: М (х) = 25; D (x) = 95; σ (х) = 9,75.