2

2.Метод наименьших квадратов

Наилучшей кривой из всех кр явл та, для которой сумма квадратов отклонений исходных значений yt и модельных 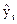значения явл наименьшей. Это принцып наименьших квадратов, леж в основе м. наименьших квадратов

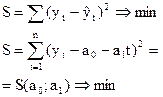
Ф-я S имеет экстремум в той точке, в кот частные производные обращ в 0

Найдем частн произв

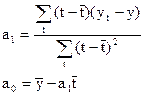
3.Открытая и закрытая модели транспортной задачи

Если 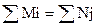задача закрытая

Если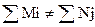 задача открытая

Любую открытую задачу сводим к закрытой путем введения фиктивного поставщика и потребителя. Mi-мощность поставщика, Nj-спрос потребителя

Mф=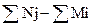

4.Канонический вид ЗЛП

ЗЛП назыв заданной в каноническом виде, если система ограничений ее явл системой ур-ний с неотриц правыми частыми. Любое нер-во можно привести к ур-нию путем введения в него любой дополнительной неотрицательной переменной.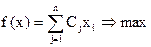

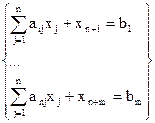
5.Прогнозирование при помощи кривой роста

Для получения прогнозных значений подставим в модель вместо t последующие значения. k-шаг прогноза; t=n+k (точечный прогноз)

Вероятность того, что точечный прогноз сбудется =0, поэтому строим интервальный прогноз. uk-ширина доверительного интервала

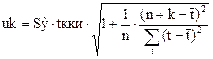где Sy – средняя квадр ош модели

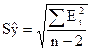t крит =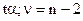

6.Графический метод решения ЗЛП

Необходимо:

1. построить множество решений сис ограничений. В общем случае реш-ем явл выпуклый многоугольник n-мерного пространства. Любая точка многоуг-ка явл допустимым решением.

Находим оптимальный план. Точки многоугольника в кот ф-я цель принимает к-л определенное значение f(x)=a. Эти точки располагаем на прямой наз. линией уровня. При f(x)=а линия уровня пройдет параллельно (0;0). Имея 2-е линии уровня достаточно, чтобы определить направление вектора-градиента. Перемещаем лин уровня до той

7.Выбор наилучшей кривой роста: метод конечных разностей.

Суть м.: для данного ряда нах абс приросты 1-го 2-го k-го порядка. Для каждого исходного ряда, а т ж для приростового р вычисляют дисперсию. Каждое очередное вычисленное значение дисперсии сравн с предыдущим. Наилучшим выравнивающим полиномом будет полином k^-1 если S²_k_-1 = S²_k М. Т. позволяет определить наилучш. выравн. кривую только среди полиномиальных кр.

8.Особые случаи решения ЗЛП

графически

1. оптимальное решение задачи единственно

2. оптимальное решение существует и не одно

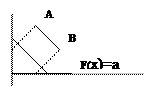fmax=f(А)=f(B)=f(AB)

3. ф-я-цель не ограничена

Если у многоугольника решений нет, то система противоречива, следовательно ЗЛП противоречива

10.Методы определение наличия

Тренда ФОСТЕРА-Стюарта.

1. метод проверки разности средних уровней (метод «Земских статистик»)

вр.р. делится на 2 примерно равные по кол-ву ур-ней части. Для каждой части вычисляют ср. ариф. и дисперсию. Большую дисп. делят на меньшую и получают расчетное значение критерия Фишера. F расч сравнивают с F Крит (из таблицы), если Fрасч <Fкрит, делаем вывод о равенстве дисперсий этих двух частей вр.р.

2. Знаковый критерий Кокса и Стюарта

3. Метод Фостера-Стюарта. Применяют для рядов с любой тенденцией. Для каждого уровня ряда, начиная со второго вычисляются величины: kt и lt. Kt = 1 если yt > всех предыдущих уровней, kt = 0 в ост. случ. Lt =1 если yt < всех пред. Уровней, =0 в ост. случ. Значения величин: st=kt+lt; dt=kt-lt. Находим сумму s и d. t расч для s = 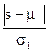; t расч для d = 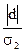, где … табличные значения. Каждое t расч сравн. с t крит. Если t расч для s > t крит. То есть тренд у дисперсии ряда. Если t расч для d > t крит, то есть тренд.

15.Предварительный анализ вр.р.

Анализ вр.р. начин. С выявления аномальных наблюдений.

Причины вызвавшие аномальные наблюдения:

1. заведомо подготовленные аном. набл.

2. ошибки вызванные неверной передачей статистич. Информации

Подлежат устранения:

1. ошибки второго рода носят объективный хар-р. АН возникшие из-за этих ошибок устранению не подлежат. Для выявления АН используются методы:

метод Ирвина (для каждого уровня ряда начиная со 2-го вычисляют 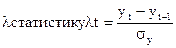где 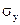- средн. кв. откл. в данном вр.р.

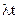сравнивают 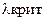(кот. нах. по таблице)

если 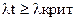, то наблюдение с номером t явл-ся аномальным, в противном случае yt неаном. набл. После обнаружения аном. набл. выясн. его причину.

24.2 теорема двойственности

(О дополняющей нежесткости)

Если при подстановке компонентов оптимального плана в систему ограничений исходной задачи i-е ограничение обращается в равенство, то i-я компонента др. з. положительна.

Если i-я компонента дв. з. =0, то i-е ограничение прямой задачи выполняется, как строгое нер-во.

17.Сглаживание временных рядов

1. Простая скользящая средняя.

Выбирают интервал сглаживания (кол-во ур-ней берут нечетное). 1-й сглаженный уровень придется на середину интервала сглаживания. Недостатки: Ур-ни равноправны по отношению к сглаженному ур-ю; в процедуре сглаживания участвуют не только предыдущие но и последующие ур-ни ряда; теряются p-первых и p – последних уровней ряда, где

2. Метод взвешенной скользящей средней

Уровни ряда входящие в интервал сглаживания берутся с некоторым определенным весом. Например для m=5 эти веса -3, 12, 17, 12, -3; Для m=3 … 1,2,1. Недостатки те же.

3. Метод экспоненциальной скользящей средней.

Сглаживание свободных от недостатков прост с.с. и взв. с.с. Сглаженный уровень ряда нах по формул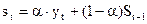е: , где параметр сглаживания. 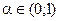принадлежит интервалу, если 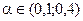явл наилучшим Нах методом подбора.

22.Алгоритм получения задачи, двойственной данной.

Исходя из св-в:

1. число переменных одной задачи = числу ограничений др. задачи.

2. а одной ф-я max-ется , в др. находится min

3. коэф-ты при переменных в выр-нии функции цели одной задачи явл. Равными частями системы ограничений др. задачи.

4. система ограничений одной и др. задачи задается как система неравенств: нер-ва смысла <= при max, нер-ва >= при min

5. матрицы коэф-ов при переменных транспонированы относительно друг друга.

6. условия не отрицательности переменных сохр-ется у той и др. задачи.

Задачи отвечающие св-вам явл. симметричными взаимодвойственными, при этом одну из них наз. Прямой, вторую двойственной.

1. привести прямую задачу к исходной форме. Если в прямой задаче отыскивается max (знаки нер-ва <=) , для двойственной ищем min

2. написать расширенную матрицу прямой з.

3. транспонировать эту матрицу

4. записать условие двойственной задачи.

23.1 теорема двойственности

(Основная)

Если одна из задач имеет оптимальное решение, то др. задача также имеет оптимальное решение, функции цели = между собой, т.е. fmax=gmin

Если ф-я цели одной из задач не ограниченна, то условие др. з. противоречиво

25.3 теорема двойственности

(Об оценках) (она же 3-св-во ООО)

значения переменных yi в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов bi системы ограничений – нер-в прямой задачи на величину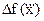

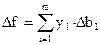
26 Свойства двойственных оценок и их использование для анализа оптимальных решений.

1.Величина двойственной оценки того или иного ресурса показывает насколько возросло бы максимальное значение ЦФ, если бы объем данного ресурса увеличился на одну единицу. (двойственные оценки измеряют эффективность малых приращений объемов ресурсов в конкретных условиях данной задачи). Это свойство позволяет выявить основные направления расшивки узких мест в производственной деятельности. 2.Двойственные оценки отражают сравнительную дефицитность различных видов ресурсов в отношении принятого в задаче показателя эффективности. Оценки показывают, какие ресурсы являются более дефицитными (они будут иметь самые высокие оценки), какие менее дефицитны и какие совсем не дефицитны. 3.Двойственные оценки позволяют определять нормы заменяемости ресурсов (предполагается неабсолютная заменяемость, а относительная, т.е. заменяемость с точки зрения критерия оптимальности). 4.Двойственные оценки служат инструментом определения эффективности отдельных хозяйственных решений. С их помощью можно определять выгодность производства новых изделий, эффективность новых технологических способов. ЕСЛИ ∆j = ∑ AijYi*- Cj ≤ 0 то выгодно, ЕСЛИ ∆j > 0 то невыгодно.

18.Особые случаи решения ЗЛП симплексным методом.

1ый особый случай решения ЗЛП: решение не единственное (линия уровня параллельна одной из линий на границе области допустимых решений). Это означает, что задача имеет бесконечное множество оптимальных решений. Его задают координаты точек отрезка с угловыми точками.

2ой особый случай решения ЗЛП – задача не имеет решения, т.к. область решений не ограничена сверху.

3ий особый случай решения ЗЛП – задача не имеет решения, т.к множество планов пусто, нет ни одной общей точки.

1. Статистические показатели динамики экономических процессов [1 стр.157-163].

2. Матрица планирования транспортной задачи, учет особых случаев [1 стр.100-02].

27.Хар-ка полиномиальных кривых роста

При помощи кр.р. производится прогнозирование (предсказание поведения показателя в будущем периоде по его поведению в прошлый и настоящий момент). Прогнозирование производится на основании построенной МатМодели вр.ряда.

Yt = a0+a1t. Найдем абсолютные приросты 1-го порядка для ut.

Ut(1)=yt+1-yt=(a0+a1(t+1))-(a0+a1t)=a1=const

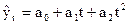абсолютные приросты 1-го порядка линейны относительно t

Найдем абс приросты 2-го порядка (приросты от приростов 1-го порядка)

Ut(2)=ut+1(1)-ut(1)=((a1+a2)+2a2(t+1))-((a1+a2)+2a2t)=2a2=const

Для полинома 2-й степени пост явл-ся абс приросты 2-го порядка

Для полинома k-ой степени пост будут абс приросты k-го порядка

21.Автокорелл.Дарбина-Уотсона)

Проверяется независимость последовательных уровней Et

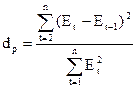
d расч сравн с двумя крит-ми уровнями. Знач-я крит-х ур-ней зависят от длины вр. р.

I-уровни зависимы; II – критерий не дает ответа; III – уровни независимы

I II III

0 0,8 1,36 2

Если dp>2, то треб доп исследование dp’=4-dp (больше 4-х не бывает)

r(1)-1-й коэффициент автокорреляции

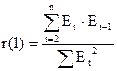если r(1) <0.36, то ур-ни независимы.

35.Точечный интервальный прогноз по м. Брауна

М. Б. не учитывает сезонную и циклическую компоненты (в ней только тренд и Et)

Для прогнозирования используем ур-ние с последнего шага. 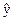= а₀+а₁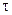, при 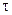=1, =2 (точечный прогноз)

Для интервального прогноза нужно рассчитать ширину доверительного интервала

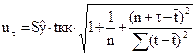
где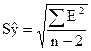

31.Хар-ка S-образных кривых роста

Если изменение эк-го показателя хар-ся sобразной кривой, то он в своем развитии проходит 4 этапа:

На 1 э абс приросты отсутствуют; на 2 э возрастают, на 3 постоянны, на 4 уменьшаются.

Из S образных кривых наиболее часто встречаются:

Кривая Гомперца; Кривая Перла-Рида; различные типы логистических кривых.

38.Базисные и опорные решения системы линейных уравнений, переход от одного базисного решения к другому.

В процессе решения системы уравнений на некотором этапе получилась расширенная матрица вида:

( 10…0А'1r+1…А'1n | B'1)

А'= ( 01…0A'2r+1…A'2n | B'2 )

(………………………|……)

(00….1A'rr+1…A'r n | B'r )

Система совместна и имеет бесчисленное множество решений. Общее решение системы записывают:

Х1= В'1-А'1r+1*Xr+1 ------A'1n*Xn

X2=B'2- A'2r+1*Xr+1-------A'2n*Xn

----------------------------------------------

Xr= B'r - A'rr+1*Xr+1--------A'r n*Xn

Придавая каждой из стоящих в правых частях равенств переменных Xr+1, Xr+2,……, Xn; произвольные значения, получаем частные решения системы. Неизвестные Х1, Х2,…., Хr; называют базисными или основными, они соответствуют линейно-независимым векторам А1, …, Аr. Любые r – переменных называют базисными, если определитель матрицы коэффициентов при них отличен от нуля, а остальные (n-r) переменных называют свободными или не основными. Базисным решением системы уравнений называют частное решение, в котором не основные переменные имеют нулевые значения. Каждому разбиению на основные и не основные переменные соответствует одно базисное решение, а количество способов разбиения не превышает величины Сⁿⁿn=n! /m!*(n-m)!

Если все компоненты базисного решения не отрицательны, то такое решение называют опорным. Любое частное решение получается из общего путем придания конкретных значений свободным переменным.

37.М-метод рещения ЗЛП

Симплекс-метод с искусственным базисом применяется в тех случаях, когда затруднительно найти первоначальный план опорный план КЗЛП. Этот метод заключается в применении правил симплекс-метода к М-задаче. Она получается из исходной добавлением к левой части векторного уравнения таких искусственных единичных векторов с соответствующими неотрицательными искусственными переменными, чтобы вновь полученная матрица содержала систему единичных, линейно-независимых векторов. В линейную форму исходной задачи добавляется в случае ее максимизации слагаемое, представляющее собой произведение числа (-М) на сумму искусственных переменных, где М –достаточно большое число. В полученной задаче первоначальный опорный план очевиден. При применении к этой задаче симплекс-метода оценки ∆j теперь будет зависеть от буквы М. Для сравнения оценок нужно помнить, что М- достаточно большое число. В процессе решения М-задачи следует вычеркивать в симплекс-таблице искусственные векторы по мере их выхода из базиса. Если все искусственные векторы вышли из базиса, то получаем исходную задачу. Если в оптимальном решении М-задачи хотя бы одна из искусственных переменных отлична от нуля, то система ограничений исходной задачи несовместна (задача неразрешима). В случае неразрешимости М-задачи будет неразрешима и исходная задача.

46.задача о назнач. транспортной задачи

Пусть задача закрытая, напишем мат модель. Обозначим кол-во груза перевез поставщиком I к потребителю j через xij

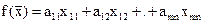достав бы min значением ф-ции f(x) и удовлетв системе ограничений