1. Функциональная и корреляционная зависимости.
Рассматривая зависимости между
признаками, необходимо выделить прежде всего две категории зависимости: 1) функциональные и 2) корреляционные.
Функциональные связи характеризуются полным соответствием между изменением
факторного признака и изменением результативной величины, и каждому значению
признака-фактора соответствуют
вполне определенные значения результативного признака. Функциональная зависимость может связывать результативный
признак с одним или несколькими факторными признаками. Так, величина начисленной заработной платы при повременной оплате труда зависит от количества
отработанных часов.
В корреляционных связях между изменением факторного и результативного признака
нет полного соответствия, воздействие отдельных факторов проявляется лишь в среднем при массовом наблюдении фактических
данных. Одновременное воздействие на изучаемый признак большого количества самых разнообразных факторов приводит к
тому, что одному и тому же значению признака-фактора соответствует целое распределение значений результативного
признака, поскольку в каждом конкретном случае прочие факторные признаки могут изменять силу
и направленность
своего воздействия.
При сравнении функциональных и
корреляционных зависимостей
следует иметь в виду, что при наличии функциональной зависимости между признаками
можно, зная величину факторного признака,
точно определить величину результативного признака. При наличии же корреляционной зависимости устанавливается лишь
тенденция изменения результативного признака при изменении величины факторного признака. В отличие от жесткости функциональной
связи корреляционные связи характеризуются множеством причин и следствий и устанавливаются лишь их тенденции.
2. Корреляционный
анализ, решаемые задачи с помощью корреляционного анализа.
Для двух переменных Х и У
теоретический коэффициент корреляции определяется следующим образом:
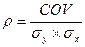 , где СOV– к-т ковариации Х и У, а σy и
σx –
стандартные отклонения. Он принимает значение в интервале (-1, +1). В
практических расчетах к-т корреляции генеральной
совокупности обычно неизвестен. По результатам выборки м.б. найдена его его точечная оценка – выборочн. к-т корреляции r, к-й является случайной величиной (т.к. выборочная
совокупность переменных Х и У случайна):
, где СOV– к-т ковариации Х и У, а σy и
σx –
стандартные отклонения. Он принимает значение в интервале (-1, +1). В
практических расчетах к-т корреляции генеральной
совокупности обычно неизвестен. По результатам выборки м.б. найдена его его точечная оценка – выборочн. к-т корреляции r, к-й является случайной величиной (т.к. выборочная
совокупность переменных Х и У случайна):
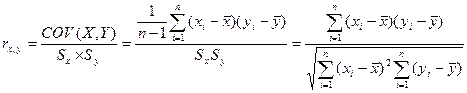 , где
, где 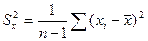 ,
, 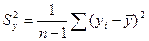 – оценки дисперсий Х и У.
– оценки дисперсий Х и У.
Для оценки значимости коэффициента корреляции
применяется t-критерий Стьюдента. При этом
фактическое значение этого критерия определяется по формуле: 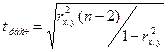
К-ты парной корреляции исп-ся
для измерения силы линейных связей различных пар признаков из их множества.
Получают матрицу к-в парной корреляции R
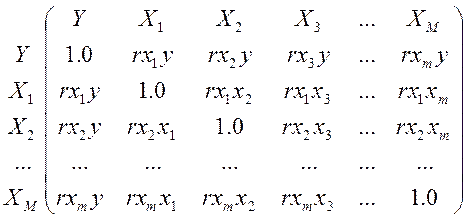
Одной корреляционной матрицей нельзя полностью описать
зависимости между величинами. В связи с этим в многомерном коррелицон.
анализе рассматриваются 2 задачи:
1) Определение тесноты связи одной случайной величины с
совокупностью остальных величин, включенных в анализ. Связь оценивается с пом. множествен. к-та корреляции:
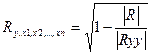 , где
, где 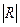 – определитель корреляц.матрицы ,
– определитель корреляц.матрицы , 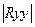 – алгебраическ.дополнение элемента ryy.
– алгебраическ.дополнение элемента ryy. 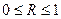 .
.
Проверка значимости к-та множеств.корреляции осущ-ся путем
сравнения расч и табл
значения к-та Фашера.:
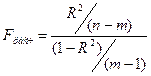
2) Определение тесноты связи между величинами при
фиксировании или исключении влияния остальных переменных. Оценивается с пом частн.к-та корреляции:
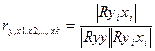 (r определяется в интервале от -1 до +1).
(r определяется в интервале от -1 до +1).
Кроме того, с помощью корреляционного анализа
решаются следующие задачи: отбор факторов, оказывающих наиболее существенное влияние на результативный признак, на
основании измерения степени связи между ними; обнаружение ранее неизвестных
причин связей. Корреляция непосредственно не выявляет причинных связей между
параметрами, но устанавливает численное значение этих связей и достоверность
суждений об их наличии.
3. Парная
корреляция. Оценка значимости коэффициента парной корреляции.
Для двух переменных Х и У
теоретический коэффициент корреляции определяется следующим образом:
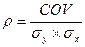 , где СOV– к-т ковариации Х и У, а σy и
σx –
стандартные отклонения.
, где СOV– к-т ковариации Х и У, а σy и
σx –
стандартные отклонения.
Парный
коэффициент корреляции является показателем тесноты связи лишь в случае линейной зависимости
между переменными и обладает следующими
основными свойствами. Коэффициент корреляции принимает значение в интервале (-1, +1). Коэффициент корреляции не зависит
от выбора начала отсчета и единицы
измерения. В практических
расчетах к-т корреляции генеральной совокупности
обычно неизвестен. По результатам выборки м.б. найдена его его
точечная оценка – выборочн. к-т
корреляции r, к-й
является случайной величиной (т.к. выборочная совокупность переменных Х и У
случайна):
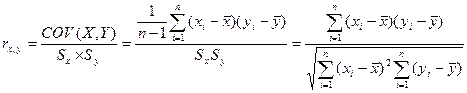 , где
, где 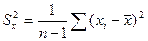 ,
, 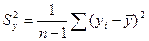 – оценки дисперсий Х и У.
– оценки дисперсий Х и У.
Для оценки значимости коэффициента корреляции
применяется t-критерий Стьюдента. При этом фактическое
значение этого критерия определяется по формуле: 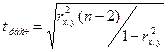
Вычисленное по этой формуле
значение tпабл сравнивается с критическим
значением t-критерия, которое берется из таблицы значений t
Стьюдента с учетом заданного уровня значимости и числа степеней свободы.
Если tмабл > tкр, то полученное значение
коэффициента корреляции признается значимым (т.е. нулевая гипотеза,
утверждающая равенство нулю коэффициента корреляции, отвергается). Отсюда
делается вывод, что между исследуемыми переменными есть тесная статистическая
взаимосвязь.
Если значение rу х
близко к
нулю, связь между переменными слабая. Если случайные величины связаны
положительной корреляцией, это означает, что при возрастании одной случайной
величины другая имеет тенденцию в среднем возрастать. Если случайные величины
связаны отрицательной корреляцией, это означает, что при возрастании одной
случайной величины другая имеет тенденцию в среднем убывать.
Коэффициенты парной
корреляции используются для измерения силы линейных связей различных пар
признаков из их множества. Для множества т признаков п наблюдений
получают матрицу коэффициентов парной корреляции R:
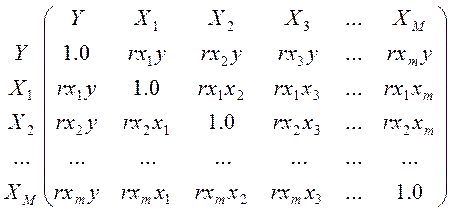
Одной корреляционной матрицей нельзя полностью описать
зависимости между величинами. В связи с этим в многомерном коррелицон.
анализе рассматриваются 2 задачи:
1. Определение
тесноты связи одной случайной величины с совокупностью остальных величин,
включенных в анализ.
2.
Определение тесноты связи между величинами при
фиксировании или исключении влияния остальных величин.
Эти
задачи решаются с помощью коэффициентов множественной и
частной корреляции соответственно.
4. Линейное
уравнение регрессии, коэффициенты модели.
Линейная
модель парной регрессии есть: у=а0+а1х+e
а1
- коэф-т регрессии, показывающий, как изменится у при
изменении х на единицу
а0
- это свободный член, расчетная величина, содержания нет.
e - это остаточная компонента, т.е. случайная величина,
независимая, нормально распределенная, мат ожид = 0 и
постоянной дисперсией.
В матричной форме модель имеет вид:
Y=XA+ε
Где Y–
вектор-столбец размерности (nx1) наблюдаемых значений зависимой переменной; Х–
матрица размерности (nx2) наблюдаемых значений факторных признаков.
Дополнительный фактор х0 вводится для вычисления свободного члена;
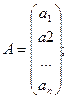
А– вектор-столбец размерности (2х1) неизвестных, подлежащих оценке
коэффициентов регрессии; ε– вектор-столбец
размерности (nх1) ошибок наблюдений
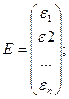
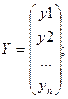

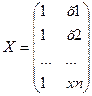 ;
; 
Параметры модели находятся с использованием МНК.
Подсчитывается сумма квадратов ошибок наблюдений.
5. Метод
наименьших квадратов.
Классический подход к
оцениванию параметров линейной регрессии основан на метода наименьших
квадратов. МНК позволяет получить такие оценки параметров а и Ь, при
которых
сумма квадратов отклонений фактических значений результативного признака (у)
от расчетных (теоретических) ух минимальна:
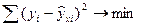
Иными словами, из свего множества линий линия регрессии на графике выбирается
так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией
была бы минимальной: 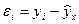 , следовательно,
, следовательно, 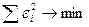
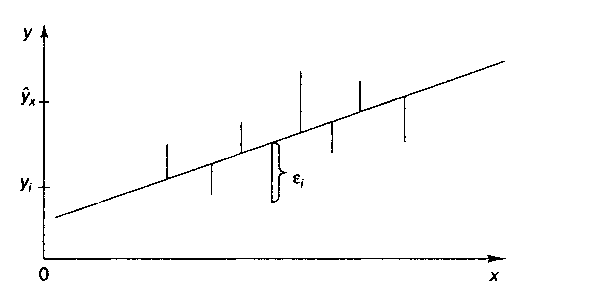
Чтобы найти минимум ф-ции 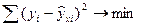 , надо вычислить частные производные по кажд.
из параметров а и b и приравнять их к
нулю. Обозначим
, надо вычислить частные производные по кажд.
из параметров а и b и приравнять их к
нулю. Обозначим 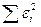 через S, тогда:
через S, тогда: 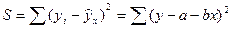 ;
;
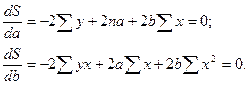
Преобразуя эту формулу, получим следующую систему
нормальных уравнений для оценки параметров а и b:
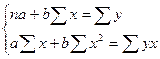
Решая эту систему нормальных уравнений либо методом
последовательного исключения переменных, либо методом определителей, найдем
искомые оценки параметров а и b. 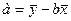 .
. 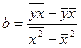
6.
Вычисление к-тов линейного уравнения регрессии.
Построение линейной регрессии
сводится к оценке ее параметров а и b. Оценки
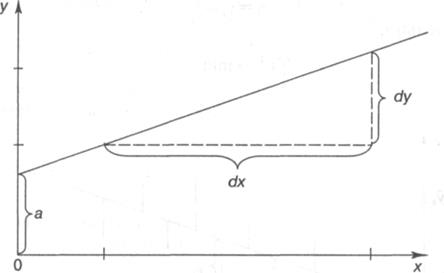
параметров линейной регрессии м.б. найдены разными способами. Можно обратиться к полю корреляции и, выбрав на графике две
точки, провести через них прямую
линию. Далее по графику можно определить значения параметров. Параметр а определим
как точку пересечения
линии регрессии с осью оу, а параметр b оценим, исходя из угла наклона линии регрессии,
как dу/dх, где dу — приращение результата у, а dх — приращение фактора х, т. е.
ух = а + b • х.
Классический подход к
оцениванию параметров линейной регрессии основан на метода наименьших
квадратов. МНК позволяет получить такие оценки параметров а и Ь, при
которых
сумма квадратов отклонений фактических значений результативного признака (у)
от расчетных (теоретических) ух минимальна:
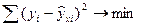
Иными словами, из свего множества линий линия регрессии на графике выбирается
так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией
была бы минимальной: 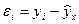 , следовательно,
, следовательно, 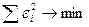
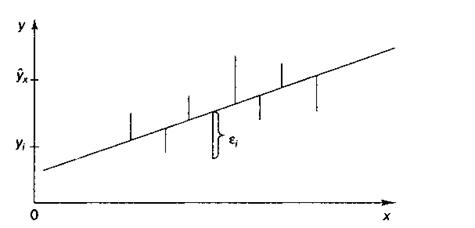
Чтобы найти минимум ф-ции 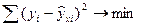 , надо вычислить частные производные по кажд.
из параметров а и b и приравнять их к
нулю. Обозначим
, надо вычислить частные производные по кажд.
из параметров а и b и приравнять их к
нулю. Обозначим 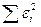 через S, тогда:
через S, тогда: 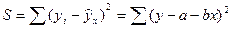 ;
;
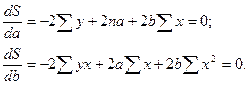
Преобразуя эту формулу, получим следующую систему
нормальных уравнений для оценки параметров а и b:
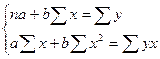
Решая эту систему нормальных уравнений либо методом
последовательного исключения переменных, либо методом определителей, найдем
искомые оценки параметров а и b. 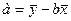 .
. 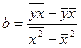
7. Оценка
адекватности модели прогнозирования.
Качество модели регрессии связывают с адекватностью модели наблюдаемым (эмпирическим) данным. Проверка адекватности (или соответствия) модели регрессии наблюдаемым данным проводится на основе анализа остатков – εi. При
построении уравнения регрессии мы можем разбить значение у в каждом наблюдении на 2 составляющие: 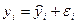 . Остаток представляет собой отклонение фактического значения зависимой
переменной от значения данной переменной, полученное расчетным путем:
. Остаток представляет собой отклонение фактического значения зависимой
переменной от значения данной переменной, полученное расчетным путем: 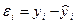 . Если εi=0, то
для всех наблюдений фактические значения зависимой переменной совпадают с расчетными (теоретическими)
значениями. Графически это
означает, что теоретическая линия регрессии
(линия, построенная по функции у=а0+а1х) проходит через все
точки корреляционного поля, что возможно только при строго
функциональной связи. Следовательно, результативный признак у полностью
обусловлен влиянием фактора х. На практике, как правило,
имеет место некоторое рассеивание точек корреляционного поля относительно
теоретической линии регрессии, т.е. отклонения эмпирических данных от теоретических (
. Если εi=0, то
для всех наблюдений фактические значения зависимой переменной совпадают с расчетными (теоретическими)
значениями. Графически это
означает, что теоретическая линия регрессии
(линия, построенная по функции у=а0+а1х) проходит через все
точки корреляционного поля, что возможно только при строго
функциональной связи. Следовательно, результативный признак у полностью
обусловлен влиянием фактора х. На практике, как правило,
имеет место некоторое рассеивание точек корреляционного поля относительно
теоретической линии регрессии, т.е. отклонения эмпирических данных от теоретических (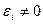 ). Величина этих отклонений и лежит в основе расчета
показателей качества (адекватности) уравнения.
). Величина этих отклонений и лежит в основе расчета
показателей качества (адекватности) уравнения.
для оценки качества регрессионных моделей используют также к-т
множественной корреляции: 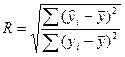 . Данный коэффициент является универсальным, т.к. он отражает
тесноту связи и точность модели, а также может использоваться при любой форме
связи переменных. Коэффициент множественной корреляции, возведенный в квадрат,
называется к-том детерминации:
. Данный коэффициент является универсальным, т.к. он отражает
тесноту связи и точность модели, а также может использоваться при любой форме
связи переменных. Коэффициент множественной корреляции, возведенный в квадрат,
называется к-том детерминации: 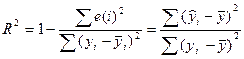 . Он показывает долю вариации результативного признака,
находящегося под воздействием изучаемых факторов, т.е. определяет, какая доля
вариации признака Y учтена в модели и обусловлена
влиянием на него факторов. Чем ближе он к 1, тем выше качество модели.
. Он показывает долю вариации результативного признака,
находящегося под воздействием изучаемых факторов, т.е. определяет, какая доля
вариации признака Y учтена в модели и обусловлена
влиянием на него факторов. Чем ближе он к 1, тем выше качество модели.
Для проверки значимости модели регрессии используется F-критерий Фишера, 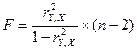
8. Оценка
точности модели, критерий Фишера
Для проверки значимости модели регрессии используется F-критерий Фишера. 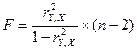 Если расчетное значение с t1=k и t2=(n-k-1) степенями свободы, где k– количество факторов, включенных в модель, больше
табличного при заданном уровне значимости, то модель считается значимой.
Если расчетное значение с t1=k и t2=(n-k-1) степенями свободы, где k– количество факторов, включенных в модель, больше
табличного при заданном уровне значимости, то модель считается значимой.
9.
Построение доверительного интервала для точечного прогноза по линейной модели.
Регрессионные модели м.б. использованы для
прогнозирования возможных ожидаемых значений зависимой переменной. Прогнозируемое
значение переменной у получается при подстановке в уравнение регрессии
ожидаемой величины фактора х. данный прогноз называется точечным. Значение
независимой переменной хпрогн не должно значительно отличаться от
входящих в исследуемую выборку, по которой вычислено уравнение регрессии.
Вероятность точечного прогноза теоретически равна 0. Поэтому рассчитывается
средняя ошибка прогноза или доверительный интервал прогноза с достаточно
большой надежностью. Доверительный интервалы зависят от стандартной ошибки,
удаления хпрогн от своего среднего значения, количества наблюдений и
уровня значимости прогноза. Определим доверительный интервал прогноза:
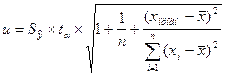
Величину отклонения от линии регрессии (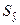 ) вычисляют по формуле:
) вычисляют по формуле:
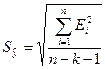
10. Оценка
точности модели. Среднее по модулю значение относительной ошибки.
В качестве меры точности модели применяют среднюю
относительную ошибку:
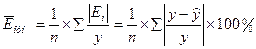
Этот показатель показывает, на сколько в среднем расчетные
значения для линейной модели отличаются
от фактических значений.
11.
Построение модели в виде гиперболической функции
Уравнение гиперболической модели имеет вид: 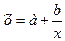
Проведем линеаризацию модели путем замены 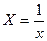 . В результате получим линейное уравнение:
. В результате получим линейное уравнение: 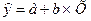
Рассчитаем его параметры:
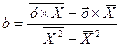
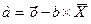
Получим следующее уравнение гиперболической модели:
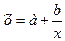
Далее проверяет качество модели (индекс корреляции, к-т детерминации, F-критерий
Фишера, средняя относительная ошибка).
12.
Построение модели в виде степенной функции.
Уравнение степенной модели имеет вид: 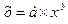 Для построения этой модели необходимо произвести линеаризацию
переменных. Для этого произведем логарифмирование обеих частей уравнения: lg
Для построения этой модели необходимо произвести линеаризацию
переменных. Для этого произведем логарифмирование обеих частей уравнения: lg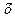 =lg a + b lg x
=lg a + b lg x
Обозначим Y= lg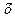 , X= lg x, A= lg a
, X= lg x, A= lg a
Тогда уравнение примет вид: Y=A+bX – линейное уравнение регрессии.
Определим коэффициенты уравнения по след формулам:
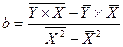
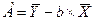
Перейдем к исходным переменным х и у, выполнив потенцирование данного уравнения:
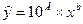
Получим уравнение степенной модели регрессии:
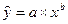
Далее проверяет качество модели (индекс корреляции, к-т детерминации, F-критерий
Фишера, средняя относительная ошибка).
13.
Построение модели в виде показательной функции.
Уравнение показательной модели имеет
вид: 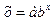
Для построения этой модели необходимо
произвести линеаризацию переменных. Для этого произведем логарифмирование обеих
частей уравнения: 
lg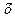 =lg a + x lg b
=lg a + x lg b
Обозначим Y= lg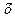 , B= lg b, A= lg a
, B= lg b, A= lg a
Получим линейное уравнение: Y=A+Вх.
Рассчитаем его параметры:
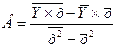
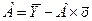
Перейдем к исходным переменным х и у, выполнив потенцирование данного
уравнения:
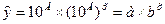
Далее проверяет качество модели (индекс корреляции, к-т детерминации, F-критерий
Фишера, средняя относительная ошибка).
16.Уравнение
линейной множественной регрессии, нахождение к-тов
модели.
Линейная модель множественной регрессии. У=а0+а1х1+
а2х2+…+ аmхm+e
Параметры определяются с помощью методов наименьших
квадратов.
Для этого
проведем все рассуждения в матричной форме. Введем следующие матричные обозначения:
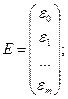


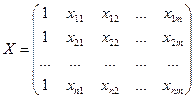 ;
; 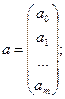
где У вектор n значений
результативного показателя.
Х – матрица n значений m независимых переменных; а матрица параметров
У=Х∙а+ε.
Заметим, что а – выборочные оценки совокупности.
Итак, метод наименьших квадратов
требует мин-ии суммы квадратов отклонений исходных
модели значений
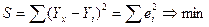 ,
, 
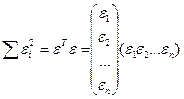
Далее: 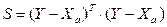
Из матричной алгебры известно, что 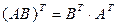 , тогда:
, тогда:
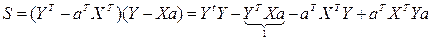
1 – это есть матрица размерностью 1Х1, т.е.
число-скаляр, а скаляр при трансформировании не меняется, поэтому 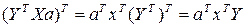 Þ
Þ 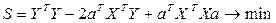
Согласно условию экстремума S по а =0
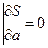 ;
; 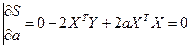
2ХТY+2aXTX=0
XTY=aXTX
Для погашения а умножим обе части этого уравнения на
(ХТХ)-1, тогда
а= (XTХ)-1∙XTY
Решение задачи нахождения матицы, а возможно лишь в
том случае, если строки и столбцы матрицы Х линейно независимы.
17.
Требования к исходным данным при построении многофакторных моделей.
Включение в
уравнение множественной регрессии того или иного набора факторов связано прежде всего с
представлением исследователя о природе взаимосвязи моделируемого показателя с другими
экономическими явлениями. Факторы, включаемые во множественную
регрессию, должны отвечать следующим требованиям.
1. Они должны быть
количественно измеримы. Если необходимо включить в модель качественный фактор,
не имеющий количественного измерения, то ему нужно придать количественную определенность
(например, в модели урожайности качество почвы задается в виде баллов; в модели
стоимости объектов недвижимости учитывается место нахождения недвижимости: районы могут быть проранжированы).
2. Факторы не должны
быть мультикоррелированы и тем более находиться в точной функциональной связи.
Включение в модель мультиколлениарный факторов, когда Ryx1 < Rx1x2 для зависимости у = а +
b1х1 + b2 х2 + е может привести к
нежелательным последствиям - система нормальных уравнений может оказаться плохо
обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии.
Если между факторами
существует высокая корреляция, то нельзя определить их изолированное влияние на
результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми. Так, в уравнении у =
а + b1х{ + b2 х2
+ е предполагается,
что факторы х, и х2 независимы друг от
друга, т. е. rx1x2 = 0. Тогда можно говорить, что параметр b1 измеряет силу влияния фактора х1
на результат у при неизменном значении фактора х2.
Если же rx1x2 =1, то с изменением фактора х1
фактор х2
не
может оставаться неизменным. Отсюда b1 и b2 нельзя интерпретировать как
показатели раздельного влияния х, и х2 и
на у.
18. Нахождение коэффициентов
многофакторной линейной модели прогнозирования.
Линейная модель множественной регрессии. У=а0+а1х1+
а2х2+…+ аmхm+e
Параметры определяются с помощью методов наименьших
квадратов.
Для этого
проведем все рассуждения в матричной форме. Введем следующие матричные обозначения:
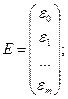


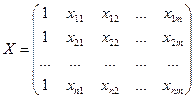 ;
; 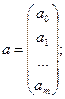
где У вектор n значений
результативного показателя.
Х – матрица n значений m независимых переменных; а матрица параметров
У=Х∙а+ε.
Заметим, что а – выборочные оценки совокупности.
Итак, метод наименьших квадратов
требует мин-ии суммы квадратов отклонений исходных
модели значений
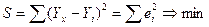 ,
, 
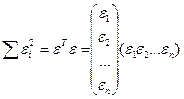
Далее: 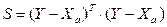
Из матричной алгебры известно, что 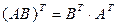 , тогда:
, тогда:
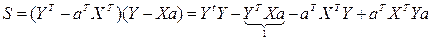
1 – это есть матрица размерностью 1Х1, т.е.
число-скаляр, а скаляр при трансформировании не меняется, поэтому 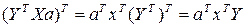 Þ
Þ 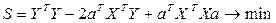
Согласно условию экстремума S по а =0
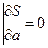 ;
; 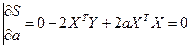
2ХТY+2aXTX=0
XTY=aXTX
Для погашения а умножим обе части этого уравнения на
(ХТХ)-1, тогда
а= (XTХ)-1∙XTY
Решение задачи нахождения матицы, а возможно лишь в
том случае, если строки и столбцы матрицы Х линейно независимы.
19. Система
нормальных уравнений для многофакторных моделей прогнозирования.
Параметры уравнения
множественной регрессии оцениваются, как и в парной регрессии, методом
наименьших квадратов (МНК). При его применении строится система нормальных уравнений, решение
которой и позволяет получить оценки параметров регрессии.
Так, для уравнения
система нормальных уравнений составит
Ее решение может быть
осуществлено методом определителей:
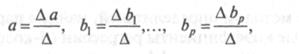 где Δ– определитель системы; Δа,Δb1,…,Δbp– частные определители.
где Δ– определитель системы; Δа,Δb1,…,Δbp– частные определители.
20. Линейное
уравнение множественной регрессии, вычисление статистических характеристик.
21. Оценка
адекватности уравнения множественной регрессии.
Для оценки качества модели множественной регрессии
вычисляют к-т монж.корреляции
R и детерминации R2.
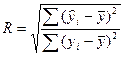 ;
;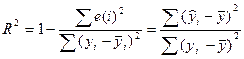 показывает долю
вариации результативного признака, находящегося под воздействием изучаемых
факторов, т.е. определяет, какая доля вариации признака Y учтена в модели и обусловлена влиянием на него
факторов.
показывает долю
вариации результативного признака, находящегося под воздействием изучаемых
факторов, т.е. определяет, какая доля вариации признака Y учтена в модели и обусловлена влиянием на него
факторов.
Чем ближе к 1 значение этих характеристик, тем выше
качество модели. В многофакторной регрессии добавление дополнительных
объясняющих переменных увеличивает к-т детерминации.
Следовательно, к-т детерминации д.б. скорректирован с
учетом числа независимых переменных. Скорректированный R2
рассчитывается так:
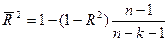 , где n– число
наблюдений, k– число независимых переменных.
, где n– число
наблюдений, k– число независимых переменных.
Для проверки значимости модели регрессии исп-ся F-критерий Фишера:
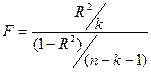 Если расчетное
значение с t1=k и t2=(n-k-1) степенями
свободы, где k– количество факторов, включенных
в модель, больше табличного при заданном уровне значимости, то модель считается
значимой.
Если расчетное
значение с t1=k и t2=(n-k-1) степенями
свободы, где k– количество факторов, включенных
в модель, больше табличного при заданном уровне значимости, то модель считается
значимой.
22. Оценка
значимости факторов по к-там эластичности и к-там корреляции.
К-т эластичности: 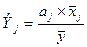 . Он показывает, на сколько % изменяется зависимая переменная
при изменении фактора j на 1%.
. Он показывает, на сколько % изменяется зависимая переменная
при изменении фактора j на 1%.
Показатель множественной корреляции характеризует
тесноту связи рассматриваемого набора факторов с исследуемым признаком, или,
иначе, оценивает тесноту совместного влияния факторов на результат. Независимо
от формы связи показатель множ.корреояции м.б. найден
как индекс множ.корреляции:
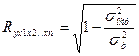 где
где 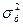 – общ.дисперсия результативн.признака,
– общ.дисперсия результативн.признака,
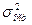 – остаточная досперсия для
уравнения. Границы его измерения: от 0 до 1. Чем ближе его значение к 1, тем
теснее связь результативного признака со всем набором исследуемых факторов.
– остаточная досперсия для
уравнения. Границы его измерения: от 0 до 1. Чем ближе его значение к 1, тем
теснее связь результативного признака со всем набором исследуемых факторов.
Частные к-ты (индексы)
корреляции хар-т тесноту связи между результатом и
соотв.фактором при устранении влияния др факторов,
включенных в уравнение регрессии.
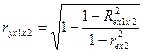
23.
Построение точечного прогноза для многофакторных моделей.
Прогнозируемое значение переменной у получается при
подстановке в уравнение регрессии ожидаемой величины фактора х. данный прогноз
называется точечным. Значение независимой переменной хпрогн не
должно значительно отличаться от входящих в исследуемую выборку, по которой вычислено
уравнение регрессии.
Доверительный интервал прогноза рассчитывается след.образом:
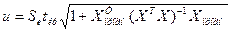
24. К-ты эластичности и бета-к-ты, их
смысл.
К-т эластичности: 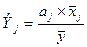 . Он показывает, на сколько % изменяется зависимая переменная
при изменении фактора j на 1%.
. Он показывает, на сколько % изменяется зависимая переменная
при изменении фактора j на 1%.
Бета-к-т:
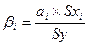 , где
, где 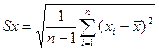 ;
;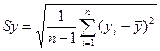 – среднеквадратические отклонения.
– среднеквадратические отклонения.
Бета-к-т показывает, на какую часть величины среднего
квадратического отклонения Sy тзменится зависимая
переменная Y с изменением соответствующий
независимой переменной Xj на величину среднеквадратического отклонения
при фиксированном на постоянном уровне значении остальных переменных.
25.
Вычисление к-та эластичности и бета-к-та.
К-т эластичности: 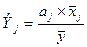 . Он показывает, на сколько % изменяется зависимая переменная
при изменении фактора j на 1%.
. Он показывает, на сколько % изменяется зависимая переменная
при изменении фактора j на 1%.
Бета-к-т:
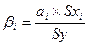 , где
, где 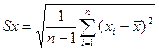 ;
;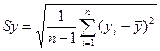 – среднеквадратические отклонения.
– среднеквадратические отклонения.
Бета-к-т показывает, на какую часть величины среднего
квадратического отклонения Sy тзменится зависимая
переменная Y с изменением соответствующий
независимой переменной Xj на величину среднеквадратического отклонения
при фиксированном на постоянном уровне значении остальных переменных.
26. К-т
детерминации и его смысл
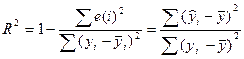 показывает долю
вариации результативного признака, находящегося под воздействием изучаемых
факторов, т.е. определяет, какая доля вариации признака Y учтена в модели и обусловлена влиянием на него
факторов.
показывает долю
вариации результативного признака, находящегося под воздействием изучаемых
факторов, т.е. определяет, какая доля вариации признака Y учтена в модели и обусловлена влиянием на него
факторов.
Чем ближе к 1 значение этих характеристик, тем выше
качество модели. В многофакторной регрессии добавление дополнительных
объясняющих переменных увеличивает к-т детерминации.
Следовательно, к-т детерминации д.б. скорректирован с
учетом числа независимых переменных. Скорректированный R2
рассчитывается так:
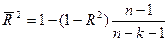 , где n– число
наблюдений, k– число независимых переменных.
, где n– число
наблюдений, k– число независимых переменных.
27. Оценка
устойчивости факторов по к-ту эластичности и бета-к-ту.
К-т эластичности: 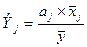 . Он показывает, на сколько % изменяется зависимая переменная
при изменении фактора j на 1%.
. Он показывает, на сколько % изменяется зависимая переменная
при изменении фактора j на 1%.
Бета-к-т:
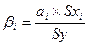 , где
, где 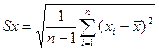 ;
;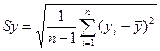 – среднеквадратические отклонения.
– среднеквадратические отклонения.
Бета-к-т показывает, на какую часть величины среднего
квадратического отклонения Sy тзменится зависимая
переменная Y с изменением соответствующий
независимой переменной Xj на величину среднеквадратического отклонения
при фиксированном на постоянном уровне значении остальных переменных.
28. Проверка
выполнения предпосылок регрессионного анализа.
Проверка выполнения
предпосылок регрессионного анализа выполняется на основе анализа остаточной
компоненты. Анализ остатков позволяет получить представление, насколько хорошо
подобрана сама модель и насколько правильно выбран метод оценки коэффициентов.
Согласно общим предположениям регрессионного анализа остатки должны вести себя
как независимые (в действительности почти
независимые) одинаково распределенные случайные
величины. В
классических методах регрессионного анализа предполагается также нормальный закон распределения остатков. Исследование остатков
полезно начинать с изучения их графика. Он может показать наличие какой-то
зависимости, не учтенной в модели. Скажем, при подборе простой линейной
зависимости между У и X график остатков может
показать необходимость перехода к нелинейной модели (квадратичной,
полиномиальной, экспоненциальной) или включения в модель периодических
компонент. График остатков хорошо показывает и резко отклоняющиеся от модели
наблюдения — выбросы. Подобным аномальным набдениям
надо уделять особо пристальное внимание, так как их присутствие может грубо
искажать значения оценок. Устранение эффектов выбросов может проводиться либо с
помощью удаления их точек из анализируемых данных (эта процедура называется цензурированием), либо с помощью применения методов
оценивания параметров, устойчивых к подобным грубым отклонениям.
Независимость остатков
проверяется с помощью критерия Дарбина—Уотсона.
Корреляционная зависимость
между текущими уровнями некоторой переменной и уровнями этой же переменной,
сдвинутыми на несколько шагов, называется автокорреляцией.
Автокорреляция случайной
составляющей нарушает одну из предпосылок нормальной линейной модели регрессии.
Наличие (отсутствие) автокорреляции в отклонениях проверяют с помощью критерия Дарбина—Уотсона. Численное значение коэффициента равно
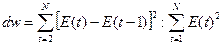
Значение dw статистики близко к величине 2(1 - г(1)), где г(1)
— выборочная автокорреляционная функция остатков первого порядка. Таким
образом, значение статистики Дарбина—Уотсона
распределено в интервале 0—4. Соответственно идеальное значение статистики — 2
(автокорреляция отсутствует). Меньшие значения критерия соответствуют
положительной автокорреляции остатков, большие значения — отрицательной.
Статистика учитывает только автокорреляцию первого порядка. Оценки, получаемые
по критерию, являются не точечными, а интервальными. Верхние (d2) и
нижние (d1)
критические значения, позволяющие принять или отвергнуть гипотезу об отсутствии
автокорреляции, зависят от количества уровней динамического ряда и числа независимых
переменных модели. Значения этих границ для уровня значимости α = 0,05 даны в специальных таблицах. При сравнении
расчетного значения dw статистики с табличным
могут возникнуть такие ситуации: d2 < dw < 2 — ряд остатков не
коррелирован; dw < d} —
остатки содержат автокорреляцию;
d1 < dw < d2 —
область неопределенности, когда нет оснований ни принять, ни отвергнуть
гипотезу о существовании автокорреляции. Если d превышает 2, то это
свидетельствует о наличии отрицательной корреляции. Перед сравнением с табличными
значениями dw критерий следует преобразовать по формуле dw' = 4 – dw.
Установив наличие
автокорреляции остатков, переходят к улучшению модели. Если же ситуация
оказалась неопределенной (d1 < dw< d2 ) применяют другие
критерии. В частности, можно воспользоваться первым коэффициентом
автокорреляции
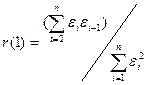
Для принятия решения о
наличии или отсутствии автокорреляции в исследуемом ряду фактическое значение
коэффициента автокорреляции r(1) сопоставляется с табличным (критическим) значением для 5%-ного
уровня значимости (вероятности допустить ошибку при принятии нулевой гипотезы
о независимости уровней ряда). Если фактическое значение коэффициента автокорреляции
меньше табличного, то гипотеза об отсутствии автокорреляции в ряду может быть
принята, а если фактическое значение больше табличного — делают вывод о наличии
автокорреляции в ряду динамики.
Обнаружение гетероскедастичности.
Для обнаружения гетеро-скедастичности
обычно используют три теста, в которых делаются различные предположения о
зависимости между дисперсией случайного члена и объясняющей переменной: тест ранговой
корреляции Спирмена, тест Голдфельда—
Квандта и тест Глейзера.
При малом объеме выборки для
оценки гетероскедастичности может использоваться
метод Голдфельда— Квандта.
Данный тест используется для
проверки такого типа гетероскедастичности, когда дисперсия
остатков возрастает пропорционально квадрату фактора. При этом делается
предположение, что случайная составляющая распределена нормально.
Чтобы оценить нарушение
гомоскедастичности по тесту Голдфельда— Квандта, необходимо выполнить следующие шаги.
1. Упорядочение п наблюдений по мере возрастания
переменной х.
2. Разделение совокупности на
две группы (соответственно с малыми и большими значениями фактора х) и определение по каждой из групп
уравнений регрессии.
3. Определение остаточной суммы
квадратов для первой регрессии 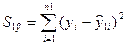 и второй регрессии
и второй регрессии 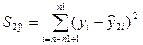
4. Вычисление отношений 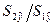 (или наоборот) в числителе д.б. сумма квадратов. Полученное
отношение имеет F распределение со степенями
свободы k1=n1–m и k2=n–n1–m (где m – число
оцениваемых парметров в уравнении регрессии).
(или наоборот) в числителе д.б. сумма квадратов. Полученное
отношение имеет F распределение со степенями
свободы k1=n1–m и k2=n–n1–m (где m – число
оцениваемых парметров в уравнении регрессии).
Если 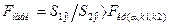 , то гетероскедастичность имеет
место.
, то гетероскедастичность имеет
место.
Чем больше величина F превышает табличное значение F-критерия, тем более нарушена предпосылка о равенстве
дисперсий остаточных величин.
29. Проверка
гипотезы о случайности ряда остатков.
Первая
предпосылка МНК– проверка случайного характера остатков. С этой целью строится
график зависимости остатков от теоретических значений результативного признака.
Если на графике получена горизонтальная полоса, то
остатки представляют собой случайные величины и МНК оправдан, теоретические
значения результативного признака хорошо аппроксимируют фактические значения у.
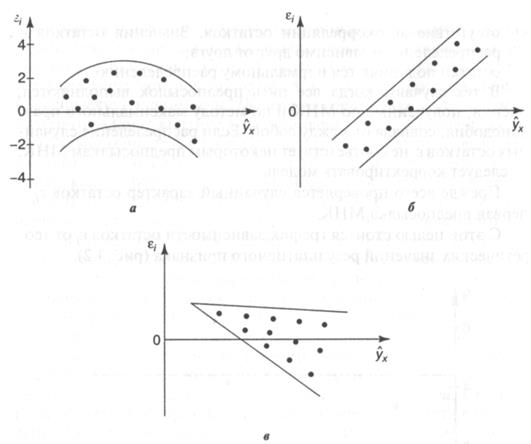
возможны следующие случаи: если остатки зависят от теоретических значений
результирующей переменной:
– остатки не случайны (рис. 3,3а)
– остатки не имеют постоянной дисперсии (в)
– остатки носят систематический характер (б), в данном
случае отрацательные значения остатков соответствуют
низким теоретическим значениям у, а положительные – высоким значениям. В случаях а), б), в) (рис.
3.3) необходимо либо применять другую функцию, либо вводить дополнительную информацию и заново строить
уравнение регрессии до тех пор, пока остатки е, не будут случайными величинами.
30. Проверка
гипотезы о нормальном распределении ряда остатков.
Нормальность распределения ряда остатков означает
однородность дисперсий наблюдения. Определяется с помощью R/S-критерия:
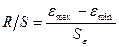 ; если
; если 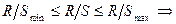 нормальный закон распределения остатков выполняется.
нормальный закон распределения остатков выполняется.
31. d-критерий Дарбина-Уотсона.
Независимость остатков
проверяется с помощью критерия Дарбина—Уотсона.
Корреляционная зависимость
между текущими уровнями некоторой переменной и уровнями этой же переменной,
сдвинутыми на несколько шагов, называется автокорреляцией.
Автокорреляция случайной
составляющей нарушает одну из предпосылок нормальной линейной модели регрессии.
Наличие (отсутствие) автокорреляции в отклонениях проверяют с помощью критерия Дарбина—Уотсона. Численное значение коэффициента равно
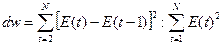
Значение dw статистики близко к величине 2(1 - г(1)), где г(1)
— выборочная автокорреляционная функция остатков первого порядка. Таким
образом, значение статистики Дарбина—Уотсона
распределено в интервале 0—4. Соответственно идеальное значение статистики — 2
(автокорреляция отсутствует). Меньшие значения критерия соответствуют
положительной автокорреляции остатков, большие значения — отрицательной.
Статистика учитывает только автокорреляцию первого порядка. Оценки, получаемые
по критерию, являются не точечными, а интервальными. Верхние (d2) и
нижние (d1)
критические значения, позволяющие принять или отвергнуть гипотезу об отсутствии
автокорреляции, зависят от количества уровней динамического ряда и числа независимых
переменных модели. Значения этих границ для уровня значимости α = 0,05 даны в специальных таблицах. При сравнении
расчетного значения dw статистики с табличным
могут возникнуть такие ситуации: d2 < dw < 2 — ряд остатков не
коррелирован; dw < d} —
остатки содержат автокорреляцию;
d1 < dw < d2 —
область неопределенности, когда нет оснований ни принять, ни отвергнуть
гипотезу о существовании автокорреляции. Если d превышает 2, то это
свидетельствует о наличии отрицательной корреляции. Перед сравнением с табличными
значениями dw критерий следует преобразовать по формуле dw' = 4 – dw.
Установив наличие
автокорреляции остатков, переходят к улучшению модели. Если же ситуация
оказалась неопределенной (d1 < dw< d2 ) применяют другие
критерии. В частности, можно воспользоваться первым коэффициентом
автокорреляции
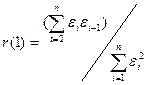
Для принятия решения о
наличии или отсутствии автокорреляции в исследуемом ряду фактическое значение
коэффициента автокорреляции r(1) сопоставляется с табличным (критическим) значением для 5%-ного
уровня значимости (вероятности допустить ошибку при принятии нулевой гипотезы
о независимости уровней ряда). Если фактическое значение коэффициента автокорреляции
меньше табличного, то гипотеза об отсутствии автокорреляции в ряду может быть
принята, а если фактическое значение больше табличного — делают вывод о наличии
автокорреляции в ряду динамики.
32.
Классификация эконометрических моделей.
Можно выделить три основных класса моделей, которые
применяются для анализа и прогнозирования эконометрических систем:
– модели временных рядов
– регрессионные модели с одним уравнением
– системы одновременных уравнений.
Эконометрические
модели делятся на линейные и нелинейные.
33. Система
независимых уравнений, нахождение к-тов модели.
Система независимых уравнений – каждая зависимая переменная (у) рассматривается как
функция одного и того же набора факторов (х):
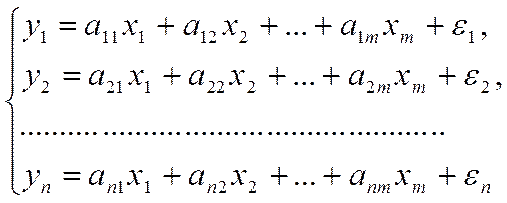
Каждое
уравнение системы независимых уравнений может рассматриваться самостоятельно
как уравнение регрессии. В него м.б. введен свободный член, и к-ты регрессии м.б. найдены МНК.
34. Система рекурсивных уравнений,
определение к-тов модели.
Системы
рекурсивных уравнения используются в
случае если, зависимая переменная у одного из уравнения системы независимых
уравнений выступает в виде фактора х в другом
уравнении этой системы. Система рекурсивных уравнений имеет вид:
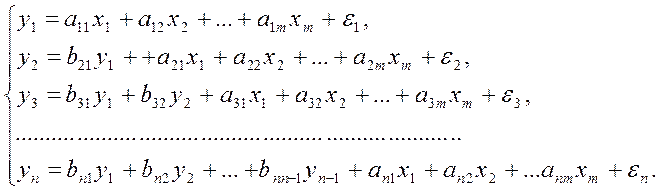
В
данной системе зависимая переменная у включается в каждое последующее уравнение
в качестве факторов все зависимые переменные предшествующих уравнений наряду с
набором собственно фактора х. Каждое уравнение этой системы можно рассматривать
самостоятельно, и его параметры определяются МНК.
35.
Система независимых уравнений, определение идентифицируемости.
Для существования
однозначного соответствия между параметрами структурной и приведенной формами
необходимо выполнение условия
идентификации.
Структурные формы модели могут быть:
• идентифицируемые;
• неидентифицируемые;
• сверхидентифицируемые.
Для того чтобы СФМ была идентифицируема, необходимо,
чтобы каждое уравнение системы было идентифицируемо. В этом случае число параметров СФМ равно числу параметров приведенной
формы. Если хотя бы одно уравнение СФМ
неидентифицируемо, то вся модель считается неидентифицируемой. В этом
случае число коэффициентов приведенной формы модели меньше, чем число
коэффициентов СФМ. Т.о. каждое структурное уравнение д.б. проверено на
идентифицируемость. Идентификация одного уравнения зависит не столько от самого
уравнения, сколько от вида структурных уравнений модели. Идентифицируемость
структурных уравнений означает, что путем линейной комбинации некоторых или
всех уравнений модели невозможно получить ни одного уравнения,, которое бы
противоречило модели и параметры которого отличались бы от параметров
структурных уравнений, подлежащих оценке. Если эконометрическая модель не
идентифицируема. То нельзя оценить параметры модели. В этом случае необходима
новая формулировка всей модели или отдельных ее уравнений.
Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных
коэффициентов. В этом случае можно получить два и более значений одного
структурного коэффициента на основе коэффициентов приведенной формы модели. В сверхидентифицируемой модели хотя бы одно
уравнение сверхидентифицируемо, а остальные уравнения идентифицируемы.
Если обозначить число
эндогенных переменных в i-м уравнении СФМ через H, а
число предопределенных переменных, которые содержатся в системе, но не входят в
данное уравнение, через D то условие
идентифицируемости модели может быть записано в виде следующего счетного правила:
• если D+ 1 < Н уравнение
неидентифицируемо;
• если D+ 1 = Н уравнение
идентифицируемо;
• если D+ 1 >
Н уравнение
сверхидентифицируемо.
Счетное правило является
необходимым, но не достаточным
условием идентификации.
Кроме этого правила для идентифицируемости уравнения должно выполняться дополнительное условие.
Отметим в системе эндогенные
и экзогенные переменные, отсутствующие в рассматриваемом уравнении, но
присутствующие в системе. Из коэффициентов при этих переменных в других уравнениях составим матрицу.
При этом если переменная стоит в левой части
уравнения, то коэффициент надо брать с обратным знаком. Если определитель
полученной матрицы не равен нулю, а ранг не меньше, чем количество эндогенных
переменных в системе без одного, то достаточное условие идентификации для данного уравнения выполнено.
36.
Необходимые и достаточные условия идентификации системы функциональных моделей.
Для существования
однозначного соответствия между параметрами структурной и приведенной формами
необходимо выполнение условия
идентификации.
Структурные формы модели могут быть:
• идентифицируемые;
• неидентифицируемые;
• сверхидентифицируемые.
Для того чтобы СФМ была идентифицируема, необходимо,
чтобы каждое уравнение системы было идентифицируемо. В этом случае число параметров СФМ равно числу параметров приведенной
формы. Если хотя бы одно уравнение СФМ
неидентифицируемо, то вся модель считается неидентифицируемой. В этом
случае число коэффициентов приведенной формы модели меньше, чем число
коэффициентов СФМ. Т.о. каждое структурное уравнение д.б. проверено на
идентифицируемость. Идентификация одного уравнения зависит не столько от самого
уравнения, сколько от вида структурных уравнений модели. Идентифицируемость
структурных уравнений означает, что путем линейной комбинации некоторых или
всех уравнений модели невозможно получить ни одного уравнения,, которое бы
противоречило модели и параметры которого отличались бы от параметров
структурных уравнений, подлежащих оценке. Если эконометрическая модель не
идентифицируема. То нельзя оценить параметры модели. В этом случае необходима
новая формулировка всей модели или отдельных ее уравнений.
Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных
коэффициентов. В этом случае можно получить два и более значений одного
структурного коэффициента на основе коэффициентов приведенной формы модели. В сверхидентифицируемой модели хотя бы одно
уравнение сверхидентифицируемо, а остальные уравнения идентифицируемы.
Если обозначить число
эндогенных переменных в i-м уравнении СФМ через H, а
число предопределенных переменных, которые содержатся в системе, но не входят в
данное уравнение, через D то условие
идентифицируемости модели может быть записано в виде следующего счетного правила:
• если D+ 1 < Н уравнение
неидентифицируемо;
• если D+ 1 = Н уравнение
идентифицируемо;
• если D+ 1 >
Н уравнение
сверхидентифицируемо.
Счетное правило является
необходимым, но не достаточным
условием идентификации.
Кроме этого правила для идентифицируемости уравнения должно выполняться дополнительное условие.
Отметим в системе эндогенные
и экзогенные переменные, отсутствующие в рассматриваемом уравнении, но
присутствующие в системе. Из коэффициентов при этих переменных в других уравнениях составим матрицу.
При этом если переменная стоит в левой части
уравнения, то коэффициент надо брать с обратным знаком. Если определитель
полученной матрицы не равен нулю, а ранг не меньше, чем количество эндогенных
переменных в системе без одного, то достаточное условие идентификации для данного уравнения выполнено.
37.
Оценивание к-тов структурной модели косвенным МНК.
КМНК
прим-ся в случае точно идентифицир-й
структур-ой модели. Этапы примен-я:
1. По структур-й форме модели
формальным образом выписывается приведенная форма модели.
2. Для каждого урав-я привед-й формы модели обычным МНК оцен-ся
приведенный коэф-ты.
3. Коэф-ты прив-ой формы модели транс-ся в параметры структурной модели.
Пример:
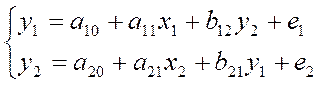
Приведенная
форма модели составит:
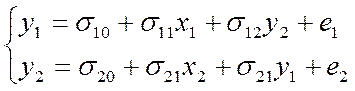
Где
u1, u2 – случ-е ошибки приведенной формы модели
Из 2-го уравнения выведем значение х2 через
остальные переменные: 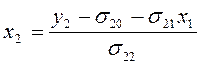
Подставляем в первое уравнение ПФМ: 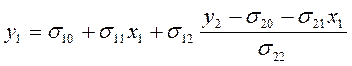
И приводим подобные слагаемые.
Потом также из первого уравнения выражаем значение х1
через у1 и х2.
39.
Назначение и сущность кластерного анализа.
Кластерный
анализ — это совокупность методов, позволяющих
классифицировать многомерные наблюдения, каждое из которых описывается набором
признаков (параметров) Х{9
Х2,..., Л^. Целью
кластерного анализа является образование групп схожих между собой
объектов, которые принято называть кластерами
(класс, таксон, сгущение).
Кластерный анализ — одно из направлений статистического исследования.
Особо важное место он занимает в тех отраслях науки, которые связаны с
изучением массовых явлений и процессов. Необходимость развития методов
кластерного анализа и их использования продиктована тем, что они помогают
построить научно обоснованные классификации, выявить внутренние связи между
единицами наблюдаемой совокупности. Кроме того, методы кластерного анализа
могут использоваться в целях сжатия информации, что является важным фактором в
условиях постоянного увеличения и усложнения потоков статистических данных.
Методы кластерного анализа позволяют решать следующие
задачи [2]:
•
проведение
классификации объектов с учетом признаков, отражающих сущность, природу
объектов. Решение такой задачи, как правило, приводит к углублению знаний о
совокупности классифицируемых объектов;
•
проверка
выдвигаемых предположений о наличии некоторой структуры в изучаемой совокупности
объектов, т.е. поиск существующей структуры;
• построение новых классификаций для слабоизученных явлений,
когда необходимо установить наличие связей внутри совокупности и попытаться
привнести в нее структуру.
40. Дискриминантный анализ, постановка задачи.
Дискриминантный
анализ является разделом многомерного
статистического анализа, который включает в себя методы классификации
многомерных наблюдений по принципу максимального сходства при наличии
обучающих признаков.
Напомним, что в кластерном анализе рассматриваются
методы многомерной классификации без обучения. В дискрими-нантном
анализе новые кластеры не образуются, а формулируется правило, по которому
объекты подмножества подлежащего классификации относятся к одному из уже
существующих (обучающих) подмножеств (классов), на основе сравнения величины дискриминантной функции классифицируемого объекта, рассчитанной
по дискриминантным переменным, с некоторой константой
дискриминации.
Предположим, что существуют две или более совокупности
(группы) и что мы располагаем множеством выборочных наблюдений над ними.
Основная задача дискриминантного анализа состоит в
построении с помощью этих выборочных наблюдений правила, позволяющего отнести
новое наблюдение к одной из совокупностей.
Постановка задачи дискриминантного анализа. Пусть имеется множество М единиц
N объектов наблюдения, каждая i-я единица которого описывается совокупностью р значений дискриминантных
переменных (признаков) хij, (i=1,2,...,
N; j = 1,2,..., р). Причем все множество М объектов включает q обучающих подмножеств (q≥ 2) Mk размером nk каждое и подмножество M0 объектов
подлежащих дискриминации (под дискриминацией понимается различие). Здесь k – номер подмножества (класса), k = 1,2,..., q.
Требуется установить правило (линейную или нелинейную дискриминантную функцию f(X)) распределения m-объектов подмножества M0 по
подмножествам Mk.
Наиболее часто используется линейная форма дискриминантной функции, которая представляется в виде
скалярного произведения векторов А=(а1,а2,...,аp дискриминантных множителей и вектора Хi=(хi1,хi2,…,хip) дискриминантных переменных:
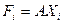
или 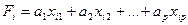
Здесь Xi – транспонированный вектор дискриминантных
переменных; хij — значений j-х признаков у i-го объекта наблюдения.
41.Компонентный
анализ и метод главных компонент. Сущность и назначение методов.
Компонентный анализ является методом
определения структурной зависимости между
случайными переменными. В результате
его использования получается сжатое описание малого объема, несущее почти всю информацию, содержащуюся
в исходных данных. Главные компоненты получаются из исходных переменных путем целенаправленного вращения, т.е.
как линейные комбинации исходных
переменных. Вращение производится
таким образом, чтобы главные компоненты были ортогональны и имели максимальную дисперсию среди возможных
линейных комбинаций исходных
переменных X. При этом переменные
не коррелированы между собой и упорядочены по убыванию дисперсии (первая
компонента имеет наибольшую дисперсию). Кроме того, общая дисперсия после
преобразования остается без изменений.
Метод главных компонент позволяет уменьшить высокую мультиколлениарность объясняющих переменных х. Суть м-да – сократить число объясняющих переменных до наиболее
существенно влияющих факторов. Это достигается путем линейного преобразования
всех объясняющих переменных в новые переменные, так называемые главные
компоненты. Однако этот м-д обладает недостатками:
– главным компонентам трудно подбирать экономический
смысл, что затрудняет экономическую интерпретацию оценок параметров уравнения
регрессии;
– оценки параметров в уравнении получены не по
исходным переменным, а по главным компонентам.
Этот м-д применяется в
основном для оценки значения регрессии и для определения прогнозных значений
результирующей переменной.