Содержание
Задание
1. 3
Задание 2. 4
Задание 3. 5
Задание 4. 7
Задание 5. 10
Задание 6. 13
Список
использованной литературы.. 19
ВАРИАНТ 6
Задание
1
Охотник стреляет три раза по удаляющейся цели. Вероятность
попадания в цель в начале стрельбы равна 0,9, а после каждого выстрела
уменьшается на 0,1. Найти вероятность того, что охотник попадет:
а) только один раз;
b) два
раза;
с) не менее двух раз;
d) хотя
бы один раз;
e)
все три раза или все три раза промахнется.
Решение:
p1=0,9; p2=0,8; p3=0,7
Соответственно:
q1=0,1;
q2=0,2; q3=0,3
k –
число попаданий
а) только один раз:
Р(k=1)=0,9*0,2*0,3+0,1*0,8*0,3+0,1*0,2*0,7=0,092
b) два раза:
Р(k=2)=0,9*0,8*0,3+0,1*0,8*0,7+0,9*0,2*0,7=0,398
с) не менее двух раз:
Р(k>=2)=
Р(к=2)+Р(к=3)= 0,398+0,9*0,8*0,7=0,902
d) хотя бы один раз:
Р(k>=1)=1-
Р(к=0)=1-0,1*0,2*0,3=0,994
е) все три раза или все три раза
промахнется:
Р(k=3
или k=0)=1- Р(k=1)- Р(k=2)=1-0,092-0,398=0,51
Задание
2
Магазин
торгует телевизорами двух марок А и В, пользующихся одинаковым спросом
населения. За день торговли из имеющихся 4 телевизоров марки А и 6 телевизоров
марки В было продано два телевизора. На следующий день магазин получил 6
телевизоров А и 4 телевизора марки В. За второй день торговли продали три
телевизора.
1.
Определить вероятность того, что по крайней мере один
из проданных во второй день телевизоров – марки А.
2.
Проданные во второй день – телевизоры марки А.
Телевизоры каких марок вероятнее всего были проданы в первый день торговли?
Решение:
Вероятность продажи телевизора марки
А в первый день:
Р1А=4/10
Тогда, вероятность после продажи
двух телевизоров в первый день станет равной:
Р2А=4/10-4/10*4/10=6/25
Во второй день поступило 6
телевизоров А и 4 телевизора марки В, т.е. всего телевизоров стало 10-2+6+4=18.
Значит, вероятность увеличилась на 6/18:
Р3А=6/25+6/18=43/75
Это вероятность продажи
телевизора А во второй день.
1. Вероятность того, что по крайней мере один из проданных
во второй день телевизоров – марки А:
P(k>=1)=1-P(k=0)=1-C30*(43/75)0*(32/75)3=0,922
2. Т.к. во второй день все проданные телевизоры марки А, то
вероятность продажи телевизора А во второй день была высока, значит в первый
день вероятнее всего телевизоры А не были проданы, т.е. проданы телевизоры
марки В.
Задание
3
В среднем 20% пакетов акций на аукционе продаются по
первоначально заявленной цене.
1. Какова
вероятность того, что из 5 наугад взятых пакетов акций будет продано по другой
(не первоначально заявленной) цене:
а) ровно 3;
b)
не менее 3;
с) не более 3;
d)хотя
бы один пакет акций?
2. Вычислить
вероятность того, что из ста выставленных на аукционе пакетов акций по
первоначально заявленной цене будет продано:
а) 18;
b) не
менее 18;
с) не более 23;
d) не
менее 15, но не более 25 пакетов акций.
Решение:
р=1-0,2=0,8 – вероятность того, что пакет акций будет продан
по другой цене
1.
n=5 – число
выбранных пакетов акций
k – число пакетов акций, проданных по
другой цене
Используя формулу Бернулли Pn(k)=Ckn*pk*qn-k рассчитаем
вероятности:
а) Р(k=3)= C53*0,83*0,22=0,2048
b) Р(k>=3)= Р(k=3)+
Р(k=4)+ Р(k=5)=0,2048+C54*0,84*0,21+
C55*0,85*0,20=
0,94208
с) Р(k<=3)=1- Р(k>=3)+ Р(k=3)=1-0,94208+0,2048=0,26272
d) P(k>=1)=1-
P(k=0)=1- C50*0,80*0,25=0,99968
2. .
n=100– число выбранных
пакетов акций
p=0,2
вероятность того, что пакет акций будет продан по первоначально заявленной цене
k – число пакетов акций, проданных по
первоначально заявленной цене
a) Р(k=18)=
C10018*0,218*0,882=0,7468
b)
Р(k≥18)=Р(18,100)
Воспользуемся интегральной теоремой Лапласа:
P(k1, k2)=Ф(x2)-Ф(x1)
где Ф(x) - функция Лапласа[1]
x1=(k1-n*p)/√npq=(18-100*0,2)/√100*0,2*0,8=
-0,5
x2=(k2-n*p)/√npq=(100-100*0,2)/√
100*0,2*0,8=20
Ф(-0,5)= -0,1915
Ф(20)= 0,5
Значит, искомая вероятность равна:
P(18,100)=0,5+0,1915=0,6915
c) Р(k≤23)=Р(0,23)
P(k1, k2)=Ф(x2)-Ф(x1)
x1=(k1-n*p)/√npq=(0-100*0,2)/√100*0,2*0,8=
-5
x2=(k2-n*p)/√npq=(23-100*0,2)/√
100*0,2*0,8=0,75
Ф(-5)= -0,5
Ф(0,75)=0,2734
Значит, искомая вероятность равна:
P(0,23)=0,2734+0,5=0,7734
d) Р(15≤k≤25)=P(15, 25)
P(k1, k2)=Ф(x2)-Ф(x1)
x1=(k1-n*p)/√npq=(15-100*0,2)/√100*0,2*0,8=
-1,25
x2=(k2-n*p)/√npq=(25-100*0,2)/√
100*0,2*0,8=1,25
Ф(-1,25)= -0,3944
Ф(1,25)=0,3944
Значит, искомая вероятность равна:
P(15, 25)=0,3944+0,3944=0,7888
Задание
4
В партии из 10 изделий содержится 3 бракованных. Для
проверки качества изделий контролер из всей партии наугад выбирает одновременно
три изделия. Рассматривается случайная величина (с.в.) ξ – число бракованных
изделий, содержащихся в выборке.
1. Составить ряд распределения с.в. ξ и представить его
графически.
2. Найти функцию распределения с.в. ξ и построить его
график.
3. Вычислить математическое ожидание (среднее значение) М
ξ, дисперсию D
ξ и среднее квадратическое (стандартное) отклонение σ (ξ).
4. Определите вероятности:
а) Р {ξ < М ξ };
b) Р
{ξ < М ξ +1};
c) Р
{|ξ - М ξ| < σ (ξ)}.
Решение:
1. n=3 – число выбранных изделий
k – число бракованных изделий среди
выбранных
p=3/10=0,3
– вероятность попадания бракованного изделия
q=7/10=0,7
– вероятность попадания исправного изделия
Р (k=0)
= C30*(0,3)0*(0,7)3=0,343
Р (k=1)
= C31*(0,3)1*(0,7)2=0,441
Р (k=2)
= C32*(0,3)2*(0,7)1=0,189
Р (k=3)
= C33*(0,3)3*(0,7)0=0,027
Ряд распределения с.в. ξ:
|
ξ
|
Р
|
|
0
|
0,343
|
|
1
|
0,441
|
|
2
|
0,189
|
|
3
|
0,027
|
|
|
1
|
и его графическое представление:
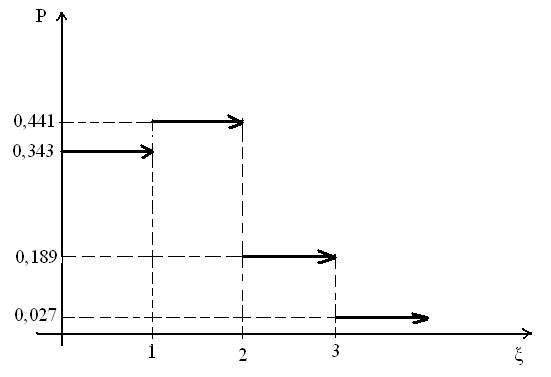
2. Функция распределения с.в.
ξ:
F(x)=P(X-x)
|
F(x)
|
x
|
|
0
|
x<=0
|
|
0,343
|
0<x<=1
|
|
0,784
|
1<x<=2
|
|
0,973
|
2<x<=3
|
|
1
|
x>3
|
Его графическое представление:
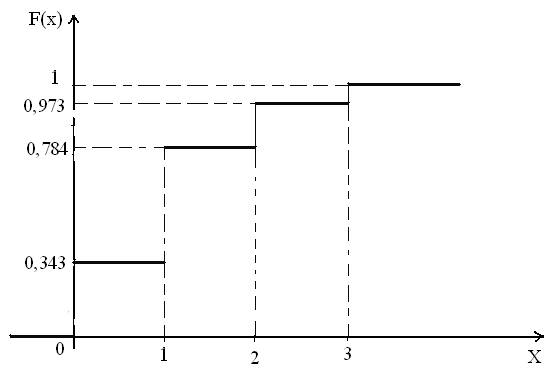
3.
|
ξ
|
Р
|
ξ *Р
|
ξ2
|
ξ2* Р
|
|
0
|
0,343
|
0
|
0
|
0
|
|
1
|
0,441
|
0,441
|
1
|
0,441
|
|
2
|
0,189
|
0,378
|
4
|
0,756
|
|
3
|
0,027
|
0,081
|
9
|
0,243
|
|
Сумма:
|
1
|
0,9
|
-
|
1,44
|
Математическое ожидание (среднее значение):
М ξ=∑ξ *Р=0,9
Дисперсия:
D
ξ= М (ξ2) – (М ξ)2=∑ ξ2* Р - (М ξ)2=1,44-0,92=0,63
Среднее квадратическое (стандартное отклонение):
σ(ξ)=√Dξ=√0,63=0,7
4. а) Р {ξ < М ξ }= Р
{ξ < 0,9}= Р (ξ =0)= 0,343
b) Р
{ξ < М ξ +1}= Р {ξ < 1,9}= Р (ξ =0)+ Р (ξ =1)=
=0,343+0,441=0,784
c) Р
{|ξ - М ξ| < σ (ξ)}= Р {|ξ – 0,9| < 0,7}= Р
(ξ =1)= 0,441
Задание
5
Время ξ (в мин.) между прибытием двух автомашин к
светофору является случайным с плотностью распределения:
p(x)=
c*e-x/2, если x>=0
0, если x<0
1. Установить неизвестную постоянную
С и построить график функции p(x).
2. Найти функцию распределения с.в.
ξ и построить ее график.
3. Вычислить математическое ожидание
(среднее значение) М ξ, дисперсию D ξ и среднее квадратическое
(стандартное) отклонение σ (ξ).
4. Во сколько раз число прибывших к
светофору автомашин со временами между прибытиями больше среднего превосходит
число автомашин со временами между прибытиями меньше среднего?
Решение:
1. Для определения коэффициента С
воспользуемся формулой:
-∞+∞∫f(x)dx=1
Так как f(x) на разных интервалах задана различными выражениями, то
интеграл -∞+∞∫f(x)dx
разбиваем на два интервала:
-∞+∞∫f(x)dx=-∞0∫0dx+0+∞∫С*e-x/2dx=1
Отсюда 0+∞∫С*e-x/2dx=1
-2*С* e-x/2│0+∞=1
2*С=1
Следовательно: С=1/2
В силу этого плотность
вероятности запишется:
p(x)= e-x/2/2, если x>=0
0, если x<0
2. Чтобы найти функцию распределения
с.в. ξ используем формулу:
F(x)= -∞x∫f(x)dx
Если x<=0, то f(x)=0, следовательно,
F(x)= -∞x∫0dx=0
Если x>0, то
F(x)= -∞0∫0dx + 0x∫ e-x/2/2
dx= 0x∫e-x/2/2
dx= -e-x/2│0x=1- e-x/2
Итак:
F(x)= 1- e-x/2, если x>=0
0, если x<0
3. Воспользуемся формулами:
M(X)= -∞+∞∫x*f(x) dx и D(X)= -∞+∞∫x2*f(x) dx – [M(X)]2;
M(X)= -∞+∞∫x*f(x) dx=-∞0∫0dx+0+∞∫x*e-x/2 /2dx= -x*e-x/2 -2*e-x/12│0+∞=2
D(X)= -∞+∞∫x2*f(x) dx – 22=-∞0∫x2*0dx+0+∞∫x2*e-x/2 /2dx-22=
-x2*e-x/17 -4x*e-x/17 - 8e-x/17│0+∞-22=8-22=4
Cреднее квадратическое (стандартное) отклонение σ (ξ):
σ
(x)= √D(X)=2
4. Вероятность того, что число
прибывших к светофору автомашин со временами между прибытиями меньше среднего:
р(x<17)= -∞2∫f(x)dx=02∫ e-x/2/2
dx =-e-x/2│02=1-е-1
и больше среднего:
р(x>17)= 2∞∫f(x)dx=2∞∫ e-x/2/2
dx = -e-x/2│2∞= е-1
Значит, число прибывших к светофору
автомашин со временами между прибытиями меньше среднего превосходит число
автомашин со временами между прибытиями больше среднего в:
р(x<17)/ р(x>17)=
(1-е-1)/ е-1=е-1=1,71828 раз
Задание
6
При измерении веса 25 упаковок
сильнодействующего лекарственного препарата были обнаружены следующие
отклонения (в гр.) от указанного на обертке:
-24.34, -14.59, -18.27, -8.94, -15.09, -10.94,
4.47, 3.05, -8.33, -22.98, 1.75, -32.07, -7.43, -18.63, -12.97, -11.08, -7.44,
-1.70, 6.34, -11.08, -11.12, -15.90, -10.26, -8.07, -6.48.
Необходимо:
1. Определить
исследуемый признак и его тип (дискретный или непрерывный).
2. В зависимости
от типа признака построить полигон или гистограмму относительных частот.
3. На основе
визуального анализа полигона (гистограммы) сформулировать гипотезу о законе
распределения признака.
4. Вычислить
выборочные характеристики изучаемого признака: среднее, дисперсию, среднее
квадратическое (стандартное) отклонение.
5. Используя
критерий согласия «хи-квадрат» Пирсона, проверить соответствие выборочных
данных выдвинутому в п.3 закону распределения при уровне значимости 0,05.
6. Для
генеральной средней и дисперсии построить доверительные интервалы,
соответствующие доверительной вероятности 0,95.
7. С надежностью
0,95 проверить гипотезу о равенстве:
а) генеральной
средней значению -10;
б) генеральной
дисперсии значению 100.
Решение:
1. Тип исследуемого признака непрерывный, т.к. все значения
встречаются ровно по одному разу и распределены в интервале от -32.07 до 6.34 гр.
2. Т.к. тип признака непрерывный, то весь интервал, в
котором заключены все наблюдаемые значения признака разобьем на ряд частичных
интервалов длины h=5 и
найдем mi – сумму частот вариант, попавших в i-й интервал:
|
Номер интервала
|
Частичный
интервал
|
Частоты
|
Относительные
частоты
|
Плотности относительных частот
|
|
i
|
xi-1 - xi
|
mi
|
wi= mi /∑mi
|
wi/h
|
|
1
|
< -25
|
1
|
0,04
|
0,008
|
|
2
|
-25 - -20
|
2
|
0,08
|
0,016
|
|
3
|
-20 - -15
|
4
|
0,16
|
0,032
|
|
4
|
-15 - -10
|
7
|
0,28
|
0,056
|
|
5
|
-10 - -5
|
6
|
0,24
|
0,048
|
|
6
|
-5 - 0
|
1
|
0,04
|
0,008
|
|
7
|
0 - 5
|
3
|
0,12
|
0,024
|
|
8
|
>5
|
1
|
0,04
|
0,008
|
|
Сумма:
|
-
|
25
|
1
|
|
Построим гистограмму:

3. На основе
визуального анализа гистограммы можно сделать предположение о нормальном распределении признака, т.е.:
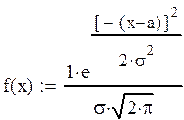
где а –
математическое ожидание, σ
– среднее квадратическое ожидание.
4. Серединные
значения интервалов рассчитаны как xi*= (xi+ xi-1)/2
|
Номер интервала
|
Середины
частичных интервалов
|
Сумма частот
вариант частичного интервала
|
xi**mi
|
xi* 2
|
xi* 2* mi
|
|
i
|
xi*
|
mi
|
|
1
|
-27,5
|
1
|
-27,5
|
756,25
|
756,25
|
|
2
|
-22,5
|
2
|
-45
|
506,25
|
1012,5
|
|
3
|
-17,5
|
4
|
-70
|
306,25
|
1225
|
|
4
|
-12,5
|
7
|
-87,5
|
156,25
|
1093,75
|
|
5
|
-7,5
|
6
|
-45
|
56,25
|
337,5
|
|
6
|
-2,5
|
1
|
-2,5
|
6,25
|
6,25
|
|
7
|
2,5
|
3
|
7,5
|
6,25
|
18,75
|
|
8
|
7,5
|
1
|
7,5
|
56,25
|
56,25
|
|
|
|
25
|
-262,5
|
|
4506,25
|
Вычислим
выборочные характеристики изучаемого признака: среднее значение (MX) , дисперсию, среднее
квадратическое (стандартное) отклонение:
xсрвыб = ∑ xi**mi /n= -262,5/25= -10,5
Dвыб= x*2cp
-xсрвыб 2=∑ xi*2* mi / n - xсрвыб 2=4506,25/25-10,52=70
σвыб=√70=8,366
5. Найдем
исправленную выборочную дисперсию s2:
s2=n/n-1 * Dвыб=25/24 * 70=72,917
и исправленное
выборочное среднее квадратическое отклонение:
s=8,54
Найдем
теоретические частоты mi′:
mi′=n*h/s *φ(ti*)=25*5/8,54*φ(ti*)=14,64*φ(ti*)[2],
где ti*= (xi*- xсрвыб)/s
Составим расчетную таблицу
для нахождения теоретических частот:
|
i
|
xi*
|
ti*= (xi*- xсрвыб)/s
|
φ(ti*)
|
mi′=n*h/s *φ(ti*)
|
|
1
|
-27,5
|
-1,99
|
0,0551
|
0,81
|
|
2
|
-22,5
|
-1,41
|
0,1476
|
2,16
|
|
3
|
-17,5
|
-0,82
|
0,285
|
4,17
|
|
4
|
-12,5
|
-0,23
|
0,3885
|
5,69
|
|
5
|
-7,5
|
0,35
|
0,3752
|
5,49
|
|
6
|
-2,5
|
0,94
|
0,2565
|
3,75
|
|
7
|
2,5
|
1,52
|
0,1257
|
1,84
|
|
8
|
7,5
|
2,11
|
0,0431
|
0,63
|
Затем составим расчетную таблицу для вычисления наблюдаемого
значения критерия χ2набл.:
|
i
|
mi
|
mi′
|
mi - mi′
|
(mi - mi′)2
|
(mi - mi′)2/ mi′
|
|
1
|
1
|
0,81
|
0,19
|
0,04
|
0,05
|
|
2
|
2
|
2,16
|
-0,16
|
0,03
|
0,01
|
|
3
|
4
|
4,17
|
-0,17
|
0,03
|
0,01
|
|
4
|
7
|
5,69
|
1,31
|
1,72
|
0,30
|
|
5
|
6
|
5,49
|
0,51
|
0,26
|
0,05
|
|
6
|
1
|
3,75
|
-2,75
|
7,59
|
2,02
|
|
7
|
3
|
1,84
|
1,16
|
1,35
|
0,73
|
|
8
|
1
|
0,63
|
0,37
|
0,14
|
0,22
|
|
|
|
|
|
χ2набл=3,38
|
По таблице критических точек распределения χ2кр(α,s)[3] при заданном уровне
значимости α=0,05 и числе степеней свободы s=k-3=8-3=5 находим критическую точку правосторонней критической
области:
χ2кр=
χ2кр(0,05;5)=11,1
Так как χ2набл < χ2кр,
то по данным выборки нет оснований отвергать гипотезу о нормальном
распределении признака X
в генеральной совокупности.
6. Т.к. генеральная
совокупность распределена нормально, то для построения доверительного интервала
генеральной средней можно воспользоваться формулой:
xсрвыб - tγ(s/√n)< xсрген< xсрвыб + tγ(s/√n),
где
s - исправленное выборочное среднее квадратическое
отклонение, равное 8,54 (см. п.5);
tγ находят по таблице[4] по заданным n и γ
γ=0,95 (по условию)
t(0.95, 25)=2,064
tγ*(s/√n)=
2,064*8,54/√25=3,53
xсрвыб = -10,5 (см. п.4)
Тогда искомый интервал имеет
вид:
-10,5-3,53< xсрген<-10,5+3,53
-14,03< xсрген<-6,97
Чтобы построить доверительный интервал генеральной дисперсии
сначала найдем доверительный интервал среднего квадратического отклонения по
формуле:
s(1-q) <σген< s(1+q) (при q<1),
0< σген< s(1+q)
(при q>1),
где q
находят по таблице[5]
по данным n и γ
q(0.95, 25)=0,32
Доверительный интервал среднего квадратического отклонения:
8,54*(1-0,32)
<σген<8,54*(1+0,32)
5,807<σген<11,273
Тогда доверительный интервал генеральной дисперсии имеет
вид:
5,8072<Dген<11,2732
33,72<Dген<127,08
7. а) Т.к. доверительный интервал генеральной средней -14,03< xсрген<-6,97 включает
значение -10, то с надежностью 0,95 можно утверждать о правильности гипотезы.
б) Т.к. доверительный интервал генеральной дисперсии
33,72<Dген<127,08
включает значение 100, то с надежностью 0,95 можно утверждать о правильности
гипотезы.
Список использованной литературы
1.
Гмурман В.Е./ Теория вероятностей и математическая
статистика. М.: Высшая школа, 2002
2.
Гмурман В.Е./ Руководство к решению задач по теории
вероятностей и математической статистике. М.: Высшая школа, 2002
3.
Колемаев В.А., Староверов О.В., Турундаевский В.Б./
Теория вероятностей и математическая статистика. М.: Высшая школа, 1991
4.
Семенов А.Т. /Теория вероятностей и математическая
статистика: Учебно-методический комплекс. – Новосибирск: НГАЭиУ, 2003
5.
Семенов А.Т. /Теория вероятностей: Учебное пособие. –
Новосибирск: НГАЭиУ, 2003
[1]
Гмурман В.Е. Руководство к решению задач по теории вероятностей и
математической статистике. М.: Высшая школа, 2002. Прил. 2, С. 390.
[2]
Гмурман В.Е. Руководство к решению задач по теории вероятностей и
математической статистике. М.: Высшая школа, 2002. Прил. 1, С. 388
[3]
Гмурман В.Е. Руководство к решению задач по теории вероятностей и
математической статистике. М.: Высшая школа, 2002. Прил. 5, С. 393.
[4]
Гмурман В.Е. Руководство к решению задач по теории вероятностей и
математической статистике. М.: Высшая школа, 2002. Прил. 3, С. 392.
[5]
Гмурман В.Е. Руководство к решению задач по теории вероятностей и
математической статистике. М.: Высшая школа, 2002. Прил. 4, С. 392.